Méthodes d’analyse statique de pire temps d’exécution de programmes
Les systèmes temps réel
Un système temps réel typique se compose de capteurs, d’un module qui analyse les données reçues par les capteurs et prend une décision, et d’une partie mécanique qui réalise physiquement la décision. Les dernières années ont vu se réaliser l’informatisation croissante du module d’analyse et de prise de décision.
Au niveau d’un tel système informatique, les contraintes d’intégrité se traduisent alors par le fait que tout traitement doit :
- produire des résultats justes ;
- être réalisé dans des délais impartis, sous peine de conséquences graves.
On parle alors de système temps réel dur.
À titre d’exemple et de manière très simplifiée, on peut considérer la commande d’un avion en tant que système constitué d’un manche à balai, d’un capteur de mouvements de ce dernier, de différents capteurs permettant de situer l’avion (en termes de position, d’orientation et de vitesse), d’un système informatique de correction d’erreurs de navigation du pilote, et d’éléments mécaniques réalisant l’action correcte. Dans un tel système informatique, plusieurs tâches sont exécutées, le plus souvent périodiquement (à intervalles réguliers), chaque tâche ayant sa propre période et sa propre priorité. Ainsi, pour chaque capteur, une tâche échantillonne l’intensité relevée. Lorsqu’un mouvement du manche à balai est détecté, une tâche effectue des calculs afin de corriger une erreur éventuelle du pilote (par exemple : un mouvement brusque du manche, une erreur d’appréciation de la situation) et envoie des ordres à des actionneurs. Dans cet exemple, deux contraintes d’intégrité peuvent être mises en évidence :
- Pour chaque tâche considérée de manière isolée, son exécution doit être terminée avant la fin de la période de la tâche ;
- Pour chaque tâche, en tenant compte de l’effet des autres tâches se partageant le même processeur, il faut s’assurer qu’elle puisse toujours s’exécuter selon la période qui lui est attribuée, sans quoi des pertes d’information ou de commande peuvent se produire.
Pour valider la première contrainte, il faut connaître le pire temps d’exécution de la tâche, appelé en anglais WCET (Worst-Case Execution Time). Par la suite, on s’intéressera à l’état actuel des connaissances concernant l’obtention des WCET.
Obtention des pires temps d’exécution
Étant donné un programme P et une architecture sur laquelle il s’exécute, le pire cas d’exécution de P se produit sous l’effet conjugué :
- du programme P lui-même et de son comportement en fonction des données qu’il prend en entrée ;
- d’un certain comportement de l’architecture sur laquelle s’exécute le programme.
Un exemple très simple de programme P permet d’illustrer la première de ces contraintes, la dépendance du temps d’exécution de ce programme aux données qu’il prend en entrée.
1 procedure P (a,b : entier) ; 2 debut 3 pour i depuis 1 jusqu'à a boucle 4 si (b > 4) alors -- Un certain traitement X très long 5 sinon - Un autre traitement Y un peu moins long 6 fin si ; 7 fin boucle; 8 fin procedure P;
Le programme P prend en entrée des valeurs entières a et b, qui ne seront connues qu’au lancement du programme. P comporte une boucle (mot clé « boucle – fin boucle »), qui permet de répéter plusieurs fois l’exécution de portions de code. Dans ce programme, la portion de code des lignes 4 et 5 est répétée un nombre de fois égal à a. Le temps d’exécution du programme dépendra donc de la valeur d’entrée a. De même, P inclut une construction conditionnelle (lignes 4 et 5) permettant d’exécuter un certain traitement si une condition est vérifiée, et un autre traitement dans le cas contraire. Ici, comme la condition testée dépend d’une valeur d’entrée du programme (b), le temps d’exécution du programme dépendra également de cette valeur.
En ce qui concerne l’influence de l’architecture, les processeurs modernes comportent de nombreux dispositifs permettant d’augmenter la rapidité d’exécution des programmes. L’un de ces dispositifs est par exemple le mécanisme de pipeline. Un autre concerne les mémoires cache. Ces dispositifs améliorent les performances générales d’un système informatique. Les travaux concernant l’analyse de WCET portent entre autres sur la prise en compte de ces éléments architecturaux dans l’analyse, en vue de réaliser des systèmes temps réel durs moins onéreux et plus performants.
Un programme tel qu’il est exécuté par le processeur est décomposé en instructions élémentaires très simples (mouvements de données, opérations arithmétiques telles que les additions, soustractions, opérations logiques telles que les comparaisons, branchements, opérations flottantes).
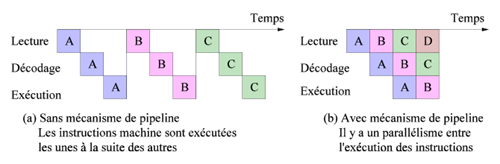
D’un point de vue logique, le processeur donne l’illusion que les instructions sont exécutées les unes après les autres. Mais en réalité, grâce au mécanisme de pipeline, plusieurs instructions sont exécutées « en même temps ». L’exécution d’une instruction est divisée en phases (par exemple, lecture, décodage, exécution). L’unité fonctionnelle dédiée à une phase ne traite qu’une instruction à la fois, mais deux phases différentes de deux instructions peuvent être exécutées en parallèle. La méthode de pipeline ne change pas la durée d’exécution d’une instruction mais augmente le débit (nombre d’instructions exécutées par seconde).
Les informations manipulées par les programmes sont stockées dans la mémoire vive de la machine. Pour diminuer le temps d’accès à cette mémoire, on intercale entre la mémoire et le processeur des mémoires plus rapides mais moins volumineuses que la mémoire vive, qui sont appelées mémoires cache. Le transfert entre mémoire vive et mémoire cache est réalisé automatiquement. On peut comparer une mémoire cache au placard de votre cuisine : il a une beaucoup plus petite contenance que les rayons de l’hypermarché, mais est beaucoup plus rapide d’accès lorsque vous préparez votre déjeuner.
Méthodes d’obtention des pires temps d’exécution
Deux catégories de méthodes peuvent être envisagées pour déterminer le pire temps d’exécution d’un programme.
- La première catégorie, qui comprend les méthodes dites d’analyse dynamique, consiste à exécuter le programme sur une machine en lui fournissant différents jeux d’entrée (valeurs a et b dans le programme P ci-dessus) et à mesurer le temps de chaque exécution. Si le principe des méthodes dynamiques est simple, elle est en revanche difficile à mettre en œuvre. En effet, la connaissance précise du programme est nécessaire pour générer des jeux d’entrée valides qui peuvent être en nombre très important (pour le programme P exemple, il faut considérer tous les couples de valeurs entières possibles).
- La seconde catégorie regroupe les méthodes d’analyse statique. Le but de ces méthodes est de s’affranchir des tests. Elles fournissent un résultat sans exécuter le programme, simplement en examinant sa structure. Contrairement aux méthodes dynamiques, les méthodes statiques fournissent un WCET estimé supérieur ou égal au WCET réel, ce qui est pessimiste, mais sûr. Cette garantie provient de la modélisation des éléments architecturaux du processeur et de la prise en compte de l’ensemble des chemins d’exécution, sans les énumérer de manière exhaustive. Lorsque le comportement d’un élément ne peut pas être prédit précisément, alors on choisit son comportement le plus pessimiste. Dans la suite, on donne des éléments sur les méthodes d’analyse statique.
Analyse statique de pire temps d’exécution de programmes
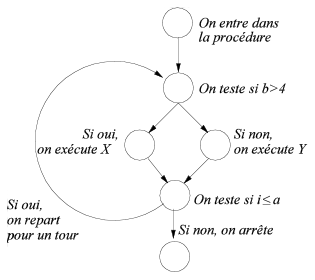
Graphe de flot de contrôle du programme P (donné précédemment en exemple).
La structure de graphe de flot de contrôle décrit dans quel ordre les instructions élémentaires doivent être exécutées par le processeur. Un nœud du graphe, représenté par un rond sur la figure, correspond à une suite d’instructions machine, sans aucune prise de décision, ou instruction de branchement, à l’intérieur. Un arc, c’est à dire une flèche sur la figure, représente les mises en séquence possibles entre les nœuds (un nœud destination d’une flèche s’exécutera toujours après un nœud source de la flèche).
L’analyse statique opère sur une représentation abstraite des programmes, qu’elle transforme en un problème mathématique, dont la résolution produit les pires temps d’exécution. Une des représentations les plus utilisées est la représentation sous forme de graphe de flot de contrôle.
Une analyse du matériel, basée sur un modèle mathématique de l’architecture du processeur, permet d’associer à chaque nœud du graphe de flot de contrôle (suite d’instructions machine) un pire temps d’exécution. Cette partie de l’analyse peut être relativement complexe à réaliser, à cause des éléments améliorateurs de performances présents dans les processeurs modernes.
Il reste ensuite, à partir du temps d’exécution individuel de chaque nœud du graphe, à déterminer le pire temps d’exécution du programme complet. Le calcul du WCET est au final réalisé en utilisant des méthodes de résolution mathématiques. Ainsi, des techniques utilisant l’algorithmique des graphes, ou bien des techniques de programmation linéaire, sont appliquées sur les graphes de flot de contrôle. À ce propos, il faut remarquer que les graphes sont largement utilisés pour modéliser des systèmes physiques comme des réseaux de transports, mais aussi pour modéliser des systèmes abstraits comme l’exécution d’un programme.
Soit n valeurs entières x1, …, xn. Les méthodes de programmation linéaire en nombres entiers permettent de trouver les valeurs des xi telles qu’une fonction linéaire des xi (a1 x1 + a2 x2, … + an xn, où les ai sont des constantes) est maximale, en considérant de surcroît que les xi sont soumis à des contraintes linéaires (par exemple : x1 ≥ 0, x2 > 0, a x5 + d x6 ≤ 10, avec a et d constantes entières).
On montre ici le problème mathématique généré pour l’exemple, en supposant que la boucle est exécutée au maximum 10 fois.

Calcul du WCET par programmation linéaire.
Les xi représentent le nombre d’exécutions des nœuds du graphe, les xi,j représentent le nombre de franchissements des arcs, et les ti les temps d’exécution des nœuds, retournés par l’analyse du matériel. Trouver le temps d’exécution maximal de P revient alors à maximiser l’expression mathématique donnée en haut à droite de la figure.
Conclusion
Dans le domaine des systèmes à contraintes temporelles strictes comportant des processeurs évolués, un éventail de techniques a été proposé afin d’obtenir une estimation à la fois précise et sûre du temps d’exécution de tâches dans le pire cas. Certaines de ces techniques ont donné lieu à la réalisation de logiciels issus aussi bien du milieu académique qu’industriel. À l’heure actuelle, le défi le plus important de ce type de méthodes se pose au niveau matériel : il s’agit de suivre le rythme effréné de complexification de la structure interne des processeurs.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Isabelle Puaut
Professeur à l'Université de Rennes 1, chercheuse dans l'équipe CAPS de l'IRISA.