Routage dans les petits mondes
Le fait que des chemins très courts existent est déjà un phénomène surprenant, mais ce qui l’est davantage encore est qu’il soit possible de les découvrir localement, sans connaissance de l’ensemble du réseau. Des travaux de recherche récents ont permis de mieux comprendre ce dernier point.
1. Origine de l’étude des petits mondes
L’utilisation du terme « petit monde » remonte à l’expérience sociologique de Stanley Milgram effectuée en 1967. Il s’agissait de demander à un échantillon (supposé aléatoire) de 300 Américains du Nebraska de faire parvenir une lettre à un individu cible dont ils n’avaient pas l’adresse, mais sur lequel ils possédaient des informations (sa profession : courtier, son lieu de travail : Boston…). La règle était de ne transmettre la lettre qu’à une de ses connaissances propres.
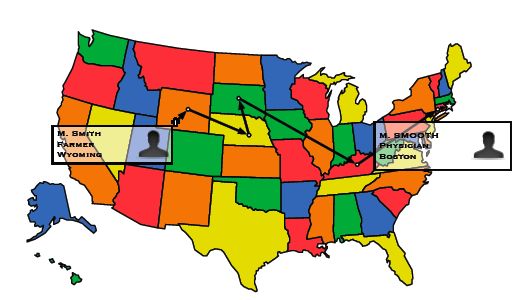
Parcours d’une lettre dans l’expérience de Milgram.
Relativement peu de lettres sont arrivées à destination (environ un quart), mais le résultat surprenant fut que la longueur moyenne d’une chaîne de porteurs du message de son origine jusqu’à sa destination était très faible (environ 6). Pourtant, le nombre d’individus potentiellement concernés par le réseau social mis en jeu était très important (plusieurs centaines de millions), les personnes étaient éloignées géographiquement et socialement entre elles, et enfin, aucune d’elles n’avait la carte du réseau social.
On parle également des « six poignées de main » en référence à cette expérience, pour signifier le fait qu’il serait possible d’atteindre n’importe quel individu par une chaîne de six poignées de mains entre des individus qui se connaissent deux-à-deux. Bien sûr, le chiffre de 6 n’est pas exact : il s’agit d’une moyenne expérimentale. Toutefois, l’ordre de grandeur (logarithmique en fonction de la taille du réseau) semble, lui, pertinent, il a même été vérifié par la suite en reproduisant l’expérience sur des courriers électroniques [1].
Comment fonctionne l’effet « petit monde » ?
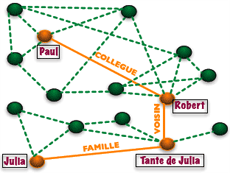
Chemin de longueur trois reliant Julia à Paul.
Le type des liens utilisés est précisé. Les liens en pointillés représentent le reste du réseau social.
En voici un exemple imaginaire dans un réseau social. Supposons que Julia rencontre Paul. Paul lui parle de son emploi de journaliste, qu’il a obtenu grâce à un ami, Robert, qui habite Reuilly-les-Olivettes. Julia s’étonne, car sa tante, qui habite ce village, y connaît un journaliste nommé Robert (son voisin) : « le monde est petit ! »
Nous avons donc le chemin suivant, de longueur 3 :
Julia —lien familial— Tante de Julia —lien de voisinage— Robert —lien professionnel— Paul.
Quoi d’étonnant ? On pourrait trouver l’effet petit monde assez naturel : si un individu a 100 relations (amicales, professionnelles, etc.) et que chaque relation a elle-même 100 relations, on voit qu’en 3 sauts le long des relations, on pourrait atteindre 1003 = 1 million d’individus. Cela expliquerait que tout individu puisse être atteint en peu de sauts.
Toutefois, les réseaux sociaux ont la particularité d’être très cloisonnés, c’est-à-dire que les relations d’un même individu ont de grandes chances de se connaître entre elles. Ainsi, si j’ai 100 amis et que chacun de mes amis a 100 amis, dont 99 sont aussi parmi mes amis, alors en deux sauts on n’atteint plus que 200 personnes au lieu des 10 000 escomptées.
L’effet petit monde n’est donc pas si évident que cela, et il devient d’autant plus mystérieux lorsque l’on s’intéresse au routage qui est exécuté sans carte dans un réseau.
Un routage spécifique aux petits mondes
Le terme de routage désigne l’acheminement d’un message d’un point à un autre dans un réseau.
La spécificité du routage dans les petits mondes tient dans la connaissance partielle que les individus ont du réseau, et dans son efficacité malgré cela. En effet, il est impossible de regarder la carte du réseau pour choisir le chemin le plus court, et chaque individu n’en a qu’une vision locale : celle de ses propres connaissances. Dans ces conditions, comment le routage réussit-il à être aussi rapide ?
Reprenons l’exemple de Julia et Paul. Supposons que Julia n’ait pas encore rencontré Paul, et qu’on lui demande de faire parvenir un message à un dénommé Paul, journaliste à Paris.
Deux cas peuvent se présenter :
- 1er cas : la tante de Julia lui a parlé de son voisin Robert. Comme c’est le seul journaliste de son entourage, Julia pense à transmettre la lettre à sa tante, qui la transmettra à Robert, et le message arrivera en 3 sauts.
- 2e cas : la tante de Julia ne lui a jamais mentionné son voisin Robert. Julia réfléchit à quelle connaissance elle pourrait transmettre le message. Ayant de nombreux amis parisiens, elle choisit de le transmettre à l’un deux. Sa tante postière à Reuilly-les-Olivettes n’est clairement pas une bonne option. Alors, la lettre peut mettre plus de temps à arriver, ou même ne jamais parvenir à destination, si l’un des intermédiaires se décourage. Cela pourrait expliquer l’un des résultats de l’expérience de Milgram (pourquoi les 3/4 des lettres ne sont jamais arrivées).
On voit bien dans cet exemple qu’il existe deux types de connaissances des distances du réseau : une connaissance globale (tout le monde estime a priori qu’un habitant de Reuilly-les-Olivettes est éloigné d’un parisien) et une connaissance locale (la tante de Julia connaît Robert, leur distance est donc 1, et elle peut être la seule à détenir l’information de cette « connexion »).
2. Modélisation du routage dans les petits mondes
C’est à partir de l’observation qu’il existe des distances connues globalement et d’autres localement que Jon Kleinberg a présenté en 2000 le premier modèle mathématique de réseau reproduisant l’effet petit monde [2].
Un modèle de réseau à deux types de liens
Comme il s’agit d’un premier modèle, les hypothèses sur le réseau sont simplifiées : on suppose que les individus sont placés sur une grille régulière qui représente leurs positions géographiques et que cette grille est connue globalement de tous.
Sur cette grille, Kleinberg ajoute un lien sortant en chaque point. Ce lien représente une connaissance locale, personnelle (par exemple amicale) connue de ce point seul. Le lien est orienté, cela signifie que la connaissance entre les deux individus reliés n’est pas forcément mutuelle (par exemple : je connais le roi des Belges, mais le roi des Belges ne me connaît pas). Les liens sont distribués aléatoirement sur la grille (selon une certaine distribution de probabilités). Plus précisément, la probabilité que le lien aléatoire de A pointe vers B est inversement proportionnelle à la distance entre A et B dans la grille, élevée à une certaine puissance s, où s est un exposant supérieur à 0 à paramétrer.
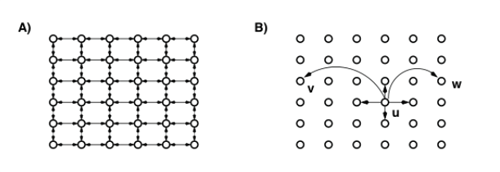
Modèle de Kleinberg avec deux liens sortant par point.>
(A) représente la grille des connaissances globales. (B) représente les contacts du nœud u : 4 connaissances dans la grille et 2 connaissances locales supplémentaires.
Le mode de transmission des messages (c’est-à-dire l’algorithme de routage) proposé est l’algorithme glouton, qui va toujours vers le voisin qui est le plus proche de la destination selon la distance globale (ici, la distance dans la grille) jusqu’à atteindre la cible. Il est important de remarquer que l’on peut choisir d’envoyer le message sur son lien aléatoire, mais les autres points (individus) du réseau n’ont pas connaissance de ce lien. En particulier, A peut avoir un lien aléatoire qui le relie directement à la destination recherchée, mais si B a fait parvenir le message à A, c’est uniquement parce que A était son voisin le plus proche de la destination dans la grille, sans les nouveaux liens aléatoires.
Apparition de l’effet petit monde
Le point le plus surprenant du modèle de Kleinberg est l’effet de seuil observé sur le paramètre s.
Kleinberg démontre en effet que si l’exposant s vaut 2, alors l’effet petit monde apparaît : pour un réseau de n points, l’algorithme glouton parvient à acheminer un message d’un point à n’importe quel autre en Θ(log2 n) sauts avec une forte probabilité. Cela signifie que la longueur des chemins est une fonction polylogarithmique du nombre total de points, sans que l’on ait besoin de la carte du réseau. Pour avoir un ordre d’idée, le logarithme en base 10 de 1 million vaut 6, et celui de 100 000 000 millions vaut 8…
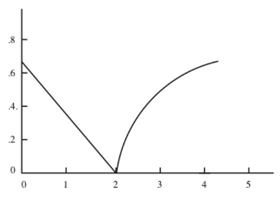
Courbe symbolique de variation de l’exposant α de la longueur moyenne nα d’un chemin glouton dans une grille de côté n (axe vertical) en fonction du paramètre s (axe horizontal) dans le modèle de Kleinberg.
Kleinberg montre aussi que par contre, si l’exposant s est strictement inférieur ou strictement supérieur à 2, alors le nombre de sauts nécessaires à l’algorithme glouton pour parvenir à destination sera toujours au moins polynomial en la taille du réseau (le nombre de points n). Plus précisément : il sera au moins de l’ordre de n(2-s)/3 si 0 ≤ s < 2. Pour se donner un ordre d’idée, on peut observer la différence des valeurs obtenues pour un réseau de cent millions de points. Pour s = 2, la longueur des chemins est de l’ordre de 82 = 64, tandis que pour s = 1, la longueur des chemins est déjà de l’ordre de 108/3 soit environ 468. Et dès que s s’éloigne beaucoup de la valeur 2, la longueur des chemins explose. Par exemple pour s = 10, la longueur d’un chemin calculé par l’algorithme glouton est de l’ordre de n(s-2)/(s-1), soit 106×8/9, c’est-à-dire environ 213 876.
Ce phénomène de seuil tient à la répartition des liens aléatoires sur la grille en fonction de s : lorsque s est trop petit (< 2), la probabilité de pointer sur des points très éloignés est forte. Ainsi, le réseau est rempli de raccourcis qui sautent de grandes distances. On peut alors très vite se rapprocher de la destination, mais une fois proche d’elle, il n’y a pas de raccourcis sur des distances « courtes » qui peuvent nous faire gagner du temps : on « marche » donc le long de la grille et les chemins sont finalement longs. Inversement, lorsque s est trop grand, les liens aléatoires sont trop courts : il y a de nombreux raccourcis sur les petites distances, mais on ne trouve pas de raccourci qui nous permette de faire un grand saut pour se rapprocher d’une destination éloignée. Les chemins sont alors constitués de très nombreux raccourcis et restent ainsi également longs.
Il est important de souligner que si l’algorithme glouton ne calcule pas de chemins courts dans ces cas, cela ne signifie pas pour autant que ces chemins n’existent pas. En particulier, pour 0 ≤ s < 2, le diamètre du réseau est logarithmique : entre toute paire de nœuds, il existe un chemin dont la longueur est de l’ordre de log(n). Pourtant, l’algorithme glouton ne parvient pas à trouver ces chemins. On voit bien ici que l’effet petit monde ne tient pas seulement à la présence de chemins courts mais à une structure particulière qui rend possible leur découverte malgré une vue partielle.
Rappelons que le terme petit monde n’a pas de définition formelle. Dans la littérature, il peut parfois décrire l’existence de chemins courts combinée à une forte densité du voisinage [3], sans tenir compte du routage avec une vue partielle, ce qui n’est pas la définition considérée ici.
Quelle est la structure sous-jacente des petits mondes ?
Le modèle de Kleinberg montre qu’une distance connue globalement en forme de grille, augmentée de relations connues localement, et bien distribuées vis-à-vis de la grille, fait émerger l’effet petit monde. En supposant que les distances connues globalement soient les positions géographiques des individus, la structure de grille régulière ne paraît pas très réaliste. Une question naturelle est alors de chercher à étendre ce modèle : quelle doit être la structure des distances globales vis-à-vis des distances locales en général pour obtenir l’effet petit monde ?
Il a été démontré par la suite [4] que le modèle de Kleinberg peut être généralisé aux grilles de dimension d quelconque avec un effet de seuil similaire : l’exposant s doit être égal à d pour faire émerger l’effet petit monde. En poussant plus loin l’analyse, on constate que la façon dont varie la taille d’un voisinage en fonction de son rayon dans les grilles (de façon polynomiale) est particulièrement adaptée pour répartir les liens supplémentaires sur toutes les échelles de distance. Un article récent [5] démontre alors que l’on peut généraliser le modèle à tous les réseaux qui satisfont cette propriété au sens large, on parle de réseaux à croissance bornée. Pour obtenir l’effet petit monde, la probabilité que le lien supplémentaire du nœud u soit le nœud v à distance k doit être inversement proportionnelle au nombre de nœuds dans un rayon k autour de u. Ainsi, plus la densité d’individus proche de soi est importante, moins on a de chances de connaître une personne éloignée géographiquement, ce qui semble une hypothèse réaliste dans de nombreux contextes. Un autre article [6] a étendu cette généralisation à tous les réseaux pour lesquels il est possible de couvrir tout voisinage de rayon r par un nombre C de voisinages de rayon r/2, C étant une constante. On dit que le réseau est de dimension doublante bornée. De façon encore plus récente, de nouveaux modèles sont apparus : il existe deux nouvelles classes de réseaux que l’on sait augmenter par des liens aléatoires pour faire émerger l’effet petit monde [7, 8].
La question est alors de déterminer à quel point on peut généraliser le modèle de Kleinberg : est-il possible d’ajouter des liens sur n’importe quel type de structure pour obtenir un petit monde, ou bien y a-t-il une structure spécifique nécessaire ? Une réponse à cette question a été donnée récemment [9] en exhibant une famille de réseaux sur lesquels aucune distribution de liens ne peut faire émerger l’effet petit monde. Dans ces réseaux, le nombre de directions possibles pour un lien est très important, et il est impossible de répartir suffisamment bien les liens pour que le routage glouton les utilise efficacement.
La question de savoir quelle doit être la propriété minimale à satisfaire pour la structure des distances globales n’est donc pas close aujourd’hui. Les résultats obtenus nous donnent néanmoins à la fois des indications sur la structure sous-jacente des réseaux réels présentant l’effet petit monde (comme les réseaux sociaux), et des outils pour construire des réseaux informatiques dont on peut garantir la propriété de routage efficace sans connaissance de la carte globale du réseau.
3. Applications aux réseaux de pair à pair
Les travaux de modélisation des réseaux petits mondes peuvent avoir des applications pour le routage dans les réseaux de pair à pair. Dans un réseau de pair à pair, les points sont des ordinateurs, et leurs connexions sont dues à la fois à un logiciel de pair à pair et aux préférences des utilisateurs en terme de choix de fichier à télécharger.
Analogie avec les réseaux sociaux
En particulier, comme c’est le cas dans un réseau social, les communications s’établissent localement, et il n’y a pas de serveur central. Pour ces réseaux, on cherche justement à pouvoir calculer des chemins très courts sous la contrainte que les ordinateurs participant au réseau n’en ont qu’une vue locale et agissent individuellement. On voit qu’il s’agit en quelque sorte de parvenir à reproduire l’effet petit monde sur ces réseaux.
Par ailleurs, les réseaux de pair à pair sont des réseaux virtuels : une connexion directe entre deux ordinateurs dans un réseau de pair à pair peut en réalité correspondre à l’existence d’un chemin de plusieurs sauts dans le réseau Internet. Il ne s’agit donc pas d’un câble mais d’un lien virtuel représentant la possibilité d’une communication connue. On peut donc modifier les réseaux de pair à pair en leur ajoutant des liens sans que cela ne nécessite en réalité d’ajouter un câble physique.
Enfin, il existe un rapprochement entre les grands réseaux sociaux et les grands réseaux d’ordinateurs dans leur construction : les points se sont reliés aux autres individuellement et créent de nouvelles connexions selon des préférences « sociales » (par exemple, selon une préférence en termes de genre de musique dans un réseau de pair à pair d’échange de fichiers musicaux).
Ces caractéristiques font des réseaux de pair à pair un bon terrain d’applications potentielles des modèles mathématiques de réseaux petits mondes. On peut par exemple choisir de construire un réseau virtuel pour le pair à pair selon la grille augmentée de Kleinberg, pour y obtenir un routage décentralisé efficace des fichiers. C’est par exemple le cas du modèle de réseau de pair à pair CHORD.
Un modèle de petit monde pour le pair à pair
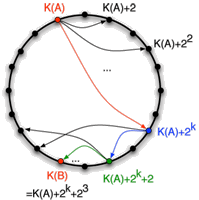
Le principe de CHORD [10] est d’attribuer une clé à chaque fichier et à chaque utilisateur, et d’utiliser un espace structuré pour gérer et retrouver ces clés, tandis que le réseau d’ordinateurs qui échangent ces fichiers n’a, lui, pas de structure prédéfinie. CHORD utilise le modèle de Kleinberg en dimension 1 pour structurer cet espace de clés. L’ensemble des n clés est ainsi réparti sur un anneau (virtuel) et depuis chacun des n nœuds de l’anneau partent log(n) liens vers les nœuds à distance 2, puis 4, puis 8, etc. Cela correspond en réalité à une répartition déterministe des liens du modèle de Kleinberg.
 |
 |
|
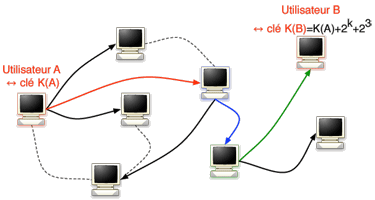
Ordinateurs (et donc utilisateurs) mis en jeu dans le réseau de pair à pair, et anneau CHORD correspondant (schéma simplifié). |
|
En simplifiant le principe, voici un exemple décrivant comment cette utilisation d’un modèle de petit monde permet de retrouver très rapidement un utilisateur dans un réseau décentralisé. Supposons que l’utilisateur A soit à la recherche de l’utilisateur B, car il possède un fichier qu’il recherche. A a besoin de l’adresse IP de cet utilisateur, mais ne connaît que sa clé K(B) dans le réseau CHORD (cette clé seule ne donne pas de route dans le réseau physique d’Internet). A a stocké dans sa mémoire les log(n) nœuds correspondants aux log(n) liens supplémentaires qu’il a sur l’anneau virtuel. Si B est parmi ces nœuds, alors A retrouve directement l’adresse de B. Sinon, A va renvoyer sa requête au nœud dont la clé est la plus proche de K(B) parmi les log(n) nœuds qu’il a mémorisés.
Finalement, il s’agit d’un routage glouton à la Kleinberg, où l’on divise la distance à la cible par deux à chaque pas. Ainsi, sans connaissance globale, A va retrouver l’adresse de B en seulement log(n) étapes, le nombre maximum de fois qu’il faut diviser la distance par deux jusqu’à ce qu’elle soit nulle.
Pour plus de détails sur le fonctionnement des réseaux de pair à pair, on pourra consulter le document Interstices sur ce sujet.
Au-delà de la propriété de petit monde
En recherchant des modèles mathématiques d’une propriété observée dans les graphes réels, l’effet petit monde, les chercheurs ont par la même occasion développé des modèles de réseau très efficaces pour les communications informatiques. Mais l’effet petit monde n’est pas la seule propriété observée sur les réseaux réels. Les réseaux sociaux, les réseaux d’ordinateurs et d’autres grands réseaux d’interaction présentent par exemple une forte densité de voisinage et une distribution du nombre de liens par nœud bien particulière, selon des données expérimentales récentes. En comprenant comment ces propriétés interagissent entre elles, et comment nous pourrions les reproduire par des modèles, on peut espérer dans les prochaines années des avancées à la fois dans la conception de réseaux informatiques efficaces et dans la compréhension des réseaux réels.
- P. S. Dodds, R. Muhamad, D. J. Watts. An experimental study of search in global social networks. Science, vol 301, pages 827-829, 2003.
- J. Kleinberg. The Small-World Phenomenon : An Algorithmic Perspective. In Proceedings of the 32nd ACM Symposium on Theory of Computing (STOC), pages 163–170, 2000.
- D. J. Watts, S. H. Stogatz, Collective dynamics of small world networks, Nature vol. 393, pages 440-442, 1998.
- L. Barrière, P. Fraigniaud, E. Kranakis, D. Krizanc, Efficient routing in networks with long range contacts, In Proceedings of the 15th International Symposium on Distributed Computing (DISC), 2001.
- P. Duchon, N. Hanusse, E. Lebhar, Could any graph be turned into a small world?, Theoretical Computer Science, Volume 335(1), pages 96-103, 2006.
- A. Slivkins, Distance estimation and object location via rings of neighbors, In Proceedings of the 24th Annual ACM Symposium on Principles of Distributed Computing (PODC), pages 41–50, 2005.
- P. Fraigniaud, Greedy routing in tree-decomposed graphs: a new perspective on the small-world phenomenon, In Proceedings of the 13th Annual European Symposium on Algorithms (ESA), pages 791–802, 2005.
- I. Abraham, C. Gavoille, Object location using path separators, In 25th Annual ACM Symposium on Principles of Distributed Computing (PODC), pages 188-197, 2006.
- P. Fraigniaud, E. Lebhar, Z. Lotker, A doubling dimension threshold for augmented grapghs navigability, In Proceedings of 14th Annual European Symposium on Algorithms (ESA), 2006.
- I. Stoica, R. Morris, D. R. Karger, M. F. Kaashoek, and H. Balakrishnan. Chord : A scalable peer-to-peer lookup service for internet applications. In Proc. of the ACM SIGCOMM, pages 149–160, 2001.
en français
- « Que le monde est petit ! » Jean-Paul Delahaye, Pour la Science n° 308 juin 2003
- Un tout petit monde (Small World), roman de David Lodge, traduit de l’anglais, Rivages poche 2004
- RELAIS : une expérience scientifique pour tous, un site où l’on peut tester l’expérience de Milgram avec de vraies lettres
en anglais
- Six degrees, the science of a connected age, Duncan J. Watts, Vintage Edition, 2004
- The Small World Project, un site où l’on peut lancer des chaînes de messages comme dans l’expérience de Milgram
- The Oracle of Bacon at Virginia, un site où l’on peut calculer la distance d’un acteur à l’acteur Kevin Bacon
- Cinema FreeNet, un site où l’on peut demander la distance entre deux acteurs
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Nicolas Schabanel