La modélisation des procédés biologiques de dépollution
Certes, il est très difficile de modéliser le processus de dépollution. D’autant plus difficile que des pressions accrues s’exercent sur la recherche, pour qu’elle obtienne des résultats à court terme.
Pour en avoir une idée, transportons-nous au début d’un XVIIe siècle imaginaire et anachronique, mais terriblement plausible.
La scène se passe dans un laboratoire. Un chercheur fichu comme l’as de pique s’affaire autour d’un dispositif de plans inclinés. Entre un homme en costume-cravate, très sûr de lui :

La Vie de Galilée de Bertold Brecht, mise en scène par Jean-François Sivadier.
Photo © Alain Dugas
– Galilée, passez immédiatement dans mon bureau.
– Oui, Monsieur le Directeur.
La porte se ferme. Quelques minutes plus tard :
– Je vois, Galilée, que vous n’avez pas renoncé à vos satanées expériences sur les plans inclinés. Combien de fois faudra-t-il vous rappeler que nous sommes ici dans un institut d’astronomie ?
– Certes, Monsieur le Directeur, mais… tenez… ma dernière lunette…
– Galilée. Vous êtes notre meilleur élément, nous le savons bien. Votre lunette astronomique est fantastique, elle nous a valu les honneurs. Mais comprenez-moi bien, vous êtes ici pour faire de l’astronomie, ce temps que vous perdez à faire rouler des billes, vous le volez au contribuable qui vous paie.
– Que Monsieur le Directeur ne se mette pas en colère, mais qu’il considère plutôt que je m’en vais comprendre que l’inertie est un phénomène universel, valable sur la terre comme au ciel… et que par conséquent, en aucune façon je ne vole la nation…
– Il suffit ! Galilée, nous savons que les Japonais préparent une lunette en grand secret. Vous devez améliorer la vôtre, je veux une lunette deux fois plus performante dans trois mois. Nous n’avons pas de temps à perdre.
Et le chercheur de sortir le dos courbé, et le regard las. Et c’est ainsi que les lois de la mécanique ne furent pas inventées dans un tel monde à jamais figé au XVIIe siècle de la pensée.
Cette fable, c’est notre actualité de chercheurs. Le directeur symbolise ce qu’il est convenu d’appeler la « demande sociale », qui promeut une vision utilitariste de la recherche. Or dans le domaine qui est le nôtre, la modélisation de procédés de dépollution, dont le but est pourtant bien d’aider la société, cette vision ne permet pas d’avancer très loin.
Que cherchons-nous à modéliser ?
La modélisation d’un phénomène consiste à le réduire aux lois mathématiques qui en rendent compte, par exemple la conservation de la masse, la loi de la gravitation, la loi des gaz parfaits. Ces lois se traduisent en équations qui autrefois étaient « résolues » à la main et maintenant le sont grâce à des ordinateurs de plus en plus puissants. C’est par exemple ce qui est fait dans les modèles physico-chimiques du réchauffement climatique. Mais il y a d’énormes difficultés à faire entrer dans les modèles les composantes biologiques d’un problème. C’est que, dans la plupart des cas, les « équations du vivant » ne sont pas connues. Et c’est en grande partie le cas dans le traitement biologique des eaux usées.
Les eaux usées contiennent en quantités parfois très importantes des éléments chimiques produits par l’activité humaine, comme les phosphates et les nitrates. Rejetés dans la nature, ils sont considérés comme nuisibles, mais constituent une nourriture de choix pour les micro-organismes qui se développent alors de façon excessive dans les lacs, les rivières, les bordures des mers, au détriment de formes de vie plus complexes qui peuvent avoir un intérêt économique important. Le principe de la dépollution biologique est simple. Il consiste à faire comme la nature, mais de façon contrôlée, c’est-à-dire à faire croître les micro-organismes indésirables dans un espace confiné, comme le bassin d’une station d’épuration.
La modélisation d’un procédé de dépollution biologique repose donc essentiellement sur les lois de croissance des micro-organismes. Que savons-nous à ce sujet ?
De la croissance des populations de micro-organismes…
Les micro-organismes unicellulaires consomment des espèces chimiques dont ils tirent l’énergie (éventuellement avec l’aide de la lumière dans le mécanisme de la photosynthèse) et la matière nécessaires à leur croissance, qui se termine par une division cellulaire. On appelle substrat ces ressources nutritives provenant de la pollution. Comprendre les relations entre les quantités de substrat absorbées et les vitesses de croissance est capital mais impossible à réaliser au niveau individuel. Comment mesurer l’accroissement de la masse d’une bactérie de la taille d’un micron ? C’est ici qu’interviennent les modèles de la dynamique des populations. En faisant l’hypothèse, très raisonnable, que tous les individus d’une même espèce sont pratiquement identiques et l’hypothèse, plus problématique, nous y reviendrons, que tous les individus ont un accès identique aux ressources nutritives, on peut remplacer la mesure de la croissance d’un individu par la mesure de la croissance de toute une population. Ainsi, en déposant quelques individus sur un gel, on peut observer à l’œil nu le développement de la colonie sous la forme d’une tache de plus en plus grosse.
Pour identifier efficacement les paramètres d’un modèle de croissance des micro-organismes, compte-tenu de la quantité de substrat disponible, des chercheurs, Jacques Monod d’une part et Aaron Novick et Leo Szilard d’autre part, ont mis au point un dispositif expérimental appelé chémostat. Ce dispositif fonctionne comme un « réacteur » alimenté par un liquide contenant le substrat en concentration constante. Dans le réacteur, supposé « parfaitement homogène », les micro-organismes consomment le substrat et le volume est maintenu constant grâce à un débit sortant égal au débit d’entrée.
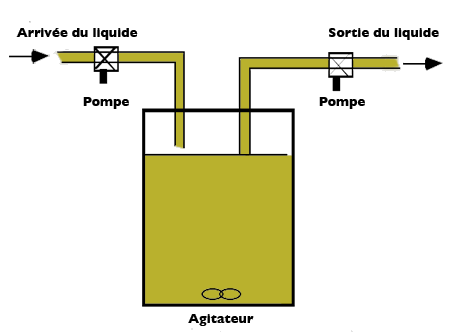
Schéma de principe du chémostat.
À ce dispositif expérimental correspond un modèle mathématique de l’accroissement relatif de la quantité de micro-organismes. La quantité de micro-organismes présents dans le volume à chaque instant est notée X. Le « taux de croissance » des micro-organismes (leur croissance rapportée à leur masse totale) est une fonction de la quantité de substrat disponible, notée S. Cette fonction est appelée « modèle de Monod ».
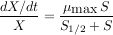
C’est une fonction nulle pour S=0, croissante, majorée par µmax et qui prend la moitié de sa valeur pour S=S1/2. Le problème est de déterminer (on dit « identifier ») les constantes µmax et S1/2 qui apparaissent dans le modèle.
Pour un volume unitaire, deux autres paramètres sont à prendre en compte, le débit du flux qui traverse le réacteur, noté Q, et la concentration du substrat en entrée, notée Sin. Le modèle général est en fait un système de deux équations, l’une exprimant la variation de la quantité de substrat, l’autre la variation de la quantité de micro-organismes. Ces équations sont des équations dynamiques qui expriment les vitesses de variation de la quantité de substrat et de micro-organismes.
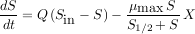 |
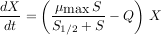 |
On peut noter que la deuxième équation correspond au modèle de Monod quand le débit est nul (Q=0).
Ce système d’équations, bien que non linéaire et n’ayant pas de solutions analytiques, repose sur une théorie mathématique simple enseignée dans les cours de génie des bioprocédés.
À l’équilibre, la quantité de substrat, notée Se, est liée au débit, noté Q, uniquement en fonction des deux paramètres, le taux de croissance maximal des micro-organismes, noté µmax, et la quantité de substrat pour le taux de croissance moitié de la valeur maximale, notée S1/2, selon une relation qui s’écrit mathématiquement de la façon suivante :
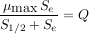
En mesurant la quantité de substrat et en faisant varier le débit, on peut donc déterminer avec précision les valeurs des paramètres du modèle que sont µmax et S1/2.
… aux procédés de traitement des eaux

Un réacteur de dépollution.
En première approximation, un procédé de traitement des eaux ne serait qu’un « gros » chémostat. Par conséquent, le modèle qui a donné de bons résultats pour comprendre la croissance d’une population isolée dans les conditions du laboratoire sera extrapolé sans vergogne à tout l’écosystème microbien en place dans un réacteur de dépollution. Ainsi, le substrat sera considéré dans son ensemble, toutes espèces chimiques confondues. De même, l’ensemble des micro-organismes présents dans le réacteur, toutes espèces confondues, sera appelé biomasse. La concentration de biomasse naturelle, mélangée à la pollution et présente à l’entrée du procédé, sera également mesurée. La variation du substrat sera alors considérée comme égale à la quantité de substrat qui entre dans le réacteur, moins ce qui en sort, moins ce qui est consommé par la biomasse. La variation de biomasse, quant à elle, sera considérée comme égale à la quantité de biomasse qui entre dans le réacteur, plus la quantité de substrat consommée par la biomasse dans le réacteur, moins la quantité de biomasse qui sort du réacteur. La quantité de substrat consommée est calculée par une fonction qui décrit le taux de croissance de la biomasse, il peut s’agir d’un modèle de Monod, mais pas nécessairement.
On écrira ainsi :
|
Variation de S égale ce qui entre moins ce qui sort moins ce qui est consommé par X |
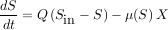 |
|
Variation de X égale ce qui entre plus ce qui est consommé moins ce qui sort |
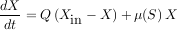 |
Malheureusement, ce modèle rencontre très vite ses limites. Pour commencer, la vision qui passe d’un substrat multiple à une biomasse multiple est beaucoup trop simpliste. En réalité, une part importante de la pollution carbonée ou azotée disparaît sous forme de gaz (CO2, méthane, azote gazeux). Et, surtout, il n’y a pas une seule « réaction », qui transformerait directement le substrat consommé par la biomasse en biomasse, mais un schéma réactionnel complexe tel que dans une première réaction, une première biomasse (on parlera ici de consortium microbien) X1 consomme le substrat S1 et produit, en même temps qu’elle croît, un second substrat S2, qui sera à son tour consommé par un consortium microbien d’un autre type, noté X2, etc.
S2 + X2 → X2
Prenons par exemple le cas de la digestion anaérobie. Ce processus biologique décrit une fermentation en conditions anaérobies, c’est-à-dire sans apport d’oxygène. Les connaissances s’accumulant au cours du temps, on est passé d’une vision impliquant seulement un consortium bactérien transformant la matière organique en gaz carbonique et en méthane à une vision « trophique », dans laquelle plusieurs consortiums bactériens interviennent successivement. Ce processus commence à être bien compris et une description « microbiologique » actuelle ferait intervenir une bonne vingtaine de « niches écologiques » interconnectées par des échanges de substrats produits. Cependant, il n’est pas nécessaire d’aller dans un tel degré de détail (de toutes façons inaccessible à la mesure, et donc invérifiable) pour obtenir une description macroscopique « satisfaisante ». Aussi surprenants soient-ils, de récents travaux ont montré que considérer seulement deux consortiums bactériens associés à deux phases réactionnelles – une première phase dite acidogénèse en cascade avec une seconde phase dite méthanogénèse – permettait de donner à un modèle de bonnes capacités prédictives, y compris sur le long terme (moyennant l’ajustement de quelques paramètres).
Un modèle de ce type de procédé sera plus complexe que le modèle du chémostat, notamment avec des équations plus complexes, mais, surtout, va dépendre de beaucoup plus de paramètres qu’il faudra identifier. On peut donc ainsi complexifier les modèles en écrivant des réactions de plus en plus détaillées, sinon réalistes.
Continuer à complexifier les modèles comme nous l’avons expliqué ci-dessus est une activité légitime car elle permet, petit à petit, d’affiner la précision de nos modèles. Et donc, pour en revenir à la demande sociale, à améliorer de quelques pour cent l’efficacité d’une station d’épuration. C’est donc une activité qui est fortement encouragée.
On pourrait même imaginer de vastes programmes chargés d’identifier tous les micro-organismes présents, de déterminer en laboratoire chaque taux de croissance et de construire des modèles avec des centaines d’équations. La puissance de calcul des ordinateurs actuels n’est pas un facteur limitant d’un tel programme.
Mais tout cela ne servirait pas à mieux comprendre ce qui se passe, car les équations utilisées sont « fausses ».
Trouver les bonnes équations : la modélisation qualitative
Il se trouve, en effet, que le modèle du chémostat est faux dès qu’on quitte les limites strictes de ce pour quoi il a été conçu. Pour le montrer, appliquons les mêmes principes que ceux qui nous ont guidés dans sa construction à la fabrication d’un modèle de croissance de deux populations en compétition pour un unique substrat. Nous appelons µ1 et µ2 les taux de croissance respectifs des deux espèces.
Or le modèle du chémostat prédit qu’à l’équilibre, une seule des deux espèces sera présente. C’est ce qu’on appelle le principe de l’exclusion compétitive. La raison mathématique en est très simple. Si nous souhaitons un équilibre où les deux espèces sont présentes, il faut qu’ on ait simultanément :
et µ2(S) – Q = 0
Ceci est impossible lorsque les taux de croissance µ1 et µ2 sont différents, donc correspondent à deux espèces « différentes ». Plus généralement, le principe d’exclusion compétitive dit que dans un système où plusieurs espèces sont en compétition pour différentes ressources, le nombre d’espèces qui peuvent cohabiter est au plus égal au nombre de ressources, les autres étant éliminées. Qu’en est-il dans la réalité ? Cette prédiction du modèle a été corroborée expérimentalement, à l’aide de chémostats de laboratoire. Mais le laboratoire n’est pas la « vraie vie », et il a par exemple été fait remarquer que dans des lacs de montagne, un très grand nombre d’espèces coexistent pour un nombre très faible de ressources « essentielles ». Dans le cas des réacteurs de traitement des eaux, nous savons de façon indubitable, grâce aux méthodes modernes d’investigation permises par la biologie moléculaire que quelques centaines, voire quelques milliers d’espèces peuvent se partager un « unique » substrat. Or cette propriété d’exclusion du modèle est « qualitative » en ce sens qu’elle ne dépend pas de la complication des fonctions de taux de croissance que l’on pourrait choisir. C’est la structure même du modèle qui est inadéquate pour représenter, ne serait-ce que qualitativement, le phénomène observé de coexistence des espèces. Il faut changer la structure du modèle, afin de trouver des équations plus satisfaisantes.
Quels sont les liens entre le modèle et la réalité ? Les données relevées sur le terrain bien sûr !
Les modèles élaborés s’appuient tout d’abord sur des hypothèses fortes de structure qui garantissent, par l’analyse mathématique, que certaines propriétés fondamentales sont respectées : par exemple, conservation de la masse totale, positivité des variables représentant des concentrations ou des effectifs, compétition ou coopération entre micro-organismes… Les modèles mettent également en jeu un ensemble de paramètres ou coefficients, sur lesquels le discours mathématique va permettre de discuter : « si on augmente le coefficient d’affinité de l’espèce A sur la nourriture de B, alors le ratio des effectifs A/B va augmenter », etc. Mais, pour obtenir des prévisions chiffrées, il est nécessaire d’affecter, avec la plus grande précision possible, des valeurs à ces paramètres. Cet ajustement s’effectue en comparant les sorties du modèle avec les grandeurs réelles mesurées. C’est ce qu’on appelle l’identification du modèle.
Son principe repose sur un schéma qui permet de minimiser l’écart entre le signal de sortie prédit par le modèle et la valeur mesurée expérimentalement.
Soit y̅θ(t) le signal de sortie prédit par le modèle pour une valeur θ d’un paramètre, et y(t) le signal observé dans la nature. On considère un critère mathématique de distance entre les fonctions y̅θ et y, par exemple la somme des carrés :
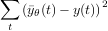
L’identification consiste alors à déterminer la meilleure valeur du paramètre θ au sens de ce critère, c’est-à-dire la valeur θ qui minimise la distance entre les fonctions y̅θ et y, parmi toutes les valeurs plausibles de θ. Il s’agit d’un problème d’optimisation dont la résolution devient très vite ardue dès que le nombre de paramètres à identifier augmente, et qui fait en général appel à du calcul intensif sur ordinateur.
La recherche de la meilleure valeur θ qui permet au modèle de « coller » au mieux à la réalité observée cache un problème plus structurel : existe-t-il toujours une seule meilleure valeur possible, ou bien plusieurs valeurs de θ peuvent-elles ajuster aussi bien le modèle ? La réponse à cette question repose sur la théorie de l’identifiabilité du modèle.
Pour une structure de modèle et un type de sortie choisis, un paramètre θ est dit identifiable si deux valeurs distinctes θ1 et θ2 génèrent en sortie des fonctions y̅θ1 et y̅θ2 distinctes. Cette propriété intrinsèque du modèle, et non des données, est une condition nécessaire pour garantir que la procédure d’ajustement conduise à une seule et unique valeur du paramètre θ, et donc à des prévisions fiables du modèle.
Lorsque cette condition d’identifiabilité n’est pas vérifiée, cela signifie que les sorties du modèle ne sont pas assez « riches » par rapport au nombre de paramètres du modèle. On peut alors soit modifier ou simplifier le modèle, soit enrichir les sorties (c’est-à-dire considérer d’autres mesures ou d’autres capteurs sur l’écosystème) pour se ramener à une situation identifiable.
Une nouvelle piste : la ratio-dependence
Dans le modèle proie-prédateur classique (on préfère ici dire ressource-consommateur), dont le modèle du chémostat est un cas particulier, le mode de croissance de la ressource est plus général que celui de la seule migration (le substrat qui entre et sort du chémostat pouvant être assimilé à une migration). Dans ce contexte, la fonction ? s’appelle la « réponse fonctionnelle ». Ce modèle, qui fait aussi intervenir une valeur m permettant de contrôler le niveau auquel le taux de croissance s’arrête, s’écrit mathématiquement :
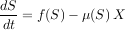 |
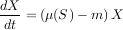 |
Si ce modèle est pris pour représenter une chaîne trophique à quatre niveaux, et si l’on suppose que le premier niveau a un taux de croissance constant U, le modèle prédit qu’un équilibre va s’établir. Que se passe-t-il pour cet équilibre lorsqu’on augmente le paramètre U qui représente la productivité primaire du milieu ? La réponse est très curieuse : seule la quantité de prédateurs supérieurs réagit proportionnellement à une augmentation de la productivité primaire.
|
Niveau trophique
|
1
|
2
|
3
|
4
|
|
Réponse de l’équilibre
|
Fonction décroissante de U
|
Croissance explosive
|
Constant
|
Croissance proportionnelle
|
Comment expliquer la diminution du premier niveau ? En 1989, les chercheurs Roger Arditi et Lev R. Ginzburg ont proposé de changer la structure du modèle classique, appelé prey-dependent, en un modèle appelé ratio-dependent. Rien n’est changé, sauf que la réponse fonctionnelle n’est plus une fonction de la quantité de proies, mais une fonction de la quantité moyenne de proies par individu, c’est-à-dire le ratio entre le nombre de proies et le nombre de prédateurs.
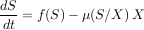 |
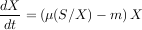 |
On vérifie aisément que dans ce nouveau modèle ratio-dependent, la réponse à une augmentation de la productivité du niveau 1 est l’augmentation de chacun des niveaux, ce qui est une prédiction plus conforme à ce qui est généralement observé. Notons bien que la meilleure adéquation à la réalité n’est pas obtenue par une augmentation du nombre des paramètres, qui reste rigoureusement le même, mais par un changement radical de la structure du modèle.
Afin de mieux cerner la différence entre les modèles dont il vient d’être question, on peut tenter un parallèle avec ce qui se produit lorsque, d’une représentation géocentrique du mouvement des astres, on passe à une représentation héliocentrique. On peut toujours, en compliquant les systèmes de cercles roulant les uns sur les autres, rendre compte de plus en plus fidèlement de la trajectoire observée des planètes, il n’empêche que c’est la révolution copernicienne qui a permis d’avancer. Autrement dit, ce n’est pas la complexification progressive du modèle qui a été la solution, mais un changement radical de point de vue. Dans le cas de la ratio-dependence, le nouveau point de vue a été l’objet de vives polémiques qui maintenant sont apaisées. Il est admis aujourd’hui que les points de vue prey-dependent et ratio-dependent ont chacun leur domaine de validité et que ce qui importe, c’est d’en préciser au mieux les limites.
C’est l’article suivant qui a le premier introduit le concept de ratio-dependence :
Arditi R., L. R. Ginzburg (1989) Coupling in Predator-Prey Dynamics : Ratio-Dependence, J. Theor. Biol , 139 : 311 – 326
Parce qu’il proposait un changement radical dans la structure du modèle couramment admis, cet article a déclenché un vive polémique, dont les titres d’articles que nous avons sélectionnés ci-dessous donnent une idée.
Arditi R., L. R Ginzburg, N. Perrin (1992) Scale invariance is a reasonable approximation in predation models – reply to Ruxton and Gurney, Oikos, 65 : 336 – 337
Diehl S., P. A. Lundberg, H. Gardfjel, L. Oksanen, L. Persson (1993) Daphnia – phytoplancton interactions in lakes, is there a need for ratio-dependant consumer ressources models ? Am. Nat. vol 142, pp. 1052-1061
Abrams P. (1994), The fallacies of « Ratio-dependent » predation, Ecology, 75 : 1842 – 1850
Akçakaya H. R., Arditi R. L. R Ginzburg (1995), Ratio-dependent predation : an abstraction that works, Ecology, 76 : 995 – 1004
Berryman A. A., A. P. Gutierrez, R. Arditi (1995), Credible, parsinomious and usefull predator-prey models – A reply to Abrams, Gleason and Sarnelle, Ecology, 76 : 1980 – 1985
Abrams P. (1997) Anomalous predictions of ratio-dependent models of predation, Oikos 80 : 163 – 171
L’écologie théorique est une science bien vivante !
La ratio-dependence dans les modèles de compétition
Les mathématiques et la modélisation ont l’immense avantage sur les sciences expérimentales que la moindre idée nouvelle peut être immédiatement explorée, sans avoir besoin de réunir des moyens financiers considérables. On peut même, grâce aux simulations sur ordinateur, aller très au-delà de ce que permet notre simple habileté mathématique. C’est ce que nous avons entrepris dans le cadre de notre projet, en étudiant les propriétés du modèle de compétition de type ratio-dependent. En remplaçant les fonctions S → µ1(S) et S → µ2(S) du modèle classique, dépendantes des ressources, par des fonctions qui prennent en compte les deux espèces 1 et 2 en compétition, nous obtenons le nouveau modèle suivant :
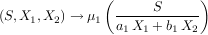 |
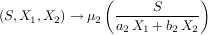 |
Nous avons pu expliquer le rôle des paramètres a1, a2, b1, b2 du nouveau modèle. Nous montrons en effet que si la compétition à l’intérieur d’une même espèce (mesurée par a1,b2) est plus forte que la compétition entre espèces différentes (mesurée par b2,a1), alors il peut y avoir coexistence des deux espèces. Ce résultat est valable pour un nombre quelconque d’espèces.
 |
 |
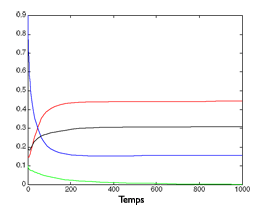 |
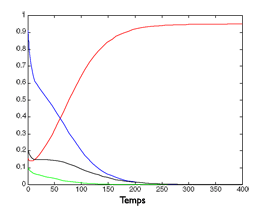
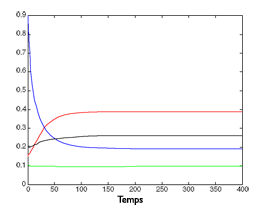
Simulation de l’évolution de quatre espèces.
Ci-dessus à gauche, évolution de quatre espèces au cours du temps dans un modèle dépendant des ressources. L’espèce « rouge » remporte la compétition.
Au centre, le même modèle, mais dépendant du ratio entre ressources et consommateurs, avec une très forte compétition interne à chaque espèce : les quatre espèces subsistent.
À droite, toutes choses égales par ailleurs, on fait diminuer la compétition interne aux espèces, au profit de la compétition entre espèces. L’espèce « verte » ne résiste pas et disparaît.
Bien entendu, il ne suffit pas de produire un modèle qui satisfasse quelques fantasmes de mathématiciens pour que ce modèle ait une valeur scientifique. Il faut qu’il respecte à son tour des critères de cohérence interne, qu’il soit interprétable et que ces interprétations soient confrontées à des données empiriques. Dans notre cas, la ratio-dependence généralisée que nous avons introduite peut s’interpréter comme la diminution, quand augmente la biomasse, de la quantité de biomasse effectivement active. Il faut tester ce genre d’hypothèse. C’est un travail en cours dans le cadre de nos collaborations avec d’autres collègues du domaine : bien que les questions soient assez simples et l’objet de la recherche bien délimité, le travail à cette échelle est compliqué et nécessite la mise en commun de nombreuses compétences.
La démonstration expérimentale, solution de tous les problèmes ?
La démonstration expérimentale de la ratio-dependence sera-t-elle la solution de tous les problèmes de dépollution biologique ?
On se doute bien que non ! Finalement, un réacteur biologique de dépollution est un écosystème d’une inimaginable complexité. Des centaines d’espèces ayant des fonctions différentes sont présentes. Certainement, aucun des deux modèles que nous venons d’évoquer à propos de la ratio-dependence, que ce soit la chaîne trophique, organisation purement verticale, ou la compétition pour une ressource, organisation purement horizontale, ne reflète à lui seul correctement la réalité.
En réalité, les niveaux trophiques ne sont pas nettement séparés (un prédateur en compétition avec un autre sur une ressource peut aussi être un prédateur de ce prédateur), certaines espèces produisent des molécules qui peuvent être consommées par d’autres, loin d’être des individus mobiles et isolés, les bactéries s’organisent et fabriquent des biofilms, sortes de matrices à l’intérieur desquelles elles circulent. Et puis, nous n’avons pas parlé des virus qui viennent compliquer la donne. Enfin ces cellules, qui certes ne sont pas des êtres vivant au Q.I. très développé, sont quand même munies de moyens de communication. Nous sommes décidément bien loin du modèle du chémostat et de quelques avatars plus ou moins complexes. Nous pourrions continuer à développer longtemps cette vision et alimenter ainsi le double discours pessimiste auquel nous sommes souvent confrontés. Celui des mathématiciens : « toutes ces choses sont belles et fascinantes, mais bien trop compliquées pour que nous puissions en dire quoi que ce soit de mathématiquement propre » et celui des biologistes : « votre modèle est simpliste, il ne tient pas compte de tel fait capital ».
À ce pessimisme, nous opposons invariablement les quelques arguments qui nourrissent notre optimisme.
- Faire un modèle d’un procédé de traitement des eaux, ce n’est pas faire un modèle qui répondra à toutes les questions de biologie et d’écologie théorique, mais plus modestement, aider à répondre à quelques questions concrètes comme : « pour tel procédé, est-il préférable de travailler avec un seul réacteur ou deux réacteurs en cascade ? »
- C’est une évidence de dire que c’est parce qu’ils développent des instruments nouveaux d’observation des écosystèmes microbiens que les microbiologistes peuvent nous parler de leur complexité. Mais ces instruments (SSCP, etc.), même s’ils sont encore très imparfaits, permettent de suivre l’évolution de certains écosystèmes en continu et en laboratoire. C’est une situation très nouvelle en écologie théorique. On peut penser qu’elle sera féconde.
La SSCP (Single Strand Conformation Polymorphism) est une technique de biologie moléculaire basée sur le fait qu’une séquence du génome des micro-organismes (appelée ADNr 16S) « code pour l’espèce » (en fait, il s’agit d’une séquence différente pour chaque espèce dont on a pu montrer que la probabilité de muter était très faible).
Après extraction des ADN totaux d’un mélange de micro-organismes et amplification par PCR (Polymerase Chain Reaction), la technique SSCP permet d’obtenir une empreinte moléculaire des écosystèmes microbiens en séparant les molécules d’ADNr 16S en fonction de leur séquence. Une communauté microbienne complexe est alors représentée sous la forme d’un profil où, sous certaines conditions, il est possible d’affirmer que chaque pic correspond à une séquence, et par extension, à une espèce.
Cette « empreinte moléculaire » permet donc de caractériser – sans mise en culture – la diversité d’une microflore, de comparer des microflores semblables, d’en suivre la dynamique en terme de présence grâce à l’ADNr 16S et/ou en terme d’activité grâce à l’ARNr 16S.
- Il est maintenant possible de faire des modèles de petits écosystèmes, où chaque cellule est représentée individuellement avec la liste de ses attributs fonctionnels et de faire tourner l’ordinateur pour en obtenir une simulation. La difficulté est d’interpréter correctement les résultats de la simulation. Des équipes y travaillent et elles progressent.
- Nul n’est à l’abri d’une bonne surprise. Peut-être qu’un changement radical de point de vue éclairera considérablement le paysage.
À vrai dire, si nous devions avoir quelque pessimisme, il viendrait plutôt des conditions dans lesquelles la recherche s’exerce de nos jours. Nous avons montré à quel point notre travail, dont la finalité est on ne peut plus concrète, dépend de façon cruciale d’avancées de ce qu’on appelle la recherche fondamentale. Il est probablement bon de le répéter car, aujourd’hui, au nom de la « demande sociale », la science semble devoir massivement s’orienter vers la recherche appliquée, ou à la rigueur rester fondamentale, mais certainement jamais les deux à la fois, alors que ces deux aspects ne vont pas l’un sans l’autre. Chaque époque a ses obscurantismes.
- Bernard, O., Hadj-Sadok, Z., Dochain, D., Genovesi, A. et Steyer, J.-P. (2001) : « Dynamical model development and parameter identification for anaerobic wastewater treatment process », Biotechnology and Bioengineering, 75(4):424-438
- Loisel, P., J. Harmand, O. Zemb, E. Latrille, C. Lobry, J. P; Delgenes et J. J. Godon (2006) « DGE and SSCP molecular fingerprintings revisited by simulation and used as a tool to measure microbial diversity », Environmental Microbiology, Vol. 8, No. 4, pp. 720-731.
- Walter, E., et L. Pronzato (1997) « Identification of Parametric Models: From Experimental Data », Springer.
- Lobry, C., F. Mazenc et A. Rapaport (2005) : « Persistence in ecological models of competition for a single resource », CRAS série Mathématiques, Vol. 340, pp. 199-204.
- Lobry, C. et J. Harmand (2006) : « A new hypothesis to explain the coexistence of N species in the presence of a single resource », CRAS série Biologie, Vol. 329, pp. 40-46.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jérôme Harmand

Claude Lobry

Alain Rapaport