Classer musiques, langues, images, textes et génomes
Lorsque vous répétez une histoire qu’on vient de vous raconter, vous ne la reproduisez pas à l’identique, mais entre ce que vous dites et ce que vous avez entendu, de nombreux points correspondent, et, pour l’essentiel, les récits coïncident : la version initiale et la version reproduite possèdent un fort contenu commun en information en termes de mots (ou racines de mots), de longueurs de phrases, de répétitivité des textes, etc. Cette notion de « contenu commun en information » semble imprécise et l’on imagine mal qu’il soit possible d’en formuler une définition générale, encore moins qu’on puisse lui associer un nombre. Pourtant, c’est l’exploit que mathématiciens et informaticiens réussissent aujourd’hui par la mise en œuvre d’une idée simple tirée d’une théorie dont les mathématiciens pensaient qu’elle était… inapplicable.
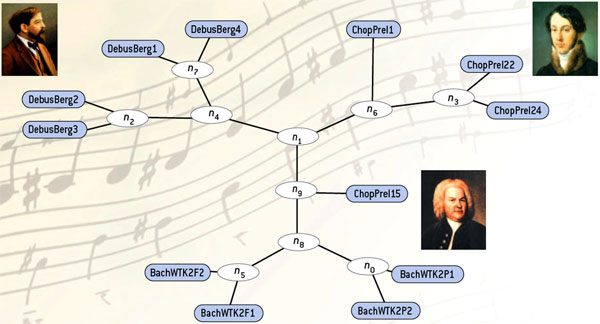
En faisant travailler les algorithmes de compression sur les musiques de Bach, de Debussy et de Chopin, on définit des distances entre différentes œuvres de ces musiciens (toujours comparées par paires). À partir de ces distances, on construit un arbre où les musiques de chacun sont « par miracle » automatiquement regroupées. L’analyse par compression dégage les caractéristiques spécifiques de chaque musicien en construisant un arbre fondé sur les distances déterminées par les éléments communs de chaque paire. Ces regroupements ont été faits « en aveugle » avec un programme de compression non adapté à la musique.
Infographie : Pour la Science
On sait depuis Maxwell qu’information et thermodynamique sont intimement liées, notamment par l’entropie qui mesure le désordre d’un système, mais certaines considérations des physiciens se sont révélées précipitées. En 1950, John von Neumann émit l’idée que toute opération binaire de calcul menée à la température T dissipait une quantité d’énergie de KB T ln 2 (où KB est la constante de Boltzman qui vaut 1,3805 x 10-23 joule par degré Kelvin) accroissant donc l’entropie de KB ln 2. Cette idée s’est révélée en partie fausse.
Les travaux de Rolf Landauer montrèrent en effet que seule l’opération d’effacement (irréversible) d’une information binaire avait un tel coût thermodynamique. Ainsi, une porte classique (a) dissipe de l’énergie, car elle perd des informations : quand l’état d’une ligne de sortie est 0, on ne peut en déduire l’état des lignes d’entrée. Au contraire, la porte logique réversible de Frekin (b) ne dissipe pas l’énergie : deux bits de sortie, les bits de déchets C et D, permettent de faire fonctionner la porte en sens inverse afin de ramener l’ordinateur dans son état initial.
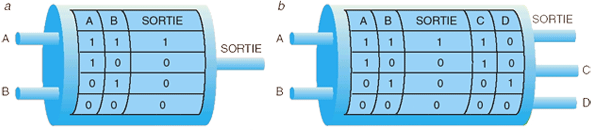
Toute opération binaire réversible peut être ainsi menée avec un coût thermodynamique nul. Complétant ce résultat, il a été établi par Y. Lecerf en 1963, puis indépendamment par Ch. Bennett en 1973, que tout calcul peut être mené de manière réversible, et donc, sans coût thermodynamique. L’inconvénient des calculs réversibles est qu’ils conduisent à accumuler une sorte de déchet d’information : cette accumulation est créée par l’impossibilité d’effacement qui oblige à conserver des informations parfois devenues inutiles et encombrantes.
Les méthodes de correction d’erreurs très utilisées aujourd’hui et dont on voit mal comment on pourrait se passer pour mener des calculs fiables sont malheureusement des opérations fondamentalement irréversibles. La raison en est que corriger une erreur, c’est l’effacer. S. Lloyd a calculé qu’un ordinateur ultime d’un kilogramme et d’un litre opérant à 1051 opérations par seconde (vitesse indépassable) devrait avoir un taux d’erreur inférieur à 10-10 pour éviter la surchauffe, mais que même avec ce taux très faible, toute l’énergie du système serait dissipée pour opérer la correction d’erreur en moins d’une nanoseconde !
Dans la décennie 1990, partant de considérations sur le calcul réversible, une équipe de théoriciens autour de Charles Bennett inventa la distance informationnelle qui dépend du contenu commun en information. Elle fut utilisée dès 1998 par l’équipe de bioinformatique du Laboratoire d’informatique fondamentale de Lille pour classer des séquences génétiques : la distance informationnelle entre deux suites de caractères A et B est définie par la taille du plus court programme permettant de transformer A en B et B en A. Peu après, cette méthode, reprise par des chercheurs de l’Université d’Amsterdam autour de Paul Vitanyi, fut perfectionnée et simplifiée sous le nom de distance de similarité. Aujourd’hui, les succès de cette idée concernent une multitude de domaines. Plus étonnant encore, les dernières versions de la méthode sont faciles à mettre en œuvre et sont adaptables à toutes sortes de problèmes grâce à des logiciels du domaine public.
La distance de similarité a été appliquée à la classification des langues, des morceaux de musique, des textes (dont en particulier les chaînes de lettres), des images et des données astronomiques. Le logiciel FindFraud exploitant cette distance permet de repérer les étudiants qui copient : vous entrez les textes des devoirs de toute la classe, l’algorithme vous indique les suspects, à vous alors de juger si les ressemblances repérées sont excessives et de punir les plagiaires. Cela est applicable aussi à des morceaux de musique et à des œuvres littéraires, comme nous le verrons.
Compression de données
La mesure numérique du contenu commun en information est obtenue en utilisant des algorithmes de compression de données : meilleurs sont les algorithmes utilisés, plus fines seront les classifications obtenues. Ces algorithmes fournissent la valeur du contenu commun en information de deux objets en exploitant une formule que nous allons détailler, car elle est au cœur de l’idée de la classification par compression.
On choisit un algorithme de compression C, dont, si possible, on sait qu’il fonctionne avec efficacité sur les données qu’on veut classer (textes, partitions musicales, séquences d’ADN…). Cet algorithme de compression doit être sans perte, ce qui signifie que si C, appliquée à la suite de caractères A, produit la suite comprimée B, alors en appliquant à B le décompresseur de C, on reconstituera exactement A. L’algorithme gzip, bien connu des utilisateurs de micro-ordinateurs, est un tel algorithme de compression que l’on peut utiliser pour tout fichier informatique. Il en existe une multitude d’autres, certains spécialisés dans les fichiers de séquences génomiques, d’autres dans les fichiers de son, d’image ou de film.
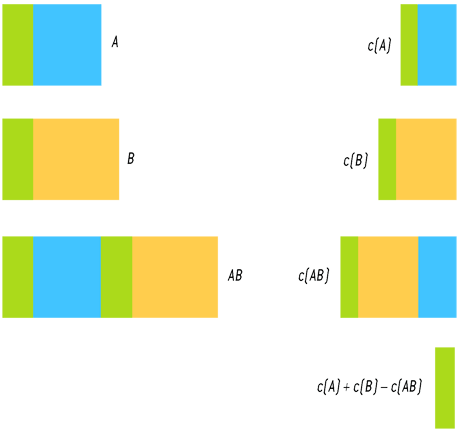
Évaluation du contenu commun en information à deux ensembles de données. On considère deux ensembles des données A et B (deux textes, deux morceaux de musique ou deux séquences d’ADN, etc.). L’ensemble des données A comporte des informations qui lui sont spécifiques (en bleu) et des informations qu’il partage avec l’ensemble de données B (en vert). De même, les informations de B se décomposent en une partie spécifique à B (en jaune) et la partie commune. Les versions comprimées de A et de B similairement comportent des parties spécifiques et des parties communes. Lorsque l’on comprime la concaténation de A et de B (notée AB), la partie commune à A et B n’est bien sûr pas dupliquée, car la compression supprime les redondances, et donc la version comprimée de AB comporte une partie correspondant à la version comprimée de la partie bleue, une autre pour la version comprimée de la partie jaune (spécifique à B) et une dernière pour la version comprimée de la partie verte. Les longueurs des données comprimées c(A), c(B) et c(AB) mesurent les contenus en information de A, de B et de AB. Le schéma illustre que l’expression c(A) + c(B) – c(AB) se simplifie et qu’on obtient comme résultat une mesure du contenu commun en information à deux ensembles de données, on en déduit une distance qui vaudra 0 (approximativement) lorsque A et B auront le même contenu en information et qui prendra une grande valeur lorsque A et B seront peu corrélés.
Infographie : Pour la Science
Le compresseur C choisi, on l’applique aux données à classer et l’on mesure la longueur des versions comprimées par l’algorithme C appliqué à A, à B et à AB (A suivi de B). Ces longueurs correspondent à trois nombres c(A), c(B), c(AB) qui indiquent les contenus en information de A, de B et de AB et on examine la différence {c(A) + c(B) – c(AB)}.
Lors du calcul de c(AB), les informations communes à A et B ne sont comptées qu’une seule fois : quand, après avoir comprimé A, il comprime B, le compresseur élimine l’information redondante qui était déjà dans A. Les informations propres à A et celles propres à B ne sont donc comptées qu’une fois dans c(AB). En revanche, lorsque l’on calcule à part c(A) et c(B), on comptera une fois les informations propres à A, une fois les informations propres à B et deux fois les informations communes à A et B (une fois lors du calcul de c(A) et une fois lors du calcul de c(B)).
Le calcul de la différence {c(A) + c(B) – c(AB)} se simplifie et il n’en reste finalement qu’un seul terme : le contenu commun en information de A et B. Dit autrement, l’économie d’espace que l’on obtient quand on comprime AB en une fois, comparée à des compressions séparées de A, et de B, est une mesure du contenu commun en information de A et B.
On définit alors la distance de similarité entre les séquences A et B. Si c(B) ≤ c(A), la distance entre A et B vaut : d(A, B) = 1 – {c(A) + c(B) – c(AB)}/c(A) ; si c(A) ≤ c(B), elle vaut : d(A, B) = 1 – {c(A) + c(B) – c(AB)} / c(B).
Les dénominateurs apparaissant dans les formules sont des facteurs de normalisation, qui ne jouent un rôle important que quand on manipule des données A et B de tailles très différentes. La quantité d(A, B) est comprise entre 0 et 1 et possède les propriétés de ce que les mathématiciens nomment une distance :
|
d(A, B) = 0 si et seulement si A = B ;
|
|
d(A, B) = d(B, A) (symétrie) ;
|
|
d(A, B) ≤ d(A, C) + d(C, B) (inégalité triangulaire).
|
Avec des compresseurs habituels, certaines de ces propriétés ne sont vraies qu’approximativement, mais cela n’est pas très grave, l’essentiel se trouvant dans l’interprétation de la quantité d(A, B). Si A et B sont sans rapport (par exemple deux séquences aléatoires de pile ou face, ou deux textes sans liens dans des langues différentes), alors le contenu commun en information de A et B est nul, c(AB) = c(A) + c(B) et donc d(A, B) = 1, la valeur maximale de la distance. Si, en revanche, A = B, alors c(A) = c(AB) = c(B) et donc d(A, B) = 0.
Ainsi, plus le contenu commun en information de A et B est grand, plus petite est la distance d(A, B) ; plus les séquences A et B sont indépendantes (sans corrélation), plus d(A, B) s’approche de 1. Les corrélations peuvent être de nature statistique ou résulter de la présence de séquences communes en fonction des compresseurs utilisés.
Justification théorique profonde
En expliquant la distance de similarité comme nous venons de le faire, des points paraissent peut-être mystérieux ou obscurs. De quelle information s’agit-il ? En changeant d’algorithme de compression, on change les résultats : le contenu commun en information serait-il variable ? Qu’est-ce qui justifie de parler d’information et de contenu commun en information ?
La réponse à ces questions se trouve dans les considérations mathématiques que permet la théorie algorithmique de l’information (ou théorie de la complexité de Kolmogorov) née dans la décennie 1960, à la frontière de la logique mathématique et de l’informatique théorique. Ce que nous avons examiné prend un sens rigoureux en considérant des méthodes de compression parfaites. L’information dont il s’agit alors est l’information algorithmique d’une suite de caractères, définie comme la taille du plus petit programme permettant de l’engendrer.
Hélas, les méthodes parfaites de compression (mentionnées par la théorie) sont des méthodes idéales dont on démontre qu’elles ne sont pas programmables : aucun algorithme ne permettra jamais de calculer les compressions optimales de la théorie algorithmique de l’information ! Le recours à des méthodes de compression particulières et imparfaites est donc inévitable. La distance de similarité définie en s’appuyant sur un compresseur particulier C n’est qu’une version approchée d’un concept mathématique définitivement inaccessible.
Le cadre théorique permet de savoir que la distance de similarité est « universelle » : dans sa version idéale, elle ne peut manquer la moindre similarité possédée par deux suites de caractères. Les versions fondées sur des compresseurs réels n’ont bien sûr pas les belles propriétés de la version idéale, mais, si le compresseur est bon, la distance d(A, B) sera une mesure approchée satisfaisante de la distance de similarité idéale. Dans une telle situation, la justification de la pratique est heuristique : le fait que la méthode théorique soit démontrée bonne suggère que ses versions approchées le sont aussi ! Reste à s’assurer que tout cela fonctionne correctement.
La distance de similarité pour un compresseur donné produit un tableau de distances mutuelles pour tous les objets à classer. Imaginons quatre objets A, B, C, D à classer. L’utilisation du compresseur nous fournit les valeurs d(A, B), d(A, C), d(A, D), d(B, C), d(B, D), d(C, D). Que faire de ces données ?
Il est clair que si nous réussissons à placer quatre points sur le plan géométrique, de façon que leurs distances au sens habituel soient celles calculées, nous aurons une représentation intéressante des rapports entre A, B, C et D, et donc du contenu commun en information des différents objets. Nous verrons d’un seul coup d’œil les objets proches ou éloignés. Il se trouve qu’une telle disposition est rarement possible. Pour être certains de placer quatre points conformément à un ensemble de distances données à l’avance (et vérifiant les propriétés énumérées plus haut), nous devrions nous placer dans un espace de dimension 3. Plus généralement, pour placer n points, il faut un espace de dimensions n – 1. Si n dépasse 5, nous n’y verrons pas grand-chose ! Comment faire ?
L’interprétation des distances
Le problème de l’interprétation de tels tableaux de distances s’est déjà posé. Notamment en biologie où, depuis longtemps, par toutes sortes de procédés, on calcule des distances entre séquences génétiques qu’on cherche ensuite à visualiser. Un exemple de distance utilisée en génétique est celui de la distance d’édition : la distance d’édition entre A et B est le nombre minimum d’opérations d’édition (délétion d’un caractère, insertion d’un caractère ou mutation d’un caractère) qu’il faut opérer à partir de A pour arriver à B.
Les biologistes ont donc mis au point des méthodes pour produire des visualisations ; Paul Vitanyi et Rudi Cilibrasi ont perfectionné l’une d’elles de manière à visualiser les tableaux de distances calculés par compression. Cette méthode conduit à dessiner une arborescence où les données A et B sont sur des branches proches lorsque d(A, B) est petit et où les données sont sur des branches éloignées lorsque d(A, B) est grand.
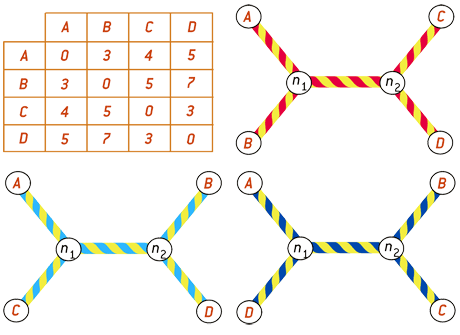
Représenter des tableaux de distances par des arbres. Imaginons que nous disposions d’un tableau de distances entre quatre objets. d(A, B) = 3 ; d(A, C) = 4 ; d(A, D) = 5 ; d(B, C) = 5 ; d(B, D) = 7 ; d(C, D) = 3 ; On désire obtenir une arborescence contenant les objets A, B, C, D qui respecte aussi bien que possible les distances mutuelles des couples d’oblets. Il existe trois façons de constituer un arbre ayant comme extrémités les objets A, B, C, D et dont les nœuds ont trois branches (les nœuds à deux branches ou à plus de trois branches sont inutiles) : AB / CD ; AC / BD AD / BC. On considère que le meilleur des trois arbres est le premier, c’est-à-dire AB / CD car d(A, B) + d(C, D) est plus petit que d(A, C) + d(B, D) et que d(A, D) + d(B, C). C’est donc ce premier arbre qu’on retiendra pour représenter le tableau de distances de notre exemple. Lorsque plus de quatre objets doivent être organisés sous la forme d’un arbre, le principe se généralise et, parmi tous les arbres possibles, l’un d’eux représente mieux le tableau des distances que les autres. Des algorithmes permettent de calculer ces meilleurs arbres.
Infographie : Pour la Science
Calculer ces arbres est un problème algorithmique assez délicat et on n’aboutit pas toujours à un arbre représentant parfaitement l’ensemble des données d(A, B), d(A, C), etc. Un coefficient Q évalue la qualité de l’arbre obtenu relativement aux données initiales et permet donc de savoir si on doit avoir une grande confiance en lui, ou seulement le considérer comme un indicateur approximatif des contenus communs en information des séquences A, B, C, etc.
Dans le cas des séquences génétiques, les arborescences produites s’interprètent comme des arbres de filiations, et on parle d’arbres phylogénétiques. Mais les arborescences obtenues peuvent aussi se voir comme des regroupements hiérarchisés lorsque l’on classe des objets n’ayant pas de relations de filiations attendues.
Ainsi, la méthode de classification par compression procède en trois étapes.
|
(a) Application de l’algorithme de compression sélectionné à toutes les suites de caractères à classer A, B, C, etc. et à toutes les doubles suites AB, AC, BC, etc.
|
|
(b) Utilisation de la formule de la distance de similarité, ce qui donne un tableau de nombres compris entre 0 et 1 : d(A, B), d(A, C), d(B, C), etc.
|
|
(c) Construction d’un arbre permettant une visualisation globale du tableau des distances et constituant une classification par regroupements hiérarchisés des données A, B, C, etc.
|
Ces trois étapes totalement automatisées conduisent, quand tout se passe bien, à un schéma représentant au mieux les similarités des objets A, B, C, etc.
La classification des langues
L’élaboration d’un arbre des différentes langues préoccupe les linguistes et il est bien sûr l’objet de nombreuses analyses et discussions. Il a servi de test à la méthode de la distance de similarité. Parmi les expériences menées par P. Vitanyi et ses collaborateurs, remarquable est leur tentative de construire un arbre de classification des 52 langues indo-européennes principales. Partant de la traduction de la Déclaration des droits de l’homme dans chacune des 52 langues, ils ont laissé leur méthode automatique mener tout le travail d’élaboration d’un arbre. L’arbre obtenu est conforme, pour l’essentiel, à ce qu’obtiennent les linguistes, ce qui est assez bon puisque ces mathématiciens et informaticiens ne disposent d’aucune compétence particulière en linguistique et que c’est finalement l’algorithme de compression utilisé qui a donc fait tout le travail de repérage des similarités entre langues.
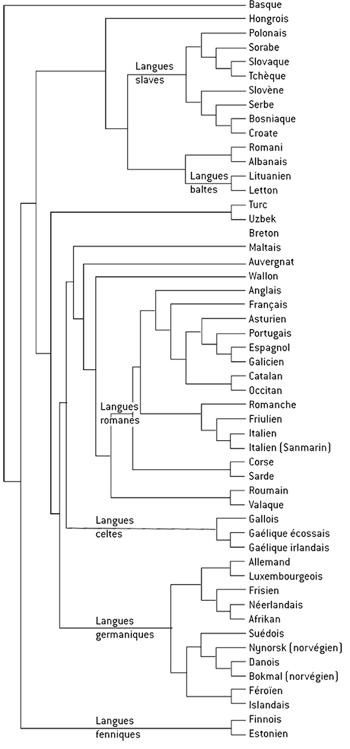
Application aux langues indo-européennes à partir des traductions de chacune des langues de la Déclaration universelle des droits de l’homme.
Infographie : Pour la Science
Trouver les auteurs
Dans le domaine linguistique, P. Vitanyi et ses collègues ont mené une autre expérience. En partant de 19 textes en russe provenant de 5 auteurs, ils ont examiné si les caractéristiques linguistiques des écrivains permettraient à une méthode par compression de regrouper correctement les textes de chaque auteur. Le résultat est très satisfaisant puisque l’arbre automatique a associé les textes en fonction de leurs auteurs à l’exception d’une œuvre de Tolstoï déplacée. La même classification réalisée à partir des traductions en anglais des mêmes œuvres donne un résultat moins bon, dû au style surimposé des traducteurs.

Distance des textes d’auteurs russes par la méthode de compression : un seul texte de Tolstoï est mal classé. Les données présentées ci-dessus sont issues des travaux de P. Vitanyi et Rudi Cilibrasi.
Infographie : Pour la Science
Des travaux de Dominique Labbé utilisant une distance fondée sur le vocabulaire commun à deux textes semblent appuyer l’idée, plusieurs fois défendue dans le passé, que Corneille serait l’auteur de certaines des pièces de Molière, sinon de toutes. Ces travaux sont aujourd’hui controversés. Grâce à la distance de similarité, une confirmation ou au contraire une infirmation des conclusions de Dominique Labbé pourrait être obtenue, permettant peut-être à la controverse de s’apaiser.
La musique
Dans le domaine musical, la méthode de classification par compression produit aussi des résultats inespérés. Partant de morceaux de musiques codés dans le format MIDI (Musical Instrumental Digital Interface), les chercheurs ont constitué des fichiers normalisés de 36 morceaux de musique. La normalisation consiste pour chaque morceau à produire une version pour piano, qui elle-même détermine un fichier de données (une suite de nombres codés sur huit chiffres binaires). Sans cette normalisation, qui est une pure extraction d’informations, rien ne fonctionnerait ; il n’y a donc pas d’espoir d’obtenir de bons résultats de classification avec les compresseurs MP3 (qui d’ailleurs sont des compresseurs avec pertes, ce que la méthode interdit). Les fichiers numériques élaborés à partir de morceaux musicaux sont confiés à la méthode automatique de classification par compression, ce qui conduit à des arbres. Ceux-ci sont conformes à ce que chacun obtiendrait en classant les morceaux en fonction de leurs ressemblances musicales.
Les séquences génétiques
Dans le domaine de la génétique, les résultats obtenus sont encore plus impressionnants et utiles car, contrairement aux domaines de la linguistique, de la musique ou de la littérature, nous ne disposons pas d’une compréhension intuitive des séquences permettant de faire les arbres sans aide. Les masses de données disponibles ne cessent d’ailleurs de croître et nul ne peut les traiter à la main.
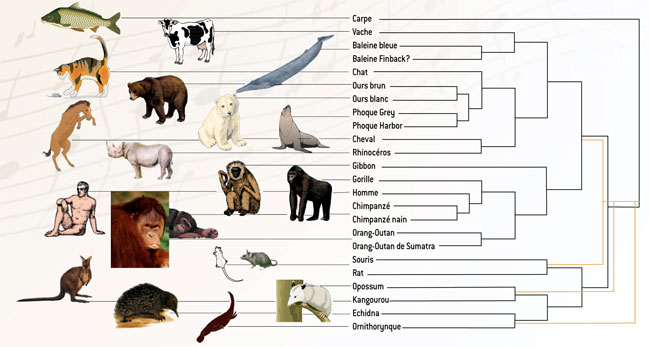
Arbre reconstituant l’évolution de 24 espèces de mammifères obtenus par compression des séquences de l’ADN mitochondrial. Cet arbre concorde avec les résultats des paléontologues à la différence près indiquée en orange. Les données présentées ci-dessus sont issues des travaux de P. Vitanyi et Rudi Cilibrasi.
Infographie : Pour la Science
Sans compression, on obtient les classifications phylogénétiques en associant des méthodes manuelles et algorithmiques. On commence dans un premier temps par effectuer un alignement des séquences qu’on veut classer. Cela consiste à placer les séquences à comparer dans un grand tableau, à raison d’une séquence par ligne, puis à s’arranger pour que des parties analogues s’alignent verticalement en introduisant, lorsque c’est nécessaire, des espaces blancs à l’intérieur des séquences. Si certaines parties ne s’alignent pas bien, on les supprime et donc une partie de l’information génétique est négligée. Les permutations entre morceaux de séquences, dont on sait qu’ils sont fréquents lors de l’évolution des séquences, ne sont pas utilisées pour effectuer ces alignements. Le plus souvent, ce travail est opéré à l’aide d’algorithmes spécialisés d’alignement, puis affiné à la main, ce qui demande des heures de travail aux spécialistes. L’alignement étant obtenu, une distance du type « distance d’édition » est utilisée pour obtenir un tableau de distances puis l’arbre est enfin produit. Ce travail ne porte généralement que sur un gène ; chaque gène fournit donc un arbre phylogénétique et ces arbres ne sont pas toujours compatibles.
Avec les méthodes par compression, tout est plus simple. Aucun alignement préalable des séquences n’est nécessaire et la perte d’informations due aux suppressions de bouts de séquences est évitée. On peut comparer des séquences contenant plusieurs gènes, voire des chromosomes entiers sans qu’aucun spécialiste n’ait à intervenir. Les permutations entre morceaux de séquences sont traitées par les algorithmes de compression et l’existence de ces mouvements est prise en compte dans le tableau de distances qui donne l’arbre final.
La méthode par compression ainsi complètement automatisée a été utilisée pour produire un arbre phylogénétique des mammifères placentaires à partir des génomes mitochondriaux complets des différentes espèces. L’arbre obtenu par la méthode automatique est conforme à l’arbre majoritairement admis par les spécialistes. C’est là un succès notable, puisque sans connaissance particulière et en mettant en œuvre une méthode ne nécessitant aucune intervention humaine, la technique de compression retrouve une phylogénie considérée comme délicate. D’autres essais portant en particulier sur les séquences du virus du SRAS confirment l’intérêt dans le domaine de la phylogénie de la méthode de classification par compression.
Plagiaires, chaînes de lettres
La ressemblance entre histoires que nous évoquions au début, la recherche de plagiaires, l’étude des chaînes de lettres (qui à mesure de leur circulation d’une personne à l’autre évoluent comme les organismes vivants évoluent), tout ce qui repose sur la recherche de contenu commun en information entre textes peut être traité par la technique de la classification par compression.
Outre FindFraud de Steven de Rooij, un autre logiciel anti-fraude pour détecter les élèves copieurs d’une même classe ou d’un même groupe a aussi été développé par Hubert Wassner. Voir Baldr, l’outil anti-fraude/anti-plagiat et télécharger ce logiciel.
Leçons
Les expériences menées prouvent que la méthode dont l’origine théorique faisait beaucoup espérer est réellement en mesure de s’adapter à des contextes variés. Quelques remarques s’imposent à propos de ces succès.
Si les algorithmes de classification par compression permettent de classer souvent aussi bien que des méthodes ad hoc utilisées jusqu’à aujourd’hui dans chaque domaine particulier, c’est qu’ils contiennent un riche savoir-faire résultant de plusieurs décennies de recherche en compression de données. Ce savoir-faire se trouve soudain mis au service de problèmes de classification. La situation est comparable à celle de la technologie électronique développée dans la première moitié du XXe siècle pour construire des appareils de radio et des réseaux téléphoniques et dont, dans la décennie 1940, on découvrit qu’elle pouvait aussi servir à fabriquer des machines à calculer. Brusquement, une technologie performante se met au service d’un nouveau problème qu’on ne pensait pas lié, et produit rapidement, à moindre coût, d’étonnants résultats. Bien sûr, comme l’électronique qui a évolué une fois son utilité découverte pour le calcul et s’est adaptée aux problèmes particuliers qu’il posait, les méthodes de classification par compression se perfectionneront dans l’avenir.
Les résultats de ce domaine confirment la profondeur de la théorie algorithmique de l’information qui se révèle un outil conceptuel remarquablement affûté susceptible de suggérer des méthodes pratiques. Même proche de l’indécidabilité (aucune théorie n’en est sans doute plus proche), on sait en extraire des idées utiles. En algorithmique, toute idée est bonne à prendre quelle qu’en soit l’origine et les théories les plus abstraites se révèlent parfois excellentes inspiratrices.
La méthode de classification par compression se comporte malheureusement comme une boîte noire : des calculs complexes sont menés par les compresseurs qui produisent des résultats donnés sans explication. Il n’est pas impossible dans le cas des compresseurs les plus simples d’extraire des calculs menés des informations précises sur le contenu commun en information des données comparées : qu’est-ce qui dans les morceaux de musique de Bach est caractéristique ? En quoi consistent les ressemblances entre les deux génomes mesurés proches par le compresseur ? Etc. Aujourd’hui, peu de travaux ont été menés dans ce sens, mais il ne fait pas de doute qu’on doit les approfondir et qu’ils apporteront un complément précieux aux résultats nus calculés via la méthode de classification par compression telle qu’on la met en œuvre.
Les mathématiciens citent l’arithmétique comme exemple de théorie qu’on ne développait que pour la beauté et la fascination des résultats qu’on y rencontre et qui, avec la cryptographie, s’est soudain révélée placée au cœur des problèmes les plus concrets de l’informatique et des télécommunications. Aujourd’hui, pour défendre leur discipline, les mathématiciens peuvent ajouter la théorie algorithmique de l’information qui, à partir de considérations abstraites sur les calculateurs universels, vient de montrer qu’elle conduisait à d’efficaces et élégants outils logiciels.
Quelques références vous sont proposées pour en savoir plus sur les algorithmes de compression de données.
En français
- Jean-Paul Delahaye, La complexité mesurée, Pour la Science, n° 314, pp. 34-38, 2003
En anglais
- Rudi Cilibrasi et Paul Vitanyi, Clustering by compression, in IEEE Transactions on Information Theory, vol. 51, n° 4, pp. 1523-1545, 2005 ; voir le document en accès libre (PDF, 328 Ko)
- Ming Li, Xin Chen, Xin Li, Bin Ma et Paul Vitanyi, The similarity Metrics, in Proc. 14th ACM-SIAM Symposium on Discrete Algorithms, 2003
- Rudi Cilibrasi, Paul Vitanyi et R. de Wolf, Algorithmic Clustering of Music, 2003
- Jean-Stéphane Varré, Jean-Paul Delahaye et Éric Rivals, The transformation Distance : a Dissimilarity Measure Based on Movements of Segments, in Bioinformatics, vol. 15, n° 3, pp. 194-202, 1999
- C. Bennett, P. Gacs, Ming Li, P. Vitanyi et W. Zurek, Information Distance, in IEEE Transactions on Information Theory, 44 : 4, pp. 1407-1423, 1998
Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°317, en mars 2004.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).