Le prototypage virtuel à l’échelle atomique
L’ordinateur est depuis longtemps un outil essentiel de l’ingénierie. Au 20e siècle, le développement de l’ingénierie macroscopique a été largement accompagné et stimulé par les progrès des méthodes de conception et de prototypage assistés par ordinateur. Dans l’industrie automobile, par exemple, les voitures sont désormais en grande partie conçues et testées sur ordinateur. Les maquettes numériques remplacent progressivement les maquettes réelles, et le prototypage réel laisse la place au prototypage virtuel, contribuant à la diminution des coûts et des durées de production.
Révolution à l’échelle de l’atome

En février 2007, une « nano-roue » fait la couverture de Nature Nanotechnology.
Qu’en est-il à l’échelle atomique ? En février 2007, on pouvait voir en couverture de Nature Nanotechnology une « nano-roue », constituée de quelques atomes seulement. Pour la première fois, des chercheurs étaient parvenus à faire rouler une telle nano-roue, démontrant ainsi la possibilité d’obtenir un mouvement de rotation contrôlé sur une surface. Cette première mondiale, fruit d’une collaboration entre l’Institut de Physique Expérimentale à Berlin et le CEMES à Toulouse, ouvre la voie à la manipulation de nano-mécanismes plus compliqués, telle la « nano-brouette » conçue au CEMES. Les recherches visent à reproduire au niveau moléculaire le comportement mécanique d’une brouette, c’est-à-dire transformer un mouvement de translation appliqué à la molécule en un mouvement de rotation des nano-roues.
De telles expériences se multiplient, même si le contrôle de la matière à l’échelle de l’atome en est encore à ses balbutiements. À l’université de Caltech, par exemple, Paul Rothemund a montré qu’il est possible de positionner des brins d’ADN afin de dessiner des « smileys » ou tout autre motif. À l’université de Pittsburgh, Chris Schafmeister utilise des acides aminés modifiés pour construire des nano-structures complexes.
Dans chacun de ces exemples, l’ordinateur a joué un rôle important dans la conception des nano-objets. Ainsi, les nano-roues ont d’abord été simulées en résolvant des équations de mécanique quantique par ordinateur. Les séquences des brins d’ADN ont, quant à elles, été déterminées automatiquement par des programmes conçus pour reproduire des motifs spécifiés par les chercheurs. Enfin, les nano-structures à base d’acides aminés modifiés ont été calculées par un programme optimisant des critères de stabilité.

L’expérience de Paul Rothemund. Dans cette expérience, les chercheurs ont d’abord dessiné plusieurs motifs (première rangée : des rectangles, étoiles, « smileys »…). Des ordinateurs ont ensuite déterminé automatiquement la séquence des brins d’ADN (par exemple : ACGGCGTT…) pour que ceux-ci se replient selon les formes souhaitées par les chercheurs (deuxième et troisième rangées).
Ces expériences sont les prémices de ce qu’on appelle la révolution nanobiotechnologique, qui reposera vraisemblablement, comme l’ingénierie, sur le développement de méthodes sophistiquées et générales pour le prototypage virtuel, cette fois à l’échelle atomique. Pour la conception rationnelle de médicaments, la compréhension des mécanismes biologiques est essentielle, et la simulation est déjà couramment employée pour tenter de trouver rapidement les molécules les plus efficaces. De la même façon, l’ordinateur aura un rôle majeur à jouer dans le développement des nanobiotechnologies, en rendant possible une conception et une analyse rationnelle des nano-objets, qu’il s’agisse de molécules inorganiques (comme les nano-roues artificielles) ou organiques (comme les protéines du corps humain).
Comme pour l’ingénierie classique, cependant, des efforts de recherche importants seront encore nécessaires pour concevoir des méthodes de calcul efficaces, en particulier pour simuler le comportement de ces nano-objets.
La simulation dynamique moléculaire
Calculer l’évolution d’une ou plusieurs molécules est en effet un problème difficile, qui est encore le sujet d’intenses recherches.
De manière générale, on appelle simulation dynamique moléculaire un calcul de l’évolution d’un ensemble de molécules au cours du temps. Avant de simuler un ensemble de molécules, il est donc nécessaire de le modéliser, c’est-à-dire de choisir un ensemble de paramètres qui décrivent l’état du système (par exemple, en mécanique newtonienne, les positions et les vitesses des atomes) ainsi qu’un ensemble de lois qui régissent l’évolution de cet état (les forces inter-atomiques, ainsi que leur effet sur le mouvement des atomes). C’est seulement une fois le modèle choisi que l’on peut essayer de déterminer l’évolution de l’état du système au cours du temps.
Parce qu’il n’est généralement pas possible de déterminer analytiquement une fonction qui donne l’état du système pour tout instant t, on emploie dans la plupart des cas une approche numérique, qui consiste à calculer une approximation de cet état, à des instants successifs t0, t1, t2, etc. Le temps total requis pour effectuer une simulation est donc égal au produit du temps moyen passé à effectuer un pas de simulation par le nombre de pas de simulation.
Le temps moyen du calcul d’un pas de simulation dépend essentiellement de deux facteurs : le nombre de variables utilisées pour décrire l’état du système, et la complexité du modèle physique sous-jacent (par exemple, la mécanique newtonienne ou la mécanique quantique).
Quant au nombre de pas de simulation, il dépend directement de la durée du phénomène que l’on souhaite simuler. En raison de la nature des interactions inter-atomiques, il est souvent nécessaire d’utiliser un très petit pas de temps (la durée qui sépare deux instants successifs ti et t(i + 1)). Typiquement, les pas de temps employés sont ainsi de l’ordre de la femtoseconde (10-15 secondes : un millionième de milliardième de seconde). Pour simuler un phénomène qui dure une nanoseconde (10-9 secondes : un milliardième de seconde), il faut donc effectuer un million d’étapes ! Si chaque étape requiert une seconde de calcul sur un ordinateur, la simulation totale prendrait donc un million de secondes, soit un peu plus de onze jours !
Il s’avère donc indispensable de réduire les temps de calcul. Pour cela, deux approches sont habituellement employées.
L’union fait la force
La première approche consiste à augmenter la puissance de calcul. Les chercheurs et ingénieurs construisent ainsi des ordinateurs plus rapides, et développent des algorithmes adaptés. Par exemple, l’ordinateur qui est actuellement le plus rapide du monde, IBM BlueGene/L, est capable d’effectuer un peu plus de 280 000 milliards d’opérations (comme des additions ou des multiplications) par seconde, soit environ 50 000 fois plus qu’un ordinateur grand public.
Une autre façon d’augmenter la puissance de calcul est de relier entre eux des ordinateurs de puissance faible ou moyenne, par internet, afin de combiner leurs puissances de calcul. C’est la méthode choisie par le projet Folding@home de l’université de Stanford, qui utilise le calcul distribué pour prédire la structure des protéines.
En raison du nombre important de processeurs requis, cette approche est donc généralement coûteuse (même si le coût est réparti, dans le cas du calcul distribué).
Simplifions, simplifions
La deuxième approche consiste à simplifier les modèles de molécules employés. Ainsi, un moyen simple de réduire le nombre de paramètres consiste à regrouper des atomes dans un ensemble rigide. Les atomes du groupe rigide ne peuvent alors plus se déplacer indépendamment, et leur mouvement est entièrement décrit par six paramètres : trois en translation et trois en rotation.
Plus généralement, les modèles simplifiés utilisent un petit nombre de coordonnées réduites, définies a priori, dont on pense qu’elles suffiront à reproduire les états que l’on souhaite observer. De par leur nombre réduit, les coordonnées réduites permettent d’accélérer significativement la simulation dynamique. Cependant, la réduction du nombre de paramètres fait qu’il devient impossible de reproduire toutes les configurations que la molécule peut prendre. Dès lors, il n’est pas garanti que les détails intéressants d’un point de vue physique ou biologique seront préservés. Le même problème survient si l’on essaye de simplifier a priori les modèles d’interactions entre les atomes (par exemple, les forces inter-atomiques en mécanique newtonienne).
Simulation adaptative
Afin d’éviter les problèmes liés aux deux premières approches (un coût trop élevé, une simplification peut-être abusive), une troisième approche consiste à déterminer automatiquement, et rigoureusement, où et quand il est possible de simplifier la simulation. Une telle approche est dite adaptative, puisqu’elle permet d’adapter les moyens de calcul à la solution recherchée, en concentrant les efforts sur les phénomènes importants.
Les travaux récents sur la simulation adaptative en angles de torsion, que nous présentons ici, sont issus d’une collaboration avec Serge Crouzy, biophysicien au CEA, au cours du projet AMUSIBIO financé dans le programme Masse de données : Modélisation, Simulation, Applications 2005 de l’Agence Nationale de la Recherche.
C’est tordant !
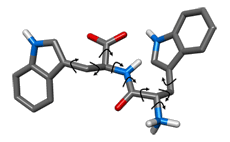
Sur cette molécule, neuf rotations sont possibles, quantifiées par neuf angles de torsion.
Un moyen de modéliser une molécule consiste à considérer que les distances entre atomes contigus sont fixées, et que la molécule peut changer de configuration par rotation autour des liaisons atomiques. Par exemple, la figure ci-contre montre une molécule appelée di-tryptophane (le tryptophane est l’un des vingt acides aminés constituant les protéines), et les neuf rotations possibles, quantifiées par neuf angles de torsion.
Afin de simuler le mouvement d’une molécule modélisée de cette façon, il est donc nécessaire et suffisant de calculer l’évolution des angles de torsion au cours du temps. Plus précisément, il nous faut calculer les accélérations des angles de torsion (c’est-à-dire en langage mathématique, leurs dérivées secondes par rapport au temps).
Un peu d’ordre
Puisque nous souhaitons simuler des molécules de façon adaptative, il nous faut un moyen simple d’accroître ou de réduire la précision de la simulation. Pour cela, nous allons utiliser une représentation hiérarchique d’une molécule : une représentation par assemblages successifs. Dans cette représentation, une molécule est définie comme l’assemblage de deux molécules plus petites, reliées par une liaison. Les deux molécules peuvent tourner l’une par rapport à l’autre, et l’opération d’assemblage est donc associée à un angle de torsion.
L’ensemble des opérations d’assemblage peut être représenté par un arbre d’assemblage binaire, où chaque nœud de l’arbre possède soit deux descendants, soit zéro. Dans cet arbre, les feuilles (c’est-à-dire les nœuds sans descendants) représentent les objets rigides, et la racine (le seul nœud qui n’a pas de parent) représente l’objet articulé tout entier. Par ailleurs, tous les nœuds qui ont des descendants représentent également une articulation : l’articulation utilisée pour assembler leurs descendants. La figure suivante montre comment l’assemblage d’une petite molécule comportant sept articulations peut être construit.
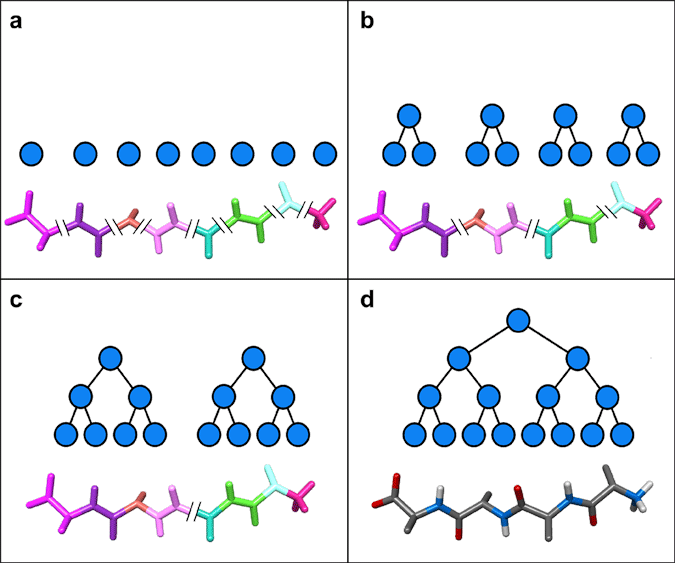
En (a), les huit molécules rigides forment les feuilles de l’arbre. En (b), quatre paires de molécules rigides sont formées. En (c), ces quatre paires sont elles-mêmes regroupées deux à deux pour former deux molécules plus complexes. Finalement, en (d), les deux molécules intermédiaires sont assemblées pour former la molécule complète.
Une telle procédure est générale, et peut s’appliquer à toute molécule.
Travaillons moins, mais travaillons bien !
En représentant une molécule de cette façon, il est possible de simplifier sa dynamique très facilement, en ne simulant qu’une partie des articulations, et en considérant que les autres ne bougent pas.
Bien sûr, la difficulté consiste à déterminer les articulations les plus appropriées, à chaque pas de simulation, afin d’obtenir une bonne approximation du mouvement que l’on aurait obtenu si la simulation n’avait pas été simplifiée.
Puisque nous cherchons à calculer les accélérations angulaires des articulations, une simplification possible est de ne pas calculer les accélérations les plus petites, et de se concentrer sur les accélérations les plus grandes. Bien sûr, ceci semble paradoxal : comment savoir qu’une accélération sera petite sans la calculer ? Surtout, comment éviter d’examiner toutes les articulations, l’une après l’autre, pour conclure peut-être que celles-ci n’étaient pas importantes ?
S’il vous plaît, l’addition !
L’astuce consiste à calculer une grandeur agrégée, qui regroupe plusieurs nœuds. Ainsi, il est possible de montrer que, pour un sous-arbre quelconque (rappelons qu’un sous-arbre représente une partie de la molécule), la somme des carrés des accélérations des articulations du sous-arbre peut être calculée avant de déterminer chacune des accélérations séparément (nous ne démontrons pas ce résultat ici).
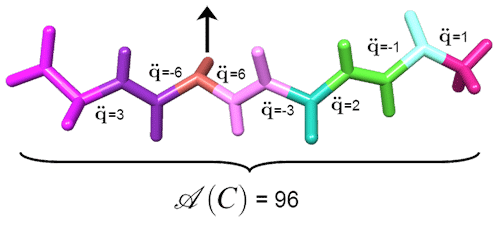
Sur cet exemple, la somme des carrés des accélérations est égale à 96.
Afin de montrer comment ceci nous permet de déterminer les accélérations importantes, reprenons l’exemple de la petite molécule, et imaginons qu’une force soit appliquée à l’endroit indiqué par la flèche sur la figure. Cette force peut être causée par une autre molécule, ou bien par un utilisateur qui souhaite modifier la structure de la molécule (en utilisant sa souris, par exemple). Supposons que les accélérations des angles de torsion soient celles indiquées sur la figure (de gauche à droite : 3, -6, 6, etc.). Alors, la somme A des carrés des accélérations est égale à 96 (en effet, 3×3 + (-6)x(-6) + 6×6 +… = 96). Rappelons que nous sommes capables de calculer la valeur de A sans calculer les accélérations.
Supposons enfin que nous ne voulions calculer que trois accélérations, pour gagner du temps. La figure suivante détaille le processus de sélection des articulations.
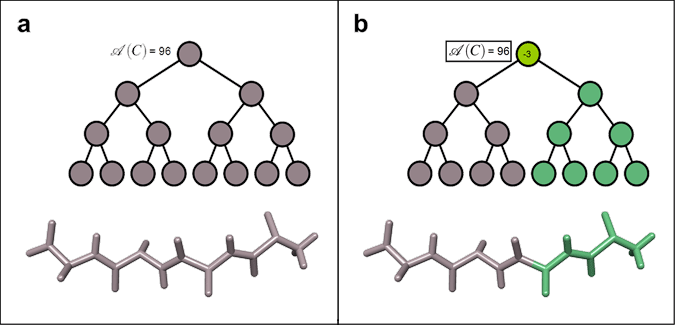
En (a), aucune accélération n’a été calculée (mais nous connaissons déjà la somme A=96). Puisque nous avons le droit de calculer trois accélérations, nous calculons celle du nœud racine, et nous obtenons -3 (partie (b)). La molécule est alors scindée en deux parties rigides, reliées par une articulation active.
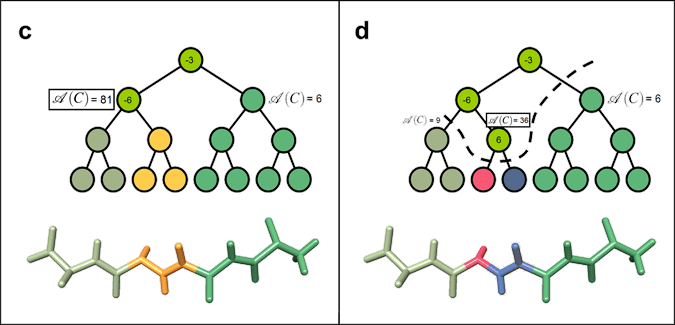
Nous calculons maintenant les sommes associées aux deux nœuds fils du nœud dont nous venons de calculer l’accélération, et nous trouvons 81 pour le nœud gauche, et 6 pour le nœud droit. Le fait que la somme de gauche est plus élevée est la conséquence directe de la présence d’accélérations plus grandes dans la partie gauche de la molécule (3, -6 et 6 à gauche, contre 2, -1 et 1 à droite). Nous choisissons donc de calculer l’accélération du fils gauche, et obtenons -6 (partie (c)).
À ce stade du calcul, la molécule est scindée en trois blocs rigides, et nous avons le droit de calculer encore une accélération. Comme précédemment, nous calculons les deux sommes associées aux nœuds fils du nœud que nous venons de traverser, et obtenons 9 pour le nœud gauche et 36 pour le nœud droit. Nous avons maintenant le choix parmi trois nœuds, dont nous connaissons les sommes A : 9, 36 et 6. Nous choisissons celui avec la somme la plus grande, et calculons l’accélération qui lui est associée : 6 (partie (d)).
La molécule est maintenant scindée en quatre blocs rigides, et nous arrêtons le processus puisque nous ne sommes pas autorisés à calculer plus d’accélérations. Heureusement, les sommes A nous ont bien permis de concentrer les calculs sur les parties les plus mobiles de la molécule à cet instant de la simulation.
Conception et analyse de molécules complexes
Parce qu’elle concentre les calculs sur les régions importantes de la simulation, la méthode adaptative présentée ci-dessus permet de modifier des molécules complexes de façon interactive sur un ordinateur courant. Voici quelques exemples obtenus sur un ordinateur portable muni d’un processeur Pentium 1.7GHz.
De l’hélice alpha au pli bêta
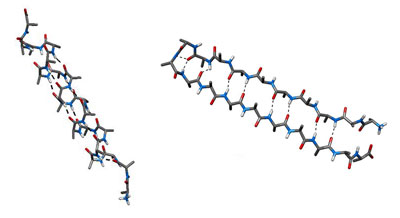
Hélice alpha (à gauche) et pli bêta (à droite).
L’hélice alpha et le pli bêta sont deux motifs très communs dans les protéines. Ici, un utilisateur transforme une hélice alpha en un pli bêta à l’aide de la souris. Le simulateur aide l’utilisateur à construire la nouvelle structure, stabilisée par les forces inter-atomiques.

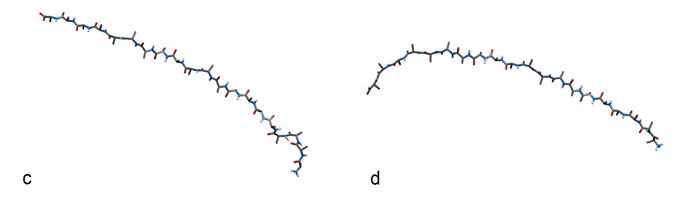
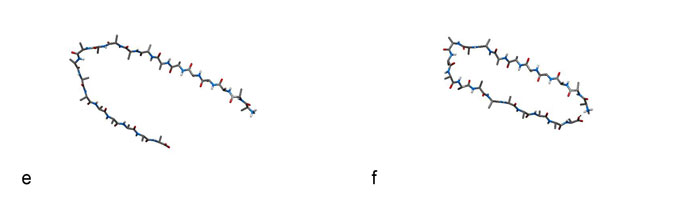
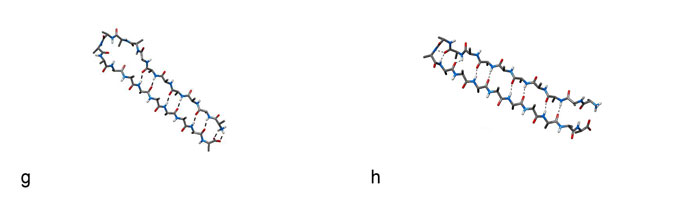
Quelques étapes de la transformation interactive de l’hélice alpha en pli bêta.
L’utilisateur déroule l’hélice en tirant sur la partie supérieure (a-c), puis forme le pli bêta en rapprochant les deux extrémités de la molécule (d-f). Des ajustements locaux, facilités par la simulation interactive, terminent la construction du pli bêta (g-h).
Visionner une séquence vidéo – Durée : 2 min 36 s.
Modification adaptative de structure
Ce deuxième exemple montre l’adaptation automatique de la simulation au cours du temps, en fonction des actions de l’utilisateur. Celui-ci édite un modèle de protéine qui contient 895 atomes et 256 angles de torsion, pour lequel il a autorisé seulement vingt torsions simultanées. La figure suivante montre comment le simulateur adaptatif met à jour l’ensemble des articulations actives au cours du temps.
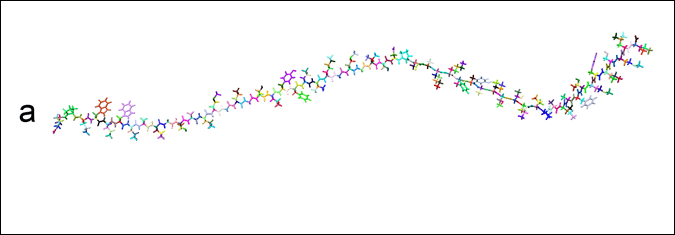
En (a), avant toute modification, toutes les articulations sont actives, et les 257 objets rigides sont visibles (une couleur par objet).
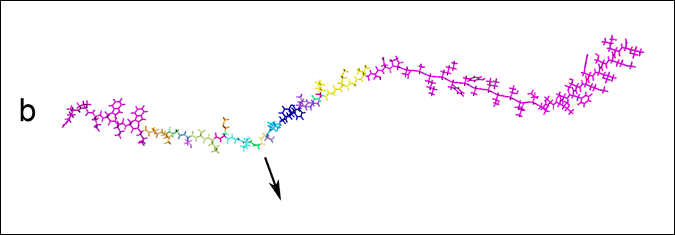
En (b), l’utilisateur applique une force (indiquée par une flèche), en n’autorisant que vingt torsions simultanées, pour permettre une performance interactive sur l’ordinateur portable. Le simulateur adaptatif détermine l’ensemble d’articulations actives le plus approprié, afin d’obtenir une bonne approximation du mouvement qui aurait été obtenu si tous les degrés de liberté avaient été actifs.
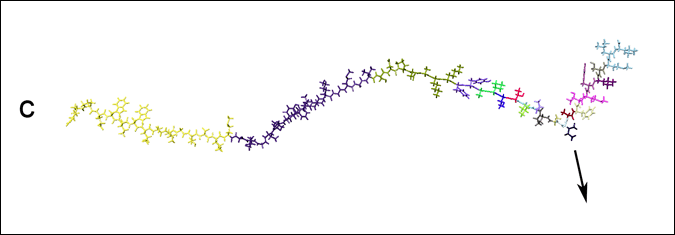
En (c), l’utilisateur applique une force à une autre partie de la protéine, et l’ensemble simulé est adapté automatiquement.
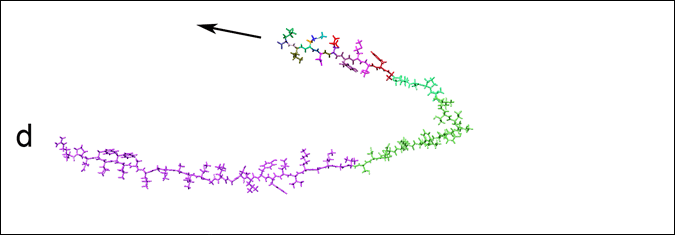
En (d), l’utilisateur déplace une des extrémités de la structure.

Enfin, en (e), lorsque l’extrémité tirée par l’utilisateur se rapproche d’une région précédemment rigide, le simulateur adaptatif la dé-rigidifie automatiquement, pour mieux tenir compte de l’action des forces inter-atomiques.
Visionner une séquence vidéo – Durée : 1 min 45 s.
Modification interactive d’une structure de protéase du VIH
Cet exemple montre comment le simulateur adaptatif permet de modifier simplement une structure de protéase du virus VIH (le virus qui cause le SIDA), afin d’aider à la compréhension de son mécanisme.
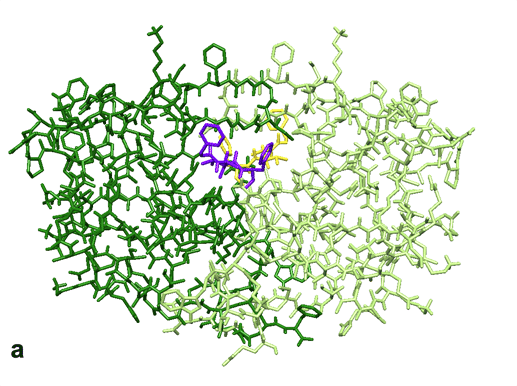
En (a), la structure initiale de la protéase, formée de deux dimères (les deux molécules symétriques les plus grandes), entre lesquels sont placés deux inhibiteurs (les deux petites molécules).
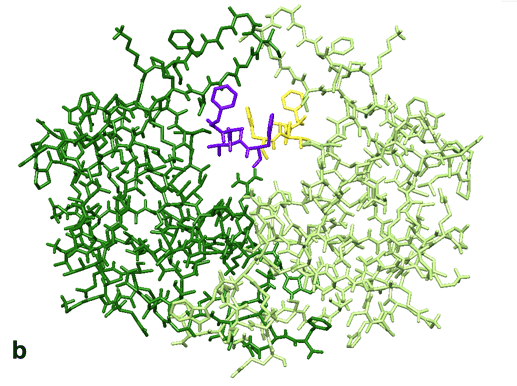
En (b), la nouvelle structure, obtenue par l’utilisateur en quelques « clics » de souris, qui suggère un chemin possible pour l’accès des inhibiteurs au site actif de la protéase.
Perspectives
Comme pour la conception d’objets macroscopiques, de matériaux, de médicaments, ou de composants électroniques, l’ordinateur va jouer un rôle essentiel dans le développement des nanobiotechnologies. L’expérimentation virtuelle, en contribuant à la compréhension des phénomènes physiques, chimiques et biologiques, rendra en effet possible la conception rationnelle de nano-objets sophistiqués.
On l’a vu, le développement de méthodes de prototypage virtuel à l’échelle atomique pose toutefois des problèmes difficiles, en particulier de modélisation et de simulation efficaces.
Einstein, en parlant de recherche en physique, affirmait qu’il fallait « rendre les choses aussi simples que possible, mais pas plus simples ». Puisqu’il faut reproduire fidèlement, sur un ordinateur, des phénomènes complexes en un temps raisonnable, il est nécessaire de simplifier autant que possible – mais pas plus – les modèles et les simulations associées.
Ceci suppose des efforts de recherche multidisciplinaires. Ainsi, en physique, chimie et biologie, il est nécessaire de développer des modèles suffisamment simplifiés pour être calculables. Les enjeux sont si considérables que Walter Kohn, par exemple, a obtenu le prix Nobel de Chimie en 1998 pour ses travaux sur la simplification des équations de la mécanique quantique. En mathématiques, il faut développer, en plus des outils d’analyse de modèles, des méthodes générales de simplification (telle la méthode de décomposition en ondelettes). Enfin, en informatique, il faut concevoir des algorithmes de simulation efficaces, adaptatifs, qui organisent et optimisent les étapes du calcul tout en offrant des garanties sur la qualité de la simulation.
À n’en pas douter, le développement du prototypage virtuel à l’échelle atomique sera, comme les nanobiotechnologies, le fruit d’une collaboration passionnante entre chercheurs en informatique, mathématiques, physique, chimie et biologie.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
