Le hachage
Il était une fois un petit lapin, ou peut-être une hase…

Le hachage se dit Hashing en anglais, tandis que le petit lapin se nomme Häschen en allemand, la langue originale de ce texte. Quant à la hase, en français, c’est la femelle du lièvre.
Mais ce n’est pas seulement pour faire ce jeu de mot multilingue que l’auteur a choisi de vous proposer – et non poser – un lapin !
Il n’est pas facile de trouver un lapin. Cet animal de nature farouche sait bien se cacher. Si vous traversez un champ enneigé et que vous êtes suffisamment attentif, vous pourrez peut-être trouver des traces comme celles-ci :

Ici, ce sont deux lapins qui ont gambadé côte à côte dans la neige. Une telle empreinte peut nous en apprendre long sur l’animal : sa taille, son poids, s’il se déplace seul ou en groupe, etc.
Quelquefois, on peut également trouver cet autre genre de traces :

Dans le jargon des chasseurs, cela s’appelle les laissées. Il s’agit en fait des excréments du lapin. Les laissées permettent de savoir ce que l’animal a mangé, ou s’il est malade. Aujourd’hui, il est même possible d’identifier un animal en analysant en laboratoire l’ADN contenu dans ses excréments. Cela fonctionne pour toutes les espèces animales (en Espagne, on prévoit ainsi de retrouver les chiens « crotteurs de trouble » sur la voie publique).
Passer les fichiers à la moulinette
Qu’est-ce que tout cela a à voir avec un algorithme de hachage ? C’est simple, le hachage a quelque chose à voir avec la digestion. Le lapin mange et dépose ses laissées comme ça :

C’est-à-dire que la nourriture est mâchée, mélangée, digérée, asséchée et rejetée. Il en résulte un petit tas, et ce résultat peut être attribué à une donnée d’entrée, la nourriture. Bien sûr, de nombreuses informations ont été perdues en route, mais il est toujours possible d’établir un lien.
Il en va de même pour les documents numériques, qu’il s’agisse de texte, de musique ou de films. Pour un informaticien, ces fichiers ne sont qu’une succession de zéros et de uns. Le document d’origine est donc mélangé, brassé et comprimé par une série d’opérations jusqu’à obtenir une séquence binaire de longueur définie. Cela ressemble à peu près à ceci :
L’algorithme le plus connu qui exécute cette procédure s’appelle MD-5 (Message Digest 5), ce qui signifie littéralement « condensé de message version 5 ». Il a été développé en 1991 par Ronald Rivest, et Wikipedia en fournit une description détaillée. Les autres algorithmes connus sont SHA-1, SHA-224, SHA-256, SHA-384 et SHA-512. Il s’agit littéralement d’« algorithmes de hachage sécurisés » (Secure Hash Algorithms) qui remplissent les mêmes fonctions de hachage.
Hachage sécurisé
Que font ces algorithmes de hachage ? Tout d’abord, ils condensent des fichiers de longueur différente en séquences binaires de longueur fixe. Ensuite, ils permettent d’identifier le fichier d’origine à partir du résultat obtenu, mais pas de le reconstituer. Formulons ces deux premières propriétés sous forme mathématique :
Nous désignons par {0,1}* l’ensemble de toutes les séquences binaires, soit {0, 1, 00, 01, 10, 11, 000, 001, 010…} et également la séquence vide. Nous désignons par {0,1}k l’ensemble de toutes les séquences binaires comportant exactement k bits, soit : {0..00, 0..01, 0..10, … , 1..11}. Une fonction de hachage f est donc une application :
f : {0,1}* → {0,1}k
Que signifie le fait que le résultat d’une fonction de hachage permette d’identifier clairement le fichier d’origine ? Cela signifie que f(x) = f(y) sera vrai si et seulement si x = y.
Le contraire de cette affirmation s’exprime par : il existe deux valeurs x et y différentes telles que f(x) = f(y). Si deux valeurs distinctes ont la même image, alors à partir de cette image, on sera incapable de déterminer la valeur d’origine. Ce type de conflit s’appelle une collision.
Nous affirmons donc qu’il existe une fonction de hachage sans collision pour toutes les séquences binaires. D’un point de vue mathématique, cette affirmation est absolument aberrante. Pourquoi ?
Imaginons que chaque valeur de hachage soit un tiroir ; nous avons donc autant de tiroirs qu’il existe de séquences binaires de longueur k, c’est-à-dire 2k, ce qui correspond à 2 possibilités pour chaque bit. Nous affirmons donc qu’il est possible de ranger dans chacun de ces tiroirs f(x) une seule séquence binaire originale. Mais ces séquences existent en nombre infini, donc supérieur à 2k. Au moins l’un de ces tiroirs doit donc contenir un nombre infini de valeurs d’origine, et ce tiroir-là présente alors un nombre infini de collisions.
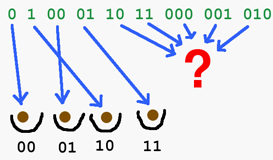
Mais il existe une sortie de secours. Nous choisirons une valeur de k assez grande pour avoir un nombre de tiroirs suffisant pour qu’à chaque fichier enregistré sur un ordinateur puisse être attribué au moins une valeur de hachage. Cela se rapproche du principe des fonctions à sens unique utilisées pour la cryptographie à clé publique. Si nous prenons par exemple k = 512, nous obtenons 2512 soit plus de 10154 tiroirs. Si nous arrivons à remplir ces tiroirs sans que quiconque (homme ou machine) ne parvienne à établir une collision, alors nous sommes sortis de l’auberge.
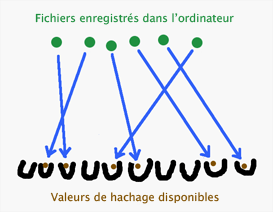
Personne ne sait encore si cela peut fonctionner. Certes, il existe déjà quelques prétendants à ce titre, comme SHA-512 (dont la valeur de hachage est de 512 bits), mais cela ne veut pas dire grand chose. Ainsi, MD-5 a longtemps été réputé pour ne présenter quasiment aucune collision, alors qu’on connaît aujourd’hui des méthodes permettant de générer autant de collisions qu’on le souhaite.
Les fonctions de hachage sans collision sont très utiles en informatique. Elles permettent par exemple de vérifier l’intégrité de fichiers au moyen d’une valeur de hachage transmise avec le fichier et de détecter ainsi les éventuelles erreurs de transmission ou tentatives de falsification.
Hachage pour les dictionnaires
Outre l’identification de fichiers, les fonctions de hachage représentent également un moyen efficace de stockage des données. Imaginons que nous disposions d’un espace de mémoire S pour stocker une quantité m de données. Cette mémoire est organisée en tableau (ou array). Il est donc possible d’accéder directement à chaque valeur stockée S[1], …, S[m].
À présent, enregistrons dans cette mémoire des données que nous pourrons identifier à partir d’une séquence binaire (ou de caractères) qui servira de clé.
Par exemple :
| lapin | 12 |
| renard | 2 |
| hérisson | 4 |
| ours | 1 |
Les données sont très compactes, tandis que l’index de recherche est très long. Supposons que nous ayons une fonction de hachage f qui applique les séquences de caractères à l’intervalle {1,2,3,..,m}, soit
f : {a,b,…,z}* → {1,2,…,m}
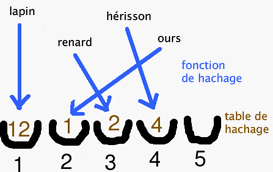
Nous pourrions alors insérer la valeur 12 dans la cellule S[f(« lapin »)], la valeur 2 dans la cellule S[f(« renard »)], et ainsi de suite… Nous appelons cette opération Put (insérer).
Put (string x, int z)
begin
S[f(x)] := z
end
Get permet de retrouver la valeur, la valeur 0 indiquant qu’aucun fichier n’est enregistré.
Get (string x)
begin
return S[f(x)]
end
Malheureusement, ces deux fonctions ne marchent que si l’algorithme de hachage ne présente absolument aucune collision, c’est-à-dire si par exemple le lapin et le hérisson ne sont pas envoyés dans la même cellule. Cela ne peut être garanti pour de petites valeurs de m que si l’on connaît déjà la clé (ici lapin, renard, hérisson et ours) et que l’on choisit une fonction de hachage parfaite.
Gestion des collisions
En présence de collisions, il faut trouver une cellule libre. Pour cela, il existe plusieurs méthodes, dont la plus simple est appelée sondage linéaire. Elle nécessite d’enregistrer dans chaque cellule du tableau la clé avec la donnée.
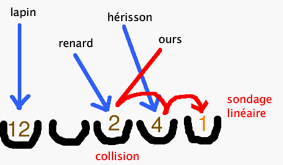
- Enregistrement de la donnée z sous la clé x :
On calcule tout d’abord la valeur de hachage de x. Si la cellule correspondante est déjà occupée par une autre clé, on poursuit alors vers la droite jusqu’à trouver une cellule vide ou une cellule comportant la clé recherchée. Une fois arrivé au bout, on revient à la première cellule et on continue le sondage. Une fois trouvée la cellule avec la clé recherchée ou une cellule libre, on y insère la clé x et la donnée z. Si la recherche n’a donné aucun résultat, alors la mémoire est pleine et on obtient un message d’erreur.
- Recherche de la donnée sous la clé x :
Encore une fois, on calcule tout d’abord la valeur de hachage f(x) de x. Si on trouve dans la cellule correspondante une autre clé, on poursuit vers la droite jusqu’à trouver la bonne clé ou une cellule vide. Une fois arrivé au bout, on reprend le sondage depuis le début. La recherche est sans résultat si l’on trouve une cellule vide ou si l’on finit par faire le tour complet du tableau. La recherche aboutit si l’on a trouvé la clé x, on obtient alors la donnée correspondante.
Cette gestion des collisions permet donc toujours de stocker m données, quelle que soit la qualité de la fonction de hachage. Pour l’essayer par vous-même, utilisez comme clé des nombres entiers et comme fonction de hachage la fonction modulo m. Il s’agit du reste de la division euclidienne par m.
Animation interactive
Dans l’animation ci-dessous, choisissez un algorithme de hachage dans le menu déroulant.
5 exemples d’algorithmes modulo n vous sont proposés, ils calculent la valeur des nombres saisis modulo n. Le nombre de cases de la table est égal à n, on peut donc y ranger n nombres.
Le dernier exemple d’algorithme proposé calcule la somme des chiffres puis garde le dernier chiffre du résultat. Cette table comporte 10 cases, 10 nombres peuvent y être rangés.
Au début, l’enregistrement et la recherche seront très rapides. Au fur et à mesure que le tableau se remplit, notre algorithme sera de plus en plus lent.
Cela est dû à la mauvaise gestion des collisions. En effet, le traitement linéaire des collisions effectue sa recherche toujours dans les mêmes cellules. De meilleures solutions existent, comme la méthode quadratique ou le double hachage. Mais nous nous contenterons pour ce document d’un double petit lapin.

Une première version de ce document est parue en allemand dans la série Algorithmus der Woche publiée à l’occasion de l’Année de l’informatique (Informatikjahr) 2006.
Animation HTML5/JS réalisée par Corentin Wallez, XProjets et améliorée par Ouest INSA, à partir d’une applet réalisée par Hamdi Ben Abdallah.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
