
Le patient virtuel au service de la chirurgie
Les images de synthèse envahissent nos écrans. Les personnages virtuels se glissent dans nos téléviseurs, nos cinémas, et bien sûr dans les consoles de jeux. Mais ces enveloppes corporelles calculées par ordinateur ont aussi trouvé dans le domaine de la médecine et de la chirurgie un nouvel espace d’évolution. Et ce ne sont plus des personnages inventés de toutes pièces que l’on trouve en salle d’opération, mais bel et bien une copie virtuelle du patient.
La médecine et la chirurgie ont tout à gagner à mettre à profit ces nouvelles technologies, qui offrent de multiples avantages, à différents stades du parcours médical du patient. Les images numériques peuvent tout d’abord aider au diagnostic. Elles peuvent également aider le praticien à préparer, à planifier un geste chirurgical difficile, à essayer différents scénarios avant l’intervention. Elles peuvent entrer jusqu’à la salle d’opération pour guider le chirurgien pendant son geste. Enfin, elles peuvent permettre à des praticiens novices de s’exercer avant de pratiquer pour la première fois des interventions.
De l’acquisition à la visualisation des images
Le cycle de l’image médicale commence au moment de l’acquisition. Différentes technologies et différents matériels existent depuis plusieurs années, comme le scanner (tomographie par rayons X), l’IRM (résonance magnétique nucléaire), ou l’échographie (ultrasons). Ces techniques produisent le plus souvent comme résultat une série d’images en 2 dimensions, les coupes qui, mises les unes derrière les autres, reconstituent le volume du patient.
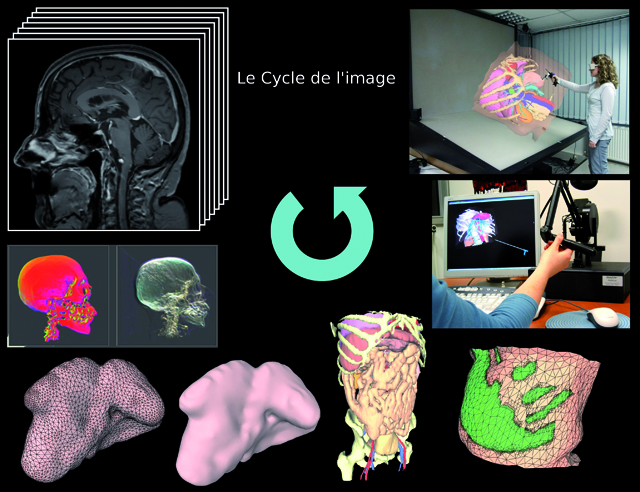
Le cycle de l’image (© LSIIT/données IRCAD)
Le patient virtuel est reconstitué grâce à des calculs et traitements effectués sur les images sources, comme le scanner ou l’IRM que passe le patient réel.
Lorsque le patient passe une IRM ou un scanner, il n’imagine pas les nombreux traitements mathématiques et informatiques que va subir son image afin d’être exploitée par les logiciels utilisés par les chirurgiens. De la simple visualisation aux calculs élaborés permettant d’assister le chirurgien dans son diagnostic ou dans la préparation d’un geste, ou même jusqu’aux simulateurs en réalité virtuelle, le moindre pixel est exploité.
Cette image montre quelques-unes des utilisations de l’image à partir de l’acquisition d’origine (en haut à gauche). L’image peut être visualisée dans sa globalité (visualisation volumique) ou organe par organe : ici des reconstructions de la surface d’une rate, ainsi que l’abdomen entier d’un patient. En bas à droite, un calcul de zones d’intérêt sur une portion de surface de peau. Enfin, des exemples de simulateurs d’insertion d’aiguilles. Le premier utilise un bras à retour d’effort pour ajouter la sensation tactile à la simulation, le deuxième (en haut à droite) s’affiche sur une station de visualisation 3D stéréoscopique pour augmenter le réalisme grâce à un meilleur sentiment d’immersion.
À partir d’une série de coupes, on peut reconstituer ce que l’on appelle une image en 3 dimensions, constituée de voxels. Un voxel (contraction de volumetric pixel) est la plus petite unité de l’image 3D, par analogie avec le pixel (contraction de picture element) qui est l’unité de surface d’une image 2D. Une image en 3 dimensions est donc un parallélépipède constitué d’une grille de voxels, dont chacun possède un attribut de niveau de gris. À ce stade, il est impossible de visualiser ce volume d’image tel quel, car des voxels opaques des faces extérieures du parallélépipède masqueraient les voxels internes.
Pour le visualiser, la première possibilité est d’utiliser le rendu volumique, qui consiste à visualiser directement la grille de voxels par transparence. L’ordinateur « lance des rayons » dans l’image, et affecte à chacun une couleur qui sera affichée à l’écran en fonction du trajet parcouru et des structures rencontrées. Mais cette technique d’affichage est difficile à interpréter, car nous ne sommes pas très habitués à voir diverses couches par transparence.
Comment synthétise-t-on les images ?
Une autre façon de procéder est de calculer des isosurfaces. Ce sont des surfaces tridimensionnelles qui correspondent à un même niveau de gris dans l’image 3D. Chaque structure anatomique possédant son propre niveau de gris, ou une petite plage de niveaux de gris très proches, il est ainsi possible de les différencier en connaissant le niveau de gris leur correspondant. Par exemple, sur des images scanner, les os sont très clairs, ce qui permet de les différencier des organes « mous » qui sont foncés. L’étape qui consiste à « découper », partitionner l’image selon les différentes structures anatomiques d’intérêt, s’appelle la segmentation.
Une fois les structures anatomiques segmentées, on dispose d’une forme en voxels pour chacune d’entre elles. De ces formes pleines peuvent ensuite être extraites des surfaces, constituant en quelque sorte leur enveloppe, plus facile à afficher pour nos ordinateurs. Cette étape nommée reconstruction se fait grâce à des algorithmes, dont le « marching cubes », permettant d’obtenir des surfaces polygonales, qui peuvent ensuite être colorées et éclairées pour un affichage réaliste. Le praticien passe ainsi d’une série d’images 2D en niveaux de gris représentant des « tranches » de patient, à examiner l’une après l’autre, à une véritable représentation en 3D des structures anatomiques. Il est ainsi beaucoup plus facile pour lui de se représenter mentalement les positions relatives de ces structures les unes par rapport aux autres, ainsi que l’emplacement des pathologies et ce qui les entoure.

Foies modélisés (© LSIIT/données IRCAD), vignette d’après William E. Lorensen, Harvey E. Cline. Marching cubes, a high resolution 3D surface construction algorithm, 1987.
L’algorithme des marching cubes a pour objectif de transformer une forme pleine constituée d’un amas de petits cubes, en une surface creuse qui représente son bord.
L’algorithme des marching cubes a pour objectif de transformer une forme pleine constituée d’un amas de petits cubes, en une surface creuse qui représente son bord.
Cet algorithme, publié en 1987 par Lorensen et Cline, consiste à examiner les configurations de voisinage de tous les voxels du bord d’une forme 3D discrétisée (champ scalaire en 3 dimensions), afin de les remplacer par des facettes triangulaires. Les voxels sont examinés par blocs de huit. Quinze configurations possibles de 8 voxels ont été prédéterminées, donnant lieu à 15 configurations possibles de placement d’une ou plusieurs faces triangulaires. Les faces obtenues pour les blocs adjacents sont reliées entre elles par leurs arêtes et leurs sommets pour former une surface complète, qui représente une approximation du champ scalaire. Ces surfaces polygonales peuvent alors être agrémentées d’une couleur ou d’une texture (par exemple à base de photos), de propriétés de réflexion, et éclairées afin d’obtenir une visualisation réaliste. Un des problèmes de cet algorithme est qu’il peut parfois conduire à des surfaces ayant un aspect de « marches d’escalier », mais cela peut être atténué par l’utilisation d’algorithmes de lissage.
Au-delà de la simple visualisation, la synthèse d’images permet une navigation virtuelle à l’intérieur des organes du patient. On peut ainsi, par exemple, naviguer à l’intérieur de l’artère coronaire à la recherche de calcifications (dépôts calcaires sur la paroi interne) pouvant mener à un rétrécissement artériel et au diagnostic de l’imminence d’un infarctus.
La synthèse d’images pour la simulation
Mais la puissance des ordinateurs nous offre encore bien d’autres possibilités. Tout comme les pilotes d’avion disposent de simulateurs de vol pour s’entraîner, on peut élaborer des simulateurs de chirurgie. En plus de permettre l’entraînement sur une copie virtuelle du patient, celui-ci a l’avantage d’être paramétrable, ce qui permet de placer un chirurgien apprenti dans toutes sortes de situations imprévues et soudaines, ou devant des pathologies inhabituelles. De plus, contrairement à un animal ou à un mannequin en plastique par exemple, un patient virtuel a une anatomie humaine complète et réaliste et peut être doté, grâce à des algorithmes de simulation sophistiqués, de fonctions physiques et physiologiques opérationnelles (respiration, battements du cœur, circulation sanguine). Cela permet de reproduire les interactions avec les outils chirurgicaux et les effets de l’intervention, positifs ou négatifs, comme une cautérisation, une incision, ou encore une hémorragie. Les algorithmes de simulation peuvent être classés principalement en 2 catégories : les simulations d’interactions entre objets et les simulations de fluides.
La première catégorie permet par exemple de simuler la déformation d’organes mous lorsque ceux-ci sont touchés par un outil chirurgical. Les maillages, surfaciques ou même volumiques (maillages composés de tétraèdres remplissant leur intérieur), sont déformés en calculant puis en appliquant des déplacements à certains de leurs sommets. Les problèmes qui se posent alors sont : à quel moment des sommets doivent-ils être déformés, quels sommets sont déformés, et comment sont-ils déformés ? Un simulateur temps réel implique que l’ordinateur soit en permanence en train de calculer les positions relatives des objets, et détecte au plus vite une collision lorsqu’elle se produit, ce qui constitue une extraordinaire quantité de calculs à effectuer si les maillages possèdent des milliers de sommets. On utilisera donc des techniques d’accélération de ces calculs. La plus courante consiste à calculer pour chaque maillage sa boîte englobante, qui est le plus petit parallélépipède rectangle aligné sur les axes et contenant tous ses points. Le calcul est alors simplifié : tant qu’il n’y a aucune intersection de parallélépipèdes, ce qui revient à calculer quelques inégalités, alors on est sûr qu’aucun maillage n’est en collision avec un autre. Si deux parallélépipèdes présentent une intersection, alors il y a un risque que leurs deux maillages soient en contact, et il est nécessaire de procéder à un calcul plus approfondi.
Dans ce cas, on doit rechercher quels sommets sont en contact. Là encore, on peut accélérer les calculs, par exemple en utilisant un octree, une indexation spatiale qui consiste à découper l’espace situé dans la boîte englobante en une arborescence de boîtes de plus en plus petites, et à étiqueter chaque sommet du maillage selon sa position. On peut alors définir rapidement quelles sont les boîtes concernées par la collision, et ainsi éviter de faire des calculs sur les points situés dans d’autres boîtes. Lorsqu’on a finalement déterminé quels sommets d’un maillage déformable étaient en collision avec un autre objet, on peut enfin calculer sa déformation. Les sommets en collision directe sont déplacés en suivant la position de l’objet qui les a touchés. Mais la surface, souvent constituée de tissus mous élastiques, subit également une déformation du voisinage de ces sommets. Plus un sommet est éloigné du lieu de la collision, plus sa déformation est atténuée. La déformation est donc définie par une zone d’influence et par une fonction de déformation (gaussienne, B-spline, ou autre). Dans la deuxième catégorie, les simulations d’écoulement de fluides (liquides, gaz) quant à elles n’utilisent généralement pas de maillages, mais simulent plutôt des animations de particules, qui suivent les lois de la mécanique des fluides calculables grâce aux équations de Navier-Stokes. On peut ainsi simuler et visualiser l’écoulement de sang lors d’une hémorragie, ou la production de fumée lors d’une cautérisation.
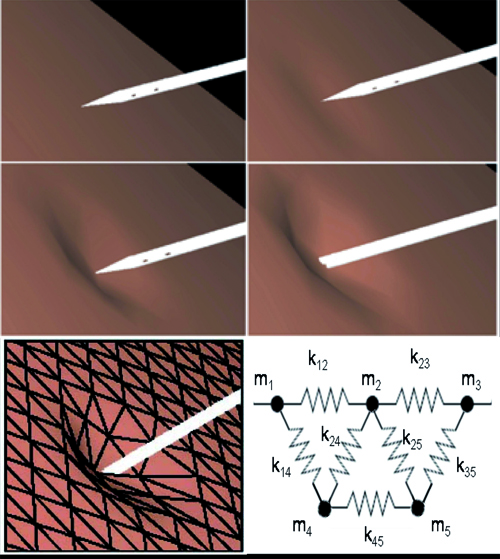
Déformation de maillages (© LSIIT/IRCAD)
La déformation d’un maillage permet de reproduire visuellement le comportement d’un organe mou lors d’un contact avec un outil chirurgical, en tenant compte de ses propriétés d’élasticité.
La déformation de maillages consiste à modifier l’emplacement de certains sommets pour représenter de façon réaliste la réponse d’une surface souple à une collision avec un objet. Les sommets seront plus ou moins déplacés en fonction de leur distance par rapport à l’objet (on parle de zone d’influence). Leur déplacement dépend également de la fonction mathématique, qu’on appelle fonction d’extrusion, choisie pour représenter au mieux les propriétés de la surface déformable. Si la surface possède des propriétés d’élasticité, on peut également utiliser un système masse-ressort pour modéliser la déformation. À chaque sommet, on associe une masse et, à chaque arête, on associe un ressort, dont on connaît la raideur et la longueur au repos. Ainsi, en fonction d’un déplacement appliqué en un point, on peut déterminer quelle sera la répercussion sur chacun des sommets alentour en calculant les forces qui s’exercent sur eux.
La synthèse d’images pour la planification d’interventions
Mais bien souvent, le praticien aimerait aller plus loin que la simulation. En effet, pour préparer son geste opératoire, par exemple définir une voie d’accès pour enlever une tumeur, ou encore définir une trajectoire pour une insertion d’aiguille, même si une simulation peut l’aider à visualiser les éventuels obstacles se situant sur le parcours, il doit encore faire tout un travail d’essais-erreurs jusqu’à trouver le bon angle d’attaque.
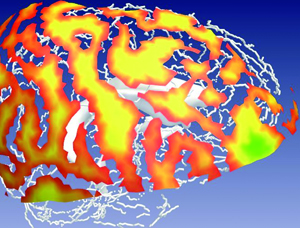
Prédiction de trajectoire en neurochirurgie (© LSIIT/Inria Visages)
Là encore, la géométrie et les mathématiques en général (par des méthodes d’optimisation numérique) peuvent l’aider, en calculant à sa place les zones d’insertion possible avec une estimation de leur qualité (voir photo ci-contre), ainsi que la ou les trajectoires optimales.
Ces algorithmes font intervenir des calculs souvent relativement simples, des intersections droites-triangle dans l’espace, des distances d’un point à un autre ou d’une droite à un triangle, des angles entre deux vecteurs. Ce qui fait la difficulté, c’est encore une fois le très grand nombre de calculs à effectuer en un temps suffisamment raisonnable pour obtenir un résultat rapide. Le chirurgien ne serait pas intéressé par un logiciel qui lui indiquerait en 3 jours un résultat qu’il peut obtenir avec un simulateur en quelques minutes !
L’avenir : réalité virtuelle
L’avenir nous réserve encore bien des améliorations au réalisme des simulations, notamment avec l’utilisation grandissante des dispositifs de réalité virtuelle. On connaît et on maîtrise assez bien désormais les techniques de visualisation 3D stéréoscopique, de plus en plus utilisées au cinéma et bientôt même sur nos téléviseurs, qui permettent de voir en relief. Ces techniques apporteront un plus à la représentation tridimensionnelle de l’anatomie du patient.
On connaît peut-être moins les périphériques à retour d’effort, qui permettent de simuler la sensation de « toucher » des objets. Le principe est simple : quel que soit le type de dispositif (souvent des bras articulés), des moteurs commandés par l’ordinateur bloquent le mouvement d’un effecteur (stylet ou poignée par exemple) en cas de contact avec un objet. Ce blocage est calculé en fonction de la position de l’effecteur par rapport aux positions connues des objets de la scène, et sa rigidité est fonction des paramètres de l’objet touché (dur, mou), qui est éventuellement déformable. Dans le cas de la chirurgie, on peut ainsi obtenir des simulateurs avec retour tactile, en remplaçant l’effecteur par un véritable outil chirurgical comme un scalpel, et qui réagissent comme dans la réalité en répondant au contact avec la peau par une sensation de frottement et de résistance. Les mathématiques et l’informatique joueront donc un rôle de plus en plus important dans cet effort de modélisation multi-échelle et multimodale de patients virtuels, afin de développer les simulateurs les plus réalistes possibles.
Le mot haptique vient du grec « haptein » qui signifie « toucher ». Les interfaces haptiques sont des périphériques qui simulent des sensations de toucher ou kinesthésiques. On distingue deux grandes familles : les interfaces tactiles, qui font ressentir la forme, la texture ou la température sur les capteurs situés au niveau de la peau, et les interfaces à retour d’effort qui permettent de ressentir la position et les mouvements, les forces exercées (collisions, poids, viscosité) grâce aux capteurs proprioceptifs situés dans les muscles et les tendons. Ces derniers sont le plus souvent utilisés dans les simulateurs chirurgicaux, sous la forme de bras articulés munis de moteurs dans leurs articulations. De véritables outils chirurgicaux peuvent être placés au bout de ces bras pour une simulation réaliste.
- Le traité de la réalité virtuelle, volumes 1 à 4, Presses de l’école des Mines de Paris, 2006
- Guide des technologies de l’imagerie médicale et de la radiothérapie : Quand la théorie éclaire la pratique, Jean-Paul Dillenseger et Elisabeth Moerschel, Masson, 2009
- Visible Human Project
Cet article est paru dans la revue DocSciences n°13 Informatique et médecine, éditée par le CRDP de l’Académie de Versailles en partenariat avec l’Inria.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Caroline Essert