Faire une multiplication… plus vite qu’à l’école !
1. La méthode scolaire
Pour multiplier entre eux deux nombres entiers a et b, on multiplie a par chaque chiffre de b et on écrit ces produits intermédiaires en biais les uns au-dessous des autres. Ensuite, on additionne ces produits intermédiaires. Selon les pays, il existe quelques variantes dans la façon de poser les opérations, mais globalement, c’est ainsi que fonctionne la méthode scolaire de la multiplication.
| 5 | 6 | 7 | 8 | ||||
| × | 4 | 3 | 2 | 1 | |||
| 5 | 6 | 7 | 8 | ||||
| 1 | 1 | 3 | 5 | 6 | . | ||
| 1 | 7 | 0 | 3 | 4 | . | . | |
| 2 | 2 | 7 | 1 | 2 | . | . | . |
| 2 | 4 | 5 | 3 | 4 | 6 | 3 | 8 |
Lorsque les nombres a et b sont grands, c’est-à-dire qu’ils comportent beaucoup de chiffres, alors cette méthode devient trop coûteuse en temps. Cela mérite réflexion.
- Pourquoi juge-t-on cette méthode trop coûteuse en temps ?
- Existe-t-il une autre méthode qui nous permettrait de gagner du temps ?
Ces questions sont intéressantes pour plusieurs raisons.
- Du point de vue pratique : effectuer rapidement des calculs sur de grands nombres est utile dans beaucoup de domaines d’application de l’informatique, par exemple, pour manipuler l’information ou pour résoudre efficacement des problèmes géométriques et arithmétiques.
- Du point de vue théorique : la méthode scolaire de la multiplication nous paraît si familière et naturelle que toute amélioration significative – et nous allons en découvrir une – constitue une véritable surprise.
Mais que veut-on dire par « la méthode scolaire est trop coûteuse en temps » ? Les informaticiens ne mesurent pas le temps de calcul en secondes (car l’année prochaine, de nouveaux ordinateurs plus rapides seront disponibles sur le marché), mais en nombre d’opérations de base qu’une méthode réalise. On peut ainsi comparer des algorithmes et pas les ordinateurs sous-jacents. Une opération de base est quelque chose qu’un ordinateur ou un humain peut faire en une seule étape. Les opérations de base dont nous avons besoin ici sont des calculs qui font intervenir des nombres à un seul chiffre en base 10, les nombres étant donc écrits avec les chiffres 0, 1, 2…, 8, 9. Plus précisément, on considère :
- multiplication de deux nombres à un chiffre : si nous connaissons nos tables, nous pouvons pour deux nombres x et y à un chiffre qu’on nous donne, déterminer en une seule étape les deux chiffres u et v de leur produit : x × y = 10 × u + v où u et v n’ont qu’un seul chiffre. Nous appelons cette opération multiplication élémentaire.
Par exemple, pour les nombres x = 3 et y = 7, nous savons que x × y = 3 × 7 = 21 = 2 × 10 + 1, nous obtenons donc les chiffres du résultat u = 2 et v = 1. Pour x = 3 et y = 2, nous avons u = 0 et v = 6 ; - addition de trois nombres à un chiffre : pour trois nombres à un chiffre x, y, z, nous pouvons trouver les deux chiffres de leur total en une étape : x + y + z = 10 × u + v où u et v n’ont qu’un seul chiffre. (Nous verrons juste après la raison pour laquelle nous voulons additionner ici trois nombres à un chiffre plutôt que deux.)
Par exemple, pour x = 3, y = 5 et z = 4, nous avons u = 1 et v = 2, parce que 3 + 5 + 4 = 12 = 1 × 10 + 2.
En ne considérant que ces deux opérations de base, on va comparer des algorithmes de multiplication. Combien d’opérations de base la méthode scolaire de la multiplication nécessite-t-elle alors ? Avant de pouvoir répondre à cette question, nous devons d’abord évoquer l’addition de deux grands nombres, car nous en avons également besoin pour la multiplication.
L’addition de grands nombres
Combien d’opérations faut-il pour additionner deux nombres a et b ? Cela dépend naturellement de leur longueur. Supposons que a et b comportent chacun n chiffres. (Si l’un des deux nombres est plus court, nous ajoutons simplement des zéros devant celui-ci, pour obtenir deux nombres de même longueur.) Pour les additionner, nous les écrivons l’un au-dessous de l’autre et additionnons de droite à gauche les chiffres dans chaque colonne selon la méthode présentée ci-dessus. À partir du résultat 10 × u + v, nous inscrivons le chiffre v comme chiffre du résultat dans la colonne considérée et nous ajoutons le chiffre u comme troisième chiffre (retenue) à la colonne suivante. Voici un exemple avec des nombres à quatre chiffres, donc pour n = 4 :

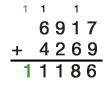
Nous procédons ainsi de droite à gauche pour toutes les n colonnes. Finalement, nous inscrivons la dernière retenue sans autre calcul comme chiffre du résultat le plus à gauche. Nous avons alors effectué au total n opérations de base, à savoir une addition de deux ou trois chiffres pour chaque colonne.
La multiplication d’un grand nombre par un nombre à un chiffre
Revenons à la méthode scolaire de la multiplication. Les produits intermédiaires distincts, écrits chacun sur une ligne, qui apparaissent dans cette méthode, émanent de la multiplication d’un grand nombre a (c’est-à-dire le multiplicande) par un nombre à un seul chiffre y (qui fait partie du multiplicateur). Regardons à présent de plus près cette opération, en détaillant ses résultats intermédiaires un peu plus que d’habitude. Considérons de droite à gauche les chiffres de a. Nous multiplions chaque chiffre x de a par y. Nous écrivons le résultat 10 × u + v sur une nouvelle ligne, de sorte que v se trouve dans la même colonne que x, et u à sa gauche. Ensuite, nous additionnons tous ces résultats intermédiaires à deux chiffres. Cela nous fournit le produit intermédiaire, que nous écrivons habituellement directement sur une seule ligne en mémorisant les retenues. Pour le dernier produit intermédiaire de notre exemple du début, cela se présente ainsi :

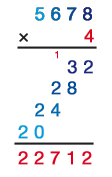
Combien d’opérations de base avons-nous effectuées ? Pour chacun des n chiffres de a, nous avons effectué une multiplication élémentaire. (Dans l’exemple ci-dessus : quatre multiplications élémentaires pour les quatre chiffres du nombre 5678.) Ensuite, nous avons dû additionner les résultats intermédiaires dans n + 1 colonnes. Il n’y a qu’un seul chiffre dans la colonne la plus à droite, nous ne devons donc rien calculer dans celle-ci. Mais dans les autres n colonnes, il y a deux chiffres et éventuellement une retenue de la colonne précédente, de sorte que nous avons besoin d’effectuer une addition de ces chiffres. Cela fait donc n additions. Avec les multiplications élémentaires, cela fait au total 2 n opérations de base pour la « multiplication d’un nombre à n chiffres par un nombre à un chiffre » (ou n additions et n multiplications).
Analyse de la méthode scolaire de la multiplication
Analysons à présent le nombre d’opérations de base que nécessite la méthode scolaire de la multiplication pour deux grands nombres a et b, qui comportent n chiffres. (Comme avant, si l’un des nombres est plus court, nous écrivons suffisamment de zéros.)
Pour chaque chiffre y de b, nous devons calculer un produit intermédiaire a × y. C’est une « multiplication d’un grand nombre par un nombre à un chiffre », elle nécessite donc 2 n opérations de base, tel qu’expliqué ci-dessus. Comme b possède au total n chiffres, nous devons effectuer n × (2 × n) = 2 × n2 opérations de base, pour calculer tous les produits intermédiaires.


Ensuite, nous devons additionner les produits intermédiaires, placés en biais les uns au-dessous des autres. Pour nous simplifier le calcul, pensons à inscrire des zéros aux endroits vides ; nous obtenons alors n nombres de la même longueur, que nous devons tous additionner. À cette fin, nous utilisons plusieurs fois la méthode décrite ci-dessus pour l’addition des grands nombres : nous additionnons d’abord la première ligne avec la deuxième, puis nous additionnons la troisième ligne avec ce sous-total, et ainsi de suite, jusqu’à ce que nous ayons finalement additionné tous les n produits intermédiaires. Nous avons donc besoin de n − 1 additions de grands nombres. (Dans l’exemple, avec n = 4, nous avons besoin de trois additions pour faire le total des quatre produits intermédiaires, c’est-à-dire : 5678 + 113560 = 119238, 119238 + 1703400 = 1822638 et 1822638 + 22712000 = 24534638.)
Mais combien d’opérations de base cela fait-il ? Pour être en mesure de le dire, nous devons connaître la longueur de tous les sous-totaux qui apparaissent pendant cette série d’additions. Changeons de perspective : le résultat final de notre calcul, a × b, peut au plus avoir 2 n chiffres. (Si vous ne voyez pas pourquoi, réfléchissez-y !) Au fur et à mesure que nous additionnons les lignes les unes après les autres, les nombres deviennent toujours plus grands, ils ne redeviennent jamais plus petits. Par conséquent, tous les résultats intermédiaires ne peuvent avoir qu’une longueur au plus égale à 2 n chiffres. Selon l’analyse ci-dessus relative à l’addition, cela signifie que chaque addition distincte de produits intermédiaires nécessite au plus 2 n opérations de base. Pour nos n − 1 additions de ces nombres, nous avons donc besoin au plus de (n – 1) × (2 n) = 2 n2 − 2 n opérations de base.
En pratique, nous ne calculons pas ces additions intermédiaires, nous préférons additionner successivement tous les chiffres présents dans chaque colonne, en commençant par la colonne de droite, sans oublier de prendre en compte la retenue éventuelle. Mais cela revient au même pour le nombre global d’opérations élémentaires.
Conjointement avec les 2 n2 opérations de base pour calculer les produits intermédiaires, cela fait donc au total au plus 4 n2 − 2 n opérations de base, pour multiplier deux nombres de n chiffres avec la méthode scolaire ; dont n2 sont des multiplications élémentaires. Le nombre d’additions est ici évidemment surestimé, car les premières additions sont plus petites, mais l’ordre de grandeur est respecté (qu’il y ait en réalité environ n ou n2 additions).
Qu’est-ce que cela signifie concrètement ? Si nous voulons effectuer des calculs sur des nombres vraiment longs, disons avec 100 000 chiffres, nous avons alors besoin de presque 40 milliards d’opérations de base pour une seule multiplication, dont 10 milliards de multiplications élémentaires. Nous avons besoin d’environ 200 000 opérations arithmétiques en moyenne pour chaque chiffre de sortie distinct d’un tel produit. C’est un rapport manifestement très défavorable, et il devient d’autant plus défavorable que les nombres deviennent plus longs : avec 1 million de chiffres, nous avons besoin de presque 4000 milliards d’opérations de base (dont mille milliards de multiplications élémentaires), cela fait en moyenne environ 2 millions d’opérations de base pour un seul chiffre du résultat.
Considérons maintenant que la multiplication est une opération plus coûteuse que l’addition, ce qui est souvent le cas en pratique, et essayons d’améliorer le coût en temps de la multiplication.
2. L’algorithme de Karatsuba

Anatolii Alexeevich Karatsuba. Photo : Wikipédia.
Examinons à présent une méthode qui permet de multiplier deux nombres de n chiffres avec sensiblement moins d’opérations de base. Elle porte le nom du mathématicien russe Anatolii Alexeevich Karatsuba, qui a eu l’idée centrale de cette méthode (publiée en 1962 avec Yuri Ofman). Nous décrivons cette méthode tout d’abord pour les nombres comportant un, deux ou quatre chiffres, ensuite pour les nombres de longueur n quelconque.
Le cas le plus simple est la multiplication de deux nombres à un chiffre (n = 1) ; par exemple 8 × 4 = 32. Pour cela, on n’a besoin que d’une opération de base, à savoir une seule multiplication élémentaire qui fournit directement le résultat.
Le cas suivant que nous considérons est le cas n = 2, donc la multiplication de deux nombres a et b à deux chiffres. Écrivons-les à partir de leur décomposition en chiffres :
a = p × 10 + q et b = r × 10 + s.
Par exemple, pour a = 78 et b = 21, la décomposition en chiffres est la suivante :
p = 7 et q = 8 ; r = 2 et s = 1.
Voici comment se présente le produit a × b exprimé à partir de la décomposition en chiffres de ses deux facteurs :
a × b = (10 × p + q) × (10 × r + s)
= (p × r) × 100 + (p × s + q × r) × 10 + q × s.
Pour l’exemple ci-dessus (a = 78 et b = 21), on a
78 × 21 = (7 × 2) × 100 + (7 × 1 + 8 × 2) × 10 + 8 × 1 = 1638.
On voit ici directement qu’on peut calculer le produit des nombres a et b à deux chiffres en effectuant quatre multiplications de nombres à un chiffre et en additionnant les résultats (décalés les uns par rapport aux autres). C’est précisément ce que fait la méthode scolaire de la multiplication.
Nous devons à Karatsuba la découverte du fait que trois multiplications de nombres à un chiffre suffisent. Les valeurs à calculer sont les suivantes :
u = p × r,
v = (q − p) × (s − r),
w = q × s.
Mais pourquoi cela présente-t-il un intérêt pour la multiplication ? C’est parce que l’égalité suivante s’applique :
u + w − v = p × r + q × s − (q − p) × (s − r) = p × s + q × r
L’astuce de Karatsuba réside alors dans le fait qu’on peut exprimer le produit a × b à l’aide de cette équation, comme suit :
a × b = u × 102 + (u + w − v) × 10 + w.
Contrairement à la méthode scolaire, le calcul de v fait intervenir des soustractions. Nous avons donc besoin de définir la soustraction de deux nombres à un chiffre comme autre opération de base similaire à l’addition, que nous devons appliquer ici deux fois. Techniquement, les résultats (q − p) et (s − r) n’ont certes qu’un chiffre, mais peut-être un signe négatif. Quand on les multiplie, pour obtenir v, on doit tout d’abord effectuer une multiplication élémentaire de ces deux valeurs et ensuite déterminer le signe selon les règles habituelles (« moins par moins égale plus », etc.).
Calculons le produit a × b pour notre exemple a = 78 et b = 21. On a
u = 7 × 2 = 14
v = (8 − 7) × (1 – 2) = −1
w = 8 × 1 = 8
Ainsi, nous trouvons ce qui suit :
78 × 21 = 14 × 100 + (14 + 8 − (−1)) × 10 + 8
= 1400 + 230 + 8
= 1638.
Nous n’avons utilisé que trois multiplications élémentaires au lieu de quatre, auxquelles s’ajoutent plusieurs additions et soustractions pour le calcul des résultats intermédiaires.
La méthode de Karatsuba appliquée aux nombres à quatre chiffres
Après le cas n = 2, tournons-nous à présent vers le cas n = 4, c’est-à-dire la multiplication de deux nombres a et b à quatre chiffres. Exactement comme ci-dessus, nous pouvons les séparer chacun en deux moitiés p et q ou r et s ; mais ces moitiés de nombres ne sont à présent plus des nombres à un chiffre, mais des nombres à deux chiffres, de telle sorte que :
a = p × 10 2 + q et b = r × 10 2 + s.
À partir de ces quatre moitiés, nous calculons de nouveau les trois produits auxiliaires avec la méthode de Karatsuba, de la même façon que pour les nombres à deux chiffres :
u = p × r,
v = (q − p) × (s − r),
w = q × s
et comme précédemment, nous obtenons le produit de a et b à partir de ces trois produits auxiliaires :
a × b = u × 104 + (u + w − v) × 10 2 + w.
Exemple : Calculons a × b pour a = 5678 et b = 4321. Nous séparons d’abord a et b en moitiés p = 56 et q = 78 ainsi que r = 43 et s = 21. Ensuite, nous calculons les produits auxiliaires, à l’aide de la méthode de Karatsuba pour les nombres à deux chiffres :
u = 56 × 43 = 2408
v = (78 − 56) × (21 − 43) = −484
w = 78 × 21 = 1638
Il en résulte :
5678 × 4321 = 2408 × 10000 + (2408 + 1638 − (−484)) × 100 + 1638 = 24080000 + 453000 + 1638 = 24534638.
Pour ce calcul, nous avons dû former trois produits auxiliaires de nombres à deux chiffres, et nous venons justement de voir dans la partie précédente la façon de les obtenir par la méthode de Karatsuba. Pour chaque produit auxiliaire, on a besoin de trois multiplications élémentaires. Pour multiplier deux nombres à quatre chiffres selon la méthode de Karatsuba, nous avons donc besoin au total de 3 × 3 = 9 multiplications élémentaires, ainsi que de plusieurs additions et soustractions. Avec la méthode scolaire, nous aurions eu besoin de 16 multiplications élémentaires et de plusieurs additions.
La méthode de Karatsuba pour n’importe quels grands nombres
En continuant selon le même principe, nous pouvons ramener la multiplication de nombres à 8 chiffres à trois multiplications de nombres à 4 chiffres, la multiplication de nombres à 16 chiffres à trois multiplications de nombres à 8 chiffres, et ainsi de suite. En d’autres termes, pour la méthode de Karatsuba expliquée ci-dessus, la longueur n des deux nombres a et b peut être une quelconque puissance de 2, telle que 2 = 21, 4 = 2 × 2 = 22, 8 = 2 × 2 × 2 = 23, 16 = 2 × 2 × 2 × 2 = 24, etc.
Nous pouvons écrire la méthode de Karatsuba sous une forme générale de la façon suivante. Nous décomposons deux nombres a et b de longueur n = 2 × 2 × 2… × 2 = 2k sous la forme :
a = p × 10 n/2 + q et b = r × 10n/2 + s
et calculons ensuite leur produit avec trois multiplications de nombres de longueur n/2 = 2k−1 du type
a × b = p × r × 10n + (p × r + q × s − (q − p) × (s − r)) × 10 n/2 + q × s
Ainsi, le nombre de multiplications élémentaires nécessaires pour multiplier des nombres de longueur 2k n’est que le triple de celui nécessaire pour multiplier des nombres de longueur 2k−1 (au lieu du quadruple avec la méthode scolaire). Il en résulte donc le tableau suivant, qui récapitule le nombre de multiplications élémentaires nécessité respectivement par la méthode de Karatsuba et la méthode scolaire, pour multiplier des nombres d’une certaine longueur n :
| Longueur | Méthode de Karatsuba | Méthode scolaire |
|---|---|---|
| 1 = 20 | 1 | 1 |
| 2 = 21 | 3 | 4 |
| 4 = 22 | 9 | 16 |
| 8 = 23 | 27 | 64 |
| 16 = 24 | 81 | 256 |
| 32 = 25 | 243 | 1 024 |
| 64 = 26 | 729 | 4 096 |
| 128 = 27 | 2 187 | 16 384 |
| 256 = 28 | 6 561 | 65 536 |
| 512 = 29 | 19 638 | 262 144 |
| 1024 = 210 | 59 049 | 1 048 576 |
| … | … | … |
| 1 048 576 = 220 | 3 486 784 401 | 1 099 511 627 776 |
| … | … | … |
| n = 2k | 3k | 4k |
Nombre de multiplications nécessaires.
Celui qui maîtrise le calcul avec les logarithmes peut aussi facilement exprimer les entrées de ce tableau en fonction de n : dans la colonne relative à la méthode scolaire, on a la valeur 4k pour n = 2k. Nous écrivons log pour le logarithme de base 2. Ainsi, k = log(n) et
4k = 4log(n) = (2log(4))log(n) = nlog(4) = n2.
Par contre, avec la méthode de Karatsuba, on a
3k = 3log(n) = (2log(3))log(n) = nlog (3) = n1,58….
Comparons à présent le tableau à notre analyse de la méthode scolaire pour la multiplication de nombres d’un million de chiffres. La méthode scolaire nécessite presque quatre mille milliards d’opérations de base, dont mille milliards pour les multiplications élémentaires. Pour pouvoir appliquer la méthode de Karatsuba en lieu et place de la méthode scolaire, nous devons tout d’abord écrire encore une série de zéros devant un million de chiffres pour arriver à la puissance de deux immédiatement supérieure, à savoir 220 = 1 048 576. (Autrement, nous ne pourrions pas continuer à diviser la longueur par 2, jusqu’à ce que nous arrivions à 1.) Nous pouvons ensuite multiplier avec la méthode de Karatsuba et pour cela, nous n’avons besoin « que » d’environ trois milliards et demi de multiplications élémentaires (voir le tableau). Précisément, on n’a besoin que d’un 287-ième du temps de la méthode scolaire. (Par comparaison, une seconde comparée aux proverbiales « cinq minutes » représente un 300-ième.)
Nous voyons donc que la méthode de Karatsuba est considérablement plus économique en temps de calcul ; du moins lorsque – comme nous le faisons – on ne compte que les multiplications élémentaires. Pour une analyse vraiment précise, on devrait aussi considérer le temps engendré par l’addition et la soustraction des résultats intermédiaires. On préférerait alors peut-être calculer nos exemples concernant les nombres à deux et quatre chiffres selon la méthode scolaire. Mais dès que les nombres deviennent assez longs, c’est la méthode de Karatsuba qui gagne à tous les coups, parce qu’elle produit beaucoup moins de résultats intermédiaires que la méthode scolaire. La longueur exacte à partir de laquelle elle est plus rapide dépend des propriétés de l’ordinateur utilisé.
Pour faire une analyse fine de l’algorithme de Karatsuba, on devrait donc tenir compte à la fois des multiplications, des additions et des soustractions.
- Pour les multiplications, comme on l’a vu, cela dépend de la longueur du nombre. Plus précisément, pour multiplier des nombres de taille n, on a besoin de multiplier trois fois des nombres de taille n/2. Si l’on écrit cela sous une forme mathématique, et que l’on note K(n) le nombre de multiplications à effectuer pour l’algorithme de Karatsuba sur des nombres de taille n, on obtient que
K(n) = 3 K(n/2)
ce qui donne bien
K(n) = n log (3) = n 1,58… - On considère que les soustractions ont le même coût que les additions. Le coût est de n pour ajouter ou soustraire deux nombres de taille n. Pour l’algorithme de Karatsuba, récapitulons les additions nécessaires pour multiplier deux nombres de taille n :
- on calcule q – p et s – r où q, p, s et r sont de taille n/2, ce qui fait deux additions de taille n/2, c’est-à-dire un coût de n,
- on calcule ensuite p × r + q × s − (q − p) × (s − r) ce qui fait deux additions supplémentaires de taille n, soit 2 n,
- on ajoute ensuite les trois morceaux calculés précédemment (qui sont multipliés par les puissances de 10 adaptées), ce qui fait deux additions supplémentaires de taille n, soit 2 n.
À la fin, on a donc effectué deux additions de taille n/2 et quatre additions de taille n, soit un coût total de 5 n.
Si l’on souhaite donc calculer le coût total de l’algorithme de Karatsuba K'(n) avec les additions et les multiplications, on obtient que K'(n) = 3 K'(n/2) + 5 n dont la solution est que K'(n) ~ K(n) = n log (3).
Les additions sont bien négligeables dans cet algorithme, car leur coût est absorbé par celui des multiplications.
Résumons-nous pour conclure : quelle est la recette du succès de la méthode de Karatsuba ?
Elle découle de deux idées cruciales.
La première idée est tout-à-fait générale. La tâche à accomplir « multiplier deux nombres de longueur n » est ramenée à plusieurs tâches du même type, mais de moindre dimension, à savoir : « multiplier deux nombres de longueur n/2 ». Ainsi, nous réduisons le problème jusqu’à ce qu’il soit devenu assez simple (« multiplier deux nombres à un chiffre »). On appelle ce principe divide and conquer (diviser pour régner), et nous l’avons déjà vu en action dans d’autres algorithmes (par exemple, pour un tri plus rapide). Pour les différentes dimensions du problème, on ne programme naturellement pas à chaque fois une nouvelle procédure, mais on écrit une procédure pour la longueur générale n, qui s’auto-appelle à différentes reprises pour la dimension réduite du problème n/2. On appelle cela une récursion, et c’est effectivement une des techniques les plus importantes en informatique.
La seconde idée, spécifique à la multiplication, est l’astuce de Karatsuba, grâce à laquelle on n’a besoin de résoudre que trois sous-problèmes au lieu de quatre lors de chaque étape intermédiaire. Cette différence en apparence minuscule fournit une énorme économie sur toute la récursion et constitue l’avantage décisif de la méthode de Karatsuba par rapport à la méthode scolaire.
Les auteurs remercient H. Alt, M. Dietzfelbinger et C. Klost pour leurs remarques utiles.
Une première version de ce document est parue en allemand dans la série Algorithmus der Woche publiée à l’occasion de l’Année de l’informatique (Informatikjahr) 2006.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Arno Eigenwillig

Kurt Mehlhorn