
Programmation des échecs et d’autres jeux
Une première version de cet article a été initialement publiée sur Interstices en 2012 puis mise à jour en juin 2023.
Dans les années 90, les ordinateurs sont devenus capables de jouer contre de grands joueurs d’échecs et de les mettre en difficulté. En 1997, Garry Kasparov, champion du monde, est battu par Deep Blue. En 2005, le programme Hydra (sur un ordinateur parallèle puissant) écrase Michael Adams, un des meilleurs joueurs du monde, sur le score de 5 ½ à ½. Désormais, des programmes commerciaux généralistes sur des machines usuelles sont devenus aussi forts que les meilleurs joueurs humains. Ils gagneront contre vous presque à coup sûr, même en vous donnant des avantages divers (par exemple un pion d’avance).
Selon quels principes les programmes qui ont permis ces exploits sont-ils conçus ? Les techniques présentées ici peuvent servir à programmer de nombreux jeux, et sont proches de techniques utilisables pour résoudre d’autres problèmes.
Le graphe de pile ou face
Les échecs étant bien compliqués, regardons comment programmer un jeu beaucoup plus simple : pile ou face. Commençons même par un exemple encore plus simple : imaginons que nous ayons une pièce truquée qui tombe toujours sur pile. Nous savons alors que pour gagner, il faut choisir « pile », et que si l’on choisit « face », on va perdre. Le graphe représentant ce problème est le suivant :
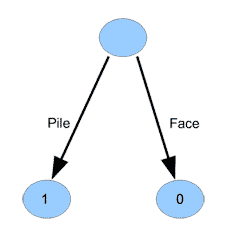
Nous avons donc représenté un jeu (certes très simple ici) par un graphe, c’est-à-dire des nœuds (les ronds) reliés par des arêtes (les flèches). Nous avons placé un \(1\) pour la situation finale conduisant à une victoire, et un \(0\) pour la situation finale conduisant à une défaite.
Généralisons à présent ce principe d’un graphe pour représenter un jeu, mais cette fois-ci avec deux joueurs : le premier choisit pile ou face, et le second, qui entend la décision du premier joueur, place la pièce selon son propre choix, sur pile ou sur face. Si le premier joueur a deviné ce qu’allait faire le second, il gagne ; sinon, le second joueur gagne. Ce jeu n’est pas beaucoup plus intéressant que le précédent, pourriez-vous objecter, car s’il joue bien, le second joueur peut toujours gagner ! Vous avez raison, mais ce qui est intéressant, c’est que cela peut être démontré grâce à la représentation par un graphe. Ce jeu se présente comme suit :
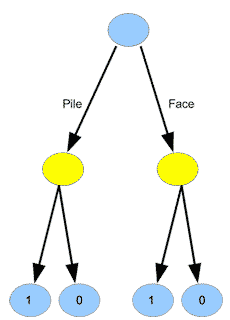
Il y a maintenant des nœuds bleus et des nœuds jaunes dans le graphe. Si on se place du point de vue du joueur 1, les nœuds jaunes correspondent aux situations où son adversaire prend une décision. En partant du haut de l’arbre, le joueur 1 choisit la branche descendante de son choix lorsque le nœud est bleu, et le joueur 2 choisit la branche de son choix lorsque le nœud est jaune. Là encore, les \(1\) marquent les victoires du joueur 1 et les \(0\) ses défaites.
Quoique le jeu ne soit pas bien compliqué, on n’a pas immédiatement accès à une stratégie pour le premier joueur. En regardant le nœud tout en haut, et même les nœuds juste en dessous, nous ne savons pas ce que le joueur 1 devrait jouer. Par contre, dans chacun des nœuds jaunes, nous voyons bien que le second joueur a une stratégie très simple pour gagner. Nous pouvons donc étiqueter les nœuds jaunes avec des \(0\) et des \(1\), tout comme les nœuds terminaux. Nous constatons que pour chacun de ces nœuds, le joueur 2 peut gagner (en choisissant face dans le cas où le joueur 1 a choisi pile, et en choisissant pile dans le cas où le joueur 1 a choisi face). Ces situations sont donc équivalentes à des défaites pour le joueur 1 ; par conséquent, nous les étiquetons \(0\). Nous obtenons alors le graphe suivant :
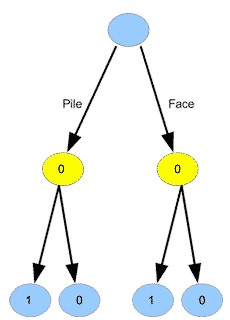
Nous constatons que quel que soit le choix du joueur 1, il se retrouve en situation \(0\) (perdante). On peut donc étiqueter aussi le nœud tout en haut d’un \(0\), montrant que la situation initiale est synonyme de défaite pour le joueur 1 :
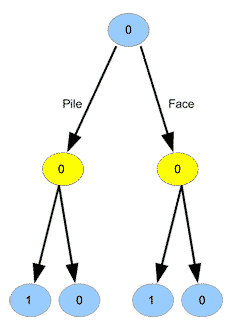
La procédure à appliquer est donc la suivante :
- écrire le graphe représentant le jeu
- étiqueter les nœuds avec des \(0\) et des \(1\) (éventuellement avec des ½ pour les cas d’égalité), en remontant depuis les nœuds du bas de l’arbre, jusqu’à la racine. Un nœud a pour valeur le maximum des nœuds fils, lorsque le nœud est bleu ; et le minimum des nœuds fils lorsque le nœud est jaune.
Nous obtenons ainsi deux certitudes :
- nous savons que si les joueurs jouent « bien », le joueur 2 gagne ;
- nous savons que le joueur 2 doit jouer une arête menant à un \(0\) pour gagner.
Bien sûr, nous avons examiné un jeu très simple, mais fondamentalement cette approche permet, théoriquement, d’étudier des jeux compliqués, dans la mesure où la mémoire de l’ordinateur et le temps de calcul permettent de réaliser toutes les opérations requises. Cette approche pour résoudre un jeu s’appelle le Minimax. Son inconvénient est le très long temps de calcul qu’il nécessite, dès lors que le jeu s’approche d’un jeu réel.
Le cas du jeu d’échecs
Le nombre inscrit dans nos nœuds (0, 1 ou ½ dans les exemples ci-dessus) est appelé valeur du nœud (on parle aussi de la valeur de la situation). Pour résoudre un jeu avec l’outil présenté ci-dessus, il faut écrire une valeur dans chaque nœud. C’est faisable sur les jeux triviaux ci-dessus, ou sur des jeux comme tic-tac-toe, mais pas pour le jeu d’échecs, où une telle approche demanderait un temps déraisonnable.
Pour traiter le jeu d’échecs, Claude Shannon a proposé en 1950 une approximation de cet algorithme. Pour définir cette approximation, nous allons avoir besoin d’une définition : on définit la profondeur d’un nœud comme le nombre d’arêtes à parcourir avant de remonter à la racine. On décide alors d’une profondeur limite \(k\). Pour tous les nœuds à profondeur \(k\) ou les nœuds où le jeu est fini, la valeur sera :
- un nombre positif très élevé (par exemple 100 000) en cas de victoire dans cette situation ;
- un nombre très négatif (par exemple -100 000) en cas de défaite dans cette situation ;
- une valeur approchée, calculée à partir des éléments visibles sur le plateau, par exemple pour les échecs, comme suit :
- 10 pour une dame (-10 pour la dame adverse) ;
- 5 pour une tour (-5 pour une tour adverse) ;
- 3 pour un cavalier ou un fou (-3 pour un cavalier ou fou adverse) ;
- 1 pour un pion (-1 pour un pion adverse) ;
en prenant en compte aussi des éléments de position, comme -½ pour chaque pion « doublé » (deux pions sur la même colonne).
Une telle approximation est appelée « fonction d’évaluation ». Il se trouve que des fonctions assez simples fournissent de très bons résultats, et qu’on arrive efficacement à améliorer ces fonctions en discutant avec des experts.
- Solution 1 : par expertise humaine.
Dans cette solution, de loin la plus usuelle, on utilise un maximum d’expertise humaine, et de validations par essais et erreurs. On prend en compte un maximum d’effets, la valeur des pièces, leur mobilité (nombre de coups légal), la protection assurée au roi, les menaces, et autres…
On développe en fait, pour plus de précision, plusieurs fonctions d’évaluation : une pour le début de partie, une pour la suite de partie, une lorsqu’on se rapproche de la fin (la toute fin de partie étant du domaine des tables de Nalimov).
Les fonctions d’évaluation ne sont habituellement pas publiques — on peut trouver de bonnes fonctions d’évaluation publiques, mais les programmes les plus forts gardent en général cette partie critique confidentielle. - Solution 2 : par apprentissage automatique.
Cette solution est très difficile à mettre en œuvre. Elle permet de faire l’économie d’un travail fastidieux de synthèse manuelle d’une fonction d’évaluation, mais ne permet pas d’atteindre le meilleur niveau. La seule exception est pour les tables de Nalimov (qu’on peut voir comme une fonction d’évaluation parfaite dédiée aux fins de partie), construites grâce à une forte automatisation (quoiqu’en utilisant aussi une partie d’expertise humaine pour accélérer le processus).
Procédons ensuite comme à la section précédente : calculons les valeurs dans les nœuds du graphe par récurrence, mais nous n’avons plus besoin de descendre plus bas que la profondeur \(k\) pour pouvoir calculer les valeurs des nœuds :
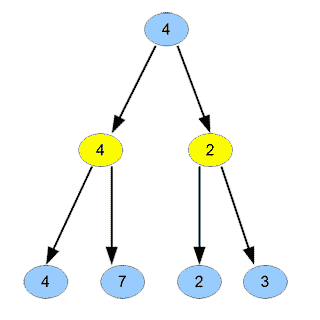
Nous pouvons alors jouer le coup qui conduit à un nœud de valeur maximale. Mais étudions plus en détails la figure ci-dessus. En général, un programme parcourt le graphe ci-dessus de gauche à droite, descendant dans les nœuds les plus profonds d’abord. Le \(4\) jaune est le minimum entre \(4\) et \(7\). Le \(2\) jaune est ensuite le minimum entre \(2\) et \(3\). Mais en fait, lors du calcul du \(2\) jaune, dès que nous voyons le \(2\) bleu, nous savons que la valeur obtenue sera \(2\) ou moins que \(2\). Or, un nœud frère a valeur \(4\) ; nous en déduisons donc que de toute façon le nœud \(2\) jaune sera inutile, car le joueur 1 préférera de toutes façons aller vers le nœud étiqueté \(4\). Il n’est donc pas utile de descendre au nœud étiqueté \(3\). Graphiquement, cela se traduit sur le graphe qui suit par le fait que, quelle que soit la valeur du nœud bleu « \(?\) », le nombre en haut du graphe sera \(4\).
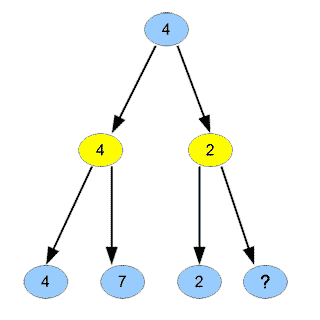
Inutile donc d’étudier ce nœud bleu « \(?\) ». Ici, le bénéfice apparaît petit (il suffit de visiter 6 nœuds au lieu de 7), mais si, au lieu de ce nœud, nous avions un immense graphe, le bénéfice serait conséquent.
On parle d’élagage. Ce principe se généralise : lorsque l’on sait que la valeur obtenue sera plus petite qu’un certain nombre beta, quelles que soient les valeurs futures dans une branche du graphe, et qu’en même temps on sait qu’on n’obtiendra jamais plus qu’un certain alpha dans une sous-branche (et beta est supérieur ou égal à alpha), alors on peut « couper » cette branche et se passer de l’étudier. Ce principe est appelé « élagage alpha-beta ». La figure qui suit (inspirée de Wikipedia) montre le déroulement d’un algorithme minimax avec élagage alpha-beta :
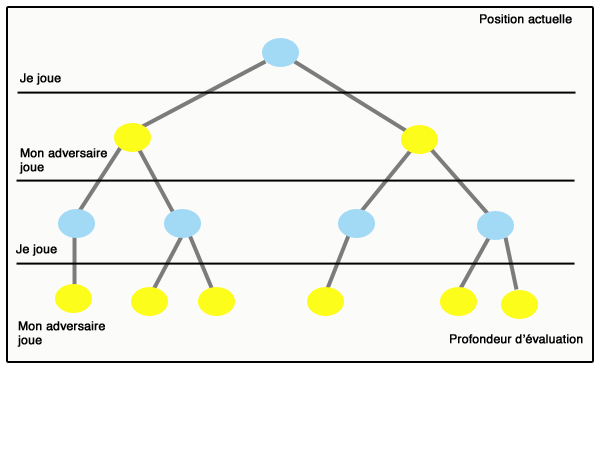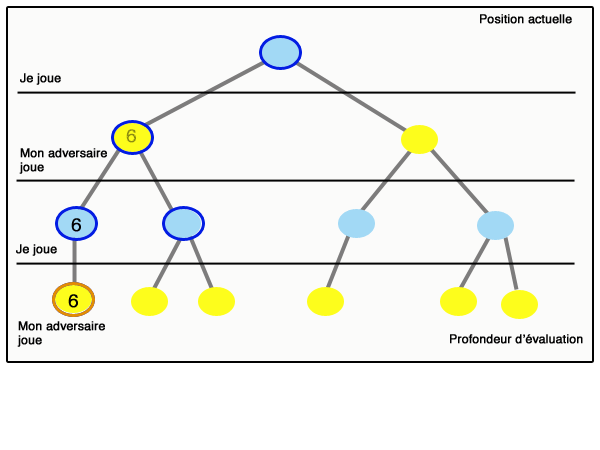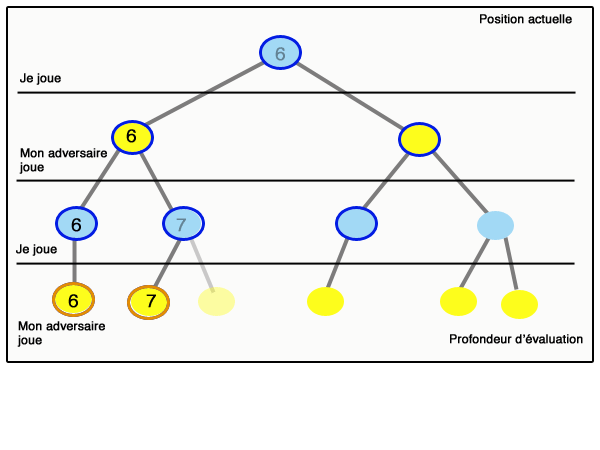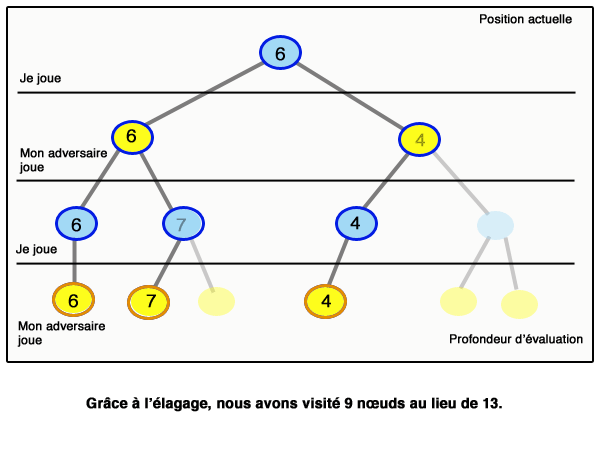
Il est important de bien comprendre que l’élagage alpha-beta est d’autant plus efficace que l’on aura placé les bons nœuds à gauche. Un article scientifique de Donald Knuth et Ronald Moore, paru en 1975 et célèbre parmi les informaticiens, montre que si l’ordre des nœuds est aléatoire, alors le nombre de nœuds parcourus pour aller à la profondeur d lorsque l’on a b actions possibles par situation est de l’ordre de b3d/4 ; tandis qu’on obtient un résultat de l’ordre de bd sans alpha-beta, et de l’ordre de bd/2 = √bd si on commence toujours par les meilleures actions (cas évidemment très optimiste).
Que manque-t-il maintenant ?
L’approche ci-dessus est très opérationnelle sur de nombreux jeux, mais diverses améliorations permettent d’augmenter encore grandement les performances :
- Approfondissement itératif : on travaille tout d’abord à profondeur k=1, puis k=2, puis k=3, et ainsi de suite ; la valeur obtenue pour k=2 est utilisée pour trier les actions possibles lors de l’approfondissement à k=3, d’où un élagage alpha-beta plus efficace.
- Construction de bibliothèques d’ouvertures, permettant de calculer un grand nombre de coups de très grande qualité pour le début de partie.
- Calcul exact des fins de partie, par ce que l’on appelle les tables de Nalimov. On connaît exactement la valeur d’une situation dès lors que le nombre de pièces atteint 6 ou moins, ainsi qu’un grand nombre de cas avec 7 pièces. Cela signifie que l’ordinateur joue à la perfection, et très rapidement, dès que l’on arrive dans ces cas. La construction minimax ou alpha-beta est aussi beaucoup plus rapide dès lors qu’un grand nombre de branches atteignent le niveau des tables de Nalimov.
- Parallélisation : pour une performance optimale, plusieurs processeurs sont utilisés (quelques dizaines en général, 64 pour les célèbres matchs Hydra contre Adams), chacun descendant dans des branches différentes de l’arbre. Cette parallélisation est loin d’être triviale à réaliser.
- Tables de transposition : plusieurs branches peuvent atteindre la même situation, il convient donc de stocker les valeurs calculées via une table de hachage pour économiser en temps de calcul.
À quels jeux s’attaquer avec ces principes ?
Une première limitation est que nous avons supposé que le jeu est à information parfaite : on connaît exactement tout l’état du jeu. Mais ce n’est de loin pas le cas de tous les jeux. Les jeux à information imparfaite sont par exemple le Poker, le Bridge, le Scrabble. Lorsque l’information cachée est critique (par exemple pour le Poker, le Bridge, et aussi les « échecs sombres » qui sont une variante partiellement observable des échecs), les algorithmes deviennent souvent très heuristiques. Cela signifie qu’ils contiennent de nombreuses astuces spécifiques au jeu, et ne sont pas mathématiquement prouvés efficaces (ce qui certes ne les empêche pas d’être performants).
Une seconde limitation est que nous avons supposé qu’il n’y avait aucun hasard. Cette limitation est usuellement aisée à lever : il suffit d’introduire un troisième type de nœuds : à côté des nœuds où moi, joueur 1, je décide l’action, et des nœuds où mon adversaire, joueur 2, décide l’action, introduisons des nœuds où l’action est tirée au sort. Le nombre à inscrire dans ces nœuds est la moyenne (pondérée adéquatement) des nombres inscrits dans les nœuds où le hasard peut mener. L’algorithme n’est donc pas à modifier de fond en comble.
Une troisième limitation est que nous avons supposé que l’on pouvait commodément fournir une valeur approchée pour un nœud – en utilisant une fonction d’évaluation. C’est une forte limitation en fait : de nombreux jeux où les ordinateurs sont longtemps restés faibles, face à l’humain, sont des jeux où l’on ne sait pas fournir une valeur approchée de la valeur d’une situation. Par exemple, le fameux jeu de Go, un des grands défis des chercheurs et chercheuses dans le domaine des jeux, est un cas où estimer la valeur d’une situation est très difficile. Les années 2006-2010 ont vu l’essor de nouvelles techniques permettant de traiter ces jeux bien mieux que par le passé — le Monte Carlo Tree Search (MCTS), dit aussi Fouille d’arbre Monte-Carlo en français et né à Lille. Les humains sont restés de loin supérieurs aux machines pendant toute cette période, jusqu’à ce que le MCTS soit combiné avec les réseaux de neurones comme dans Alpha-Zero et, plus généralement, l’apprentissage Zéro.
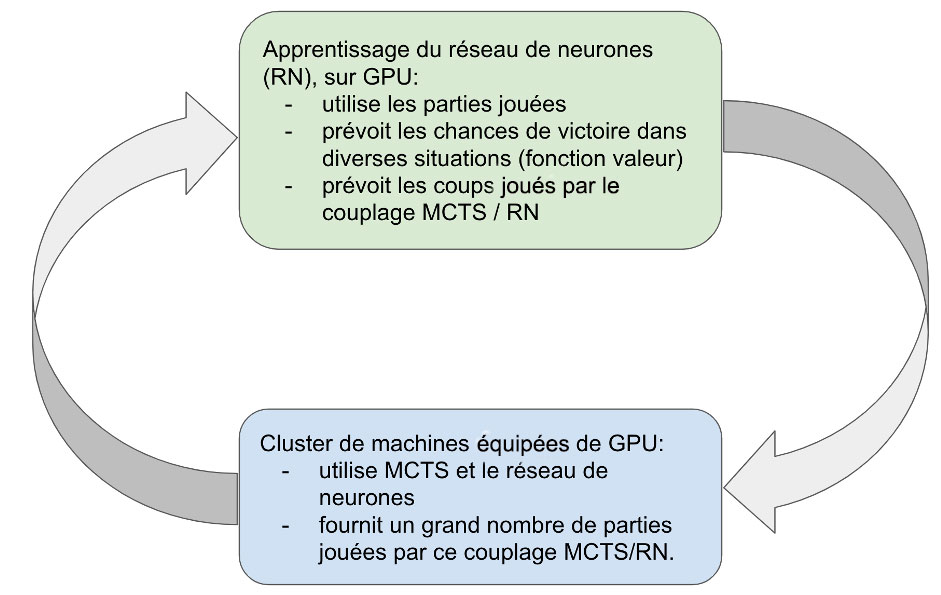
Schéma simplifié de l’apprentissage Zéro.
La fouille d’arbres Monte-Carlo est basée sur des travaux de type Monte Carlo pur, consistant à évaluer une position en simulant aléatoirement un grand nombre de parties depuis cette position. Attention néanmoins à ne pas sous-estimer la complexité de ces algorithmes, qui va au-delà de ce principe simple : en effet, les simulations sont aléatoires, mais avec une subtile façon, modifiée dynamiquement, de gérer les tirages au sort.
À quoi bon tout ça ?
Les jeux sont certes un plaisir, et ils ont une portée pédagogique. Mais peut-être vous demandez-vous si le jeu en vaut vraiment la chandelle ? N’y a-t-il pas des activités plus utiles ? Revenons tout d’abord sur l’utilisation en pratique de ces approches. Il convient de souligner que le principe minimax est exactement similaire à la programmation dynamique utilisée abondamment dans l’industrie ; et que l’élagage alpha-beta est un exemple parmi d’autres d’élagages très utiles en parcours d’arbre et en programmation par contraintes. Enfin, les méthodes présentées s’appliquent aussi pour la planification adversariale, lorsque l’on cherche à optimiser des choix futurs au pire cas sur diverses incertitudes.
Enfin, et surtout, les jeux fournissent un fascinant défi pour l’intelligence artificielle. Il est critique de comprendre ce que nous savons programmer, ou non, des activités humaines. Les jeux sont un outil parfait pour tester nos outils d’intelligence artificielle dans un cadre où la compétition avec nos collègues du monde entier est claire et nette. C’est pour ce rôle qu’à côté d’applications plus industrielles, nous nous intéressons aux jeux, notamment des jeux plus difficiles pour les ordinateurs que les échecs. Revenons sur quelques-unes des pistes en cours d’exploration.
Les directions de recherche
On a vu récemment une révolution avec l’arrivée de réseaux de neurones combinés à la fouille d’arbre Monte Carlo, le tout utilisant des puissances de calcul formidables basées sur l’utilisation de GPU. Ceci a en particulier permis de battre les joueurs humains au Go, avec notamment la victoire d’AlphaGo sur le champion Lee Sedol, deuxième au niveau mondial, en 2016. Depuis 2012, date de parution de la première version de cet article, il convient de mentionner plusieurs autres avancées récentes.
- Les réseaux de neurones sont aussi utilisés à l’intérieur de l’élagage alpha-beta présenté au début de cet article, pour obtenir une meilleure fonction valeur. Un inconvénient, toutefois, est le temps de calcul associé aux réseaux de neurones. En 2018, un article révolutionnaire a proposé la technique “NNUE” (en anglais), qui permet de calculer la sortie d’un réseau de neurones beaucoup plus vite lorsque les nombreux cas d’applications sont proches les uns des autres. Cette méthode est centrale par exemple dans le programme d’échecs StockFish, qui gagne de nombreuses compétitions mondiales d’échecs et notamment les meilleurs codes de Zero learning (voir l’article en anglais « Stockfish 8 versus AlphaZero »).
- Le Zero learning a été largement amélioré, notamment en France, de manière à apprendre d’abord sur un petit plateau de jeu (pour maîtriser la tactique) puis sur un grand plateau (pour affiner la stratégie), afin de rendre tractables des plateaux beaucoup plus grands. Ainsi, pour la première fois, en 2020 l’ordinateur a battu l’humain aux jeux de Havannah et de Hex, même en grande taille (voir l’article en anglais « Polygames: Improved Zero Learning »).
- Cependant les attaques adversariales, après avoir été appliquées en vision par ordinateur — notamment en montrant que l’on peut tromper beaucoup de méthodes de reconnaissance neuronale, se sont avérées pertinentes aussi en jeux. Alors que les humains semblaient irrémédiablement battus par les ordinateurs au jeu de Go, en 2022 des chercheurs ont réussi à construire une méthode capable de battre KataGo, considéré jusque là comme super-humain au jeu de Go. (Une méthode est dite super-humaine quand elle est capable d’explorer une plus grande profondeur de coups qu’un humain). Mieux : la méthode employée est utilisable par un joueur amateur humain, qui peut ainsi battre KataGo par lui-même.
- À grands renforts d’ingénierie par d’importantes équipes, les jeux de stratégie en temps réel tels que Starcraft, ou de collaboration tels que Diplomacy en 2022, ont été dominés par l’ordinateur.
Remerciements à mes confrères de jeux : Bruno Bouzy, Tristan Cazenave, Sylvain Gelly, Jean-Baptiste Hoock, Arpad Rimmel, Abdallah Saffidine, Fabien Teytaud, Dennis Soemers, Vegard Mella, Jeremy Rapin, Xavier Martinet, Vasil Khalidov, Yves Costel, ainsi qu’à l’équipe d’Interstices.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

