
Comment fonctionne une machine de Turing ?
Car c’est bien une machine abstraite qu’Alan Turing a inventée pour expliquer la notion de « procédure mécanique » : on parle d’algorithme. Cette machine est la plus élémentaire possible destinée à mettre en œuvre ces mécanismes de calcul, numériques ou symboliques, comme le font notamment les ordinateurs. Ne perdons pas de vue que lorsqu’Alan Turing décrit sa machine dans un article en 1936, les ordinateurs n’existent pas encore !
Essayons de la découvrir… en l’utilisant
La machine imaginée par Turing comporte un ruban divisé en cases, dans lesquelles elle peut écrire des symboles. La machine ne peut lire qu’une seule case à la fois, de même elle écrit dans une seule case et décale le ruban d’une seule case vers la gauche ou vers la droite. Les symboles sont en nombre fini. Pour que sa machine fonctionne comme une machine à calculer en binaire, Turing envisage le cas particulier où les symboles utilisés sont 0 et 1. C’est une telle machine que nous vous proposons de tester sur l’animation interactive suivante. Vous pourrez y suivre l’exécution de six « programmes ».
Animation HTML5/JS réalisée par Hugo Lehmann, Centrale Lille Projets, librement adaptée d’une applet Java écrite par Hamdi Ben Abdallah.
L’entrée du programme est une liste de symboles binaires, écrits sur le ruban, matérialisé par les cases successives (en bas de l’animation). Une fois le calcul effectué, c’est sur ce ruban que sera écrit le résultat du calcul, la sortie du programme. À chaque instant, le ruban mémorise l’état du calcul. Voilà la forme la plus simple de mémoire mécanique !
À chaque programme correspond une description sous forme de table (à droite de l’animation). Chacune des lignes de cette table est associée à un état et spécifie les actions à effectuer quand la machine est dans cet état, en fonction du symbole présent sous la tête de lecture. Ces actions peuvent être l’écriture d’un symbole (ici un 0 ou un 1) et le déplacement du ruban d’une case à droite ou à gauche. La ligne spécifie également le nouvel état après l’exécution des actions.
La machine s’arrête quand un état marqué comme final est atteint.
Turing a également prévu que les programmes, tels qu’ils sont décrits par la table, puissent eux aussi être codés en binaire et inscrits sur un deuxième ruban. Chaque code correspond alors à une instruction possible. Le calcul se déroule automatiquement en passant d’une instruction à une autre. Comme il est possible d’inscrire sur ce deuxième ruban toutes sortes de programmes et de les exécuter, ce mécanisme va pouvoir faire (avec beaucoup de patience !) tout ce qu’un ordinateur peut faire. On parle de machine de Turing universelle.
Six « programmes » au choix
À vous ! Choisissez d’abord un « programme » parmi les six que nous vous proposons ici. Vous trouverez ci-dessous une description détaillée de chacun d’eux.
Pour ajouter 1 à un nombre binaire, on utilise la table d’addition suivante :
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 : on pose 0, et on retient 1
Si le nombre binaire en entrée se termine par 0, par exemple :
1001010 + 1 = 1001011
dans ce cas, il suffit de remplacer le dernier 0 par un 1. On parcourt le nombre de gauche à droite, et lorsqu’on arrive à la fin, si on trouve un 0, on le remplace par un 1 et on passe à l’état final.
Si le nombre binaire en entrée se termine par 1, par exemple :
1001011 + 1 = 1001100
dans ce cas, après avoir parcouru le nombre de gauche à droite, on revient de droite à gauche, tant qu’on trouve un 1, on le remplace par un 0, lorsqu’on trouve la première occurrence de 0, on la remplace par 1 puis on passe à l’état final.
Cas particulier de nombre se terminant par 1, un nombre peut être formé seulement par des 1, par exemple :
1111111 + 1 = 10000000
dans ce cas, on remplace tous les 1 par 0 et on insère un 1 dans la première case vide à gauche.
Passons maintenant à la programmation de notre machine.
La table d’actions utilisée est la suivante :
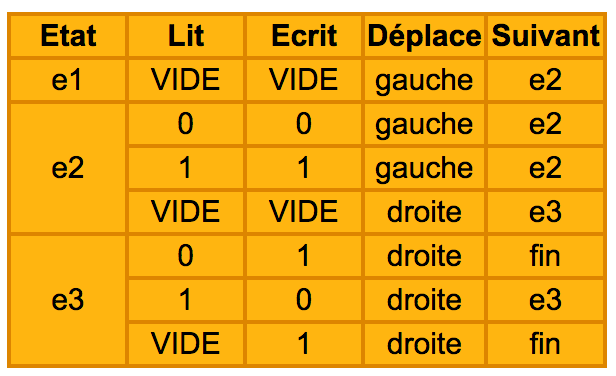
Voici comment se comporte la machine :
Si elle est à l’état 1 et trouve une case vide, elle n’écrit rien, décale le ruban d’une case à gauche et passe à l’état 2.
Si elle est à l’état 2 et lit un 0, elle écrit 0, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et lit un 1, elle écrit 1, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et trouve une case vide, elle n’écrit rien, décale le ruban à droite et passe à l’état 3.
Si elle est à l’état 3 et lit un 1, elle écrit 0, décale le ruban à droite et reste à l’état 3.
Si elle est à l’état 3 et lit un 0, elle écrit 1, décale le ruban à droite et passe à l’état final.
Si elle est à l’état 3 et trouve une case vide, elle écrit 1, décale le ruban à droite et passe à l’état final.
Pour soustraire 1 à un nombre binaire, on utilise la table de soustraction suivante :
0 – 0 = 0
0 – 1 = 1 : on pose 1, et on retient 1
1 – 0 = 1
1 – 1 = 0
Si le nombre binaire en entrée se termine par 1, par exemple :
1001011 – 1 = 1001010
dans ce cas, il suffit de remplacer le dernier 1 par un 0. On parcourt le nombre de gauche à droite, et lorsqu’on arrive à la fin, si on trouve un 1, on le remplace par un 0 et on passe à l’état final.
Si le nombre binaire en entrée se termine par 0, par exemple :
1001010 – 1 = 1001001
dans ce cas, après avoir parcouru le nombre de gauche à droite, on revient de droite à gauche, tant qu’on trouve un 0, on le remplace par un 1, lorsqu’on trouve la première occurrence de 1, on la remplace par 0 puis on passe à l’état final.
Passons maintenant à la programmation de notre machine.
La table d’actions utilisée est la suivante :
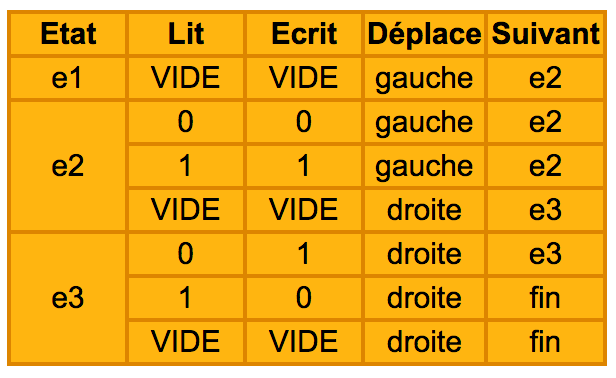
Voici comment se comporte la machine :
Si elle est à l’état 1 et trouve une case vide, elle n’écrit rien, décale le ruban d’une case à gauche et passe à l’état 2.
Si elle est à l’état 2 et lit un 0, elle écrit 0, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et lit un 1, elle écrit 1, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et trouve une case vide, elle n’écrit rien, décale le ruban à droite et passe à l’état 3.
Si elle est à l’état 3 et lit un 0, elle écrit 1, décale le ruban à droite et reste à l’état 3.
Si elle est à l’état 3 et lit un 1, elle écrit 0, décale le ruban à droite et passe à l’état final.
Pour la multiplication des nombres binaires, on utilise la table suivante :
1 × 0 = 0
1 × 1 = 1
0 × 0 = 0
En binaire, 2 est noté 10. Cette multiplication revient donc, comme la multiplication par 10 en notation décimale, à ajouter au nombre de départ un 0 à droite, par exemple :
1001010 × 10 = 10010100
on parcourt donc le nombre de gauche à droite, et dès qu’on trouve une case vide à droite, on y insère un 0 et on passe à l’état final.
Passons maintenant à la programmation de notre machine.
La table d’actions utilisée est la suivante :
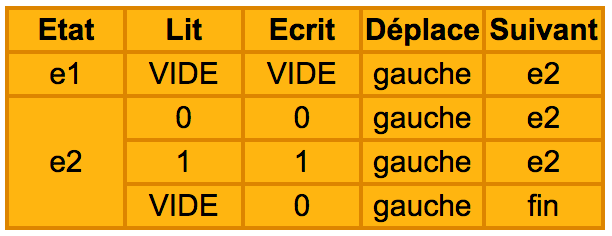
Voici comment se comporte la machine :
Si elle est à l’état 1 et trouve une case vide, elle n’écrit rien, décale le ruban d’une case à gauche et passe à l’état 2.
Si elle est à l’état 2 et lit un 0, elle écrit 0, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et lit un 1, elle écrit 1, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et trouve une case vide, elle écrit 0, décale le ruban à gauche et passe à l’état final.
Il s’agit d’inverser les 0 et les 1 formant un nombre binaire (les 1 deviennent des 0 et les 0 des 1) et de recommencer indéfiniment.
On commence par parcourir le nombre de gauche à droite en remplaçant les 1 par des 0 et les 0 par des 1, puis lorsqu’on rencontre une case vide, on parcourt le nombre dans l’autre sens en remplaçant à nouveau les 0 par des 1 et les 1 par des 0.
Passons maintenant à la programmation de notre machine.
La table d’actions utilisée est la suivante :
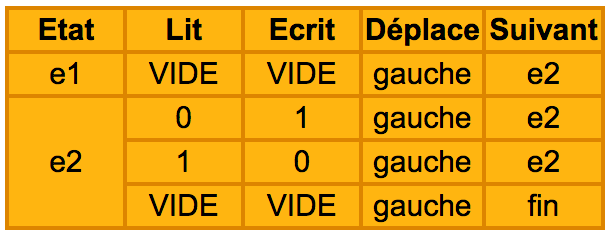
Voici comment se comporte la machine :
Si elle est à l’état 1 et trouve une case vide, elle n’écrit rien, décale le ruban d’une case à gauche et passe à l’état 2.
Si elle est à l’état 2 et lit un 0, elle écrit 1, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et lit un 1, elle écrit 0, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et trouve une case vide, elle n’écrit rien, décale le ruban à droite et passe à l’état 3.
Si elle est à l’état 3 et lit un 1, elle écrit 0, décale le ruban à droite et reste à l’état 3.
Si elle est à l’état 3 et lit un 0, elle écrit 1, décale le ruban à droite et passe à l’état 3.
Si elle est à l’état 3 et trouve une case vide, elle n’écrit rien, décale le ruban à gauche et passe à l’état 2.
Il s’agit précisément de doubler la longueur d’une suite de 1 inscrits sur le ruban. Pour cela, on parcourt le ruban de gauche à droite, à chaque 1 rencontré, on le remplace par un 0, on retourne vers la gauche et dans la première case vide on ajoute un 0, puis on repart de gauche à droite. Lorsqu’on atteint la première case vide à droite, on parcourt à nouveau le ruban en sens inverse et on remplace tous les 0 par des 1.
Passons maintenant à la programmation de notre machine.
La table d’actions utilisée est la suivante :
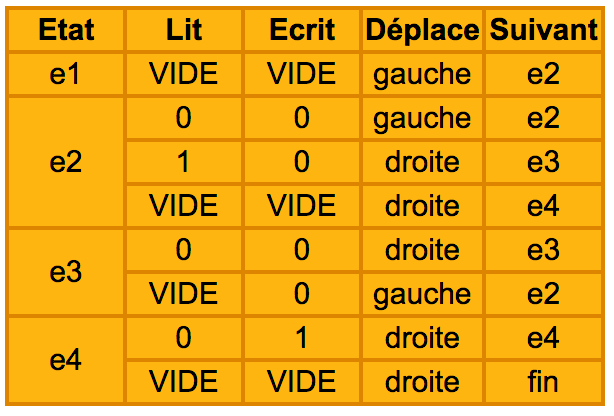
Voici comment se comporte la machine :
Si elle est à l’état 1 et trouve une case vide, elle n’écrit rien, décale le ruban d’une case à gauche et passe à l’état 2.
Si elle est à l’état 2 et lit un 0, elle écrit 0, décale le ruban à gauche et reste à l’état 2.
Si elle est à l’état 2 et lit un 1, elle écrit 0, décale le ruban à droite et passe à l’état 3.
Si elle est à l’état 2 et trouve une case vide, elle n’écrit rien, décale le ruban à droite et passe à l’état 4.
Si elle est à l’état 3 et lit un 0, elle écrit 0, décale le ruban à droite et reste à l’état 3.
Si elle est à l’état 3 et trouve une case vide, elle écrit 0, décale le ruban à gauche et passe à l’état 2.
Si elle est à l’état 4 et lit un 0, elle écrit 1, décale le ruban à droite et reste à l’état 4.
Si elle est à l’état 4 et trouve une case vide, elle n’écrit rien, décale le ruban à droite et passe à l’état final.
Un palindrome est un mot qui est identique qu’on le lise de gauche à droite ou de droite à gauche. Par exemple, 101 est un palindrome alors que 100 n’en est pas un.
Le principe d’une Machine de Turing qui teste si un mot binaire écrit sur son ruban est un palindrome est d’itérer les étapes suivantes tant qu’on n’atteint pas l’état OUI ou l’état NON :
on lit le premier symbole de la partie codante du ruban et on l’efface en mémorisant sa valeur (0 ou 1) par un état (e3 ou e6 dans la table d’actions ci-dessous)
on déplace le ruban sans changer d’état jusqu’à atteindre la première case vide.
On passe alors dans l’état e4 (respectivement e7) si on était dans l’état e3 (respectivement e6)
et on recule d’une case pour se positionner sur le dernier symbole de la partie codante du ruban.
si ce symbole est 1 (respectivement 0) alors qu’on est dans l’état e4 mémorisant que le premier symbole était un 0 (respectivement l’état e7 mémorisant que le premier symbole était un 1), on passe dans l’état NON ;
sinon on efface ce dernier symbole et si la partie codante est vide, on passe dans l’état OUI, sinon on déplace le ruban jusqu’à se positionner au début de la partie codante.
La table d’actions utilisée est la suivante :
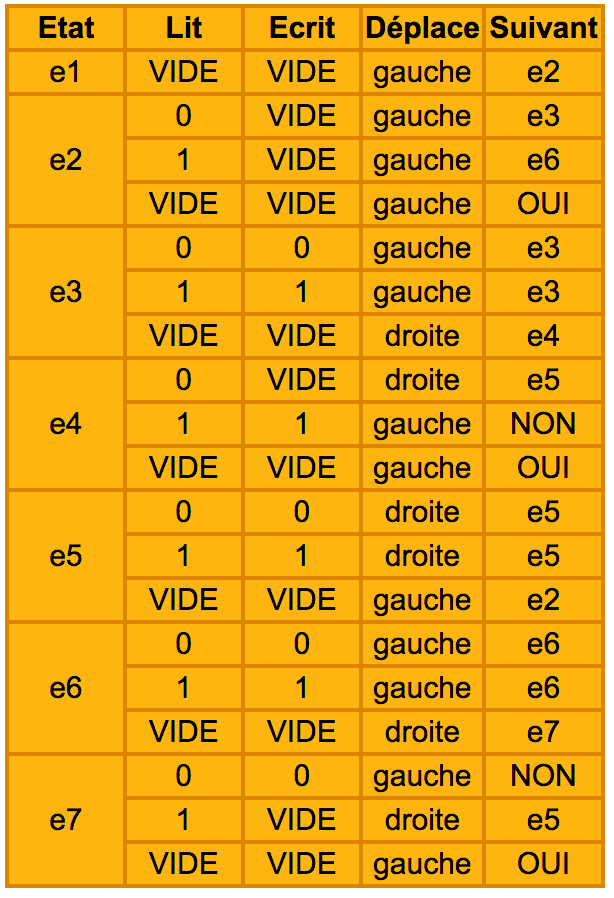
Voici comment se comporte la machine :
Si elle est à l’état 1 et trouve une case vide, elle n’écrit rien, décale le ruban d’une case à gauche et passe à l’état 2.
Si elle est à l’état 2 et lit un 0, elle efface la case, décale le ruban à gauche et passe à l’état 3.
Si elle est à l’état 2 et lit un 1, elle efface la case, décale le ruban à gauche et passe à l’état 6.
Si elle est à l’état 2 et trouve une case vide, elle n’écrit rien, décale le ruban à gauche et passe à l’état final OUI.
Si elle est à l’état 3 et lit un 0, elle écrit 0, décale le ruban à gauche et reste à l’état 3.
Si elle est à l’état 3 et lit un 1, elle écrit 1, décale le ruban à gauche et reste à l’état 3.
Si elle est à l’état 3 et trouve une case vide, elle n’écrit rien, décale le ruban à droite et passe à l’état 4.
Si elle est à l’état 4 et lit un 0, elle efface la case, décale le ruban à droite et passe à l’état 5.
Si elle est à l’état 4 et lit un 1, elle écrit 1, décale le ruban à gauche et passe à l’état final NON.
Si elle est à l’état 4 et trouve une case vide, elle n’écrit rien, décale le ruban à gauche et passe à l’état final OUI.
Si elle est à l’état 5 et lit un 0, elle écrit 0, décale le ruban à droite et reste à l’état 5.
Si elle est à l’état 5 et lit un 1, elle écrit 1, décale le ruban à droite et reste à l’état 5.
Si elle est à l’état 5 et trouve une case vide, elle n’écrit rien, décale le ruban à gauche et passe à l’état 2.
Si elle est à l’état 6 et lit un 0, elle écrit 0, décale le ruban à gauche et reste à l’état 6.
Si elle est à l’état 6 et lit un 1, elle écrit 1, décale le ruban à gauche et reste à l’état 6.
Si elle est à l’état 6 et trouve une case vide, elle n’écrit rien, décale le ruban à droite et passe à l’état 7.
Si elle est à l’état 7 et lit un 0, elle écrit 0, décale le ruban à gauche et passe à l’état final NON.
Si elle est à l’état 7 et lit un 1, elle efface la case, décale le ruban à droite et passe à l’état 5.
Si elle est à l’état 7 et trouve une case vide, elle n’écrit rien, décale le ruban à gauche et passe à l’état final OUI.
Entrez un nombre binaire, puis en utilisant les touches « Commencer » ou « Pas-à-Pas », regardez s’exécuter le programme.
Ces programmes sont rudimentaires mais très instructifs : ils montrent que l’on peut faire des opérations numériques (les 0 et les 1 correspondent au codage binaire de nombres) ou symboliques (les 0 ou les 1 codent des symboles).
Ouf ! Pas facile de suivre à la fois le calcul pas à pas et de se représenter en même temps globalement ce qui est calculé ! Nous voilà, en quelque sorte, à l’échelle « atomique » du calcul, devant les briques de base de ce qui compose tous les algorithmes.
En effet, en combinant ces briques de base, ce sont tous les algorithmes qui peuvent s’implémenter. Par exemple, en ajoutant plusieurs fois 1, nous pouvons additionner plusieurs nombres, puis en combinant les additions faire des multiplications, et de proche en proche tous les calculs numériques, tandis que des procédés similaires s’appliquent aux calculs symboliques.
De fait, nous pourrions très bien reproduire aussi ces calculs avec un ruban de papier, un crayon et une gomme. Car peu importe le support utilisé : les mécanismes algorithmiques s’incarnent dans un grand nombre de dispositifs physiques, qui peuvent ainsi être considérés comme équivalents.
Enfin, n’oublions pas non plus que c’est nous qui, en lisant le résultat d’un calcul, lui donnons un sens…
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
