Idée reçue : Si un problème est NP-complet, pas la peine de s’y attaquer
Avant d’expliquer pourquoi une affirmation aussi catégorique est en partie fausse, revenons sur la définition des problèmes P, NP et des problèmes NP-complets. En effet, les problèmes mathématiques sont classés selon leur complexité — une notion bien précise qui n’est pas synonyme de difficulté.
Un problème — par exemple « un entier n étant donné, s’agit-il d’un nombre composé et non d’un nombre premier ? » — est dit NP (pour Non déterministe Polynomial) si, en utilisant un algorithme qui fait des tirages au hasard, on peut espérer le résoudre en temps polynomial, c’est-à-dire avec une méthode dont le nombre d’étapes élémentaires de calcul est majoré par un polynôme dépendant de n (le paramètre du problème).
Pour les nombres composés, c’est le cas : en effet, avec de la chance, si n est composé et qu’en essayant au hasard vous faites la division de n par a, un de ses diviseurs (différents de 1 et de n), vous saurez immédiatement qu’il est composé (faire une division ne prend pas beaucoup de temps).
S’il existe un algorithme déterministe (ne faisant pas de tirage au hasard) permettant de déterminer la réponse à la question qui vous intéresse, le problème est dit polynomial, autrement dit, dans la classe P.
Il semble évident qu’il est plus facile de réussir en s’appuyant sur une chance parfaite qu’en ne comptant que sur la perspicacité des méthodes qu’on met en œuvre dans les algorithmes qu’on invente. C’est ce que tout le monde pense et cela signifie que :
P ≠ NP,
ou encore : il existe des problèmes que saura résoudre en temps polynomial un individu doté d’une chance exceptionnelle (comme celle de Gontran, le personnage de Walt Disney cousin de Donald), mais qu’un individu normal ne s’autorisant que des algorithmes déterministes ne saura pas résoudre en temps polynomial.
Aussi étonnant que cela puisse paraître, aujourd’hui on ne sait pas démontrer que P ≠ NP (voir P = NP, un problème à un million de dollars ?).
On sait cependant qu’il existe une catégorie de problèmes NP qui concentrent en eux toute la difficulté des problèmes NP. On les appelle NP-complets : savoir résoudre un seul problème NP-complet en temps polynomial déterministe, permettrait de résoudre tous les problèmes NP en temps polynomial déterministe. Inversement d’ailleurs, si on réussissait à démontrer qu’un problème NP-complet ne peut pas être résolu en temps polynomial déterministe, cela signifierait qu’aucun problème NP-complet ne peut l’être.
Puisqu’un problème NP-complet concentre en lui toute la difficulté de la classe NP, on est tenté de croire que nécessairement il est difficile, et donc que :
Si un problème est NP-complet, alors ce n’est pas la peine de s’y attaquer.
C’est ce qu’on entend souvent, et il semble que ce soit là une idée reçue très largement partagée, au point que certains considèrent même que dès qu’on a pu démontrer qu’un problème est NP-complet, alors, le travail est fini, on peut cesser de s’y intéresser sérieusement et d’y perdre son temps.
Nous allons voir que les choses sont plus compliquées que cela et qu’un point de vue plus juste et mesuré serait plutôt le suivant :
Si un problème est démontré NP-complet, alors, il est très vraisemblable qu’aucune méthode ne traitera efficacement toutes les instances du problème en temps raisonnable dans la pratique. Cependant, il se peut tout-à-fait qu’en moyenne, le problème soit assez facile et même parfois très facile, ou encore, que toutes les instances naturelles, qu’on rencontre vraiment dans le monde réel, soient faciles. Il ne faut donc pas renoncer à s’y intéresser mais au contraire étudier si, bien que du type NP-complet, il ne serait pas quand même abordable, et comment.
Voici deux cas qui vous prouveront qu’il faut être prudent et ne pas surinterpréter la propriété d’être NP-complet : la 3-coloriabilité et la satisfiabilité.
La 3-coloriabilité
Le problème de la 3-coloriabilité est le suivant :
Un graphe G est-il coloriable avec trois couleurs sans que deux nœuds reliés portent la même couleur ?
Il s’agit bien là d’un problème NP-complet.
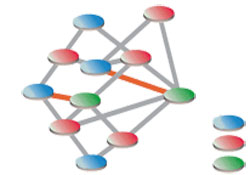
Exemple de graphe 3-coloriable.
Pourtant, si on considère que chaque graphe possible ayant le même nombre de nœuds a la même probabilité de se présenter (c’est là un point de vue tout à fait naturel), alors en utilisant un algorithme de recherche systématique simple — procédant par « backtracking » —, on montre qu’en moyenne pour un graphe de n nœuds, il faut 197 étapes de calcul pour savoir s’il est 3-coloriable ou non.
Le fait d’avoir fait une hypothèse sur la probabilité des divers graphes donne un sens précis à la notion de « temps moyen de résolution », d’où la possibilité de démontrer un tel résultat (qui est dû à Herbert S. Wilf, voir bibliographie).
Attention, le résultat n’indique pas «197n étapes, pour un graphe de n nœuds», mais bien :
197 étapes en moyenne, quel que soit le nombre n de nœuds du graphe.
La raison en est que dès que quatre nœuds sont reliés deux à deux, on peut conclure que le graphe n’est pas 3-coloriable et que cela se produit très fréquemment quand on considère des graphes au hasard, en envisageant que tous les graphes de n nœuds ont la même probabilité d’être proposés à l’algorithme.
Le problème de la 3-coloriabilité est difficile dans les mauvais cas — quand on réussit presque à le colorier avec trois couleurs et que ça ne marche pas au dernier moment — c’est ce qu’indique la propriété NP-complet.
Pourtant, en moyenne, il est très facile : les cas difficiles sont même extrêmement rares.
La satisfiabilité
Le problème le plus souvent cité comme problème NP-complet est le problème de la satisfiabilité d’un ensemble de clauses (par exemple : est-il possible de rendre simultanément vrai : [a ou b ou c], [a ou non b ou non c], [non a ou non b ou non c], [non b ou c] ?).
Sans être dans une situation aussi extrême que celle mentionnée pour la 3-coloriabilité, il s’agit cependant d’un problème NP-complet relativement facile. Bien souvent, soit on découvre rapidement que l’instance à traiter est satisfiable ; soit on voit rapidement qu’elle ne l’est pas, et les pires cas (ceux qui font que le problème est NP-complet) sont en définitive peu fréquents.
Ce problème fait l’objet de nombreuses recherches et les algorithmes pour le traiter progressent. Aucun ne sera bon dans tous les cas, mais le nombre de cas qui résistent se réduit et on réussit à traiter des instances de plus en plus grandes du problème. Là encore, le fait d’être NP-complet ne constitue pas un diagnostic définitif et ne doit pas être interprété comme une consigne pour cesser de s’attaquer au problème.
En résumé
Être NP-complet est un indice montrant qu’on pourrait avoir affaire à un problème difficile, et donc impossible à traiter en pratique dès que le paramètre du problème devient grand. Mais il se peut que les pires cas soient rares et donc le fait d’être NP-complet n’est pas un élément ultime de jugement.
Il faut savoir insister et analyser la fréquence des mauvais cas, et même se poser la question de leur présence dans les cas concrets que l’on aura à résoudre. Et c’est parfois bien autre chose !
Notons, pour terminer, qu’il existe une autre idée reçue du même type dont il faut se méfier. Croire que « si un problème est dans P (polynomial) alors c’est un problème facile en pratique » est assez souvent vrai. Cependant, si un problème est P, que le polynôme qui mesure la difficulté des plus mauvais cas est de degré 200 et que ces mauvais cas sont très fréquents, alors ce ne sera pas un problème facile du tout en pratique !
- Yuri Gurevich. The Challenger-Solver game: Variation on the theme P=?NP. Voir le PDF (172 Ko).
- Yuri Gurevich. Feasible Functions, 1994. Voir le PDF (44 Ko).
Sur la satisfiabilité :
- Boolean satisfiabilily problem sur Wikipedia (consulté le 25 novembre 2009)
- Herbert S. Wilf. Some Examples of Combinatorial Averaging. American Math. Monthly 92, 1985, pp.250-261
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).