Idée reçue : L’irrégularité, un vilain défaut
Presque tous nos sens sont d’accord là-dessus : ce qui est lisse est plus reposant pour l’œil. Nous imaginons les formes d’onde de la musique comme un déroulement régulier, alors que le bruit ne serait qu’une succession heurtée de sons. En faisant glisser notre main sur une forme, nous préférons la caresse des courbes douces aux agressions d’une courbe irrégulière et, pour nos papilles, l’onctuosité renvoie encore à une notion de texture unie. Une autre raison à notre préférence pour la régularité est que celle-ci est plus facilement appréhendée par notre cerveau, alors que son absence est souvent synonyme de complications : si une courbe lisse représente l’évolution d’un phénomène jusqu’à un instant donné, nous pensons pouvoir prévoir son futur proche juste en prolongeant la courbe de manière « naturelle ». Cette possibilité n’existe pas pour une courbe très irrégulière comme un cours de bourse.
L’irrégularité a un rôle essentiel…
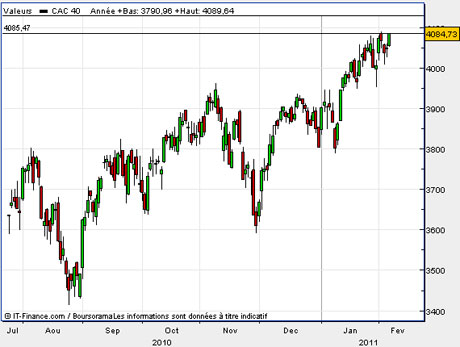
Cours du CAC 40 © Boursorama.
Pourtant, l’irrégularité joue un rôle essentiel dans le bon fonctionnement de nombreux phénomènes, aussi bien naturels qu’artificiels. Intuitivement, tout le monde sent bien ce que recouvre ce concept. Une courbe lisse typique est le graphe d’un polynôme, comme la fonction x → x2 que l’on étudie au lycée. Au contraire, l’évolution quotidienne du CAC 40, que l’on voit tous les jours s’afficher sur nos écrans lors des journaux télévisés, est foncièrement irrégulière. Il en est de même de l’électrocardiogramme que notre médecin décrypte pour connaître l’état de santé de notre cœur. Mais y a-t-il une seule manière d’être irrégulier, ou au contraire, l’irrégularité présente-t-elle plusieurs visages ? Un peu d’observation et de réflexion montre qu’il y a au moins deux dimensions bien distinctes, que nous appellerons rugosité et discontinuité.
La rugosité, c’est par exemple l’état de la surface d’une feuille de papier que l’on aurait chiffonnée et roulée en boule avant de la déplier de nouveau. La surface n’est plus lisse, pour autant, si on a pris soin de ne pas déchirer le papier, elle reste continue. La surface des pierres, une échographie ou l’électrocardiogramme d’une personne en bonne santé sont d’autres instances de phénomènes rugueux. En revanche, chez une personne souffrant d’un trouble cardiaque comme l’arythmie, on peut voir apparaître sur l’électrocardiogramme des discontinuités, c’est-à-dire des sauts, en plus de l’aspect rugueux. Des discontinuités sont aussi présentes en permanence sur les courbes décrivant le trafic sur Internet.
Le cas des cours financiers est particulièrement intéressant, car il combine très souvent ces deux types d’irrégularités : l’évolution des prix des entreprises du CAC 40 est presque en permanence rugueuse. Et des événements comme les annonces stratégiques d’une société, un indicateur économique loin du consensus ou un bouleversement géopolitique introduisent, plus souvent qu’on ne le croit, des discontinuités dans les cotations. Ces deux types d’irrégularités entraînent deux types de risques qu’il faut traiter par des méthodes différentes. Bien d’autres exemples naturels ou artificiels combinent ces deux irrégularités : la surface des montagnes par exemple, qui est presque partout rugueuse, est ponctuée par endroits de discontinuités comme les failles. Pour ces deux types d’irrégularités, il est important de comprendre que la situation est dynamique : la rugosité, ainsi que la fréquence et la hauteur des sauts, évoluent au cours du temps, et ces évolutions sont souvent riches d’enseignement sur le phénomène.
En sus des deux dimensions que nous venons de décrire, les mathématiciens ont identifié de nombreuses autres « couleurs » de l’irrégularité, comme disent les Anglo-Saxons. Elles sont cependant moins intuitives, et dépassent le cadre de cet article. Comme le montrent les exemples ci-dessus, l’irrégularité est omniprésente, aussi bien dans la nature que dans les réalisations humaines. On peut s’interroger sur les raisons d’une telle ubiquité.
… et sa présence est indispensable
En réalité, dans beaucoup de cas, l’irrégularité est non seulement présente, mais elle est aussi indispensable : le fonctionnement même du phénomène dépend d’une certaine dose de rugosité et/ou de sauts.
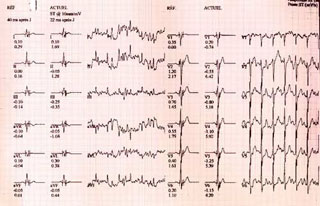
Électrocardiogramme d’un test d’effort. Source : Flickr © Eric Delcroix.
Un cas particulièrement représentatif est celui des électrocardiogrammes. Le fonctionnement du cœur, et en particulier la fréquence cardiaque, est régulé par l’interaction permanente et complexe entre deux systèmes : le système parasympathique, responsable du ralentissement de cette fréquence, et le système orthosympathique, qui agit en sens contraire. Ce mode de contrôle est la cause de l’aspect irrégulier des électrocardiogrammes. On peut ainsi relier de façon quantitative l’état de santé du cœur à cette irrégularité : pour mesurer la rugosité d’une courbe, les mathématiciens ont mis au point des outils appelés « dimensions fractales ». Une courbe totalement lisse a une dimension 1, et plus elle est rugueuse, plus sa dimension se rapproche de 2, ce qui constitue le cas limite d’une courbe tellement irrégulière qu’elle passe par tous les points d’une région. De nombreuses études ont montré qu’un électrocardiogramme sain avait une dimension fractale de l’ordre de 1.7, ce qui est très élevé. Plus remarquable encore, la dégradation de l’état de santé d’un cœur donné, par exemple à la suite d’un infarctus, entraîne une diminution de cette dimension, et donc un accroissement de la régularité. En poussant les choses à l’extrême, un électrocardiogramme plat, correspondant à une personne décédée, est totalement lisse et a une dimension 1.
Plusieurs conclusions sont à tirer de cet exemple : premièrement, l’irrégularité est constitutive du phénomène, on ne peut la retirer sans supprimer le phénomène lui-même. Deuxièmement, une forte irrégularité n’est pas nécessairement néfaste, elle peut au contraire être un signe de bonne santé. Enfin, et c’est le plus important dans les applications, on peut mesurer la rugosité et s’en servir à des fins de diagnostic.
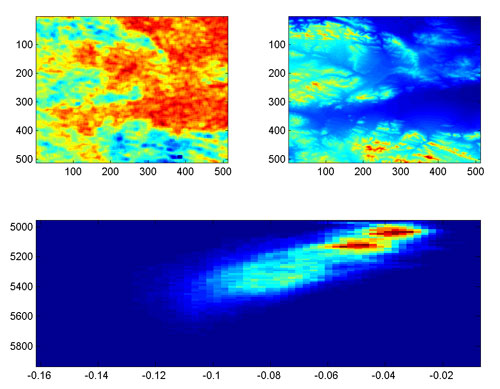
En haut à gauche : altitudes dans une région autour de l’Himalaya. Les zones de basse altitude sont en bleu, les plus hautes en rouge. En haut à droite : images des rugosités. Les zones les plus rugueuses sont en bleu, les moins rugueuses en rouge. En bas : relation entre altitude et régularité. On voit que les points de haute altitude sont les plus rugueux.
De nombreux autres phénomènes présentent des caractéristiques analogues. On peut relier la rugosité à l’altitude dans les montagnes et la forme de cette relation est un indicateur de l’âge du massif. La rugosité des cours boursiers est une conséquence directe de ce que les financiers appellent « l’efficience des marchés ». L’irrégularité du trafic sur Internet est la conséquence du protocole de transmission, appelé TCP, et sa mesure permet de comprendre divers comportements statistiques du réseau.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
