
Modéliser et simuler la fonte des calottes polaires
Cet article est à l’origine du module « Simuler la fonte des calottes polaires » primé lors de la compétition internationale des Mathématiques de la planète Terre.
La contribution des calottes polaires à la montée du niveau des mers est essentiellement la combinaison de trois phénomènes :
- la modification en surface des précipitations neigeuses et de la fonte de glace, à cause du changement climatique et du changement d’altitude du glacier ;
- l’amincissement des plateformes flottantes, qui fondent par en-dessous à cause du réchauffement de l’océan ;
- la décharge de glace dans l’océan, lorsque la glace s’écoule vers la mer puis se brise en larguant des icebergs.
Animation réalisée par Victoria Denys. Voir l’animation en pleine fenêtre.
Les épisodes de vêlage d’icebergs peuvent être particulièrement spectaculaires, comme le montre cette vidéo (en anglais) sur le glacier Jakobshavn au Groenland.
Le modèle mathématique
Tous ces processus physiques sont étudiés par des glaciologues, en collaboration avec des climatologues, océanographes, mathématiciens et informaticiens. Un modèle numérique, basé sur un modèle mathématique, permet de simuler l’évolution des calottes polaires, notamment le vêlage d’icebergs. Pour construire le modèle mathématique, on considère la calotte polaire comme un volume délimité par des frontières. Le modèle mathématique est un système d’équations qui traduit ce qui se passe à l’intérieur du glacier et à ses frontières. La surface est une frontière particulière qui bouge au cours du temps et dont l’évolution est traduite par une équation.
Animation réalisée par Victoria Denys. Voir l’animation en pleine fenêtre.
Le modèle numérique et la simulation
Il n’est pas possible de résoudre les équations du modèle mathématique, avec une formule pour calculer la vitesse et l’altitude de surface en chaque point de la calotte polaire et à chaque instant. Il faut avoir recours à un modèle numérique, qui modifie les équations et qui les résout sur ordinateur grâce à des algorithmes. On obtient ainsi une solution numérique approchée, avec une erreur que l’on sait contrôler mathématiquement.
La discrétisation en espace
La première étape est de passer des inconnues définies partout à des inconnues définies par un nombre fini de valeurs. Cette étape s’appelle une discrétisation spatiale. Pour cela, la surface du glacier est découpée en petits triangles, et l’épaisseur du glacier en tranches, ce qui aboutit à un découpage du volume glaciaire en prismes, qu’on appelle des mailles.
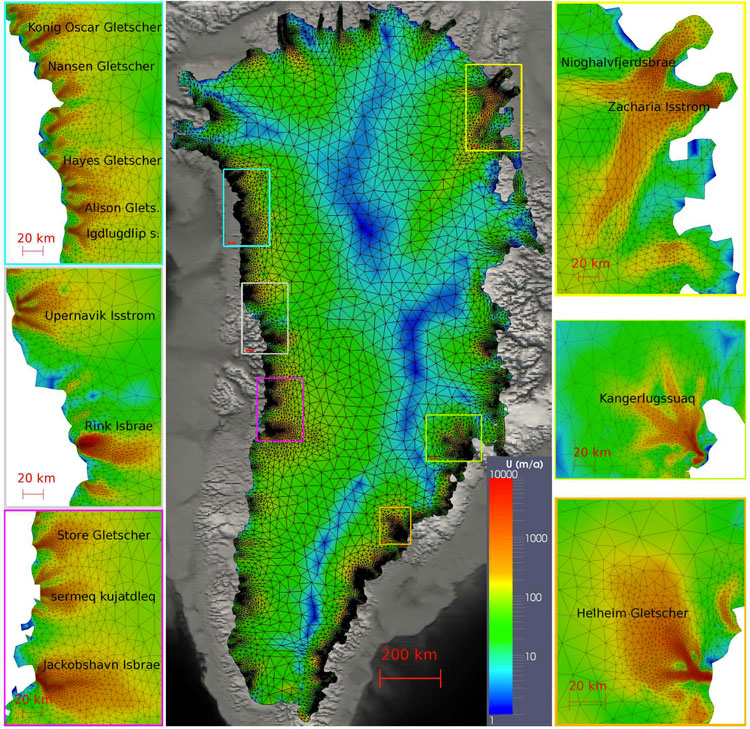
Maillage du Groenland et vitesse simulée. Il y a plus de triangles dans les zones des glaciers émissaires pour calculer précisément les variations rapides de la vitesse. Image d’après Gillet-Chaulet, F., Gagliardini, O., Seddik, H., Nodet, M., Durand, G., Ritz, C., Zwinger, T., Greve, R., and Vaughan, D. G.: Greenland ice sheet contribution to sea-level rise from a new-generation ice-sheet model, The Cryosphere, 6, 1561-1576, 2012. Licence CC-BY 3.0.
Pour calculer la vitesse et la pression à l’intérieur de la calotte polaire, connaissant l’altitude de surface, il faut résoudre les équations de Stokes discrétisées. Les équations aux dérivées partielles sont transformées en un système d’équations algébriques compliquées, avec autant d’équations que d’inconnues.
La discrétisation en temps
Pour déterminer l’altitude de surface, il faut en plus discrétiser le temps et calculer l’altitude à des instants réguliers, par exemple tous les ans. Pour cela, il faut actualiser le Bilan de Masse de Surface (BMS), qui dépend de la vitesse et des conditions météorologiques.
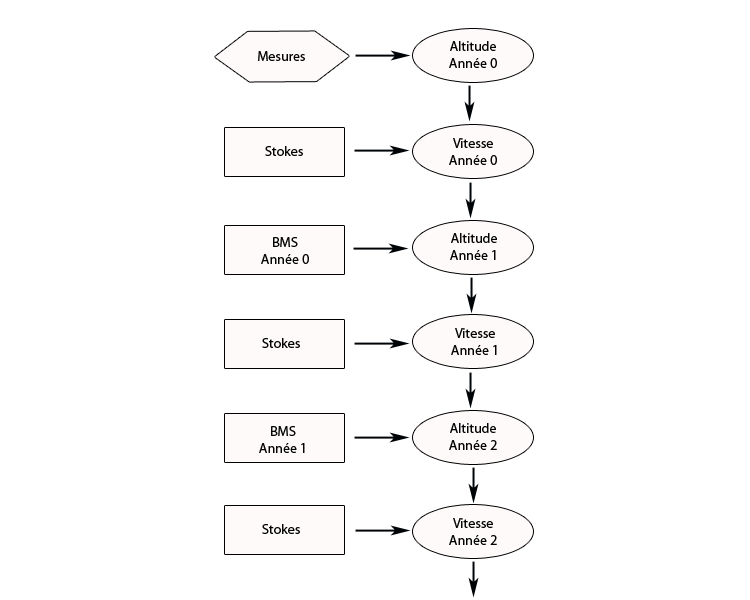
Connaissant grâce à des mesures l’altitude de surface pour l’année 0, on calcule la vitesse pour l’année 0, en résolvant les équations de Stokes discrétisées.
On calcule le Bilan de Masse de Surface pour l’année 0 et on en déduit l’altitude de surface pour l’année 1.
On calcule alors la vitesse pour l’année 1, puis le Bilan de Masse de Surface, puis l’altitude de surface pour l’année 2, etc.
La résolution des équations
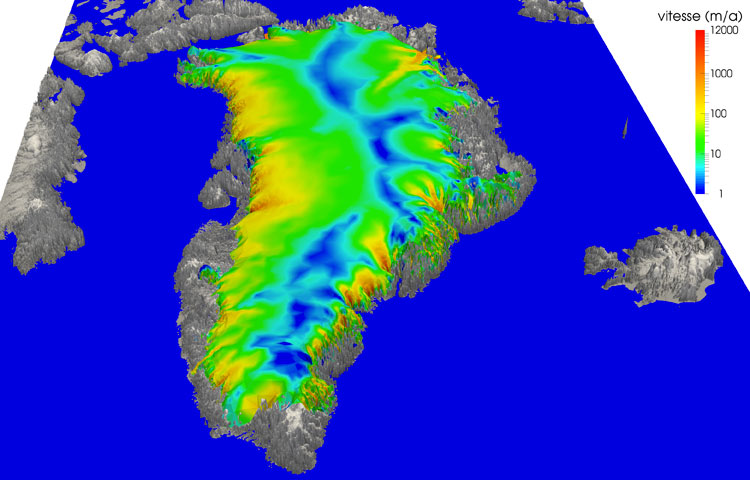
Vitesse simulée en 3D de la calotte polaire du Groenland. Les glaciers émissaires vont nettement plus vite (en rouge, 12 km par an) que les autres parties (en bleu, 1 m par an). Image : Fabien Gillet-Chaulet, CNRS & LGGE, Grenoble.
Pour résoudre les équations de Stokes discrétisées, il y a deux difficultés : d’une part, les équations sont non linéaires, avec des expressions mathématiques plus compliquées que de simples proportions ; d’autre part, le système contient beaucoup d’équations, environ quatre fois le nombre de mailles. On ne sait pas résoudre de façon exacte un tel système, alors on utilise un algorithme itératif, qui procède par approximations successives. On contrôle mathématiquement l’erreur et on arrête l’algorithme lorsque l’erreur est assez petite. Le nombre d’opérations de l’algorithme, et par conséquent le temps de calcul, augmentent avec le nombre d’équations, donc avec le nombre de mailles.
Mais pour avoir une bonne précision, il faut beaucoup de mailles, surtout dans les zones de forte vitesse. Comme dans la plupart des simulations numériques, il faut trouver un compromis entre la précision du résultat et le nombre d’opérations.
Le code informatique
Le modèle numérique est prêt, enfin presque. Il faut écrire un logiciel, dans un langage de programmation choisi, pour indiquer à l’ordinateur comment faire les calculs définis dans les schémas et les algorithmes. Le logiciel enchaîne plusieurs opérations, de la lecture des données à l’écriture des résultats, en passant par le maillage de l’inlandsis et les étapes de simulation.
Les scénarios de simulation
Le code informatique permet de simuler l’évolution de l’inlandsis, en appliquant divers scénarios. Ainsi, les modèles climatiques comme ceux du GIEC fournissent des données de précipitation et température de surface différentes selon le scénario socio-économique utilisé. Quant au coefficient de friction à la base, il peut rester stable ou varier au cours du temps.
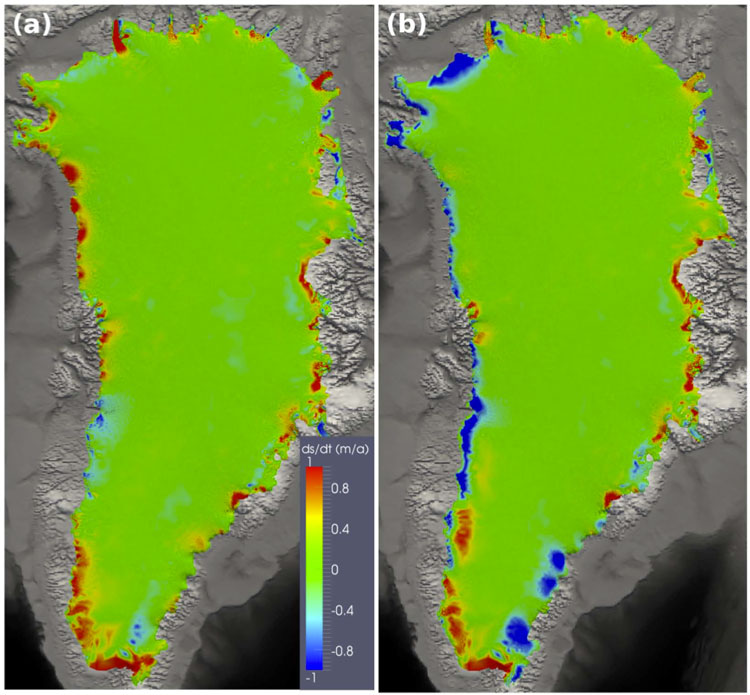
Simulation de l’évolution de l’altitude de surface en 10 ans : en rouge, l’altitude augmente, en bleu, elle diminue, en vert, elle ne bouge pas. Image d’après Gillet-Chaulet, F., Gagliardini, O., Seddik, H., Nodet, M., Durand, G., Ritz, C., Zwinger, T., Greve, R., and Vaughan, D. G.: Greenland ice sheet contribution to sea-level rise from a new-generation ice-sheet model, The Cryosphere, 6, 1561-1576, 2012. Licence CC-BY 3.0.
La figure ci-dessus montre des résultats de simulation pour une période de 10 ans, obtenus avec le modèle Elmer/Ice. Les conditions à la base restent identiques pour deux scénarios climatiques différents : (a) les conditions climatiques actuelles restent constantes pendant 10 ans (précisons que ceci n’est pas réaliste en raison du réchauffement actuel) ; (b) le scénario climatique est prédit par la moyenne de 18 modèles utilisant le scénario médian d’émissions de CO2 (scénario A1B du GIEC, voir le rapport de synthèse pour plus de détails). Les bords du Groenland s’épaississent pour le scénario (a) et s’amincissent pour le scénario (b), même en seulement 10 ans. On peut imaginer qu’en réalité, les conditions à la base deviendront plus favorables au glissement dans le futur, ce qui devrait produire un amincissement du Groenland plus fort et donc une perte de glace sous forme d’icebergs encore plus marquée.
Conclusion
Le modèle décrit ici a été utilisé pour simuler l’évolution du Groenland pendant un siècle. Il est également bien adapté pour simuler l’évolution des glaciers terrestres. Par exemple, le laboratoire de Glaciologie de Grenoble (LGGE) a récemment utilisé ce modèle pour évaluer un risque environnemental associé au glacier de Tête Rousse à Saint Gervais. À ce sujet, on pourra consulter aussi la vidéo « Le futur des glaciers » réalisée par Guillaume Jouvet.
Même avec l’aide de supercalculateurs, ces calculs prennent encore trop de temps.
Les glaciologues et les mathématiciens ne renoncent pas pour autant à la modélisation de l’Antarctique, ou du Groenland au-delà d’un siècle. En utilisant le fait que l’épaisseur de glace est très faible par rapport à l’étendue horizontale de la calotte, ils ont proposé un modèle simplifié, dit « modèle couche mince », un petit peu moins précis que le précédent, mais beaucoup plus rapide !
- Maëlle Nodet. De la glace à la mer. Matapli, SMAI, 2013.
- Guillaume Jouvet. L’évolution des glaciers, modélisation et prédiction. Accromath, Vol 8.2, 2013.
- Fabien Gillet-Chaulet. Elmer/Ice, un modèle de calotte polaire de nouvelle génération. Journée Mésochallenge Equip@meso, 2013.
- Catherine Ritz, Tamsin L. Edwards, Gaël Durand, Antony J. Payne, Vincent Peyaud & Richard C. A. Hindmarsh: Potential sea-level rise from Antarctic ice-sheet instability constrained by observations, Nature, 2015.
- Gillet-Chaulet, F., Gagliardini, O., Seddik, H., Nodet, M., Durand, G., Ritz, C., Zwinger, T., Greve, R., and Vaughan, D. G.: Greenland ice sheet contribution to sea-level rise from a new-generation ice-sheet model, The Cryosphere, 6, 1561-1576, 2012.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Maëlle Nodet
Enseignant-chercheur à l'Université Grenoble Alpes, membre du laboratoire de mathématiques appliquées Jean Kuntzmann et de l’équipe AIRSEA d’Inria Grenoble Rhône-Alpes.

Jocelyne Erhel
Directrice de recherche émérite Inria, chercheuse en modélisation et simulation pour les sciences de l'environnement.