
Un algorithme de découpe de gâteau
Pour couper un gâteau en parts égales, on pourrait bien sûr utiliser une règle graduée. Mais le plus souvent, ne disposant que d’un couteau, comment couper le gâteau en 3 sans léser personne ? Eh bien, l’informatique répond à cette question : pour couper en 3, il suffit de savoir couper en 2.
Partager un gâteau rectangulaire
Considérons un gâteau rectangulaire, un quatre-quarts par exemple. Nous allons appliquer une méthode systématique, que les informaticiens appellent un algorithme, pour le partager en deux parties : un tiers d’un côté, deux tiers de l’autre. Pour cela, on commence par le couper en 2 parties égales et on écarte la partie droite (colorée en rouge). Cela signifie qu’on ne la coupera plus et qu’elle appartient à la partie 2/3 que l’on construit. On coupe ensuite la partie blanche en 2 et on écarte la partie gauche (colorée en jaune). Cela signifie qu’on ne la coupera plus et qu’elle appartient à la partie 1/3 que l’on construit. On coupe la partie blanche en 2 et on écarte la partie droite. On coupe la partie blanche en 2 et on écarte la partie gauche. Et ainsi de suite, on continue à couper en 2 la partie blanche restante et à écarter successivement les parties droite et gauche.

Mathématiquement, on ne devrait jamais s’arrêter, puisqu’il faut toujours recouper le morceau blanc du gâteau. En pratique, il devient rapidement impossible de recouper le gâteau, car cette partie est trop petite. Au bout d’un certain nombre de coupes, on s’arrête donc et on « recolle » les morceaux de même couleur. La partie gauche (ici jaune) est très proche du tiers du gâteau. Il reste encore à couper la partie droite (rouge) en 2 pour obtenir une découpe en 3 tout à fait acceptable.

Notez que pour des raisons purement culinaires, cette technique est déconseillée dans le cas d’un mille-feuilles. Mais bien entendu, elle permet de réaliser un gabarit en papier aux dimensions de votre gâteau !
Et si le gâteau est rond ? La même technique peut s’appliquer : on coupe en 2 et on écarte d’un côté ou de l’autre la moitié juste découpée.

Le problème est alors qu’il faut savoir couper un morceau de tarte (un secteur angulaire) en 2, ce qui est un peu plus difficile en pratique que pour un rectangle, car il faut être très précis sur le centre et sur les découpes.
En fait, pour un gâteau circulaire, il existe une méthode plus simple :

- On coupe un rayon.
- On en trouve le milieu et on dessine la perpendiculaire au rayon en ce point (c’est la médiatrice du rayon).
- Les points de rencontre avec les bords du gâteau sont exactement les endroits où l’on doit couper pour obtenir 1/3 du gâteau.
- Reste à couper en 2 la grosse part (en continuant le rayon choisi initialement) et on obtient très facilement 3 parts égales.
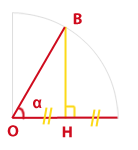
Pourquoi cette technique (appelons-la elle aussi un algorithme) fonctionne-t-elle ? L’explication est basée sur la trigonométrie :
Le triangle OBH est rectangle et OH est égal à la moitié de OB (puisque OB est un rayon).
Donc l’angle α est tel que :
cos(α) = OH/OB = 1/2
Donc α = 60 ° et cette découpe correspond donc à 1/6 du gâteau. En ajoutant le morceau symétrique par rapport au rayon initial, on a donc bien obtenu 1/3 du gâteau soit un secteur angulaire de 120 °.
Mais il est à noter que cette méthode s’adaptera mal si l’on souhaite obtenir un autre nombre de parts.
Pourquoi ça marche ?
Pourquoi donc cet algorithme fonctionne-t-il ?
En fait, il faut revenir aux bases. Nous sommes habitués à l’écriture des nombres en base 10, ce qui correspond au fait que, quand on se déplace vers la gauche, chaque chiffre a une valeur 10 fois supérieure :
2010 = 2 . 103 + 0 . 102 + 1 . 101 + 0
De façon similaire, en base 2, qu’on appelle aussi écriture binaire, chaque chiffre plus à gauche a une valeur 2 fois supérieure à la valeur de son voisin :
10011012 = 1 . 26 + 0 . 25 + 0 . 24 + 1 . 23 + 1 . 22 + 0 . 21 + 1
On note XXXX2 la représentation des nombres en base 2.
Tout nombre entier a une représentation en base 2 et en base 10. Par exemple, 10011012 = 73 et 2010 = 111110110102.
Pour les nombres réels non entiers (avec des chiffres non nuls derrière la virgule), les représentations ne sont pas équivalentes. Un exemple souvent cité est celui de 1/10 = 0,1 qui s’écrit en binaire avec un nombre infini de chiffres.
1/10 = 0,00011001100110011001100110011001100112…
= 0 + 0 . 2-1 + 0 . 2-2 + 0 . 2-3 + 1 . 2-4 + 1 . 2-5 + 0 . 2-6 + 0 . 2-7 + 1 . 2-8 + 1 . 2-9 +…
Revenons à notre algorithme de découpe. On veut couper le gâteau en 3 parts égales, donc le diviser en 3. Regardons l’écriture de la fraction 1/3 en base 2 :
1/3 = 0,010101010102…
La valeur 1/3 représentée en base 2 est donc « 0, » suivi de « 01 » répété infiniment. Cela traduit le fait que 1/3 est la limite de la somme : 2-2 + 2-4 + 2-6 +… c’est-à-dire de la somme 1/4 + 1/16 + 1/64 +…
L’écriture binaire dicte en conséquence les moitiés de part à conserver pour construire 1/3. Remplaçons les chiffres après la virgule : 0 par D et 1 par G, on obtient :
0 1 0 1 0 1 0 1 0 1 0 1 0 1 …
D G D G D G D G D G D G D G …
À chaque fois que l’on rencontre un 0, on met le morceau coupé à droite (partie rouge), il ne fera pas partie du tiers que l’on construit. Quand on rencontre un 1, on met le morceau à gauche (partie jaune), il fera partie du tiers que l’on construit. On continue ainsi à mettre les morceaux successivement à droite et à gauche, jusqu’à ne plus pouvoir couper.
Et si on est plus nombreux ?
L’algorithme précédent s’adapte à un autre nombre de parts. Ainsi, considérons 7 convives. On écrit alors 1/7 en base 2 :
1/7 = 0,00100100100102…
On constate que 1/7 s’écrit « 0, » suivi d’une infinité de « 001 » répétés. Cela donne donc DDGDDGDDGD…

Pour couper en 7 parts, on coupe donc de façon successive en 2 et on met les morceaux à droite, une deuxième fois à droite, puis à gauche, de façon répétée. Une fois la première part obtenue (le premier septième), il faut encore couper le reste en 6, par exemple en le coupant en 2 puis chaque morceau en 3. Cela prend du temps (selon la précision avec laquelle on souhaite obtenir le résultat), mais on parvient à couper le gâteau en 7 parts raisonnablement égales.
Plus généralement, l’algorithme de découpe en n parts est déduit de la représentation binaire de la fraction 1/n.
L’algorithme que nous venons de décrire est un cas particulier de l’algorithme suivant, encore plus général, qui permet d’obtenir une part de taille r, avec r compris entre 0 et 1. Par exemple, pour diviser par 3, c’est-à-dire multiplier par 1/3, on applique cet algorithme avec r = 1/3 :
- Couper en 2.
- Si r < 1/2
donc, en écriture binaire, le premier chiffre après la virgule est 0,
mettre le morceau à droite. - Si r ≥ 1/2
donc, en écriture binaire, le premier chiffre après la virgule est 1,
mettre le morceau à gauche. - Si r ≥ 1/2,
remplacer r par r – 1/2. - Remplacer r par 2 r :
en écriture binaire, cela revient à supprimer le premier chiffre après la virgule. - Recommencer jusqu’à ce que r soit égal à 0 ou qu’on ne puisse plus couper.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
