
Automates cellulaires et phénomènes d’auto-organisation : le rôle de l’aléa
Avez-vous déjà observé une nuée d’oiseaux se former dans le ciel ? En quelques instants, les oiseaux s’élèvent et se rassemblent dans les airs, pour virevolter ensemble de manière parfaitement synchronisée. Et pourtant, il n’y a pas de chef pour orchestrer cette chorégraphie. On peut même supposer que pour ajuster sa direction de vol, chaque oiseau ne dispose que d’une vue partielle et agit donc essentiellement en fonction des mouvements des quelques oiseaux les plus proches de lui. De tels phénomènes d’auto-organisation sont fréquents dans la nature, comme en témoigne aussi la formation de bancs de poissons. À l’échelle cellulaire, la mise en place de certaines structures semble également être régie par des mécanismes similaires, comme l’ont montré des travaux récents portant sur la formation de motifs sur des peaux de lézards.
Les automates cellulaires constituent un modèle informatique simple permettant de mimer ces phénomènes d’auto-organisation. L’objectif est d’extraire des mécanismes élémentaires permettant de mener à de tels comportements. On peut alors espérer pouvoir les reproduire dans des contextes artificiels, pour résoudre des problèmes d’obtention de consensus ou de synchronisation dans des réseaux décentralisés. En effet, de nombreux réseaux informatiques actuels fonctionnent de manière distribuée, sans autorité centrale, et nécessitent la mise en place d’une forme de régulation collective, basée sur des interactions locales.
Automates cellulaires : l’exemple du modèle de formation d’essaims
Dans le modèle des automates cellulaires, on suppose que les entités sont disposées selon une grille régulière, et qu’en chaque cellule de la grille, seul un nombre fini d’états sont possibles. À chaque pas de temps, les états de toutes les cellules évoluent en fonction d’une règle locale qui dépend seulement des états des cellules voisines.
Un automate cellulaire reproduisant la formation d’essaims d’oiseaux a ainsi été étudié par les chercheurs Nazim Fatès, Vincent Chevrier, et Olivier Bouré (Inria et Université de Lorraine) : on suppose qu’en chaque cellule de la grille, pour chacune des quatre directions cardinales (N, S, E, O), il peut y avoir (au plus) un oiseau qui pointe vers cette direction. La règle de mise à jour définissant la dynamique de l’automate cellulaire est alors constituée de deux étapes (cf. Figure 1 ci-dessous) :
- une étape d’interaction au cours de laquelle les oiseaux de chaque cellule sont éventuellement amenés à modifier leur orientation, pour s’aligner davantage avec les oiseaux des cellules voisines,
- une étape de propagation, au cours de laquelle chaque oiseau avance d’une cellule dans la direction retenue.

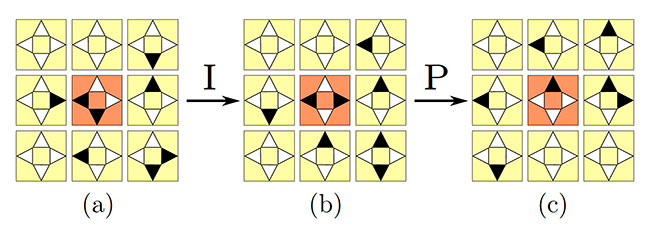
Figure 1 : Décomposition de l’action de l’automate cellulaire en deux étapes : une étape d’interaction (I) et une étape de propagation (P). Les triangles noirs indiquent la présence d’un oiseau. Dans la cellule centrale (orange), il y a initialement deux oiseaux présents. Ceux-ci pointent vers les directions S et O (a). Après l’étape d’interaction, qui possède une composante aléatoire, leurs nouvelles directions sont O et E (b). À l’étape de propagation, les deux oiseaux de la cellule centrale se déplacent respectivement vers les cellules voisines à l’ouest et à l’est, et l’oiseau qui était dans la cellule voisine au sud rejoint la cellule centrale. Figure extraite des travaux de Fatès et al.
Illustration © Sacha Berna
L’étape d’interaction possède une part d’aléa, tandis que l’étape de propagation est déterministe. Un paramètre d’alignement permet d’ajuster l’importance accordée aux orientations des oiseaux voisins lors de l’étape d’interaction : plus il est élevé, plus les oiseaux vont favoriser une réorientation leur permettant de s’aligner avec leurs voisins. En fonction de la densité initiale d’oiseaux sur la grille et de la valeur de ce paramètre d’alignement, les simulations révèlent effectivement la formation d’un ou plusieurs essaims d’oiseaux volant ensemble dans une même direction. De manière assez frappante, en augmentant progressivement le paramètre d’alignement, on constate qu’il existe une valeur critique à partir de laquelle on passe brusquement d’un régime désordonné à un régime où le système réussit à « sélectionner » une direction privilégiée de vol (cf. Figure 2 ci-après). En reprenant la terminologie de physique statistique, on peut parler de « transition de phase ».
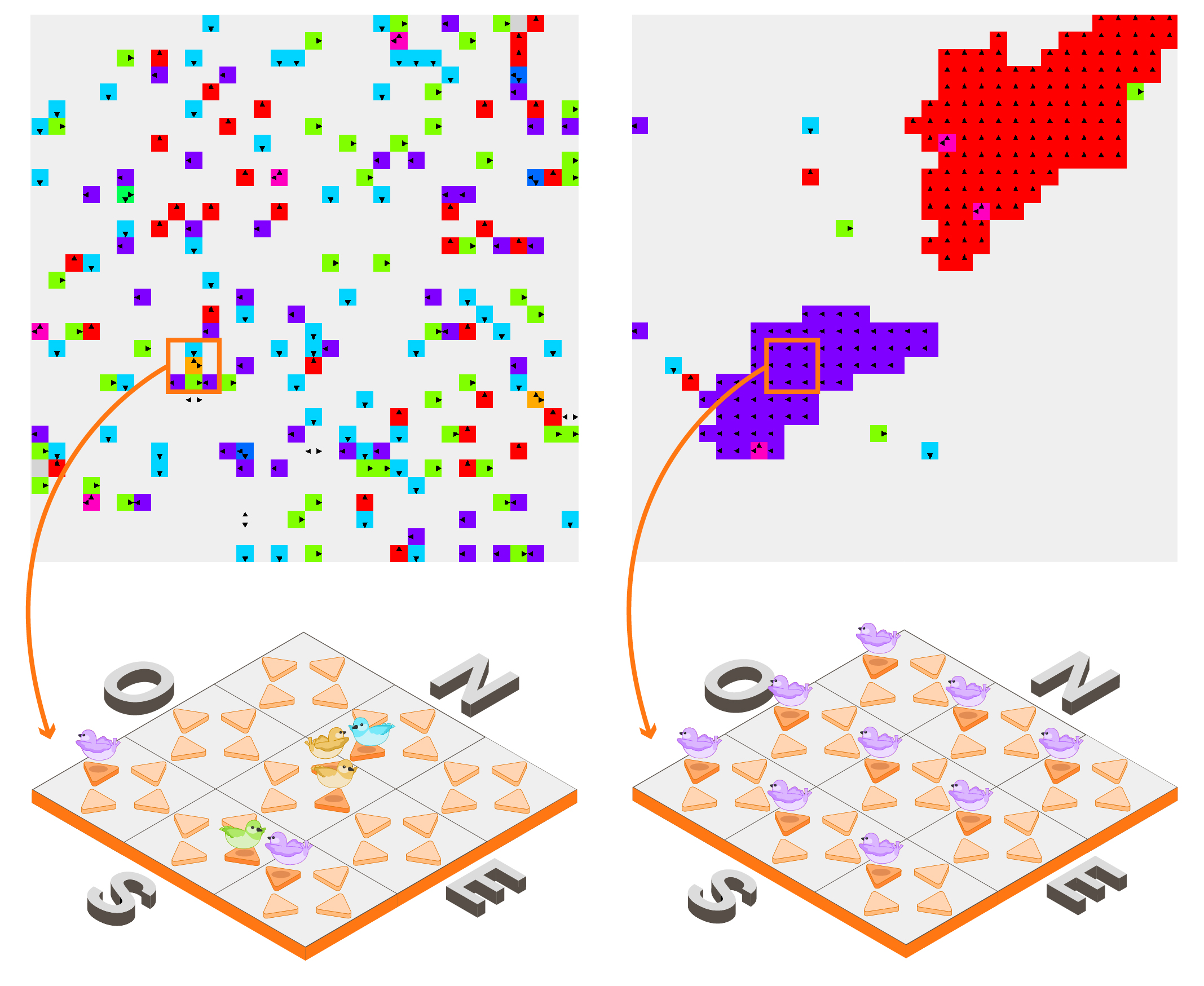
Figure 2 : À partir d’une configuration « désordonnée » (à gauche), lorsque le paramètre d’alignement dépasse un certain seuil, on atteint une configuration « ordonnée » (à droite) composée d’un ou plusieurs essaims évoluant dans la même direction : ici, on constate que deux essaims volant respectivement en direction N et O se sont formés. Chaque couleur correspond à une configuration possible de la cellule : rouge (respectivement bleu clair, vert clair, violet) lorsqu’il y a un unique oiseau pointant vers la direction N (resp. S, E, O), orange (resp. rose, bleu foncé, vert) lorsqu’il y a deux oiseaux pointant vers le NE (resp. NO, SO, SE). Figures réalisées avec le logiciel FiatLux, pour des conditions aux bords périodiques.
Illustration © Sacha Berna
Ce modèle peut sembler bien rudimentaire : les cellules sont supposées être disposées selon une grille parfaitement régulière, les oiseaux ne peuvent voler que dans l’une des quatre directions cardinales (avec un maximum d’un oiseau par direction dans chaque cellule), et le temps est discrétisé, en faisant l’hypothèse que les oiseaux sont tous réglés selon une même horloge leur indiquant quand appliquer la règle de mise à jour. Cependant, malgré ces choix simplificateurs, le modèle reste difficile à étudier analytiquement, et il semble pour le moment hors de portée de déterminer précisément les zones des paramètres pour lesquelles des essaims se forment.
D’un point de vue théorique, il est donc intéressant de concevoir des automates cellulaires encore plus simples menant à une certaine forme d’auto-organisation, et pour lesquels une étude mathématique est possible. Il s’agit alors de résoudre ce qu’on appelle un problème inverse : étant donné un certain comportement, on cherche à exhiber une règle locale, la plus simple possible, permettant d’aboutir à ce comportement.
Dans la suite de cet article, nous allons nous intéresser à deux problèmes inverses, le problème de la synchronisation et le problème de la majorité, en nous intéressant tout particulièrement au rôle que peut avoir le hasard dans la mise en place d’un comportement d’auto-organisation.
Dans les deux cas, nous nous restreindrons à l’étude de configurations finies de dimension 1 : nous supposerons que les cellules sont disposées selon un ruban régulier qui se referme sur lui-même pour former un anneau (on les représente ici en ligne, mais il faut imaginer que la cellule la plus à gauche et celle la plus à droite sont collées). De plus, nous supposerons que chaque cellule ne peut prendre que deux états possibles : l’état bleu et l’état blanc. Nous verrons que ce cadre extrêmement simplifié permet déjà d’exhiber des phénomènes complexes, qui soulèvent des défis théoriques.
Le problème de la synchronisation
Le problème de la synchronisation consiste à chercher un automate cellulaire tel qu’au bout d’un certain temps, les cellules prennent alternativement toutes l’état blanc, puis toutes l’état bleu, puis toutes l’état blanc, etc. Il s’agit ainsi de donner une même consigne à toutes les cellules, consistant à choisir à chaque pas de temps une couleur en fonction des couleurs de leurs voisines, de manière à ce qu’elles atteignent toutes un régime où elles alternent de manière parfaitement synchrone entre l’état blanc et l’état bleu. Le comportement souhaité peut ainsi être interprété comme une réplique numérique de la synchronisation de métronomes : de même que des métronomes posés sur une planche finissent par se synchroniser pour battre exactement selon le même tempo, on voudrait que quelle que soit la taille de l’anneau et la configuration initiale, l’automate cellulaire permette aux cellules d’atteindre une synchronisation parfaite de clignotement entre blanc et bleu.
En testant de nombreux automates cellulaires à l’aide de simulations intensives, des travaux ont permis d’exhiber des règles locales ayant de très bonnes propriétés statistiques : pour la plupart des conditions initiales de l’anneau, les cellules parviennent à se synchroniser. Cependant, quel que soit l’automate cellulaire retenu, des recherches exhaustives mettaient en évidence des configurations initiales ne permettant pas d’atteindre la synchronisation des cellules. Ceci a été confirmé par un résultat théorique : en fait, il n’existe pas d’automate cellulaire déterministe permettant de résoudre parfaitement le problème de la synchronisation, pour toute taille d’anneau et pour toute configuration initiale !
Une démonstration de ce résultat, due à Gaétan Richard (maître de conférences en informatique à l’Université de Caen), consiste à montrer que pour tout automate cellulaire, il existe une configuration que l’automate cellulaire fait tourner indéfiniment sur l’anneau. À partir d’une telle configuration, on ne pourra donc jamais atteindre un clignotement entre blanc et bleu. Pour simplifier l’explication, considérons un automate cellulaire tel que pour toute position \(k\), si les cellules d’indices \(k\)−1, \(k\), \(k\)+1 sont respectivement dans l’état \(x\), \(y\), \(z\) au temps \(t\), alors au temps \(t\)+1, la cellule \(k\) prend l’état \(f\)(\(x\), \(y\), \(z\)). La fonction \(f\) est la règle locale de l’automate cellulaire. Encodons l’état blanc par \(0\) et l’état bleu par \(1\), et définissons successivement les valeurs :

Comme les \(x\)n ne peuvent prendre que deux valeurs, \(0\) ou \(1\), il existe forcément deux entiers \(m\) < \(n\) tels que \(x\)m\(x\)m+1\(x\)m+2 = \(x\)n\(x\)n+1\(x\)n+2. Considérons alors la configuration \(x\)m\(x\)m+1\(x\)m+2…\(x\)n−2\(x\)n−1, recollée sur elle-même pour former un anneau : sous l’action de l’automate cellulaire, cette configuration ne fait que tourner autour de l’anneau en se translatant de deux cases à chaque étape.
On peut cependant assouplir un peu le problème en autorisant également des solutions probabilistes. Pour choisir sa nouvelle couleur, chaque cellule regarde alors les couleurs de ses voisines et, selon ce qu’elle observe, elle a aussi la possibilité d’effectuer un tirage à pile ou face pour trancher. Dans ce nouveau contexte, il existe une règle très simple permettant de répondre parfaitement au problème de la synchronisation. Celle-ci est la suivante : chaque cellule regarde sa propre couleur et la couleur de sa voisine de droite ; si les couleurs coïncident, la cellule change de couleur, dans le cas contraire, elle tire à pile ou face pour choisir sa nouvelle couleur. Au cours de l’évolution, les frontières entre les cellules blanches et les cellules bleues se déplacent en suivant une marche aléatoire et les plages de cellules de même couleur finissent pas fusionner, de sorte qu’on peut montrer que cette règle permet avec probabilité \(1\) (on dit aussi « presque sûrement ») de synchroniser toutes les cellules.
Ici, on voit donc que l’introduction d’aléa ouvre de nouvelles possibilités et s’avère être un ingrédient essentiel pour atteindre le comportement d’auto-organisation souhaité.

Figure 3 : Résolution du problème de la synchronisation grâce à un automate cellulaire probabiliste : la configuration initiale est représentée en bas et le temps va de bas en haut. Lorsque deux frontières entre des plages de couleurs différentes se rencontrent, la plage centrale fusionne avec ses deux voisines. Après davantage d’itérations, il ne reste plus qu’une seule plage, qui clignote entre blanc et bleu. Illustration © Sacha Berna.
Le problème de la majorité
Dans cette partie, on suppose que l’anneau contient un nombre impair de cellules. Le problème de la majorité consiste alors à trouver un automate cellulaire tel que, si la configuration initiale contient une majorité de cellules bleues, toutes les cellules finissent par se figer sur l’état bleu, tandis que si la configuration initiale contient une majorité de cellules blanches, les cellules se figent sur l’état blanc. Il s’agit ainsi d’un problème d’obtention de consensus : quelle que soit la configuration initiale, on souhaite que l’automate cellulaire permette d’atteindre un état où toutes les cellules sont dans la couleur qui était majoritaire au départ. La difficulté est que toutes les cellules jouent le même rôle : il n’y a pas de chef capable de regarder la configuration de haut pour compter le nombre de cellules de chaque couleur. De plus, les cellules ne disposent d’aucune mémoire, elles peuvent seulement prendre à chaque instant l’état blanc ou l’état bleu. Ce problème est aussi connu sous le nom du problème de la classification de la densité, le terme de densité faisant référence à la fréquence d’apparition de chaque couleur dans la configuration.
À nouveau, certains automates cellulaires permettent d’atteindre le bon consensus pour une très grande majorité de configurations initiales, mais on peut montrer qu’il n’existe aucun automate cellulaire permettant de résoudre parfaitement le problème. Et cette fois-ci, les automates cellulaires probabilistes n’offrent pas non plus de solution parfaite ! Dans un article de 2011, le chercheur Nazim Fatès a néanmoins proposé de combiner de manière aléatoire une règle locale de la majorité avec la règle trafic, qui déplace les couleurs dans une direction donnée. En ajustant les paramètres de l’automate cellulaire probabiliste ainsi construit, on peut résoudre le problème avec une précision arbitrairement grande, c’est-à-dire atteindre le consensus sur l’état majoritaire avec une probabilité aussi proche de \(1\) que l’on souhaite (et ce, au prix d’un allongement du temps de réponse du système). L’aléa nous permet donc une nouvelle fois de faciliter l’auto-organisation !
Pour préciser le fonctionnement de cette solution probabiliste, commençons par introduire l’automate cellulaire trafic, qui imite le mouvement de véhicules le long d’une route : les cellules bleues représentent des véhicules, et à chaque pas de temps, tous les véhicules qui ont un espace libre devant eux avancent d’une position vers la droite, comme illustré ci-dessous.

Cet automate cellulaire préserve le nombre de cellules de chaque couleur, et a la propriété de « dissoudre » les bouchons autant que possible : si initialement, il y a une majorité de cellules blanches, alors au bout d’un certain temps, on ne verra plus jamais deux cellules bleues consécutives (et de même, s’il y a initialement une majorité de cellules bleues, alors au bout d’un certain temps, on ne verra plus jamais deux cellules blanches consécutives).
Introduisons également l’automate cellulaire de la majorité : pour celui-ci, la nouvelle couleur de la cellule \(k\) est la couleur qui était majoritaire parmi les couleurs des cellules \(k\)−1, \(k\), \(k\)+1. Un exemple d’évolution de cet automate cellulaire est également représenté ci-dessous.

On considère la combinaison suivante de ces deux automates cellulaires : à chaque instant, chaque cellule choisit avec probabilité \(p\) d’appliquer la règle de la majorité, et avec probabilité 1−\(p\) d’appliquer la règle trafic. Si \(p\) est suffisamment petit, alors avec grande probabilité, l’automate commence par espacer au maximum les cellules de même couleur, puis l’action de la règle majorité permet d’atteindre le consensus sur la couleur majoritaire, comme illustré sur la Figure 4 ci-dessous.
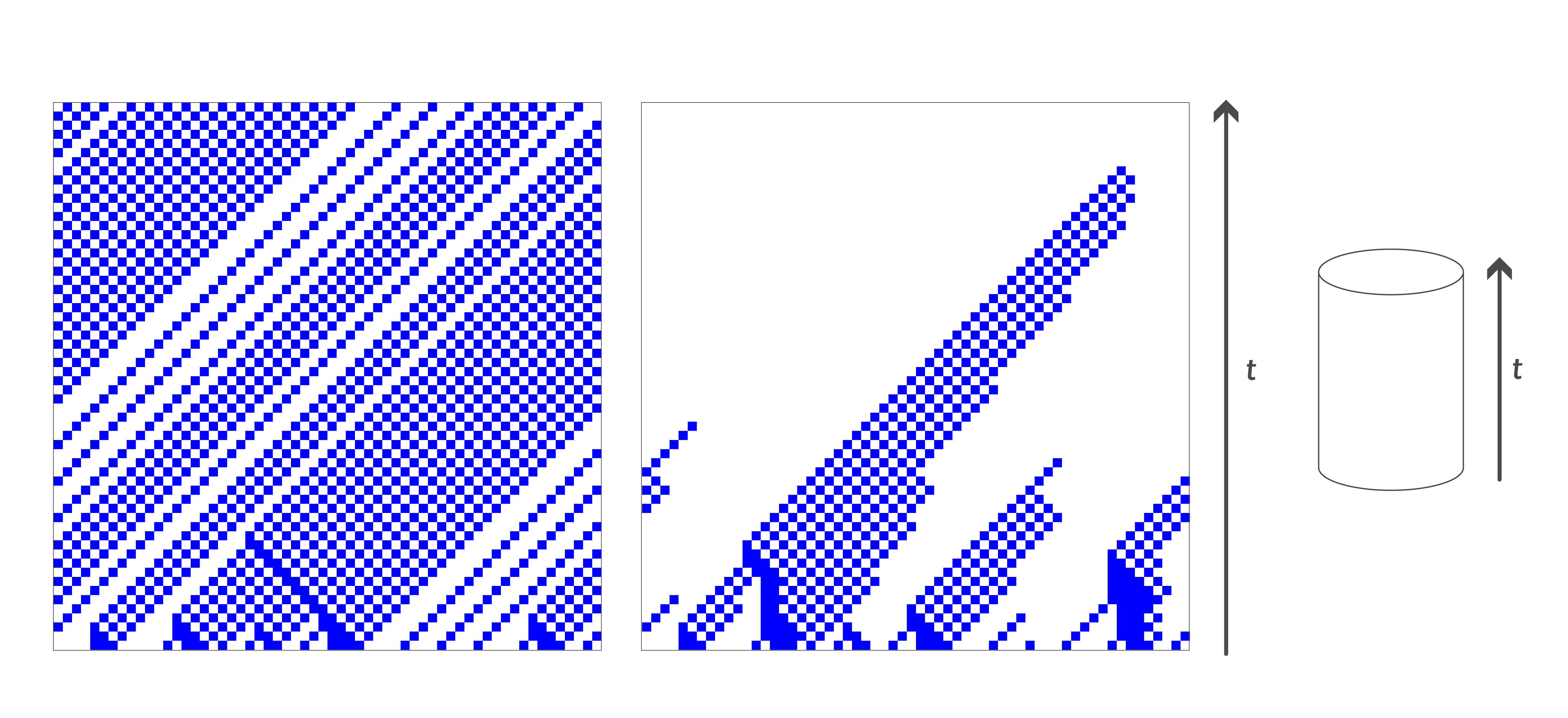
Figure 4 : À partir d’une même configuration initiale représentée en bas des diagrammes, et qui comporte une majorité de cellules blanches, l’image de gauche montre l’évolution de l’automate cellulaire trafic, et celle de droite l’évolution observée lorsqu’on combine cet automate cellulaire avec la règle de la majorité. À gauche, on observe que la règle trafic dissout rapidement les petits bouchons bleus pour atteindre un comportement périodique où il n’y a plus de bouchons. À droite, les applications de la règle majorité permettent de faire diminuer progressivement le nombre de cellules bleues : à partir du moment où il n’y a plus deux cellules bleues consécutives, les applications aléatoires de la règle majorité ne peuvent que réduire le nombre de cellules bleues, en faisant disparaître celles qui ont deux cellules blanches devant elles.
Illustration © Sacha Berna.
Informatique et hasard
Informatique et hasard ne font pas toujours bon ménage. En particulier, la plupart des systèmes informatiques sont bien peu robustes à des perturbations : le moindre petit changement peut entraîner un dysfonctionnement complet. Ainsi, le réseau ferroviaire d’une ville de plusieurs millions d’habitants a été récemment paralysé par l’obsolescence d’un logiciel. À l’inverse, les organismes vivants possèdent tous une certaine capacité à se réparer lorsqu’ils sont soumis à une perturbation. Dans son article fondateur de 1952 (The chemical basis of morphogenesis), Alan Turing évoquait l’exemple saisissant de l’hydre, un petit animal aquatique capable de se régénérer après avoir été tronqué ou même réduit à un amas informe de cellules. De manière plus générale, on peut même penser que le hasard est un élément essentiel permettant le développement des organismes et leur auto-organisation. Peut-être y a t-il là une source d’inspiration possible pour mieux concilier informatique et hasard ?
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Irène Marcovici
Maîtresse de conférences dans l’équipe de probabilités et statistique de l’Institut Élie Cartan de Lorraine (Université de Lorraine).
