
Des espèces en nombre
Le 12 décembre 1999, 6 h du matin, la mer est forte au large de Penmarc’h (Finistère). Le pétrolier Erika, transportant 37 000 tonnes de fioul lourd, lance un appel de détresse. Il coulera quelques heures plus tard. La marée noire qui suivit ce naufrage marque encore de ses traces de nombreuses côtes bretonnes : 150 000 oiseaux marins meurent, des phoques, des dauphins, des poissons, les algues et le micro-plancton sont largement contaminés par les résidus cancérigènes d’hydrocarbures… C’est tout un écosystème qui vacille en quelques jours.
Peut-on optimiser une stratégie de dépollution pour limiter l’impact de la marée noire sur les populations animales ou végétales les plus fragiles ? Quelle a été l’influence à long terme de cette marée noire sur les écosystèmes de la région ? Il est très difficile de répondre à de telles questions sans avoir recours à des modèles de prédiction et de simulation de la dynamique des populations. Ces modèles sont aujourd’hui, comme ceux des prévisions météorologiques, extrêmement complexes au niveau mathématique et informatique ; ils nécessitent de gros moyens de calcul. Cependant, ils sont fondés sur des principes simples, élaborés bien avant l’invention des ordinateurs.
Comment se caractérise une population ?
Une population animale ou végétale est formée d’individus d’une même espèce qui interagissent entre eux, notamment au moment de la reproduction. Par définition, les individus d’une même population ont tous la possibilité de se rencontrer. C’est ce qui distingue la notion de population de celle d’espèce. Cette dernière, très générale, rassemble tous les individus interfertiles, même si ceux-ci n’ont jamais la possibilité de se croiser. Les espèces sont donc très souvent structurées en populations qui, à cause de l’éloignement géographique ou de l’hétérogénéité de leur habitat, n’interagissent pas nécessairement entre elles. La population est l’unité d’étude dans de nombreux domaines des sciences de la vie.
En particulier, la dynamique des populations s’intéresse aux changements incessants que subissent les populations, du fait de la disparition d’individus par mortalité ou émigration et de l’apparition de nouveaux individus par reproduction ou immigration. Elle étudie également les interactions entre populations d’une même espèce ou d’espèces différentes, comme la compétition pour l’espace ou l’accès à la ressource, la symbiose ou encore le parasitisme.
La chaîne (ou le réseau) trophique est l’ensemble des relations qui s’établissent entre les espèces selon la façon dont elles se nourrissent. Ces relations assurent la circulation de la matière organique et de l’énergie au sein de l’écosystème. Les éléments constitutifs de l’écosystème peuvent ainsi être regroupés en trois grandes catégories :
- les producteurs primaires (comme les algues microscopiques d’eau douce par exemple) qui rassemblent le phytoplancton (végétaux qui produisent grâce à la photosynthèse la plus grande part de l’oxygène que nous respirons), le périphyton (association d’algues, bactéries et champignons) et les macrophytes (plantes aquatiques) ;
- les consommateurs primaires, eux-mêmes producteurs secondaires, qui sont exclusivement herbivores (insectes, crustacés, mollusques et poissons) ;
- et les consommateurs secondaires ou prédateurs (les oiseaux par exemple) qui peuvent être piscivores, insectivores, carnivores, voire charognards. L’homme, qualifié de superprédateur, est souvent le dernier maillon de la chaîne.
La compréhension de ces processus dynamiques complexes se trouve aujourd’hui facilitée par divers modèles mathématiques. Ces modèles permettent de simuler l’évolution des populations et de prévoir les effets d’une perturbation de leur environnement. Quel que soit le modèle choisi, celui-ci reste une représentation simplifiée du monde réel et se fonde sur des hypothèses simplificatrices plus ou moins réalistes. Il est écrit sous forme de systèmes d’équations. Selon que l’on considère le temps et l’espace comme des variables continues (qui prennent toute valeur réelle dans un intervalle donné) ou discrètes (qui prennent des valeurs dans un ensemble fini ou dénombrable), on peut distinguer différentes catégories d’équations :
- les équations aux dérivées partielles (temps et espace continus) ;
- les équations différentielles récurrentes (temps et espace discrets) ;
- les équations différentielles ordinaires (temps continu, espace discret).
En première approximation, l’environnement (l’espace) est souvent considéré comme homogène. La seule variable indépendante reste alors le temps.
Une équation différentielle fait intervenir des inconnues qui ne sont pas des nombres, mais une fonction réelle y(x) dépendante de la variable réelle x, et ses dérivées successives y’, y », … L’ordre d’une équation différentielle correspond au degré maximum de dérivation dans l’équation. Par exemple, y’ = r y est une équation différentielle d’ordre 1.
Résoudre une équation différentielle consiste donc à chercher toutes les fonctions solutions y(x) qui la vérifient. Les solutions d’une équation différentielle dépendent d’un nombre de paramètres égal à l’ordre de l’équation. La valeur de ces paramètres dépend du choix des conditions initiales, c’est-à-dire de l’état du système à un moment donné. Par exemple, les solutions de l’équation y’ = r y sont de la forme y(x) = y0 erx avec y0 = y(0).

Portrait du mathématicien italien Fibonacci (© Fototeca / Leemage).
La complexité des modèles mathématiques croît avec la quantité de détails que l’on veut prendre en compte dans la description du processus. Ainsi, certains modèles ne nécessitent guère plus qu’un papier et un crayon pour être appréhendés, tandis que d’autres engendrent parfois plusieurs jours de calcul sur des grappes d’ordinateurs travaillant en parallèle.
L’utilisation de modèles mathématiques en sciences de la vie a connu un engouement à partir du milieu du XXe siècle. On peut toutefois dater de 1202 le tout premier modèle proposé en dynamique des populations. On le doit à Leonardo Pisano, mathématicien italien plus connu sous le pseudonyme de Fibonacci (1175-1250), qui dans son Liber abaci a tenté de décrire la croissance d’une population de lapins, donnant ainsi naissance à la fameuse suite de Fibonacci.
Étudier la dynamique d’une population isolée
Un bond de plusieurs siècles dans l’histoire nous amène aux travaux du pasteur anglican et économiste britannique Thomas Robert Malthus (1766-1834) qui prédit à cette époque d’inévitables catastrophes démographiques si les naissances ne sont pas contrôlées dans les populations humaines. Il considère qu’une population croît de manière exponentielle ou géométrique (2, 4, 8, 16, 32…) tandis que les ressources augmentent de manière linéaire ou arithmétique (1, 2, 3, 4, 5…). Implicitement, le modèle de Malthus repose sur des hypothèses très simplificatrices :
- l’accroissement de la population est seulement le résultat d’un équilibre entre les naissances et les décès, les processus de migration sont négligés ;
- l’accroissement absolu de la population (∆N, exprimé en effectif) est proportionnel à l’effectif N de la population et à l’intervalle de temps ∆t pendant lequel on le mesure (∆N = r N ∆t) ;
- tous les individus sont supposés équivalents et représentés par une moyenne.
La dynamique de la population se trouve alors entièrement résumée dans le paramètre r, appelé « taux de croissance malthusien », qui résulte de la différence entre le taux de natalité et le taux de mortalité naturels de la population.
La dynamique des populations est également marquée, au début du XIXe siècle, par les travaux du mathématicien belge Pierre-Henri Verhulst (1804-1849) qui, par opposition au modèle de croissance exponentielle de Malthus, propose de modéliser la dynamique des populations animales par une fonction logistique, dont la courbe représentative est une courbe en forme de « S ». Ce modèle logistique considère que, dans la nature, les populations s’auto-régulent pour faire face à une limitation de leur environnement soit par l’espace, soit par la ressource. Ainsi, les taux de natalité et de mortalité naturels dépendent de la densité même d’individus au sein de la population.
Verhulst modélisa ce phénomène en introduisant deux relations linéaires dans le modèle de Malthus : une croissante entre la natalité et la densité, et une seconde décroissante entre la mortalité et la densité. Tant que le nombre d’individus reste faible, la population croît avec un taux de type malthusien ; dès que le nombre d’individus devient trop important, l’évolution de la population tend alors à s’infléchir pour atteindre un équilibre. Cette « capacité limite » correspond à la taille maximum que peut atteindre la population si les conditions environnementales restent inchangées.

Le modèle de Verhulst : courbe de croissance logistique et boîte de Petri (© Inserm / Photo Michel Depardieu).
La dynamique des populations étudie l’évolution numérique des populations d’êtres vivants, des hommes comme des bactéries. Par exemple, ces études permettent d’évaluer l’impact d’une pollution sur le nombre d’individus d’une population.
Les biologistes étudient le développement de populations bactériennes dans les fameuses boîtes de Petri. La croissance d’une population y est tout d’abord de nature exponentielle : à tout instant, son accroissement est proportionnel à son effectif, ce qui se traduit mathématiquement par l’équation différentielle dN(t)/dt = rN(t), où N(t) est l’effectif de la population à l’instant t et r le taux de croissance intrinsèque.
Mais une telle croissance exponentielle ne peut se poursuivre sur un substrat limité. Pour rendre compte de ce ralentissement, l’équation différentielle précédente doit être complétée par un terme dit de « freinage », pour s’écrire dN/dt = rN (1 – N/K) : quand N croît et tend vers K, 1 – N/K tend vers 0 et la croissance se ralentit de façon asymptotique ; K est donc la « capacité limite », la limite dans le temps de l’effectif de la population. Tout environnement étant par nature limité, il n’est pas étonnant que ce type de croissance, dite « logistique », s’observe dans de très nombreux cas.
Plus tard, des modèles concurrents au modèle logistique ont été proposés, comme celui de Monod (1942) qui décrit l’évolution au cours du temps de la biomasse du phytoplancton dans la chambre d’un chémostat (appareil dans lequel sont cultivés les organismes en laboratoire) en fonction de la concentration en substrat.
Quand différentes populations (issues d’espèces différentes) interagissent, la dynamique de chacune est affectée par les effectifs des autres. Elles forment une cascade de populations en interaction qui constitue une communauté, appelée « chaîne trophique ». Les relations possibles entre espèces d’une même chaîne trophique se classent en trois catégories principales : la relation proie-prédateur, la relation de symbiose mutualiste et la relation de compétition.
Étudier la dynamique de populations en interaction
Le plus célèbre des modèles de dynamique de deux populations en interaction est celui de Lotka-Volterra. Il fut proposé indépendamment par Alfred James Lotka (mathématicien et statisticien américain) en 1925 et Vito Volterra (mathématicien et physicien italien) en 1926, afin d’expliquer l’évolution par oscillations du niveau des pêches de sardines et de requins dans la mer Adriatique depuis 1827. Dans ce modèle, les prédateurs prospèrent lorsque les proies sont nombreuses, mais finissent par épuiser leurs ressources et commencent à décliner. Lorsque la population de prédateurs a suffisamment diminué, les proies se reproduisent et leur population augmente à nouveau.
Cette dynamique se poursuit ainsi en un cycle de croissance et déclin. De la même façon, les variations cycliques des populations de lièvres des neiges et de lynx suivies au Canada depuis 1825 ont été modélisées à l’aide du modèle de Lotka-Volterra.

Le modèle de Lotka-Volterra – Le lynx prédateur du lièvre (© ImageSource / age fotostock).
Les nombreuses données de terrain collectées sur les populations de lynx et de lièvres des neiges ont permis d’établir un modèle mathématique, un système d’équations, permettant d’étudier l’interaction entre populations de proies et de prédateurs.
En l’absence de prédation, les prédateurs, d’effectif P, meurent (- mP) et les proies, d’effectif N, croissent sans limite selon un modèle de Malthus (rN). À chaque rencontre parmi les NP possibles, un prédateur peut manger sa proie, selon ω l’efficacité de la prédation ; e est le taux de conversion de la biomasse de proie en biomasse de prédateur.
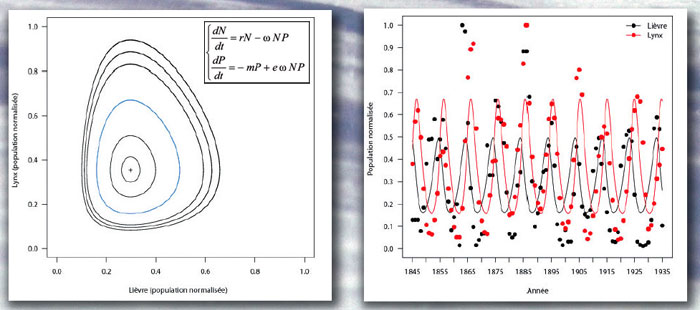
À partir des données des registres de trappeurs du Canada, normalisées par rapport à la valeur maximale observée, on estime : r = 0,53 an – 1, m = 1,83 an – 1, ω = 1,49 an – 1 et e = 1,87. Par simulation, on obtient (à droite) l’évolution au cours du temps des populations de lièvres (courbe noire) et de lynx (courbe rouge) superposée aux points expérimentaux ; et le « portrait de phase » (à gauche) pour suivre l’évolution simultanée des lièvres (axe horizontal) et des lynx (axe vertical) au cours du temps ; chaque courbe correspond à une condition initiale différente, la bleue à N(0) = 0,49 et P(0) = 0,43.
Pour aller plus loin : un article scientifique de J.-R. Lobry à télécharger en PDF.
Des modèles plus complexes pour se rapprocher de la réalité
Les modèles évoqués plus haut relèvent tous du champ des mathématiques dédiées aux équations différentielles ordinaires. La population est toujours considérée comme une entité, qui évolue dans un environnement homogène. Cela suppose implicitement, par exemple, que le taux de natalité est considéré comme constant pour tous les individus. Or ce taux dépend évidemment de l’âge des individus ou de leur stade de développement. La richesse des mathématiques offre d’autres approches de la dynamique des populations, qui prennent en compte cette structuration interne de la population en classes (classes d’âge et de taille, stades de développement…) et pour décrire un processus dynamique spatialisé.
Ainsi, les modèles matriciels de population ou modèles de Leslie (1945) s’avèrent très efficaces. Ces modèles, très largement et depuis longtemps utilisés dans le domaine de l’écologie des populations, décrivent les transferts d’individus d’une classe à la suivante, sur la base du cycle de vie de l’espèce étudiée. L’épidémiologie utilise un découpage analogue en classes (on parle de modèles à compartiments) pour étudier l’évolution temporelle simultanée de la dynamique d’individus sains (S), infectés (I), éventuellement immunisés (R), voire porteurs sains d’un virus. Le but est de comprendre comment une maladie peut soudainement se développer puis disparaître sans s’étendre à toute la communauté, ce que l’on a observé dans d’innombrables épidémies au cours des siècles. Le premier modèle de propagation d’épidémies, connu sous le nom de modèle SIR, naît en 1927, grâce à William Ogilvy Kermack, médecin en santé publique, et Anderson Gray McKendrick, biochimiste, sous la forme d’un système d’équations différentielles ordinaires couplées. Des versions plus sophistiquées ont ensuite inclus d’autres processus comme l’immigration ou le vieillissement de la population.
Modéliser pour prédire et protéger l’environnement
Les activités humaines induisent de nombreuses perturbations sur les écosystèmes. On peut penser à l’impact, sur les populations de poissons de rivière, des centrales hydrauliques, de l’usage intensif des pesticides ou encore des dérivés de l’industrie du pétrole qui, en agissant comme des hormones sexuelles, sont responsables de la féminisation des poissons. Il devient indispensable d’acquérir une meilleure connaissance de tous les facteurs susceptibles de perturber les organismes vivants (leur croissance, leur fertilité, leurs comportements), couplée à l’étude de leurs effets sur les différents niveaux d’organisation biologique (individu, population, communauté). Ces perturbateurs peuvent être physiques (température, débit de l’eau…), chimiques (métaux lourds, résidus médicamenteux…) ou biologiques (toxines, virus…). Le développement de modèles mathématiques à visée prédictive apparaît donc nécessaire pour une meilleure gestion de l’environnement dans la perspective d’un développement durable.
Livres
- Bacaër N., Histoire de mathématiques et de populations, coll. « Le sel et le fer », Cassini, 2009.
- Le Hir P., « L’alarmante pollution de l’eau par les médicaments », Le Monde, février 2009.
- Pavé A., Modélisation en biologie et en écologie, Aléas, Lyon, 1994.
Sites web
- Cours de génétique des populations : en PDF
- MathSV, outils pour la biologie
- Une épidémie mise en équations, article paru dans la revue La Recherche n°335, octobre 2000.
Cet article est paru dans la revue DocSciences n°8 Le numérique et les sciences du vivant, éditée par le CRDP de l’Académie de Versailles en partenariat avec l’Inria.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Sandrine Charles
Maître de conférences, université de Lyon et université Lyon 1, laboratoire de Biométrie - Biologie évolutive (UMR CNRS 5558).

Hubert Charles
Maître de conférences, université de Lyon, INSA de Lyon, laboratoire de Biologie fonctionnelle, Insectes et interactions (UMR INRA 203).