Enigma

Marian Rejewski (1905-1980)
Ce mathématicien n’eut pas conscience, d’abord, que sa découverte allait contribuer à précipiter la fin du Troisième Reich. Il est le seul des trois grands cryptologues polonais à être rentré en Pologne après la fin de la guerre. Il y retrouva sa femme et ses deux enfants.

Jerzy Rózycki (1909-1942)
Travailla pendant la guerre dans des centres secrets de cryptologie en France et en Algérie. Séparé de sa femme et de son enfant de quelques mois, lors du bombardement de Varsovie, Jerzy Rózycki périt le 12 janvier 1942 dans le naufrage du bateau « Lamoricière » au large de l’Angleterre.

Henryk Zygalski (1907-1978)
Mathématicien et pianiste amateur. Après la guerre, il demeura en Grande-Bretagne, où il travailla dans un collège polonais. Il finit ses jours à Plymouth.

Trois rotors placés sur leur axe.

Un réflecteur de type B.

Tableau des connexions.
Photos © Tom Perera – Musée virtuel d’Enigma.

Le cœur de l’Enigma était constitué de trois rotors de chiffrement, positionnés sur un axe commun. Chacun des rotors avait la forme d’un cylindre de métal, avec les 26 lettres de l’alphabet gravées sur sa circonférence ; il était en outre muni d’un anneau en ébonite, possédant d’un côté des plots électriques fixes et, de l’autre, des plots à ressorts. Le cylindre pouvait être positionné librement par rapport à l’anneau. Les rotors pouvaient être installés sur l’axe en configurations différentes, chacun effectuant ses rotations indépendamment des deux autres.

En quoi consistait le processus du chiffrement ? À chaque fois que l’on pressait une lettre, le rotor droit tournait d’un cran (1/26^e de sa circonférence). Les deux autres rotors étaient aussi mis en mouvement : la clé décidait de combien de crans chacun devait tourner. En déterminant le positionnement des rotors et le mode des rotations, la clé indiquait la lettre codée qui correspondrait à la touche enfoncée.

Le système des rotors était encore complété par le réflecteur. Après être passé par le réflecteur, le signal électrique traversait les rotors en sens inverse (la lettre à coder était ainsi envoyée une nouvelle fois à travers les trois rotors, de sorte qu’elle subissait six transformations).

Par ailleurs, la séquence des lettres pouvait être modifiée par le tableau de connexions, qui permutait les lettres connectées deux à deux.

Le réflecteur assurait la réversibilité du chiffrement, si bien que la même machine pouvait servir à coder et à décoder le message. La connaissance de la clé permettait d’inverser le processus du chiffrement ; la séquence de lettres apparemment insensée restituait le message d’origine.

Ce fut toutefois ce même réflecteur qui s’avéra pernicieux pour la sécurité du système : car par exemple, jamais une lettre du message initial ne fut codée par la même lettre (un « e » ne fut jamais codé « e », etc.). Cette régularité facilita la rupture du code.

Le décryptage a été aussi facilité par le fait que les chiffreurs devaient répéter une série de lettres deux fois en début de message.

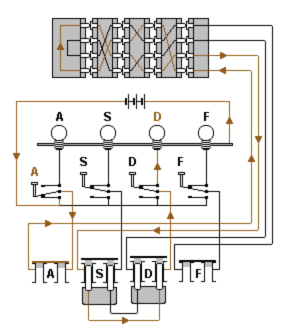
Schéma de fonctionnement d’Enigma, d’après les plans originaux. (source : wikipedia)
À chaque fois qu’une lettre est pressée (ici le A), un circuit électrique se ferme, de sorte que le signal émis, passant par le tableau des connexions, parvient aux rotors de chiffrement. Le signal électrique traverse les rotors pour arriver au réflecteur. Celui-ci renvoie le signal en sens inverse, à travers les rotors, jusqu’au tableau de connexions. Le signal parvient finalement à l’ampoule qui s’allume pour éclairer la lettre résultat (ici le D).

Une permutation est une fonction mathématique qui opère d’un ensemble quelconque dans le même ensemble, et qui est bijective, c’est-à-dire que les images respectives, par une permutation, de deux objets différents, ne peuvent pas être identiques. Par une permutation, des objets, symboles ou autres, sont échangés entre eux.

La théorie des permutations est sous-jacente à la théorie des groupes, qui propose des résultats de base pour n’importe quelle opération mathématique associée à un ensemble sur lequel elle fonctionne, pourvu que cette opération vérifie certaines propriétés. L’opération qui nous intéresse ici est la composition, qui opère sur l’ensemble des permutations possibles d’un ensemble donné, ici l’alphabet de 26 lettres.

Chaque partie de la machine Enigma opère une permutation. La lettre obtenue est donc l’image, par la permutation qui est la composition de ces différentes permutations, de la lettre tapée. Du fait en particulier de la rotation des rotors, les permutations, et donc leur composition, sont différentes pour la prochaine lettre tapée.

Connaissant le fait que les chiffreurs répétaient deux fois en début de message une série de 3 lettres, Marian Rejewski a pu établir, pour chaque message intercepté dans une journée, un lien entre deux lettres (la 1^e et la 4^e par exemple) qui correspondaient à la même lettre de départ (cette lettre elle-même restant inconnue). L’ensemble des paires de 1^e et 4^elettres des messages d’une journée forment une permutation, qui est la composition des deux permutations, inconnues, ayant donné pour résultat chacune des séries de lettres. Il en va de même pour la 2^e et la 5^e, ainsi que pour la 3^e et la 6^e lettres. Marian Rejewski a ainsi obtenu, pour chaque jour, 3 permutations des 26 lettres.

Cherchant à classifier les permutations obtenues, il a alors étudié les chaînes présentes dans ces permutations, en notant la longueur de chacune de ces chaînes.

Par exemple, considérant la permutation
ABCDEFGHIJKLMNOPQRSTUVWXYZ
FQHPLWOGBMVRXUYCZITNJEASDK
on peut noter que le A correspond avec le F, puis le F avec le W, puis le W avec le A, ce qui constitue la chaîne AFWA. De même, on obtient les chaînes BQZKVELRIB, CHGOYDPC et JMXSTNUJ. Cette permutation comporte donc une chaîne de 3 liens, deux de 7 liens et une de 9 liens. (Cet exemple est emprunté à Simon Singh, Histoire des codes secrets.)

Cette astuce a permis à Marian Rejewski de ne pas tenir compte du tableau des connexions, car il a pu montrer que le nombre de chaînes et leur longueur n’étaient pas modifiés par les échanges effectués au niveau de ce tableau.

À l’aide d’une réplique de la machine Enigma, il a alors pu faire établir un répertoire des permutations induites par chacune des positions de départ possibles des rotors, soit 26³x6=105456 possibilités.

Une fois ce répertoire établi, il suffisait de noter chaque jour le nombre et la longueur des chaînes présentes dans les permutations déduites des messages interceptés, puis de trouver dans le répertoire la ou les clés correspondant à ces caractéristiques.

Il restait alors encore à deviner les connexions du tableau à partir du message partiellement décodé.

Sur le web, on trouve de nombreux sites consacrés à Enigma, la plupart en anglais.

Voir en particulier :

• La page d’Andy Carlson qui, en complément de son applet, résume l’histoire d’Enigma et propose quelques références ;
• Le site The German Enigma Cipher Machine – History of Solving, qui donne des informations détaillées et recense de nombreux liens ;
• Un article de référence sur le décryptage d’Enigma : celui de Marian Rejewski, An Application of the Theory of Permutations in Breaking the Enigma Cipher, paru en 1980.

En français, on pourra lire :

• Enigma et la Seconde guerre mondiale, dossier réalisé dans le cadre d’un TPE par deux lycéens, Julien Milli et Guillaume Munch, qui détaille en particulier les fondements mathématiques du décryptage d’Enigma.
• Un dossier du site BibM@th : La cryptographie expliquée dont une partie concerne Enigma, son fonctionnement et son histoire ;
• Enigma : sur les traces de Turing, de Guillaume Poupard, plutôt destiné aux étudiants en informatique, qui détaille le fonctionnement d’Enigma et propose une méthode originale de cryptanalyse.

Vous pouvez lire aussi l’ouvrage de Simon Singh, « Histoire des codes secrets », Livre de Poche, 2001.