Une solution au problème de la génération de trajectoires
Au même instant, dans le laboratoire marseillais du professeur Bruno Poucet, un petit rongeur cherche son chemin, tandis qu’à l’hôpital Européen George Pompidou, le professeur Alain Carpentier, chirurgien cardiologue, et son équipe, s’apprêtent une nouvelle fois à sauver une vie. Dans les deux cas, le même type de calcul mathématique est en train de s’effectuer. Certes, pas tout à fait avec le même outil : approchons-nous pour regarder.
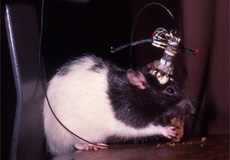
Dans le laboratoire de Marseille, c’est dans l’hippocampe du petit rongeur, cette partie du cerveau qui est située sous le cortex, que le calcul est en train de se dérouler. Le problème c’est que – oh oui – il y a un petit morceau de fromage aux effluves attirants, là, pas loin, mais fichtre, le chemin pour y parvenir est bigrement compliqué ! Cela dit, peu importe qui a pu faire une chose pareille, car dans l’hippocampe de notre petit animal quelque chose de fantastique est en train de se produire : chaque lieu, chaque endroit de ce labyrinthe à l’issue prometteuse est en train de se faire répertorier, en vrac d’ailleurs, mais au fur et à mesure des essais, voilà qu’un chemin, découpé en toutes petites portions, commence à émerger de ces neurones à l’activité de plus en plus structurée. Et soudain, ça y est, sans hésitation, la sortie est par là : ah ! le délicieux fromage est enfin trouvé.
 |
 |
|
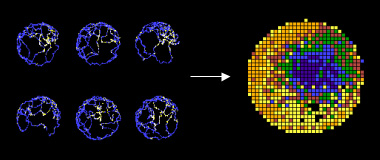
Au fur et à mesure de ses déplacements, la cellule de lieu de l’hippocampe observée par le biologiste décharge selon la position absolue de l’animal dans la scène : d’où son nom de « cellule de lieu ». On distingue pour six trajets marqués en bleu et blanc les portions où la cellule est inactive (en bleu) ou active (en blanc), toujours au même endroit. Si on cumule toutes ces données, dans la vue de droite, il apparaît une véritable cartographie où les zones qui correspondent à l’activité de cette cellule sont bien localisées. Images : Bruno Poucet. |
|
Ce que notre petit rongeur ignore, c’est que quelqu’un avait tout prévu : le labyrinthe, mais aussi ces petits fils indolores qui sortent de son cerveau et qui, reliés à un ordinateur, ont pu délivrer un maximum d’informations sur les calculs de trajectoire que l’hippocampe et les structures cérébrales connexes ont effectués. Mais pour l’instant, le professeur Poucet fait une pause. Peut-être pense-t-il à cette première médicale qui a été retransmise à la télé.
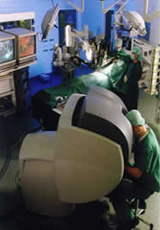
Le robot Da Vinci.
Au premier plan, le chirurgien et la console maître ; au second plan : le patient et la console esclave.
Marcelle (ou quel que se soit son prénom), les hippocampes de rats, je préfère vous le dire sans détour : c’est le cadet de ses soucis. À travers le rideau de larmes que cette jolie petite vieille dame essuie délicatement de son mouchoir brodé, elle ne pense qu’à une chose : que c’est trop tôt, beaucoup trop tôt, que son André ne peut pas partir comme ça, pas encore, même si ce crétin a eu bien tort de trop manger et de manger un peu trop arrosé. Ah ça il va l’entendre, celui là, quand il va se réveiller ! Oh oui. Oui. Pourvu que. Pourvu que son André puisse se réveiller.
Tout de même, je vous le demande un peu, à quel monde en est-on arrivé ? « Pas opérable », avait dit le premier chirurgien, c’était pourtant un « simple » pontage coronarien. Mais le reste du corps aussi était bien abimé. Alors, ouvrir la cage thoracique pour aller faire ce travail de couture, ça allait forcément mal se passer : « mort guéri », il paraît qu’on dit. Et puis, il y avait eu le Pr Carpentier, qui lui avait parlé d’un… robot !
Et maintenant, Marcelle essaie de s’imaginer les trois chirurgiens autour de l’énorme machine, qui a juste fait trois petits trous entre les côtes de son André, pour limiter le choc opératoire, et le Pr Carpentier qui pilote une caméra stéréoscopique en plongée entre poumons et cœur, et deux pinces, en train de coudre un nouveau vaisseau sanguin. Il y a même la télé qui filme ! D’ailleurs, il pourrait bien y avoir le Pape, tiens, pourvu qu’on le lui rende, son André.
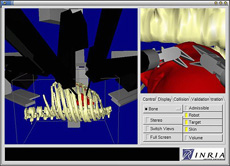
Planification de chirurgie assistée par ordinateur.
Image © Inria – Équipe CHIR.
Elle a tout de même demandé à cette informaticienne, Ève Coste-Manière, dont l’équipe a conçu et développé les mécanismes logiciels les plus complexes, comment le robot se débrouillait. Eh bien figurez-vous, un des problèmes serait de générer une trajectoire pour les nombreux degrés de liberté du robot chirurgical, à travers le labyrinthe que représente le fait d’arriver à recoudre ce qu’il faut à son André.
Ce qu’il ne faut pas entendre ! En attendant, elle passerait bien à la pâtisserie : un énorme Paris-Brest, c’est le gâteau préféré de son André. Ils pourraient le partager tout doucement, tous les deux, en cachette des infirmières. Il paraît qu’il vient juste de revenir à sa chambre et qu’il va bientôt se réveiller. Il aura sûrement faim, ce goinfre, elle le connaît.
La stratégie à laquelle Dédale n’avait pas pensé
Le robot chirurgical, comme le rongeur, au départ, est dans un état donné. Son état, ce sont tous les degrés de liberté qui vont lui permettre d’effectuer la trajectoire. Pour le rongeur, ce sont ses muscles. Pour le robot, entre son socle mobile, ses pinces, sa caméra stéréoscopique, il y a une vingtaine de degrés de liberté. Trouver une trajectoire qui permette de passer d’un état à un autre, cela veut dire trouver pour tous les degrés de liberté une courbe qui parte de l’état initial et qui aboutisse à l’état final souhaité. On représente donc toutes les variables du problème dans un espace dont les dimensions correspondent à chaque paramètre à ajuster : il s’agit donc d’un espace de grandes dimensions.
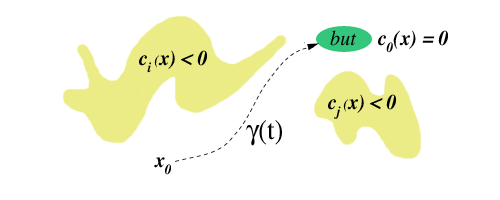
Représentation schématique du problème de la génération de trajectoire.
D’un point de départ x0, il faut atteindre un but défini par une région de l’espace. Ce but se formalise par une équation c0(x) = 0 qui doit être vérifiée pour y arriver. De même, chaque obstacle est une région de l’espace dont la frontière est définie par une équation ci(x) = 0 qui doit ne pas être vérifiée (sinon une collision se produirait). On cherche donc à maintenir ci(x) > 0 (qui correspond à l’extérieur de l’obstacle).
Pour passer d’un état initial x0 à un état final x00, le chemin le plus court… serait un segment de droite reliant ces deux points, s’il n’y avait ni obstacle, ni contrainte. Des obstacles physiques, certes, comme le mur du labyrinthe du rongeur de Bruno Poucet ou les côtes et les organes de celui que nous nous sommes permis d’appeler André. Mais il y a d’autres contraintes à respecter : ne pas aller trop vite pour éviter de déraper, par exemple, cela veut dire ne pas dépasser une certaine vitesse, donc mettre un obstacle dans l’espace des vitesses possibles. Mathématiquement, cela signifie respecter une certaine inégalité.
Ce qu’il faut bien comprendre ici, c’est que dire « je vais résoudre un problème de calcul de trajectoire » c’est se donner un défi aussi compliqué que « je vais concevoir un algorithme qui va être capable de faire passer n’importe quel système d’un état dans un autre » donc capable de réaliser une action robotique peut-être bien compliquée.
C’est là un des grands défis informatiques auxquels les chercheurs se sont attaqués.
La bonne nouvelle, c’est qu’il existe une « solution universelle » à ce problème compliqué. Deux chercheurs américains, Christopher Connolly et Roderic Grupen, l’ont mis à jour il y a quelques années.
Prenons le labyrinthe avant que notre petit rongeur ne s’y hasarde, et jetons un drap sur lui, en faisant bien attention qu’au but à atteindre le drap touche le sol. Sur les murs du labyrinthe, le drap est à la hauteur la plus élevée. Ailleurs, le drap est à une hauteur intermédiaire. Posons ensuite une bille extrêmement légère à l’endroit initial et… laissons-la rouler : si le drap est bien lisse, sans pli, alors la bille va tout naturellement rouler de son point initial au point le plus bas : le but à atteindre. Elle ne rencontrera jamais d’obstacle, puisqu’elle roule vers le bas, le drap étant lui en hauteur sur le bord des murs du labyrinthe. Nous venons de construire un dispositif qui génère automatiquement une trajectoire de n’importe quel point initial vers le but choisi.
Il est très important que le drap n’ait pas de pli, ni de cuvette intermédiaire où la bille resterait coincée sans aller jusqu’au but recherché, mais ça aussi, il est possible de s’en assurer.
Une méthode à fort potentiel
Mathématiquement, définir un tel drap revient à définir pour chaque point de l’espace une valeur de hauteur : on parle de potentiel. Ce potentiel a une valeur minimale au but à atteindre, maximale au niveau des obstacles. Faire rouler la bille veut simplement dire se déplacer de proche en proche dans une direction où le potentiel est plus petit, pour aller vers son minimum. Avoir un drap sans pli veut dire avoir un potentiel sans minimum local, où partout il y a une pente : la variation de hauteur ne doit jamais s’annuler, sauf au but.
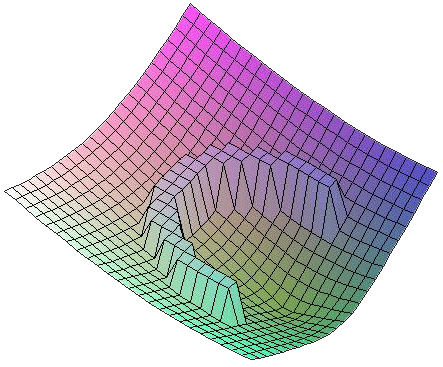
Un exemple de potentiel, avec un obstacle en fer à cheval et un but à atteindre au centre du carré. Le potentiel décroît régulièrement en direction du but et croît en direction des obstacles : suivre localement la pente de ce critère permet d’atteindre automatiquement le but en contournant les obstacles.
Les mathématiciens savent depuis des années que certains potentiels, appelés potentiels harmoniques parce qu’ils sont définis par une fonction harmonique, vérifient exactement cette propriété. En effet, une fonction harmonique est caractérisée par le fait que chaque valeur correspond à la valeur moyenne des valeurs voisines, par conséquent elle n’a pas d’« aspérités », de minima locaux.
Mais cette solution présente un avantage supplémentaire : les potentiels harmoniques peuvent facilement s’additionner entre eux. Alors, il devient possible non seulement de générer en une fois une trajectoire dans un espace entièrement connu à l’avance, mais aussi, au fur et à mesure de l’exploration, de définir des petits bouts de potentiel en vrac : des parties qui correspondent à une répulsion par rapport aux obstacles au fur et à mesure de leur découverte, et bien sûr un morceau qui correspond à une attirance vers le but. La somme de tous ces morceaux forme automatiquement le potentiel dont on a besoin. Toute ressemblance avec les cellules de l’hippocampe qui s’activent au fur et à mesure du passage d’une partie d’un lieu à un autre ne serait pas fortuite : cette ressemblance a même été détaillée par les chercheurs qui modélisent cette faculté au niveau biologique et artificiel.
Nous allons très précisément définir le potentiel harmonique à utiliser, puis expliquer comment l’utiliser.
Au début, seul le but à atteindre est pris en compte. Si le cerveau du rat ou le robot veulent atteindre un point B, leur but, le potentiel se calculera ainsi :
V+(P – B) = -1 / distance (P, B)n-2
où P désigne la position du rat ou du robot et où n > 2 est le nombre de degrés de liberté du système moteur du rat ou du robot (ce nombre est élevé, puisque pour le robot par exemple, il s’agit de toutes ses articulations). Minimiser ce potentiel conduit bien à rapprocher P de B, donc à se rapprocher du but, cela va créer une force d’attraction. Mieux, ce potentiel est harmonique, car il n’a pas de minima locaux. C’est d’ailleurs le plus simple des potentiels harmoniques.
Ensuite, à un instant donné, le cerveau du rat ou notre robot reconnaissent des obstacles qu’ils vont éviter ou des contraintes qu’ils ne veulent pas enfreindre, des obstacles virtuels en quelque sorte. À chaque instant t, ils vont donc considérer le point Ot le plus proche d’eux sur cet obstacle ou cette contrainte, et utiliser le bout de potentiel harmonique :
V–(P – Ot) = +1 / distance (P, Ot )n-2
Et là, l’effet inverse se produit : minimiser cette partie du potentiel éloigne P du point Ot choisi sur l’obstacle, une force de répulsion est créée.
Comme les potentiels s’ajoutent, le potentiel complet sera :
V(P) = V+(P – B) + V–(P – O1) + V+(P – B) + V–(P – O2) + … + V+(P – B) + V–(P – Ot) + …
c’est à dire tout simplement la somme des attractions du but et des répulsions des obstacles. Ce potentiel est harmonique, car c’est la somme de fonctions harmoniques.
Ici, le potentiel a donc une taille qui croît linéairement avec le temps : c’est beaucoup mieux que d’autres méthodes qui ont des potentiels dont la taille explose (croît exponentiellement) avec le nombre de degrés de liberté et la taille de l’espace.
Autre avantage, c’est au fur et à mesure de son exploration que le cerveau du rat ou le robot construisent ce potentiel. Ils sont donc adaptatifs, ils peuvent aussi tenir compte du fait que le but peut changer, qu’il y a des sous-buts à atteindre avant d’atteindre le but, que l’on peut explorer sans but (dans ce cas, on ne prend en compte que la répulsion des obstacles), puis découvrir un but et s’en approcher, etc. La méthode est flexible.
Ce qui a été démontré (ce n’est pas complètement évident, mais pas si difficile !), c’est que minimiser V(P) nous conduit forcément au but, en évitant toujours les obstacles.
Comment utiliser ce potentiel harmonique ?
Pour passer d’un point P à un point voisin, on calcule le gradient du potentiel, c’est-à-dire sa variation pour chaque degré de liberté. Il y a même des formules : le gradient de V+(P – B) est gradV+(P – B) = (P – B) / distance (P, B)n et le gradient de V–(P – Ot) est gradV–(P – Ot) = – (P – Ot) / distance (P, Ot)n. Combiner ces formules en les ajoutant permet de calculer gradV(P), c’est-à-dire la direction dans laquelle il faut bouger pour minimiser un tout petit peu V(P). On avance en effet de manière « infinitésimale », c’est-à-dire pas à pas, à tout petits pas.
Et… c’est tout ! Il n’y a rien de plus à calculer, exactement comme dans le petit cerveau du rat, qui effectue sûrement des opérations sans « raisonnement » de haut niveau, et pourtant va explorer toute votre maison, voler votre fromage et accéder à une cachette bien inaccessible… tandis que votre cerveau humain sera bien embarrassé !
Testez la méthode sur une applet
On peut donc définir un calcul qui, en se basant sur un tel potentiel, va générer une trajectoire « automatiquement ». Nous vous proposons ici un petit exemple où vous pouvez regarder se tracer une telle trajectoire générée par un mécanisme qui a été défini à partir d’un calcul biologiquement plausible, peut-être voisin de ce qui se fait dans les structures cérébrales qui ont cette faculté.
Ce petit exemple est juste une illustration, mais le même calcul a été utilisé pour résoudre des problèmes plus compliqués.
Vous devriez aussi chercher à… faire échouer le mécanisme ! En effet, on ne trouve pas toujours de trajectoire d’un point donné à un autre. C’est peut-être trop long (le présent calcul s’arrête de lui-même au bout de quelques centaines de pas de calcul), ou bien la solution passe peut-être trop près des obstacles… quel que soit le fromage, un rongeur peut se décourager !
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Cliquez sur Génération de la trajectoire pour visualiser le tracé. Nous vous proposons deux exemples : simple, avec un obstacle triangulaire, et labyrinthe.
Vous pouvez modifier le point de départ avec le bouton de droite de la souris ou en combinant clic gauche et touche contrôle, et le point d’arrivée avec le bouton du milieu ou en combinant clic gauche et touche majuscule. En cliquant sur Effacer, vous effacez l’interface avec les points et les obstacles, vous pouvez alors placer d’autres points (comme indiqué précédemment) et tracer vous-même des obstacles avec le bouton de gauche de la souris (cliquez deux fois pour finir un tracé).
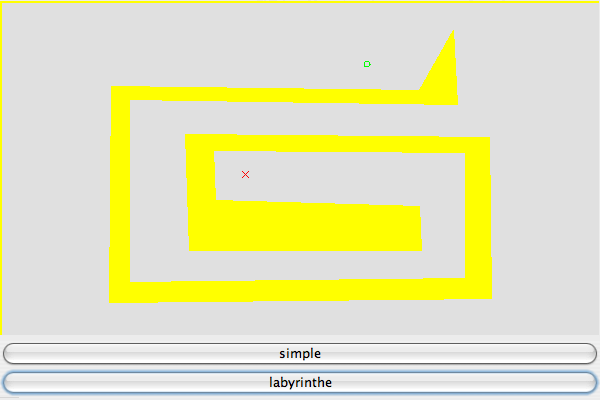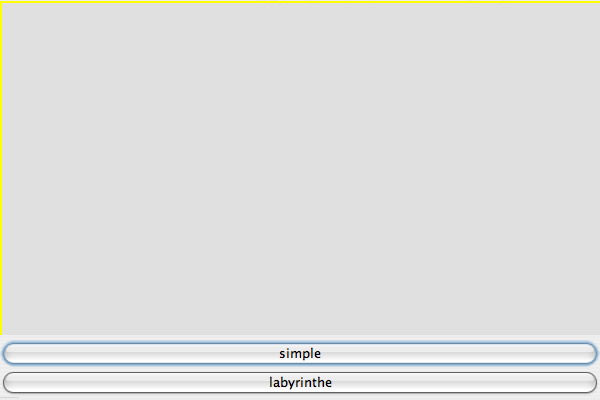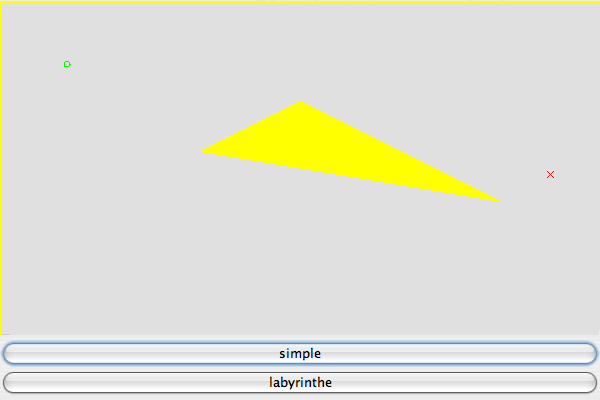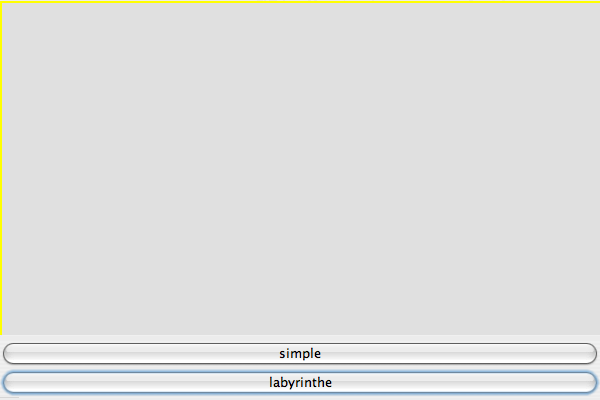
Deux exemples de génération de trajectoire, le premier avec un obstacle labyrinthe, le deuxième avec un obstacle triangulaire simple.
Des solutions alternatives
D’autres solutions existent pour résoudre ce problème de génération de trajectoire. Dans le cas de la chirurgie cardiaque, c’est une méthode géométrique qui a été employée. Les obstacles ont été triangulés et au sein de cette représentation, la trajectoire n’est plus à rechercher que sur le diagramme des médiatrices. Le problème a ainsi été suffisamment simplifié pour recevoir une solution voisine de celle décrite ci-dessus, mais avec une meilleure efficacité.
Dans d’autres cas, il ne s’agit pas de trouver une trajectoire compliquée, mais de suivre ou de corriger une trajectoire prédéfinie : la modélisation du problème est alors plus simple.
Dans tous les cas, résoudre ce problème représente un pas important tant pour la recherche en informatique que pour de nombreuses applications.
Plusieurs domaines des mathématiques se sont attaqués à ce grand problème de la génération de trajectoire. À vrai dire, ils s’y sont presque tous mis !
Les analystes, ceux qui résolvent des équations différentielles comme notre méthode de potentiel, ont proposé des solutions voisines de celle décrite ici. Mais souvent bien plus compliquées, car ils cherchent non seulement à résoudre le problème de la trajectoire, mais aussi à commander le robot ou le véhicule correctement sur cette trajectoire…
Les géomètres, ceux qui modélisent les formes, ont proposé des solutions où l’espace était triangulé, c’est-à-dire décomposé en petits éléments géométriques, en maillages. Des méthodes issues de ces idées sont utilisées en chirurgie assistée par ordinateur.
Les informaticiens, ceux qui font des recherches en intelligence artificielle, ont proposé des méthodes algorithmiques inspirées de la nature, où le problème est résolu par des agents qui calculent la solution de manière coopérative.
Les algébristes, ceux qui résolvent des équations faisant intervenir des polynômes, ont eux aussi attaqué le problème d’une tout autre façon : ils ont défini chaque but et chaque obstacle par une équation (ici une équation polynomiale) et profité de ce cadre pour proposer des solutions très puissantes, souvent connues comme solutions au « problème du déménageur de piano » – sortir un meuble, piano ou armoire d’une pièce sans le cogner aux murs du couloir ou de l’escalier, vous avez sûrement connu ça ! – un vrai problème de génération de trajectoire, où ladite trajectoire est aussi compliquée que celle qui permet de faire un créneau avec sa voiture ou de piloter un bras de robot…
Et la liste n’est pas épuisée ! Si la méthode détaillée ici est la plus proche de ce qui se passe dans un cerveau biologique, les autres sont peut-être mieux adaptées à certains calculs, selon le type de robot. En tout cas, tous ces mathématiciens l’ont bien illustré… même si eux aussi continuent comme vous à se demander comment le petit rat du grenier a encore réussi à manger le gruyère de la réserve, sans jamais rester coincé dans le dédale des plafonds et des planchers…
Marcelle et André sont des personnages imaginaires, évidemment, mais le robot qui aide le Pr Carpentier à sauver des vies existe, et moi, je peux vous le certifier : le regard d’une « Marcelle » qui retrouvait « son André », ce regard, mes collègues et moi l’avons croisé. Pour de vrai.
Et le petit rongeur, je l’ai vu lui aussi, quand j’ai rendu visite à mes collègues du laboratoire de Marseille. En partant, en revanche, ça a été vraiment la galère, je vous dis pas le labyrinthe pour sortir de Marseille. J’en ronge encore ce qu’il reste de frein à ma pauvre voiture. Comment ? Utiliser mon calcul de génération de trajectoire ? Non mais, je vous parle de Marseille, là, eh ? Les mathématiques c’est bien joli, mais il y tout de même des problèmes où il vaut mieux s’en remettre à la Bonne Mère, peuchère : informaticien mais pas fada, vé !
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
