Mieux prévoir les phénomènes météorologiques

Environnement & Planète

Modélisation & Simulation

Optimisation Prévision

Lorsqu'on se remémore l'ouragan Katrina, travailler à améliorer les prévisions météorologiques prend tout son sens. Pour cela, il faut être capable de prendre en compte des sources d'information hétérogènes, et de coupler des modèles différents.

En cas d’ouragan ou d’inondation, la prévision météorologique peut contribuer à sauver des vies humaines lors d’événements paroxysmiques comme Katrina, mais aussi éviter des évacuations coûteuses lorsqu’elles s’avèrent inutiles. Cependant, son intérêt ne se limite pas à ce domaine. Du point de vue économique, elle apporte une aide à la gestion des centrales électriques et des barrages. Elle permet aussi d’optimiser les trajectoires d’avions pour profiter des courants jet en haute altitude. La prévision océanique est utile pour définir les trajectoires de navires ou les zones de pêche. Pour la Défense, elle conditionne le positionnement des sous-marins.

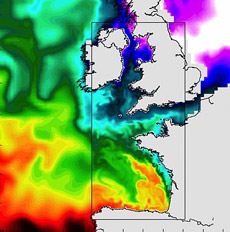
Simulation numérique de la circulation océanique : visualisation à haute résolution du champ de température de surface pour le golfe de Gascogne et le plateau celtique (la zone à haute résolution est encadrée, seule une partie du domaine à basse résolution, qui en fait couvre tout l’océan Atlantique Nord, est affichée). Image : Projet IDOPT.

La prévision est complexe, car elle fait intervenir de nombreux facteurs. Si l’on considère le cas des ouragans, ceux-ci ne peuvent se déclencher que pendant une saison qui court de septembre à novembre, période où la température de l’eau est la plus chaude. Les ouragans sont nourris par les flux de vapeur d’eau produits par les eaux océaniques chaudes. La genèse et le développement des ouragans dépendent donc de l’état de l’atmosphère, de l’océan et de leurs interactions.

En vue de la prévision, on dispose de plusieurs sources d’information hétérogènes tant en nature qu’en qualité et densité : de l’information de type mathématique, physique, statistique, ainsi que des images.

L’information de type mathématique, ce sont les équations qui gouvernent l’évolution des fluides : océan et atmosphère. Il s’agit de systèmes d’équations complexes que l’on sait résoudre de façon approchée sur des ordinateurs de grande puissance. L’information de type physique est obtenue par des mesures directes ou à distance, effectuées par exemple par des satellites. L’information de type statistique porte sur les événements passés. Enfin, on dispose d’images comme celles fournies par les satellites Météosat (dont on voit les produits à la télévision dans les bulletins quotidiens de prévision météo).

Pour prévoir, il faut savoir d’où l’on part

Dans notre cas, il faut reconstituer l’état de l’atmosphère et de l’océan à un instant donné, puis l’on obtiendra la prévision en résolvant les équations. Mais ceci est vrai pour tout domaine : si l’on veut prévoir, il faut d’abord savoir d’où l’on part. Pour déterminer cet état initial, le problème clé est le couplage des sources d’information.

Dans les années quatre-vingts, François-Xavier Le Dimet a pour cela proposé d’utiliser des techniques de contrôle optimal pour reconstituer l’état de l’écoulement (dans notre exemple, celui de l’atmosphère et de l’océan). En France, ces techniques ont été développées au sein de l’INRIA sous l’impulsion de Jacques-Louis Lions. Le principal inconvénient de cette approche était de multiplier le coût de calcul par un facteur 10. Mais c’était le prix à payer pour améliorer la prévision, et cette méthode est maintenant utilisée de façon opérationnelle par de nombreux centres météorologiques (Météo France, Centre européen de prévision à moyen terme ECMWF situé à Reading en Grande Bretagne…) et a également été adoptée en 2005 par le Japon.

L’exemple le plus simple qui me vient à l’esprit est un peu belliqueux. Supposez qu’ayant un canon et un obus, vous vouliez faire un don, pas tout à fait gracieux, de l’obus à votre ennemi préféré. Les caractéristiques de l’obus dépendent du seul fabricant, la plus importante étant sa vitesse initiale. Si vous tirez depuis votre territoire, un point fixé, les deux degrés de liberté dont vous disposez sont l’élévation et l’azimut du canon. Ce sont les variables de contrôle.

Mathématiquement, votre problème est de choisir ces variables de telle sorte que le projectile arrive aussi près que possible de la tanière de votre ennemi, tout en sachant que la trajectoire de l’obus vérifie les lois de la pesanteur et de la résistance de l’air.

Pour résumer on a donc :

deux variables de contrôle : l’élévation et l’azimut du canon au moment de la mise à feu ;
une équation d’état représentant la trajectoire de l’obus : c’est un système d’équations différentielles dont les variables sont les coordonnées de l’obus en fonction du temps x(t), y(t), z(t) : rien d’autre que la loi de la gravité (dura lex, sed lex !) et la résistance de l’air à l’avancement du projectile ;
une fonction – dite fonction coût – qui mesure la différence entre le but fixé et la position du projectile au moment de l’impact.

Le problème que vous vous posez ( si vous êtes méchant !) est : comment déterminer les variables de contrôle, c’est-à-dire comment positionner votre canon au départ, de manière à minimiser la fonction coût, c’est-à-dire arriver aussi près que possible de la cible ? C’est là un problème d’optimisation que vous devez résoudre.

La situation en météorologie n’est pas conceptuellement différente : comment choisir au mieux l’état initial de l’atmosphère (le contrôle), de façon à ajuster au mieux les observations (la fonction coût), tout en sachant que l’atmosphère vérifie les équations de la dynamique des fluides.

La principale différence réside dans la gestion du calcul : on passe de deux variables de contrôle (les angles du canon) à plusieurs millions (le vent, la température, l’humidité, la pression aux nœuds d’un maillage tri-dimensionnel couvrant toute l’atmosphère terrestre à l’instant initial de la période d’observation).

Du point de vue mathématique, on a un problème d’optimisation, dont on va déterminer une solution approchée par une méthode itérative nécessitant l’évaluation de la dérivée (le gradient) de la fonction coût par rapport aux variables de contrôle. Ce calcul de gradient sur des fonctions définies par des codes informatiques très complexes fait l’objet de recherches et de développements (logiciel TAPENADE) dans le cadre du projet TROPICS de l’INRIA Sophia Antipolis.

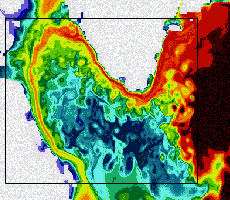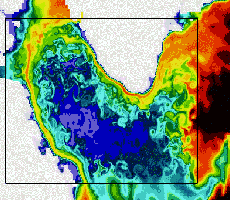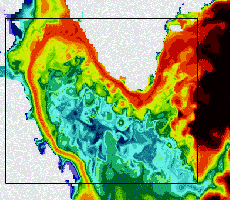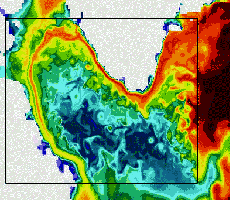
Simulation numérique de la circulation océanique : visualisation à haute résolution du champ de température de surface de la mer du Labrador. Image : Projet IDOPT.

Les chercheurs de l’équipe IDOPT, dont François-Xavier Le Dimet a été responsable pendant 12 ans, puis de l’équipe MOISE, dirigée par Éric Blayo, qui en a récemment pris la suite, mènent des recherches qui permettent d’améliorer ces méthodes. Ils s’intéressent à la modélisation des fluides géophysiques : océan, atmosphère, eaux continentales de surface et souterraines.

La mise au point de ces modèles est complexe, et nécessite une collaboration importante avec les océanographes, les hydrologues et les météorologues. Elle nécessite des développements mathématiques tant sur l’étude des équations et de leurs approximations que sur la conception de méthodes performantes pour les résoudre.

En effet, toutes les composantes de l’environnement communiquent. Ainsi, l’atmosphère agit sur l’océan et sur les rivières, et la réciproque est vraie. Le développement de la puissance de calcul disponible va permettre de coupler les modèles afin d’aller vers une prévision plus précise.

Un modèle océanique, tel que celui utilisé par le projet Mercator Océan, est construit à partir des équations qui traduisent l’évolution temporelle de la vitesse, de la température et de la salinité de l’océan dans ses trois dimensions horizontales et verticale. Ces équations utilisent des approximations de la sphéricité de la Terre, de la profondeur de l’océan, faible par rapport au rayon de la Terre, de la répartition hydrostatique des pressions sur la verticale, des variations de densité, négligeables sauf pour la flottabilité, de l’incompressibilité, et de la force de Coriolis, due à la rotation de la Terre.

Une équation d’état, non linéaire, couple par ailleurs les deux traceurs actifs (température et salinité) à la densité et au champ de pression.

La formulation repose ainsi sur six équations traduisant l’équilibre du moment, l’équilibre hydrostatique, l’incompressibilité, la conservation de la chaleur et du sel, et une équation d’état, ces équations liant les variables du problème, fonctions de l’espace et du temps : la vitesse, la pression, la densité in situ, la température potentielle et la salinité.

Modèles et données associées

Mais l’utilisation de modèles ne prend tout son sens que si on a les données associées. Obtenir ces données n’est pas toujours aisé. Le coût d’une mesure directe est élevé voire prohibitif, par exemple pour mesurer l’humidité du sous-sol. L’observation de la Terre par des satellites fournit une gigantesque quantité d’information, dont la plupart n’est pas utilisable directement.

En revanche, lorsque de nouvelles données précises sont disponibles, cela peut entraîner des progrès considérables dans le domaine concerné. Ainsi récemment, les satellites TOPEX-Poséidon et Jason, par une mesure très précise de la hauteur de la surface de l’océan, ont initié une véritable révolution en océanographie, concrétisée aujourd’hui dans le projet Mercator Océan, qui délivre des analyses et des prévisions océanographiques en temps réel. L’équipe IDOPT, notamment par les travaux d’Éric Blayo et Laurent Debreu sur l’amélioration des modèles, a été au centre des développements méthodologiques pour ce projet.

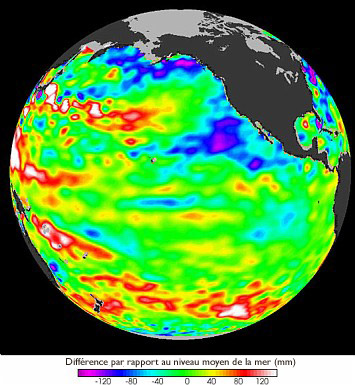
Altimétrie de la surface de l’océan Pacifique, mettant en évidence El Niño. Image : Projet IDOPT.

Autre recherche en cours, l’assimilation des images provenant des satellites. Les images de l’évolution de l’environnement fournies par les satellites sont utilisées à l’heure actuelle principalement de façon qualitative. Dans le projet ASSIMAGE financé par l’ANR et piloté par IDOPT puis MOISE, on se propose d’assimiler ces images, en utilisant toujours des techniques de contrôle optimal dans des modèles en vue d’améliorer la prévision. Pour cela, une ouverture vers les spécialistes de traitement d’images a été nécessaire.

Les images que l’on voit de la Terre dans les bulletins de prévision météorologiques sont très parlantes : on voit le déplacement des fronts et des masses nuageuses, souvent on peut avoir une première approximation du temps qu’il va faire en extrapolant les trajectoires des masses d’air ou des contours des images infrarouges donnant les températures.

Or à l’heure actuelle, on ne sait pas intégrer de façon systématique cette information dans des modèles de prévision. C’est le but de cette recherche sur l’assimilation d’images : comment coupler de l’information apportée par des images et leur dynamique avec de l’information mathématique donnée par des modèles.

C’est là un problème très générique, que l’on trouve dans d’autres domaines comme la médecine, où l’on peut par exemple observer la dynamique de l’évolution du cœur.

La collaboration entre disciplines différentes est une tâche longue et difficile, mais ô combien exaltante ! Coupler des modèles, c’est aussi coupler des disciplines qui ont des langages, des pratiques différentes. Les mathématiques servent ici comme socle commun de connaissances, et il revient au mathématicien de jouer un rôle fédérateur dans les sciences de l’environnement.

Newsletter

Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité