
L’évolution des galaxies
Les galaxies comme la Voie lactée regroupent des étoiles par centaines de milliards. Comment se sont-elles formées ? Comment évoluent-elles ? Pour le déterminer, il faudrait expérimenter : manipuler les galaxies en laboratoire à la manière d’un démiurge chimiste ; franchir d’un même regard des milliers d’années-lumière ; saisir des évolutions ou des interactions entre étoiles sur des millions voire même des centaines de millions d’années, jusqu’à plusieurs milliards d’années… Irréalisable ? Grâce aux simulations numériques, les astronomes ont été les témoins de phénomènes dynamiques, que les calculs analytiques ne pouvaient traiter, ni même soupçonner.

La plupart des galaxies spirales, ici NGC 1097 située à 45 millions d’années-lumière, ont une structure rectangulaire centrale, une « barre d’étoiles ». Les barres et les bras des galaxies spirales sont des régions denses en étoiles, en poussières et en gaz. La prise en compte de tous ces composants dans les simulations nous aide à comprendre leur formation.
Photo © NASA, European Space Agency, Steven Beckwith Space Telescope Science Institute and Hubble Heritage Team
Soucieux de comprendre la forme spirale des galaxies, les astronomes ont commencé à modéliser des ensembles d’étoiles dans le courant des années 1960. Pour mener à bien les calculs sur des machines limitées en mémoire, ils étaient obligés d’utiliser une approximation drastique : ils supposaient que les bras spiraux s’enroulaient sur eux-mêmes, d’une manière compacte. Dans ce cas, la perturbation gravitationnelle due aux bras spiraux lointains devenait négligeable, et le calcul se limitait ainsi aux perturbations locales.
Nombre astronomique et résolution spatiale
Comment calculer les interactions de cette myriade d’étoiles ? Les capacités des ordinateurs ne permettent pas de traiter les centaines de milliards d’étoiles d’une galaxie. Une première approximation consiste à réduire le nombre d’étoiles du modèle, à un million par exemple : chaque « pseudo-étoile », appelée particule, représente de l’ordre de 100 000 étoiles. Cette approximation a pour effet de limiter la résolution spatiale et en masse de la simulation : seuls les phénomènes à grande échelle sont représentés, comme si on les observait de loin. Cette approche statistique, au nombre de particules si éloigné du nombre réel, est-elle valable ? On peut en douter dans la mesure où certains comportements dépendent précisément de ce nombre, mais nous allons voir qu’une astuce nous autorise à le faire.
Dans ces modèles informatiques, on considère les étoiles comme des points sans collision ni rencontre : non seulement une collision directe entre deux étoiles est improbable, mais encore les rencontres gravitationnelles, au cours desquelles les trajectoires seraient modifiées, sont aussi négligeables. Chaque étoile n’est sensible qu’au champ gravitationnel moyen de l’ensemble des étoiles de la galaxie, et aucune n’est sensible à la présence de ses proches voisines. Cet effet, dit de champ moyen, est justement dû à la taille du système : le champ gravitationnel est lissé par le très grand nombre d’étoiles. La réduction du nombre d’étoiles simulées ne risque-t-elle pas d’introduire une granularité dans le champ ? Ne permet-elle pas la modification des trajectoires par collision entre particules voisines ?
La résolution spatiale trop grossière — c’est-à-dire lorsqu’on remplace 100 000 étoiles par une seule particule pour économiser le temps de calcul — introduit une grande granularité dans la physique du problème simulé, par rapport au problème réel à traiter puisque ce dernier a lui aussi une certaine granularité. En effet, les étoiles ne sont pas un gaz lisse et homogène : elles ressemblent plutôt à des points massifs (comme des « grains ») et discrets. Du grand nombre d’étoiles (100 milliards) résulte un potentiel gravitationnel très lisse, d’où la granularité est absente. Si le potentiel en 1/R était conservé pour les simulations, le potentiel résultant du nombre de particules simulé ne serait pas assez lisse, mais trop granuleux. C’est la raison pour laquelle on utilise un potentiel adouci.
Pour éviter cette granularité artificielle à petite échelle et la perturbation des orbites des étoiles, le champ gravitationnel est « adouci » par une loi simple. On remplace par exemple les forces de Newton en 1/R2 par des forces en 1/(R2 + a2), où R est la distance séparant deux particules à partir de leurs centres de gravité et a le paramètre d’adoucissement. L’effet de ce paramètre est de limiter les forces d’attraction à courte distance, et d’empêcher les interactions brutales entre particules proches. Ainsi, on retrouve le comportement « sans collision » des étoiles, mais en contrepartie, les simulations manquent de réalisme aux échelles de l’ordre de a. On voit ici comment le nombre de particules est relié à la résolution spatiale des simulations.
La forme des galaxies
Les galaxies spirales tournent sur elles-mêmes, un peu comme des frisbees, à la différence que les étoiles les constituant ne se déplacent pas toutes à la même vitesse. Il s’ensuit des différences de densité de la matière, qui se propagent dans tout le disque : ces ondes de densité sont responsables de l’apparition des bras spiraux. Cependant, on pouvait s’interroger sur le pouvoir prédictif des modèles évoqués ici, car la plupart des galaxies spirales ont des bras très ouverts, et non enroulés tels qu’on les supposait.
Dans les années 1970, les simulations numériques ont pris en compte l’autogravité des disques d’étoiles, traitant le problème à N corps gravitationnel, sans négliger la perturbation gravitationnelle due aux bras spiraux lointains. Il fallait toutefois faire une autre approximation. Quand N particules interagissent dans un champ de gravité, chaque particule interagit avec les (N – 1) autres, ce qui représente de l’ordre de N2 calculs directs : ce nombre devient ingérable quand N est grand. La plupart des simulations emploient des algorithmes, où le nombre de calculs est proportionnel à N log N au lieu de N2. L’un d’eux calcule le champ moyen sur une grille à trois dimensions. Les particules interagissent avec la grille, dont la maille détermine la résolution spatiale de la simulation. Cet algorithme est bien adapté à l’évolution des galaxies, car celles-ci sont assez homogènes en densité. Un autre algorithme est le « code en arbre ». Il distribue les particules (ou « feuilles ») en une structure hiérarchique ressemblant à un arbre : deux feuilles de cet arbre n’ont pas la même interaction selon qu’elles se trouvent sur une même « branche » ou sur des branches éloignées.
Réduire le temps de calcul pour une simulation prenant en compte un très grand nombre N de particules, qui interagissent entre elles, tel est le principe du code en arbre. Afin de minimiser le temps de calcul, on ne traite précisément que les interactions entre les plus proches voisins, et on ne fait qu’une approximation pour les particules lointaines. Ce code en arbre a des avantages non négligeables : là où le calcul exact prendrait un temps croissant équivalent à N2, le code en arbre ne prend qu’un temps de calcul croissant comme N log N.
L’arbre permet en outre de sélectionner les plus proches voisins. Le volume cubique contenant toutes les particules (la racine) est divisé en 8 cellules, par division d’un facteur 2 de la taille de la cellule, et ainsi de suite. À chaque itération, on s’assure qu’il existe des particules dans chaque cellule (ou chaque branche de l’arbre), avant de continuer une autre itération, jusqu’à ce qu’il n’y ait plus qu’une particule par cellule (le niveau des feuilles est atteint).
L’interaction gravitationnelle est prise en compte dans un petit voisinage de chaque point. Si une branche, ou cellule, est vue d’une particule donnée sous un angle assez petit, la branche n’est pas individualisée en feuilles, mais la particule va interagir avec toute la branche, comme s’il s’agissait d’une particule unique plus massive, et avec les développements multipolaires correspondant à la distribution de la masse sur la branche. Les interactions lointaines sont donc simplifiées.
Par ailleurs, le principe du code en arbre peut s’appliquer à d’autres problèmes d’interaction entre particules, qui privilégient l’interaction entre plus proches voisins, notamment à la recherche des voisins pour appliquer les forces de pression dans le traitement hydrodynamique d’un gaz ou les phénomènes électro-magnétiques.
 |
 |
|
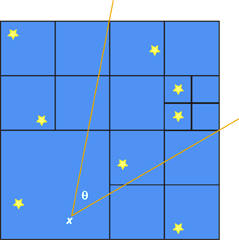
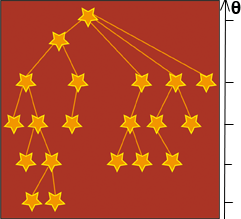
Ci-dessus, un algorithme du code en arbre, où les particules sont considérées de façon hiérarchique selon leur situation dans l’espace. Pour calculer l’interaction d’une étoile donnée en x (à gauche) avec toutes les autres, on trie d’abord les étoiles voisines selon leur distance. On regroupe les étoiles lointaines en « particules » plus massives, afin de diminuer le nombre d’interactions à calculer. La particule en x interagit de façon individuelle uniquement avec ses proches. Les groupes (ou boîtes) qui sont vus sous un angle ? petit (inférieur à une valeur critique) sont remplacés par une particule placée au centre de gravité de l’ensemble, et dont la masse est la somme des masses des particules. On représente cette hiérarchie de proximité sous la forme d’un arbre, où chaque niveau de branches correspond à une valeur de ? (à droite). Les particules proches dans une même branche interagissent individuellement (par la loi de Newton adoucie) ; l’attraction des particules éloignées est traitée de façon approchée par des groupes de particules plus massifs. |
|
Le code en arbre est adapté aux cas où la densité, et donc le type d’interaction entre les particules, varie d’une région à l’autre. Ces simulations à autogravité firent apparaître, à la surprise générale, des instabilités sous la forme de barres en travers des disques galactiques. On sait aujourd’hui, grâce aux images en proche infrarouge (à quelques microns de longueur d’onde) qui révèlent les vieilles étoiles, que la majorité des galaxies spirales, jusqu’à 80 pour cent, sont barrées. Mais avant de faire ces observations, le premier souci des modélisateurs fut de faire disparaître de leurs calculs cette barre indésirable, d’autant qu’elle est robuste et a une durée de vie supérieure à l’âge de l’univers. Il fallait donc expliquer que certaines galaxies ne sont pas barrées !
L’effet du gaz interstellaire
L’apparition d’une barre robuste au sein des galaxies spirales tenait au fait que ces simulations ne faisaient intervenir que les étoiles, qui sont un composant sans collision des disques galactiques, sans inclure le gaz interstellaire. Aujourd’hui, les simulations numériques prennent aussi en compte le gaz, ainsi que la formation d’étoiles à partir du gaz et les phénomènes d’autorégulation concomitants. Le gaz ne constitue qu’un dixième environ de la masse d’une galaxie : c’est la raison pour laquelle on l’avait négligé. Il a néanmoins un rôle important dans la dynamique galactique du fait qu’il est très dissipatif.
La majeure partie de la masse du gaz est distribuée sous forme de nuages interstellaires, qui se conduisent comme des particules balistiques. Contrairement aux étoiles, qui ne se rencontrent qu’exceptionnellement, les nuages interstellaires entrent de temps en temps en collisions inélastiques, où une grande partie de l’énergie relative est dissipée sous forme de rayonnement. On représente alors les nuages interstellaires sous la forme de particules collantes, qui subissent des collisions de façon intermittente. Une autre partie du gaz est diffuse et se comporte comme un fluide, soumis à des forces de pression, à des ondes de choc, à des chauffages et à des refroidissements. Pour décrire cette situation, un algorithme du code en arbre, appelé SPH (Smoothed Particule Hydrodynamics), considère des particules de taille variable, plus petites dans les zones denses. On calcule chaque grandeur comme la densité, la pression, en la sommant sur les plus proches voisins d’une particule donnée. D’autre part, une série d’algorithmes dits AMR (Adaptive Mesh Refinement), utilisent des résolutions spatiales qui s’adaptent aux zones denses, par des zooms successifs.
Le traitement complet de tous les composants d’une galaxie a permis de mieux comprendre les différentes étapes de son évolution. On a pu observer qu’un disque uniquement composé d’étoiles forme spontanément une spirale transitoire qui se transforme en barre, subsistant jusqu’à la fin des simulations. Des instabilités chauffent le disque d’étoiles et rendent instables les spirales. Ainsi une galaxie lenticulaire, qui a perdu son gaz depuis longtemps, reste barrée, mais ne présente pas de bras spiraux. En revanche, le gaz interstellaire dissipe la chaleur due aux instabilités, et la galaxie conserve sa morphologie spirale.
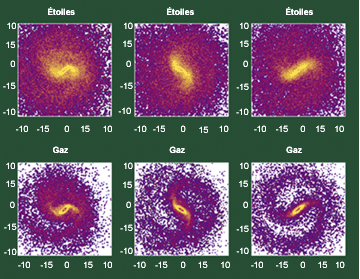
Trois époques d’une simulation de galaxie isolée, où se développent une barre et des bras spiraux, et où l’on a séparé les étoiles (en haut) du gaz (en bas). Les étoiles seules forment une galaxie lenticulaire barrée, sans bras spiraux. Le gaz interstellaire se refroidit sans cesse, dissipant par rayonnement l’énergie cinétique relative entre particules. Il est ainsi plus instable vis-à-vis des perturbations gravitationnelles, et maintient la structure spirale.
Images : Françoise Combes
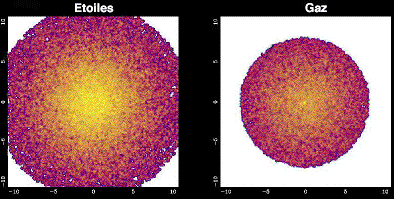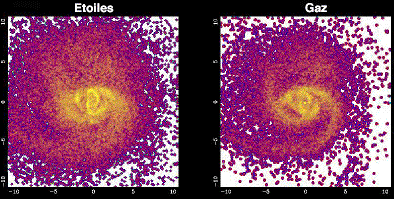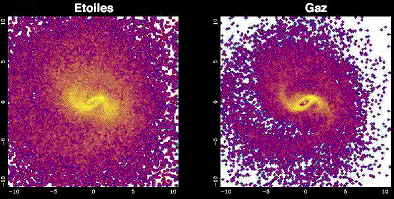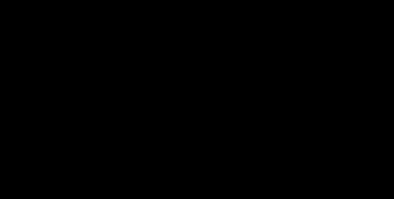
125 époques d’une simulation de galaxie spirale, les étoiles (à gauche) ayant été séparées du gaz (à droite).
Images : Françoise Combes
Par ailleurs, cette dissipation de l’énergie entraîne la chute du gaz vers le centre de la galaxie, où il forme de nouvelles étoiles, ce qui affaiblit ou détruit la barre. Ce phénomène d’autorégulation de la force des barres explique la grande variété des morphologies galactiques observées.
Comme la plupart des galaxies sont barrées, il faut admettre un processus de reformation de ces barres : l’accrétion de gaz externe en est responsable. Ainsi, plusieurs barres se forment successivement au cours de l’évolution d’une galaxie. Les cycles de formations et de destructions des barres conduisent à une concentration supérieure du gaz au centre de la galaxie, et à la formation des bulbes. Ce mécanisme alimenterait aussi le trou noir tapi au cœur de la plupart des galaxies. Ces dernières années, les images à haute résolution du télescope spatial Hubble ont révélé, au sein de nombreuses galaxies proches, la croissance simultanée de la masse du bulbe et de celle du trou noir supermassif. La précipitation du gaz vers le centre de la galaxie expliquerait cet effet. Une preuve que les simulations ont un pouvoir prédictif et explicatif…
Quelques références vous sont proposées pour en savoir plus sur l’évolution des galaxies.
En français
- Françoise Combes, Des vagues dans la mare galactique, Pour la Science n° 337, novembre 2005.
- F. Bournaud & F. Combes, Le bain de jouvence des galaxies.
En anglais
- F. Bournaud, F. Combes & B. Semelin, The life-time of galactic bars : central mass concentrations and gravity torques.
- F. Bournaud & F. Combes, Gas accretion on spiral galaxies : bar formation and renewal, 2002.
- The Horizon Project.
Une première version de cet article est parue dans le dossier n°52 La modélisation informatique, exploration du réel de la revue Pour la Science, numéro de juillet/septembre 2006.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Françoise Combes
Auparavant astronome à l’Observatoire de Paris et présidente du Programme national « Galaxies » du CNRS (2001-2008). Professeure au Collège de France à la chaire « Galaxies et cosmologie » et lauréate de la médaille d'or 2020 du CNRS.