L’effet papillon n’existe plus !

Contrairement à une idée très répandue, le battement d’une aile de papillon ne déclenche pas de tempête. Des effets statistiques entrent en jeu dans l’atmosphère : la turbulence s’organise et la sensibilité aux conditions initiales disparaît. Par conséquent, on peut espérer prédire le temps qu’il fera au-delà de la limite fatidique de deux semaines avancée par E. Lorenz, météorologiste à l’origine de l’effet papillon. Infographie : Delphine Bailly.

La sérénité de l’Olympe étant réservée aux dieux, les humains tentent depuis longtemps de deviner quel morceau du ciel risque de leur tomber sur la tête. En deux millénaires, les systèmes de prévision sont passés de la consultation des oracles, fondés sur le sacrifice animal, voire humain, aux modèles théoriques et aux calculs numériques.

La mécanique céleste était au centre des préoccupations scientifiques du XIX^e siècle, et la prévision météorologique prend son essor au XX^e siècle. Elle se heurte à des difficultés sérieuses, liées à la modélisation des phénomènes atmosphériques, ainsi qu’au traitement des équations obtenues, qui sont complexes. Face à ces obstacles, l’optimisme qui régnait dans les années 1950 se mue au cours des années 1960 en un pessimisme excessif, qui tient en un seul nom, charmant au demeurant : l’effet papillon.

Le déterminisme laplacien

Dans la longue histoire de la prévision, qu’elle traite du temps ou des mouvements célestes, un moment crucial est la découverte par Isaac Newton au XVII^e siècle des équations qui régissent le mouvement des planètes : connaissant la position et la vitesse des planètes à un instant donné, on détermine les points de leur trajectoire à tout instant ultérieur. Comme tous les systèmes mécaniques obéissent à des équations du même type, l’état initial d’un système détermine complètement son avenir. Cette idée est popularisée par Laplace, au point de devenir une idéologie : le déterminisme laplacien, selon lequel rien de neuf ne peut advenir qui ne soit déjà contenu dans les conditions initiales. Le problème de la prévision semble dès lors résolu, du moins en théorie.

Dans la seconde moitié du XIX^e siècle, le déterminisme laplacien est mis à mal quand des mathématiciens entreprennent de calculer les trajectoires des astres. Henri Poincaré puis Jacques Hadamard découvrent alors que des systèmes pourtant simples, comme celui constitué de trois corps qui s’attirent par gravitation, donnent lieu à des trajectoires très compliquées et que, pour beaucoup de systèmes, la moindre variation des positions ou des vitesses initiales engendre des écarts de trajectoire considérables. Comme l’état initial n’est jamais connu avec une exactitude parfaite, on ne peut déterminer l’évolution d’un tel système au-delà d’un certain temps. Ces travaux sont les prémices de la théorie du chaos, qui se développe à partir des années 1970 et étudie l’évolution de l’incertitude sur l’état initial. À partir des années 1980, les astronomes montrent qu’il est impossible de connaître l’état du système solaire au-delà de quelque 100 millions d’années. Cet horizon dépassé, il faudrait tenir compte, dans les calculs, de la forme des astres, des effets des marées, et d’une multitude d’autres paramètres… Cette découverte ébranle beaucoup le déterminisme laplacien.

Revenons à la météorologie : dans les années 1950, la prévision météorologique « moderne », entreprise scientifique ambitieuse, commence à se mettre en place. Elle associe la physique de la modélisation de l’atmosphère, les mathématiques, le calcul numérique et l’informatique. Au début des années 1960, les premiers ordinateurs performants apparaissent et permettent des calculs jusqu’alors inaccessibles.

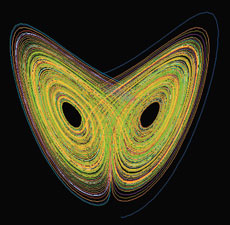
L’attracteur de Lorenz décrit l’évolution d’un système sensible aux conditions initiales. L’état du système est représenté par un point dans l’espace. Deux points initialement voisins ont des trajectoires qui se séparent rapidement et ont des comportements différents. D’un point de vue physique, une petite erreur sur la mesure de l’état initial engendre une incertitude importante sur la connaissance de l’état ultérieur. Image : Temple University

Le météorologiste américain Edward Lorenz commence alors à étudier un modèle simplifié de la convection atmosphérique, fondé sur des équations classiques de la convection dans les fluides. Son modèle contient trois degrés de liberté, c’est-à-dire trois inconnues, et se résume à trois équations différentielles à trois variables. En essayant de prévoir l’évolution de son modèle sur un temps long, il constate qu’il est impossible de la calculer avec précision, car la moindre perturbation initiale du système a un effet considérable à long terme et aboutit à une incertitude sur son état futur, qui croît de façon exponentielle avec le temps. En outre, en représentant l’état du système par un point mobile dans l’espace, il observe que ce point décrit au cours du temps une courbe qui semble s’enrouler autour d’un objet de structure complexe, qualifié d’« attracteur étrange » et aujourd’hui nommé « attracteur de Lorenz ».

E. Lorenz s’attaque ensuite au problème de la circulation atmosphérique à grande échelle. Vue de loin, l’atmosphère apparaît comme une mince pellicule de gaz entourant la sphère terrestre. E. Lorenz considère, en première approximation, qu’il s’agit d’un fluide parfait, c’est-à-dire sans viscosité (à grande échelle, la viscosité moléculaire du gaz joue en effet un rôle négligeable), et à deux dimensions. Il n’utilise qu’un petit nombre de degrés de liberté (quelques dizaines), afin de simplifier les calculs. À nouveau, E. Lorenz retrouve le phénomène de sensibilité exponentielle par rapport aux conditions initiales : la taille d’une perturbation double à chaque fois que le temps augmente d’une valeur donnée. Il pense alors que, si l’avenir est aussi difficile à prédire avec un petit nombre de degrés de liberté, la situation ne peut qu’empirer avec un modèle plus réaliste de l’atmosphère, qui comporterait un grand nombre de degrés de liberté (la pression atmosphérique, les composantes de la vitesse du vent, le taux d’humidité, etc., sont autant d’inconnues à définir en tout point de la Terre).

L’effet papillon sort de son cocon

Avec ces travaux, E. Lorenz retrouve des constatations déjà établies par Poincaré et Hadamard : on ne peut pas toujours calculer l’évolution d’un système simple. Sa contribution est d’avoir montré que l’imprédictibilité concerne non seulement la mécanique céleste, mais aussi les écoulements atmosphériques.

Un contradicteur inconnu fait alors remarquer à E. Lorenz que, si le mouvement de l’atmosphère est aussi instable qu’il le prétend, il suffirait du battement de l’aile d’une mouette pour changer irrémédiablement son évolution. E. Lorenz continue malgré tout à soutenir cette hypothèse et calcule que ce changement se produirait en deux semaines environ. De cette polémique, la mouette se transformant en papillon, naît l’« effet papillon » : un événement, tel le battement des ailes d’un papillon en un point de la Terre, est une perturbation suffisante pour déclencher, deux semaines plus tard, une tornade en un point éloigné. Comme on ne peut connaître l’état de tous les papillons à un instant donné, la prévision de l’état de l’atmosphère au-delà de 15 jours est impossible.

À la même époque, le mathématicien Vladimir Arnold, de l’Institut de mathématiques Steklov, à Moscou, développant des idées de son maître, Andreï Kolmogorov, établit un lien entre l’hydrodynamique d’un fluide parfait et les surfaces à courbure négative (rayons de courbure principaux de signes opposés) d’Hadamard. Ces surfaces présentent, en tout point, un profil en forme de selle de cheval. Considérons une petite bille qui glisse sans frottement sur une telle surface. À partir d’un point quelconque où on la dépose, la bille, lancée avec une certaine vitesse initiale, décrit une trajectoire bien définie. L’ensemble des trajectoires que l’on obtient en modifiant la position de départ et la vitesse initiale est nommé « flot géodésique ». Hadamard a montré que le mouvement d’une bille sur une surface à courbure négative est exponentiellement instable : quand on déplace légèrement son point de départ ou que l’on modifie un tant soit peu sa vitesse initiale, la nouvelle trajectoire s’écarte très rapidement de l’ancienne (la bille peut glisser d’un côté ou de l’autre de la selle par exemple). En pratique, on ne peut pas calculer la trajectoire de la bille au-delà d’un temps court.

V. Arnold ramène le problème de l’instabilité hydrodynamique à un « simple » calcul de courbure. Son idée consiste à décrire le mouvement du fluide parfait comme celui d’un point sur une « surface » ; la surface en question est particulière, puisqu’elle possède une infinité de dimensions (on peut néanmoins, comme sur une surface ordinaire, définir sa courbure et le flot géodésique). En d’autres termes, la vitesse du vent à chaque instant et en tout point de l’atmosphère est décrite par le déplacement d’une bille sur cette « surface », soit le flot géodésique. V. Arnold parvient même à calculer la courbure d’une telle « surface » et montre que les mouvements des fluides parfaits sont analogues aux flots géodésiques d’Hadamard. La situation est plus compliquée, mais ces calculs indiquent le plus souvent que les trajectoires de particules fluides, voisines à l’instant initial, s’écartent l’une de l’autre exponentiellement avec le temps.

Examinons l’état des connaissances à la fin des années 1960. Aux constatations de la fin du XIX^e siècle de Poincaré et d’Hadamard sur la sensibilité des systèmes dynamiques aux conditions initiales, s’ajoutent deux résultats : les simulations numériques de E. Lorenz sur la circulation atmosphérique, qui portent sur trois, puis sur quelques dizaines de degrés de liberté ; et ensuite, l’étude théorique de V. Arnold d’un système doté d’un nombre infini de degrés de liberté, qui montre l’instabilité exponentielle des trajectoires des particules fluides. Ces résultats, joints aux difficultés pratiques de la prévision météorologique, font naître l’idée que les mouvements de l’atmosphère sont impossibles à prévoir, à cause de la sensibilité exponentielle aux conditions initiales : le célèbre « effet papillon » prend son envol. L’image, à la fois poétique et facile à comprendre, se répand dans le grand public et devient le nouveau paradigme qui remplace le déterminisme laplacien. Il diffuse vers d’autres disciplines (économie, sociologie, etc.), et nous invite à repenser le monde en termes « modernes » de chaos, de complexité et d’imprédictibilité. Pourtant, l’effet papillon ne résiste pas à une analyse plus poussée.

L’effet papillon bat de l’aile

Au cours des dernières décennies, les météorologistes ont étudié comment une erreur initiale se propage dans les modèles de prévision du temps ; ils ont constaté qu’après une période de un à deux jours, la croissance des perturbations est, non pas exponentielle, comme l’avait prédit E. Lorenz, mais proportionnelle au temps. Voilà une observation en désaccord avec l’effet papillon. D’où vient la contradiction ?

Dans sa démarche, le météorologue américain fit une erreur. Plus précisément, il se livra à une extrapolation hasardeuse qui le conduisit à des conclusions erronées. En effet, il ne tint pas compte des nouveaux phénomènes d’origine statistique susceptibles d’apparaître lorsqu’on passe d’un petit à un grand nombre de degrés de liberté. C’est le fondement de la mécanique statistique, que découvrit Boltzmann à la fin du XIX^e siècle. Prenons un exemple connu : considérons quatre ou cinq molécules de gaz enfermées dans une boîte. Elles interagissent entre elles et avec les parois de la boîte qui les contient. Pour décrire le comportement de ce petit système à long terme, on se heurte à la même difficulté de calcul que celle rencontrée par E. Lorenz : on ne peut pas prévoir les trajectoires des molécules. Considérons maintenant le système formé par toutes les molécules de gaz présentes dans une pièce. Si l’on voulait décrire avec précision le mouvement de toutes les molécules, la tâche serait insurmontable. En revanche, si l’on s’intéresse seulement à des valeurs moyennes, comme la densité, la pression et la température, on s’aperçoit que ces quantités statistiques sont prévisibles à long terme : on peut, par exemple, prédire avec un risque d’erreur minime que la densité va rester uniforme et constante dans toute la pièce. La cause apparaît dans le scénario imaginé par Boltzmann : si le système est suffisamment chaotique, les molécules ont tendance à occuper tout l’espace disponible. Autrement dit, même si l’on plaçait initialement toutes les molécules dans un coin de la pièce, elles ne resteraient pas confinées, à cause de leurs mouvements erratiques (aléatoires). On parle d’« observables macroscopiques » pour désigner ces moyennes statistiques, telle la pression, par opposition aux trajectoires individuelles des molécules, qui sont des « observables microscopiques ».

Résumons la leçon de Boltzmann : avec un grand nombre de degrés de liberté, bien que le système ne soit pas microscopiquement prévisible, les observables macroscopiques le sont. Avant d’aller plus loin, faisons une incursion dans le domaine de la turbulence, puisque l’atmosphère est un fluide turbulent.

Turbulence et structures cohérentes

La turbulence, mouvement complexe et désordonné d’un fluide, apparaît dans presque tous les écoulements, sauf lorsque le frottement visqueux (frottement des molécules les unes sur les autres) domine. Dans ce cas, l’écoulement prend un aspect plus ordonné, et on dit qu’il est laminaire. En pratique, les écoulements observé à l’échelle humaine (les rivières, les courants d’air…) sont turbulents, de même que l’écoulement atmosphérique ou océanique.

Tourbillons autour du pôle Sud. Antycyclones ou dépressions, ces tourbillons ou structures cohérentes, naissent de l’organisation de la turbulence atmosphérique. Image : NASA

Nous nous intéressons à la classe particulière d’écoulements turbulents à deux dimensions, c’est-à-dire ceux qui ont lieu dans un plan ou sur une surface. Cela n’est pas une vue de l’esprit, mais une approximation justifiée pour un fluide contenu dans un récipient en rotation rapide, ou pour un fluide confiné dans une couche de faible épaisseur. Les mouvements de l’atmosphère et des océans sont considérés comme des écoulements bidimensionnels, car l’épaisseur des fluides est négligeable par rapport à leur étendue.

Nous faisons aussi l’hypothèse que l’écoulement de l’atmosphère est incompressible, ce qui est vérifié à l’échelle globale dans l’atmosphère et dans les océans. Dans ce cas, la dynamique de l’écoulement est déterminée par une grandeur définie en chaque point du fluide : la « vorticité ». Elle mesure la vitesse de rotation propre de chaque point du fluide (en termes mathématiques, la vorticité est le rotationnel de la vitesse) : chaque point est représenté par une petite toupie qui tourne sur elle-même. Le fluide est constitué d’une multitude de toupies, mais toutes n’ont pas la même vitesse de rotation. Quand le fluide s’écoule, elles se déplacent. Dans les écoulements que nous étudions, la vorticité d’une particule fluide reste inchangée, c’est-à-dire que les toupies gardent toujours les mêmes vitesses de rotation, car les frottements par viscosité sont négligeables.

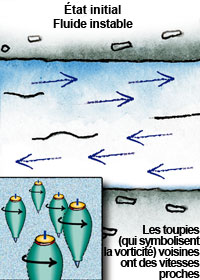
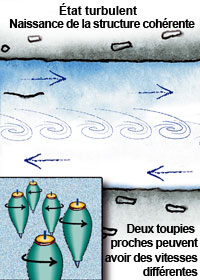
Dans un fluide parfait incompressible à deux dimensions (l’atmosphère par exemple), l’écoulement est décrit par la vorticité : à chaque point est associée une minuscule « toupie » qui est emportée par le flot, tout en conservant sa vitesse de rotation. Dans l’état initial (à gauche), deux points voisins ont des vorticités proches : les toupies associées tournent à peu près à la même vitesse. Comme deux courants se croisent, l’état est instable et l’écoulement devient turbulent (au centre) ; deux points proches ont parfois des vorticités différentes. À l’échelle microscopique, on ne peut prévoir la vorticité de tous les points. Pourtant, l’ordre émerge de ce chaos et, à l’échelle macroscopique, l’écoulement fluide s’organise en structures cohérentes (à droite, un tourbillon simple). L’ordre semble régner alors que le chaos subsiste à petite échelle. Infographie : Pour la Science

Vue de Jupiter prise par la sonde Voyager 1. Jupiter est une planète géante gazeuse. Un gigantesque tourbillon d’environ 20 000 kilomètres de diamètre occupe une couche superficielle de 100 kilomètres d’épaisseur dans son atmosphère. Galilée déjà avait repéré cette grande tache rouge. La persistance de ce tourbillon dans une atmosphère turbulente animée de vents très violents (de l’ordre de 300 kilomètres par heure) est restée longtemps mystérieuse. Il s’agit en fait d’une structure cohérente de la turbulence bidimensionnelle, les ovales blancs étant des tourbillons de plus petite taille. Image : NASA

Alors qu’à petite échelle, le mouvement est chaotique, on observe qu’à grande échelle, les écoulements turbulents bidimensionnels incompressibles s’organisent, et de grandes structures tourbillonnaires apparaissent. Ces « structures cohérentes » sont formées d’un seul tourbillon, ou de deux, accolés et tournant en sens inverse, ou encore de trois, ou plus. Elles s’étendent sur plusieurs milliers de kilomètres dans l’atmosphère terrestre, où l’on en observe tous les jours grâce aux nuages qui apparaissent sur les images prises par satellite. Plus loin de nous, la tache rouge de Jupiter, gigantesque tourbillon d’environ 20 000 kilomètres de diamètre, formé dans une mince couche fluide à la surface de la planète, est un exemple spectaculaire d’une telle structure.

La formation systématique de telles structures cohérentes est une caractéristique des écoulements à deux dimensions. Elles apparaissent et persistent au sein d’écoulements très chaotiques, ce qui a longtemps intrigué les observateurs. Pourquoi ne sont-elles pas disloquées par la turbulence vigoureuse où elles baignent ?

Un tourbillon, dans une rivière par exemple, se caractérise localement par une vorticité élevée, c’est-à-dire que de nombreuses toupies tournant dans le même sens se regroupent dans une même région. Mais cette description ne suffit pas à nous faire comprendre l’organisation des systèmes tourbillonnaires cohérents. En effet, les tourbillons interagissent de façon complexe, et éclatent parfois en de multiples fragments. Cependant l’écoulement finit par s’organiser en quelques structures simples qui persistent dans le temps, tel l’anticyclone des Açores qui se déforme et se déplace, mais reste toujours plus ou moins dans la même région. Grâce à des simulations numériques menées au cours des 20 dernières années, on a pu reproduire l’apparition de tourbillons stables au sein d’un écoulement turbulent.

En 1949, le physicien américain Lars Onsager remarque que l’énergie cinétique du fluide est conservée dans un écoulement turbulent bidimensionnel. Il suggère alors que les tourbillons stables devraient être décrits comme des états d’équilibre statistique, en étendant la mécanique statistique de Boltzmann au fluide parfait. L’entreprise s’est longtemps heurtée à des difficultés théoriques. Le problème se résout quand on introduit deux niveaux de description du mouvement fluide. Le premier niveau, macroscopique, concerne le mouvement à grande échelle, c’est-à-dire vu de loin, et ignore les détails (il se situe à l’échelle du millier de kilomètres pour l’atmosphère terrestre) ; quant au niveau microscopique, il décrit ce qui se passe à petite échelle (quelques dizaines de kilomètres), à l’échelle où s’épanouit le chaos turbulent. Suivant la démarche de Boltzmann, on définit une entropie, une grandeur qui quantifie le désordre, ici lié à la turbulence : l’entropie statistique d’un état macroscopique s’obtient en comptant le nombre d’états microscopiques possibles de l’état considéré. Elle est d’autant plus élevée que le nombre d’états microscopiques – et donc le désordre – est important. On cherche ensuite les états macroscopiques du système les plus probables, c’est-à-dire ceux qui rendent l’entropie maximale. Ces états de l’atmosphère correspondent aux structures tourbillonnaires cohérentes.

Décrivons plus précisément le scénario de formation des structures cohérentes. Dans l’état initial, la vorticité varie de façon régulière d’un point du fluide à son voisin : des toupies proches tournent à des vitesses similaires. L’écoulement turbulent crée un mouvement complexe à petite échelle. À mesure que la turbulence se développe, les toupies de différentes vitesses de rotation se mélangent. La vorticité oscille alors de façon chaotique, quand on passe d’un point à un autre, voisin : une toupie qui tourne lentement jouxte une autre dont la rotation sur elle-même est très rapide. Il est impossible de prévoir les vorticités des points du fluide. Pourtant, ces oscillations incohérentes de la vorticité à petite échelle entraînent la formation des structures à grande échelle.

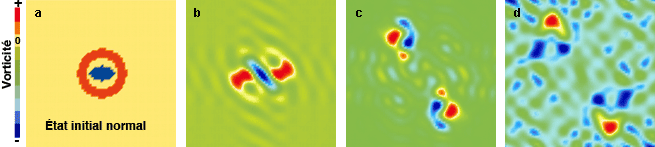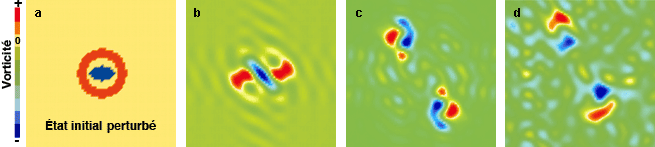
L’évolution de l’atmosphère est simulée avec un modèle d’écoulement identique à celui utilisé par E. Lorenz. À chaque point du plan est associée une « toupie », sa vorticité. Les valeurs sont indiquées par des couleurs allant du bleu (la vorticité est négative : la toupie tourne dans le sens des aiguilles d’une montre) au rouge (la vorticité est positive : la toupie tourne dans le sens contraire), en passant par le jaune (la vorticité est nulle). L’état initial (a) est choisi de façon à ce que le système évolue rapidement vers une structure cohérente : il a une forme particulière, constituée d’une ellipse où la vorticité est négative, entourée d’une couronne où la vorticité est positive (il n’existe pas d’état initial de l’atmosphère, mais on sait que de telles structures cohérentes se forment). Le calcul est effectué avec un faible nombre de variables (de l’ordre de 100) ; les « points » qui constituent l’atmosphère sont épais et les figures sont floues. Après une courte période d’évolution, trois tourbillons apparaissent (b), puis se fragmentent (c), et l’atmosphère devient de plus en plus chaotique (d). On perturbe légèrement l’état initial : la perturbation étant faible, rien n’est visible à l’œil nu au début (a et b) ; un examen attentif (c) révèle de légères différences avec la phase correspondante du modèle initial (non perturbé). Ensuite, le système perturbé (d) évolue différemment du système non perturbé. Pour un tel système, l’évolution à long terme n’est pas prévisible.
Images : R. Robert / C. Rosier

Le passage de la vorticité (une variable microscopique) au champ de vitesses de l’atmosphère (une variable macroscopique) est analogue à celui qui mène du mouvement des molécules gazeuses à la pression : le déplacement chaotique des molécules pousse ces dernières à remplir uniformément l’espace, et la pression provient des chocs contre les parois. On déduit sa valeur du nombre moyen de collisions contre les parois : elle prend une valeur bien déterminée, uniforme dans la pièce. De même, on déduit le champ de vitesses de l’écoulement de la moyenne statistique des vorticités. Le champ de vitesses ainsi calculé n’est pas uniforme, mais il fait apparaître des tourbillons organisés.

L’introduction de la mécanique statistique dans l’étude des écoulements à deux dimensions montre que le champ de vitesses (une variable macroscopique) est théoriquement prédictible. Cela contredit-il les calculs de V. Arnold ? Non, car ses calculs montrent que les trajectoires (microscopiques) des particules fluides divergent, éparpillant les toupies dont la vitesse de rotation est lente parmi celles qui tournent très vite. Ce phénomène provoque les oscillations chaotiques de la vorticité à petite échelle, qui engendrent, en fin de compte, un champ de vitesses prédictible au niveau macroscopique.

Prévisions à long terme

Nous avons validé cette approche théorique en effectuant des simulations numériques sur l’équation du fluide parfait à deux dimensions et en utilisant un très grand nombre de degrés de liberté. Autrement dit, nous refaisons les calculs de E. Lorenz, mais avec un grand nombre de degrés de liberté, au lieu de quelques dizaines.

Pour faire le calcul, nous choisissons une condition initiale, déterminée par la vorticité en tout point, puis nous laissons évoluer le système. Cet état initial engendre des structures organisées, après une phase de transition assez rapide. En faisant varier l’état initial, nous obtenons deux types d’état final : soit une structure cohérente tripolaire, c’est-à-dire trois tourbillons accolés animés d’un mouvement global de rotation uniforme, soit quatre tourbillons formés de deux paires de tourbillons accolés, tournant en sens opposés, chaque paire se propageant en ligne droite à vitesse uniforme. De telles structures sont observées dans l’atmosphère ou les océans.

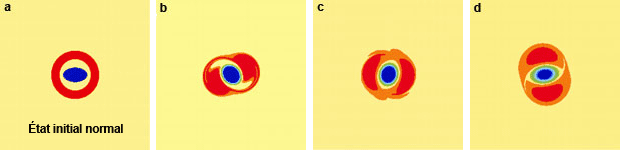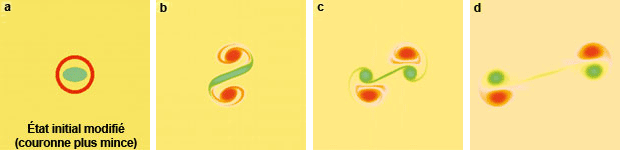
Avec un grand nombre de variables (de l’ordre de 100 000), la simulation de l’atmosphère diffère de celle que prévoit le modèle de Lorenz : l’atmosphère s’organise, car des effets statistiques interviennent. Au début, la couronne se déforme et s’enroule autour de l’ellipse ; progressivement un système formé de trois tourbillons se constituent, puis se stabilise en une structure formée d’un tourbillon central entouré de deux tourbillons accolés tournant en sens inverse, le tout étant animé d’un mouvement de rotation uniforme. On aboutit donc non plus à un système chaotique, mais à une structure cohérente stable. En changeant l’état initial (couronne plus mince), on observe une organisation différente : le tourbillon central s’étire, puis le système se scinde en deux dipôles qui s’éloignent l’un de l’autre à vitesse constante. Dans les deux cas, une légère perturbation (non représentée ici) de l’état initial a un effet très faible, impossible à détecter à l’œil nu : on n’observe pas de sensibilité par rapport aux conditions initiales et l’on peut prévoir l’évolution. Les simulations numériques présentées ici ont été effectuées par Carole Rosier de l’Université de Lyon 1.
Images : R. Robert / C. Rosier

Qu’en est-il de l’effet papillon ? Effectuons sur les simulations précédentes une petite perturbation des conditions initiales. Dans le premier cas, qui mène à la formation de trois tourbillons, la perturbation n’a aucun effet sur la formation de la structure : on retrouve les trois mêmes tourbillons accolés. Quand on calcule l’évolution dans le temps de l’énergie de la perturbation, on constate qu’elle se stabilise et reste faible par rapport à l’énergie totale du système. Dans le deuxième cas non plus, la perturbation n’entraîne aucun effet visible, et l’on retrouve les deux paires de tourbillons. En revanche, l’énergie de la perturbation augmente linéairement avec le temps. Il existe un troisième cas exceptionnel, critique, à la frontière des deux cas précédents, où le système « hésite » entre les deux états finaux. Dans ce cas, et dans ce cas seulement, les systèmes perturbés et non perturbés ont des comportements distincts. L’énergie de la perturbation évolue au début comme dans les deux premiers cas, puis entre brusquement dans une phase de croissance exponentielle. On constate donc que l’instabilité exponentielle apparaît seulement dans cette situation exceptionnelle dite de « transition de phase », où le système hésite entre deux chemins possibles.

Si nous refaisons ces calculs en diminuant seulement le nombre de degrés de liberté (toutes choses égales d’ailleurs), on constate qu’aucune structure cohérente ne se forme, mais qu’un chaos turbulent apparaît et se propage dans tout l’espace, cependant que l’énergie de la perturbation croît rapidement pour devenir comparable à l’énergie du système ; on retrouve alors bien les observations de E. Lorenz.

Ces simulations numériques montrent que le système évolue différemment suivant le petit ou grand nombre de degrés de liberté que l’on prend en compte : bien que, à cause de la turbulence à petite échelle, les trajectoires des particules fluides soient chaotiques et imprévisibles, on peut prévoir le champ des vitesses du fluide, c’est-à-dire qu’il n’est pas exponentiellement sensible aux petites variations des conditions initiales (sauf situation exceptionnelle).

On pourra objecter que l’atmosphère terrestre est bien plus complexe que le fluide parfait à deux dimensions étudié ici. À cela, nous répondons, d’une part, que c’est en considérant ce même système que E. Lorenz aboutit à une conclusion opposée ; d’autre part, les modèles complexes, qui décrivent de manière plus réaliste l’écoulement atmosphérique, possèdent les mêmes propriétés que l’équation du fluide parfait bidimensionnel (le chaos à petite échelle, l’imprédictibilité des trajectoires des particules fluides et la formation de structures cohérentes).

L’étude de sensibilité aux conditions initiales présentée ici porte sur un mécanisme d’auto-organisation particulier, qui, bien qu’il ait été choisi pour son caractère instable, n’épuise pas à lui seul tous les comportements possibles des écoulements bidimensionnels. Il est cependant représentatif du type de phénomènes que l’on observe dans la circulation atmosphérique, formée de structures cohérentes qui se déplacent autour de la planète et interagissent, tels les anticyclones ou les dépressions. D’autres simulations numériques font apparaître le même phénomène que nous avons mis en évidence : la croissance de l’énergie de la perturbation est le plus souvent linéaire, très rarement exponentielle, en accord avec les observations des météorologistes. En conséquence, le pronostic de prévision change : l’erreur de prévision ne double pas à chaque fois que le temps augmente d’une valeur donnée, comme le prévoit E. Lorenz, mais elle croît linéairement (elle double quand le temps double). Les prévisions à deux semaines, annoncées par E. Lorenz, ne constituent pas une limite fatidique. La prévision à long terme devient possible si l’on améliore la connaissance de l’état initial de l’atmosphère. On peut donc s’attendre à des progrès importants de la fiabilité des prévisions dans les années à venir, grâce à des ordinateurs plus puissants, à un maillage plus serré du réseau d’observations et à des modèles plus perfectionnés. Cependant, cet optimisme doit être tempéré ; comme on l’a vu, des difficultés demeurent à cause des situations critiques où le système peut basculer vers une structure ou vers une autre. Les prévisions locales, comme les orages, sont encore plus difficiles à établir, car elles doivent en plus prendre en compte les détails du relief.

L’effet papillon est invoqué à tout propos, même en économie ou en sociologie, quand on cherche à souligner l’incapacité de prédire les conséquences d’infimes perturbations. Retenons de ce qui précède que dans les systèmes complexes, qui possèdent un grand nombre de degrés de liberté, et où l’on se préoccupe de prédire des quantités « macroscopiques », qui sont des moyennes statistiques, l’instabilité exponentielle du système « microscopique » n’est pas synonyme d’imprédictibilité.

Quelques références vous sont proposées pour en savoir plus sur l’effet papillon.