La riche zoologie des automates cellulaires

La voiture qui vous précède a avancé d’une longueur, vous avancez pour occuper sa place. Évidemment, vous n’auriez pas pu bouger si elle était restée immobile. Ces comportements banals constituent l’essence même d’un embouteillage : la lente progression du train de voitures résulte de la répétition de quelques comportements machinaux adoptés par des milliers d’automobilistes. Dès lors, comment modéliser la propagation d’un bouchon ? La physique compliquée du contact de la gomme des pneus avec la route est aussi peu pertinente que la psychologie du conducteur. Une démarche efficace est de diviser la route en une succession de « cellules » hébergeant chacune un véhicule, puis d’écrire les quelques « règles » exprimant les comportements possibles des conducteurs.

Une cellule occupée par un véhicule est en noir, une cellule vide en bleu, et l’occupation de la route à un moment donné sera figurée par une ligne comme ci-dessous :

L’évolution de la circulation sera représentée par un empilement (progressant vers le haut) de telles lignes représentant l’évolution du trafic, le passage d’une ligne à la suivante obéissant à un certain nombre de règles. Pour une route simple, il y a huit règles du type indiqué ci-dessous (la cellule centrale est indiquée par un disque blanc).

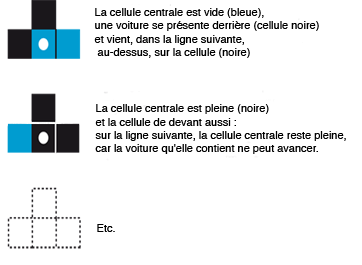
Images : M. Delorme et J. Mazoyer

Chaque état de la route est calculé par l’ordinateur en appliquant ces règles à l’état précédent. En une fraction de seconde, le tableau ci-contre apparaît, où la propagation de bouchons se traduit par la progression vers la gauche de bandes noires (ce qui illustre que les bouchons se propagent selon une onde rétrograde vers l’arrière du trafic). Notre modèle dynamique de la circulation constitue un exemple d’automate cellulaire, c’est-à-dire d’une société de cellules élémentaires, dont chacune se transforme, étape après étape, en l’un des quelques états possibles, déterminé en fonction des états d’un nombre réduit de cellules voisines (ici trois cellules). Pour définir un automate cellulaire, on donne la disposition de ses cellules (son espace), quelles cellules voisines ont un effet sur une cellule (son voisinage) et les règles qui définissent son évolution. Ces règles locales, qui ne mettent en jeu qu’un nombre fini de voisines d’une cellule, ont un effet global : elles déterminent la dynamique de la société de cellules toute entière.

Complication ou complexité

Nous examinerons ici la riche zoologie des automates cellulaires, qu’il serait souhaitable de classer par degrés de complexité en fonction des structures qu’ils produisent. Ce problème difficile n’a que des solutions partielles ; toutefois, nous savons distinguer les automates qui engendrent des structures seulement « compliquées » de ceux qui en produisent de « véritablement complexes ». Nous montrerons que, dans certains cas, toute la complexité des automates est représentée dans une structure unique, celle des automates « intrinsèquement universels ».

Les automates cellulaires simulent les phénomènes qui s’auto-organisent, telles des gouttes de pluie sur une vitre (en haut).
Image : M. Delorme et J. Mazoyer

Pourquoi importe-t-il de maîtriser la complexité produite par les automates cellulaires ? Comparés à la réalité, les automates cellulaires paraissent simplistes. Pourtant, ils sont devenus incontournables pour simuler les effets des nombreux phénomènes qui s’auto-organisent. En physique, le modèle d’Ising décrit le ferromagnétisme en réduisant la complexité des atomes à des flèches plantées au milieu de cellules qui n’interagissent qu’avec leurs plus proches voisines ; inventé en 1925, ce modèle constitue l’un des tout premiers automates cellulaires. Un grand producteur de cosmétiques utilise une société d’« automates folliculaires » pour simuler la croissance des cheveux et tester les effets globaux de l’action d’un cosmétique sur l’une des trois phases du cycle folliculaire. La propagation des grands incendies de l’été 2003 dans le massif des Maures est modélisée par quelques règles qui déterminent la combustion des cellules forestières à l’avant en fonction des cellules qui s’embrasent à l’arrière.

Il existe aussi des automates cellulaires qui simulent le comportement des gaz, la cristallisation des solides, la fuite d’une foule devant un danger ou, ce qui revient au même, l’écoulement du sable, la turbulence au sein des liquides, le développement urbain, la percolation, etc. Dans chaque cas, leur usage réduit la complexité de la situation à ce qui est nécessaire pour engendrer la dynamique du phénomène. C’est là un paradoxe : la réalité est complexe alors que, souvent, les lois qui la gouvernent ne le sont pas ! En pratique, les automates cellulaires se prêtent bien à la simulation numérique. Une bonne simulation suppose de la puissance de calcul, mais cette puissance nécessaire est moindre quand les calculs à effectuer peuvent être faits simultanément, c’est-à-dire en parallèle. Or, la nature locale des interactions des cellules rend la programmation d’un automate cellulaire facile à « paralléliser ». L’utilisation toujours plus fréquente, dans les jeux vidéo ou autres programmes graphiques, d’éléments qui simulent la réalité, nous confrontera de plus en plus à des programmes fondés sur des automates cellulaires. Comment se comportent ces automates ? Comment appréhender la complexité des structures qu’ils engendrent ?

Les classes de Wolfram

Stephen Wolfram fut l’un des premiers chercheurs à réaliser l’importance de cette question. En 1984, il proposa de distinguer quatre « classes de complexité » d’automates cellulaires en fonction des propriétés de leurs « orbites ». On nomme ainsi le diagramme, dit aussi diagramme espace-temps, obtenu en empilant les représentations des configurations engendrées successivement par un automate à partir d’une configuration initiale, comme nous l’avons fait pour la circulation.

Selon nous, les classes de complexité de Wolfram ne suffisent pas à rendre compte de la complexité des automates cellulaires ; toutefois, nous les utiliserons pour explorer progressivement les degrés de complexité rencontrés. Afin de les expliciter ainsi que toutes les notions abordées ici, nous examinerons les exemples d’orbites fournis par un type simple d’automate cellulaire, les « automates cellulaires élémentaires ». Leur espace est une ligne de cellules, chaque cellule pouvant prendre deux états différents, comme les cellules bleues ou noires de notre exemple de la circulation. Les règles locales déterminent l’état suivant d’une cellule en fonction de l’un des huit triplets possibles de trois cellules (la cellule envisagée, sa voisine de droite et celle de gauche) : comme il y a deux possibilités pour chaque cellule (0) ou (1) sur la ligne suivante, il y a 2⁸, soit 256 règles locales que nous dénommons automates élémentaires. Numérotés de 0 à 255, ces automates élémentaires se notent par une succession de huit 0 ou 1 associés à huit triplets donnés toujours dans le même ordre : 111 110 101 100 011 010 001 000 (les 8 triplets sont en fait la notation en base 2 des nombres de 7 à 0).

Ainsi, la règle 184, par exemple, celle précédemment utilisée pour décrire la règle de circulation, est notée (10111000), ce qui s’interprète comme suit :

Un univers limité à 256 habitants semble pauvre, mais ce nombre réduit de règles et le choix de la configuration initiale (la ligne de départ) suffisent à engendrer une infinité d’orbites de complexités variées, couvrant les quatre classes de Wolfram. En outre, ces automates ont l’avantage d’être faciles à visualiser sur une feuille de papier en empilant les lignes successives.

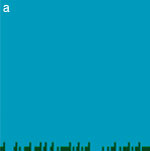
Après une phase transitoire, les automates cellulaires de classe 1 de S. Wolfram produisent des diagrammes espace-temps uniformes (a). Ceux de classe 2 engendrent des diagrammes espace-temps périodiques (b). Les automates cellulaires de classe 3 produisent des diagrammes espace-temps qualifiés de chaotiques (c), tandis que ceux de classe 4 font apparaître des particules (successions de petits triangles) qui semblent animées d’une existence propre. Images : M. Delorme et J. Mazoyer

Le comportement des automates de classe 1 de Wolfram (en a) est monotone : ils convergent vers un champ uniforme qu’ils ne quittent plus. Celui des automates de la classe 2 (en b) est un peu moins banal : ils produisent des orbites périodiques dans le temps. Si la périodicité observée dans le diagramme espace-temps ne fait souvent que refléter celle de la configuration initiale, il existe des automates cellulaires de classe 2 qui produisent des orbites périodiques sans que leur configuration initiale le soit. Les automates de ces classes semblent simples, ce qui est trompeur. Déterminer si un automate appartient à l’une ou à l’autre est un problème indécidable au sens de Gödel : il n’existe aucun algorithme qui, prenant en « entrée » un tel automate, donne en « sortie » son appartenance ou non à la classe.

Comportements inextricables

Les comportements des automates de classes 3 et 4 (respectivement c et d ci-dessus) apparaissent « compliqués » du début à la fin de leur évolution, voire inextricablement complexes. Les règles locales définissant les automates cellulaires ne rendent pas compte de leur puissance. Celle-ci est exprimée dans les évolutions de leurs configurations (leur dynamique). Par automate cellulaire compliqué, mais pas exagérément complexe, nous entendons des automates cellulaires dont nous pouvons structurer mathématiquement l’espace des configurations et décrire certaines propriétés de leur évolution. D’un certain point de vue, les automates cellulaires de classe 3 ne sont ainsi que « compliqués ». En revanche, l’étonnante forme d’ordre local surgissant de façon imprévisible dans tous les automates de classe 4 est plus que « compliquée » : à ce jour, cette forme reste non décrite mathématiquement. Les automates de classe 3 sont souvent qualifiés de chaotiques, car leurs orbites semblent irrégulières. Pour donner un sens à ce terme, on doit déterminer la cause de l’irrégularité observée. Le comportement de certains automates de classe 3 dénote une grande sensibilité aux conditions initiales : une légère modification de la configuration initiale change fortement les orbites ou entraîne des répercussions très lointaines sur certaines orbites.

L’automate cellulaire de la règle 150 (10010110), de classe 3 de S. Wolfram, produit une dynamique compliquée. Les nombreuses particules (triangles) qu’il engendre évoluent suivant leurs propres lois (a). En outre, cet automate est très sensible aux conditions initiales : lorsque, dans la ligne initiale dont les orbites sont issues, on modifie la cellule placée en face de la flèche, une orbite très différente apparaît (b). Curieusement, le diagramme obtenu par différence entre celui de gauche et celui du centre est une organisation fractale de triangles blancs. Images : M. Delorme et J. Mazoyer

Ce comportement évoque le chaos — tel que les physiciens l’entendent, c’est-à-dire qu’un système est chaotique si de « petites modifications lointaines » provoquent des conséquences significatives pour l’observateur (typiquement, l’effet papillon) ; cette notion est différente de l’idée que le chaos est « sans structure » — et invite à l’étude de l’ensemble des configurations afin que nous puissions comparer les orbites de lignes initiales.

Comment s’y prend-on ? On munit l’ensemble des configurations d’une « topologie », en d’autres termes d’une notion de voisinage entre configurations. Pour cela, on définit une distance entre deux configurations, et la plus naturelle est celle énoncée par le mathématicien allemand Georg Cantor (1845-1918) : Plus deux configurations (deux lignes) coïncident près de l’origine (elles ont un grand nombre de cellules dans le même état), plus elles sont « proches ». Grâce à la distance de Cantor, des propriétés significatives des configurations, donc de l’automate, peuvent être définies. Une configuration est, par exemple, « équicontinue » si l’orbite issue d’une configuration proche reste proche au cours de l’évolution. Un automate est dit équicontinu quand toutes ses configurations sont équicontinues. Un automate est dit sensible (aux conditions initiales) quand pour chacune de ses configurations, il existe une configuration proche dont l’orbite s’éloigne de la sienne. Un automate est dit expansif quand les différences entre toutes paires de configurations proches sont amplifiées au cours de l’évolution de l’automate.

Grâce à ces notions, on classe les automates cellulaires en quatre « classes de Kůrka » : la classe des automates équicontinus, celle de ceux qui ne le sont pas mais ont des configurations équicontinues, celle des automates sensibles qui ne sont pas expansifs et celle des automates expansifs. Ainsi, les automates produisant des diagrammes espace-temps très irréguliers sont chaotiques : soit sensibles, soit expansifs. Notons — c’est là l’une des illustrations de l’insuffisance des classes de complexité de S. Wolfram — que certains des automates de la classe 3 de S. Wolfram ne sont pas chaotiques au sens de Kůrka (l’expérimentation sur ordinateur que fait S. Wolfram ne met en jeu que des configurations initiales périodiques – avec de petites périodes –, or certains phénomènes chaotiques n’apparaissent que sur des configurations non périodiques ou pour de très grandes périodes ou, encore, extrêmement rarement).

Notons qu’il existe des alternatives aux classes de Kůrka pour caractériser le type de chaos produit par un automate cellulaire. Toutes, comme celles de Kůrka, intègrent l’idée de sensibilité aux conditions initiales. Ainsi, la multiplicité des points de vue montre qu’il n’y a pas de définition intrinsèque du chaos produit par un automate cellulaire. Toutefois, même si l’irrégularité d’une orbite chaotique est impressionnante, nous ne sommes pas, pour autant, démunis face au chaos. Des moyens de comparer les orbites chaotiques et de ranger les automates qui les produisent en plusieurs classes existent. Ceci suggère que des automates produisant des diagrammes d’espace-temps irréguliers sont seulement « compliqués », plutôt qu’« au-delà du compliqué », c’est-à-dire véritablement complexes. Pour nous, la « véritable complexité » se rencontre au sein de la classe 4. Cela est d’autant plus vrai que l’on ne connaît pas d’automate de la classe 4 qui soit seulement compliqué au sens mathématique indiqué plus haut. Les diagrammes espace-temps des automates de la classe 4 de S. Wolfram présentent une particularité remarquable : au bout d’un certain temps de stabilisation ou d’auto-organisation, des structures, des sortes de particules, apparaissent. C’est le cas des « glisseurs » dans le célèbre Jeu de la vie, l’un des automates cellulaires les plus connus, mais qui n’est pas inclus dans notre étude, car le Jeu de la vie est de dimension deux. Dans notre exemple, les particules ou glisseurs semblent animés d’une dynamique propre : ils se déploient, entrent en collision, se transforment ou non lors de ces chocs et séparent des zones uniformes que l’on interprète comme des fonds.

Les groupages

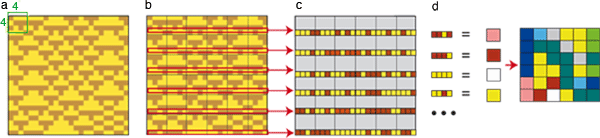
Les techniques de groupage servent à comparer les complexités d’orbites différentes. Elles compriment l’information des orbites pour en extraire des structures sous-jacentes. En (a), un diagramme obtenu avec la règle 54 est d’abord découpé en 36 carrés de cellules 4×4 (b), puis ces carrés sont réduits à leur ligne inférieure (c). De nouvelles règles affectent ensuite des couleurs aux carrés de ces lignes en fonction de leur environnement cellulaire (d), de sorte que le diagramme espace-temps d’un nouvel automate – le groupé de l’automate de départ – apparaît.
Images : M. Delorme et J. Mazoyer

Pour comprendre la dynamique des particules, on les singularise par des techniques comme les groupages, qui font surgir leurs mouvements des diagrammes espace-temps. Comme les motifs des fonds sur lesquels se déplacent les particules se ressemblent et ne diffèrent que par leur position, il suffit de les représenter par un moyen automatique en oubliant leur forme. C’est l’essence des différents types de groupage dont nous donnerons un exemple simple : dans ce groupage, on divise les diagrammes espace-temps d’un automate A en carrés de quatre cellules de côté. Un tel groupage carré contient un motif du fond. On réduit chaque carré à sa ligne inférieure, ce qui n’entraîne pas de perte d’information : à partir des quadruplets de cellules obtenus par groupage, on sait reconstituer tout l’automate cellulaire.

De ces règles se déduit un processus (automatisable) de réduction des diagrammes espace-temps de l’automate initial en nouveaux diagrammes espace-temps. Ces nouvelles orbites sont celles d’un nouvel automate : le « groupé de A » au sens du groupage carré considéré. Sur la figure ci-dessous, nous donnons plusieurs autres exemples de structures qui émergent d’orbites obtenues par la règle 54 (00110110). Dans le premier exemple, on observe une rupture entre deux « fonds », que l’on peut interpréter comme la propagation d’une interface vers la droite. Le diagramme correspondant de l’automate groupé est la juxtaposition de deux zones homogènes ; c’est aussi l’un des diagrammes espace-temps produits par l’automate 170 (10101010). Les diagrammes espace-temps de l’automate 240, qui montrent une interface se propageant vers la droite, et de l’automate 204, qui donne une interface immobile, sont aussi obtenus avec l’automate 54.

L’intérêt du groupage est de faire apparaître les structures sous-jacentes d’un diagramme espace-temps obtenu ici avec la règle 54. Ainsi, ci-dessus en (a), le diagramme groupé révèle une rupture ebtre deux fonds que l’on interprète comme une interface se propageant vers la droite. En (b), une interface semblable se propage vers la gauche. En (c), les pointes d’une succession de particules triangulaires font apparaître une parabole (figurée par les pointillés) entre deux murs de particules verticales, c’est-à-dire immobiles. Images : M. Delorme et J. Mazoyer

Grâce à ces techniques de groupage, on définit des degrés de complexité. Un automate A sera déclaré moins complexe qu’un automate B, si l’ensemble des orbites de l’automate A obtenu par un certain groupage est contenu dans des structures sous-jacentes des orbites de l’automate groupé de B (et ce, quelle que soit la ligne initiale). S’il en est ainsi, c’est bien que les diagrammes groupés de A contiennent moins d’information que ceux de B : ils sont moins complexes. L’automate élémentaire de la règle 240, par exemple, est moins complexe que celui de la règle 54, puisque ses diagrammes espace-temps sont contenus dans ceux produits par la règle 54. Un automate cellulaire étant représenté par l’ensemble de ses diagrammes espace-temps, on en conclut que A est moins complexe que B. Si A est moins complexe que B et si B est moins complexe que A, on identifie A et B. Tous les automates ainsi identifiés déterminent un ensemble, appelé classe (d’équivalence), qui contient en particulier tous les groupés de chacun de ses éléments. On peut alors comparer deux classes entre elles : une classe A est plus petite que B si un quelconque des automates de A est moins complexe que l’un quelconque des automates de B ; on définit ainsi une relation d’ordre partiel (partiel seulement, car il se peut que deux classes A et B ne soient pas comparables selon cette technique).

Orbite d’un automate intrinsèquement universel à six états. Toutes les orbites des automates cellulaires élémentaires peuvent être extraites par groupage des orbites de cet automate.
Images : M. Delorme et J. Mazoyer

Échelles de complexité

L’ensemble des classes au sens d’un groupage peut éventuellement posséder un plus grand élément. Ainsi, tandis que l’ordre induit par le groupage carré ne possède pas de plus grand élément, le groupage rectangulaire conduit à un ordre possédant un maximum : la classe des automates intrinsèquement universels. Nous avons ainsi réussi à distinguer des niveaux de complexité différents pour un groupage donné au sein de la foule des automates cellulaires. L’existence de cet ordre partiel suggère une notion d’éloignement dans la complexité : un automate est d’autant plus loin d’un autre qu’il en est séparé par un plus grand nombre de barreaux dans l’échelle de la complexité. Notons que si une échelle contient une infinité de barreaux, un automate B peut se trouver infiniment éloigné (en complexité) d’un automate A. Seuls certains groupages, tel le groupage rectangulaire, produisent une échelle de complexité (infinie), dotée d’un barreau supérieur : ce maximum de complexité correspond à la classe des automates intrinsèquement universels. Il est remarquable que l’on puisse représenter cette classe par un automate simple à six états. En choisissant différentes valeurs des paramètres d’un groupage rectangulaire, on reproduit à partir des orbites de cet automate intrinsèquement universel toutes les orbites de tous les automates cellulaires ! Pour se rendre compte de la performance, il nous faut préciser que parmi les automates reproduits se trouvent notamment tous les automates cellulaires dont les orbites sont parcourues par des particules animées d’une « vie propre » (un ordre local qui se propage) et les automates « Turing universels » (on désigne par ce terme des classes d’automates dont les orbites reproduisent tous les calculs possibles effectués par un ordinateur, comme le fait la machine de Turing). Nous montrons sur la figure à droite l’une des orbites d’un automate qui cumule ces formes de complexité structurelle et algorithmique : la règle 110 (01101110).

La règle 110 est un automate cellulaire « Turing universel » dont les diagrammes sont parcourus par des particules dotées d’une certaine indépendance.
Images : M. Delorme et J. Mazoyer

L’idée que la production d’une forme quelconque de complexité peut toujours se réduire à une somme de calculs, en d’autres termes au travail plus ou moins long d’un certain automate cellulaire « Turing universel », est assez répandue. Elle nous semble fausse comme nous l’avons déjà exprimé. La classification obtenue grâce au groupage rectangulaire fait apparaître une classe d’automates cellulaires « Turing universels » infiniment éloignée du maximum constitué des automates intrinsèquement universels. Le contraste entre la simplicité de l’automate intrinsèquement universel à six états et les formes extrêmes de complexité qu’il reproduit étonne. Comme on sait le construire, il n’apparaît que compliqué, il n’en demeure pas moins que certaines de ses orbites sont vraiment inextricables, ce qui le rend complexe !

Il est très surprenant que la simplicité des automates cellulaires les plus triviaux, et la complexité des automates capables de créer des « formes de vie » ou d’effectuer tous les calculs possibles, soient incluses dans une même structure.