MoGo, maître du jeu de Go ?

Jeu de Go au XVI^e siècle. Détail des « Quatre accomplissements ». Dans la Chine ancienne, le Go était en effet considéré comme l’un des quatre accomplissements de toute personne cultivée, à l’égal de la poésie, de la musique et de la peinture.
Source : Kano Eitoku / Wikipédia

Si tout le monde considère actuellement que les programmes joueurs d’échecs sont beaucoup plus forts que la plupart des humains, on ne peut pas en dire autant pour un jeu comme le Go. Les programmes joueurs de Go peinent à atteindre un niveau moyen, très loin des amateurs forts et encore plus des professionnels ! Pourquoi ? Deux raisons à cela : tout d’abord, il y a beaucoup plus de coups possibles au Go qu’aux échecs. Le jeu de Go se joue traditionnellement sur un plateau de jeu (goban en japonais) de 19 lignes et 19 colonnes, ce qui fait plus de 200 coups possibles dans une position typique, contre une quarantaine aux échecs. La combinatoire est donc beaucoup plus grande au Go. Ensuite, la taille de l’arbre des possibilités du jeu de Go est de l’ordre de 10¹⁷⁰ positions possibles (c’est-à-dire beaucoup plus grande que le nombre d’atomes dans l’univers) tandis que celle du jeu d’échecs n’est « que » de 10⁵⁰ environ.

Pour les informaticiens en général et les chercheurs — en modélisation statistique et en intelligence artificielle — en particulier, le jeu de Go est un problème très intéressant, qui soulève des problématiques difficiles dont les solutions pourraient s’appliquer dans d’autres domaines. C’est un défi de s’attaquer à un tel problème, d’autant plus que les techniques utilisées sont très proches de leurs domaines de recherche. Ainsi, ces travaux de recherche sont appliqués à un problème concret, difficile et ludique.

Le Go, un jeu plus complexe que les échecs

Né en Chine il y a plus de 4 000 ans et apparu depuis un millier d’années au Japon, le Go n’est arrivé que très récemment en Occident. Pour y jouer, on utilise un matériel très sommaire : un goban (plateau quadrillé) sur lequel on place des pierres noires et blanches. Il existe trois formats différents de gobans : le très populaire 19×19 intersections, le 13×13 (taille intermédiaire) et le 9×9 principalement utilisé pour les parties d’initiation. Les professionnels ne jouent qu’en 19×19, les autres tailles étant parfois choisies par les amateurs pour des parties plus rapides.

Au Go, on joue sur les intersections et non à l’intérieur des cases comme c’est le cas aux dames ou aux échecs. Deux joueurs s’affrontent, l’un aux pierres blanches, l’autre aux noires, le joueur aux pierres noires commençant toujours la partie. Une fois la première pierre (noire) posée, elle ne bouge plus. C’est ensuite au tour de l’adversaire de jouer. Le but du jeu ? Se constituer des territoires — un territoire, c’est le nombre d’intersections entourées de pierres de la même couleur — en prenant les pierres de l’adversaire.

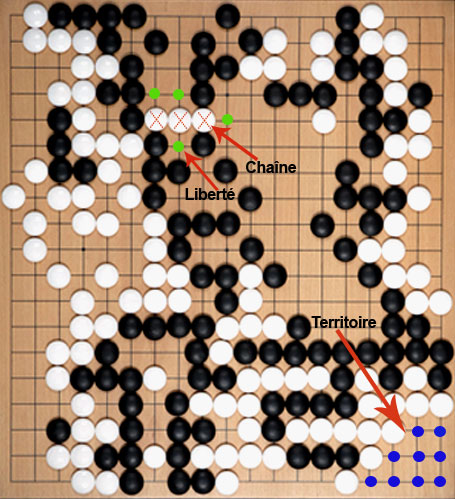
Partie de Go sur un goban de 19×19 intersections. Les pierres blanches marquées par des croix rouges (vers le haut du goban) sont voisines de proche en proche. Elles constituent une chaîne qui a quatre libertés (intersections marquées par des cercles verts). Sur le plateau, on a également délimité un territoire blanc (cercles bleus, en bas du goban), c’est-à-dire un groupe d’intersections entourées par des pierres de la même couleur.
Source : © INRIA / Photo : Christian Tourniaire

Pour gagner, un joueur doit dominer plus d’intersections que son adversaire en constituant des chaînes, c’est-à-dire en connectant ses propres pierres et en capturant des pierres adverses. Et attention, les diagonales ne comptent pas au Go ! Une chaîne reste sur le plateau de jeu tant qu’elle a au moins une liberté. On appelle liberté le nombre d’intersections vides autour d’une chaîne. À partir du moment où une chaîne n’a plus aucune liberté, le joueur concerné récupère les pierres. La partie se déroule alors jusqu’à ce que les deux joueurs passent leur tour. De plus, le ko simple interdit de jouer un coup tel que la position après capture serait exactement identique à la position précédente. Très importante, cette règle permet d’éviter de faire des parties infinies. À la fin, on compte le nombre de territoires possédés par chaque joueur et celui ayant le plus de territoires remporte la partie. Chaque intersection du territoire d’un joueur lui rapporte un point, ainsi que chacune de ses pierres encore présentes sur le goban. En outre, comme le joueur aux pierres noires commence toujours la partie, on considère que ce dernier a un avantage. Dans une partie à égalité, on attribue alors quelques points d’avance à son adversaire. C’est ce qu’on appelle le komi. Vous avez là 80% des règles du Go. Le reste, ce sont des règles qui diffèrent selon les pays, notamment pour le décompte exact du score.

Par ailleurs, les joueurs sont classés selon différents niveaux : ils s’échelonnent de 30^e Kyū (débutant) à 1^er Kyū, puis de 1^er dan à 9^e dan pour les joueurs amateurs. Les joueurs professionnels sont classés de 1^er à 9^e dan. Un niveau de 1^er dan professionnel correspond environ à un niveau de 7^e dan amateur. Entre amateurs, un niveau d’écart correspond à peu près à une pierre de handicap (pierre d’avance accordée au joueur le plus faible) alors qu’entre joueurs professionnels, c’est environ trois niveaux d’écart qui correspondent à une pierre de handicap.

Quand les joueurs s’affrontent…

Source : © INRIA / Photo : Jonathan Dumont

Plusieurs compétitions permettent de mesurer les forces relatives des programmes joueurs de Go. Deux outils sont principalement utilisés pour se comparer aux autres programmes : le Computer Go Server et le Kiseido Go Server (KGS).

Le Computer Go Server est un serveur sur Internet à partir duquel les programmes peuvent se connecter à n’importe quel moment, 24h/24 et 7 jours/7. Les programmes y jouent entre eux et on leur attribue un Elo au bout de plusieurs jours de parties. Très connu aux échecs, le Elo est utilisé pour classer les joueurs : ce chiffre permet de savoir la probabilité de gagner d’un joueur sur un autre. Un exemple : si un joueur a un Elo 2000 et un autre un Elo 1800, on va simplement calculer la différence de Elo entre les deux joueurs puis en déduire la probabilité de gagner du premier sur le second. Plus la différence de Elo est grande, plus la probabilité de gagner est forte. Par la suite, on applique une formule qui, à partir des victoires de chacun — par exemple, X a joué contre Y dix fois et a gagné cinq fois, Z a joué contre Y etc. —, permet de calculer le Elo de chacun. Le Elo détermine donc la force du joueur.

Sur le Computer Go Server, les parties se font sur des gobans de 9×9, les parties en 19×19 prenant beaucoup trop de temps, même pour faire jouer les programmes ! Faire un programme en 9×9 permet donc de le tester plus vite. De plus, les programmes étant assez faibles, ils sont meilleurs sur des petites tailles. Il est intéressant de développer les programmes sur des petites tailles afin de suivre leur progression, voir leurs forces ou faiblesses ainsi que leur niveau par rapport aux humains, d’autant plus que le nombre illimité de parties sur le Computer Go Server permet une évaluation plus précise des programmes.

Quant au KGS (Kiseido Go Server), c’est un serveur très populaire sur lequel des milliers d’humains se connectent et jouent. Tous les premiers week-ends du mois, un tournoi est organisé entre ordinateurs et dans les différentes tailles de goban. Sur KGS, le nombre de parties est fixe — entre 6 et 10 en moyenne — et au bout de ces parties, le joueur qui a gagné le plus souvent remporte le tournoi. Par ailleurs, l’évaluation des programmes est plus précise sur le Computer Go Server que sur le KGS. Sur un tournoi, le facteur chance est non négligeable : même le meilleur peut perdre parce qu’il n’a pas eu de chance. Mais c’est aussi ce qui fait le charme des tournois, le spectacle étant alors au rendez-vous. Les humains, professionnels ou amateurs, peuvent également affronter les programmes joueurs de Go dans une salle spéciale.

Certains joueurs se sont d’ailleurs mesurés à MoGo, le programme développé par le projet TAO (Thème Apprentissage et Optimisation) de l’INRIA Futurs et l’École Polytechnique. Les techniques utilisées par MoGo sont inspirées de la stratégie de Crazystone, un autre programme joueur de Go développé par Rémi Coulom, à Lille (projet SEQUEL, Inria Futurs). L’été dernier, aux Olympiades informatiques, Crazystone remportait la médaille d’or en 9×9 quand MoGo n’en était encore qu’à sa phase de conception !

Il est possible de jouer contre le programme MoGo à n’importe quel moment et à partir de n’importe quelle interface sur le serveur KGS. MoGo est actuellement 1^er parmi 142 programmes sur le Computer Go Server depuis août 2006. Il est arrivé en tête devant tous les programmes l’été dernier, à 1920 Elo, sachant qu’une large population de programmes se situent autour de 1900 Elo. Depuis, l’écart (en Elo) n’a cessé d’augmenter avec les autres programmes : MoGo est aujourd’hui à 2323 Elo, suivi de Valkyria (un programme plus jeune) à 2000 Elo. Pour vous donner un ordre d’idée, cela correspond à peu près à une probabilité de victoire de plus de 80% pour MoGo contre Valkyria.

Un ordinateur peut-il battre un joueur humain ? De nombreux individus se sont posés cette question ces dernières années. En 1997, la shodan (1^re dan) professionnelle Janice Kim battait le programme HandTalk — champion du monde des programmes de Go de 1995 à 1997 — malgré un handicap de vingt-cinq pierres, suivie de Martin Müller en 1998, 6^e dan amateur, qui battait Many Faces of Go malgré un handicap de vingt-neuf pierres. Plus récemment, un joueur 2^e dan s’est proposé pour affronter MoGo en 9×9 et MoGo a gagné une partie sur deux. Depuis, on peut considérer que MoGo a atteint le niveau dan en 9×9. Un « événement » dans le monde des joueurs de Go ! En effet, toutes les compétitions montrent que MoGo est assez bon, mais aucune compétition officielle ne permet d’évaluer le niveau pratique des programmes contre les humains.

Des principes communs à la plupart des jeux

Source : © INRIA / Photo : Christian Tourniaire

Tous les programmes de jeux de stratégie combinatoires abstraits ont un même principe de fonctionnement. Le programmeur construit un arbre qui correspond à une analyse des séquences de coups. Dans son arbre, chaque nœud représente une position du jeu. Ensuite, chaque fils va correspondre à une position atteignable de la racine (nœud ne possédant pas de parent). L’arbre va donc symboliser toutes les positions possibles et tous les moyens d’atteindre ces positions.

En explorant tout l’arbre des coups possibles, on pourrait trouver le meilleur coup, au sens où en jouant ce coup, l’adversaire n’aurait aucun moyen de nous empêcher de gagner, quel que soit ce qu’il joue. On peut ainsi calculer toutes nos réponses jusqu’à la fin du jeu et trouver le meilleur coup possible. C’est ce qu’on appelle la stratégie min-max (ou minimax). Pourquoi min-max ? Tout simplement parce que le joueur X cherche à jouer le meilleur coup, mais son adversaire Y veut l’empêcher de jouer le meilleur coup. Y joue donc le pire coup pour X. Ainsi on peut dire que X joue max tandis que son adversaire Y joue min. Voilà l’objectif à atteindre. C’est un optimal dans un certain sens mais ce n’est pas forcément la meilleure stratégie.

Imaginez que vous ayez une position perdante : si votre adversaire est extrêmement fort, il pourra toujours gagner mais s’il est de niveau « moyen », en jouant min-max, vous risquez de perdre car les réponses à vos coups peuvent être simples à trouver. Vous pouvez plutôt essayer de complexifier la situation en tendant des pièges à votre adversaire, et espérer ainsi renverser la situation pour gagner. Avec MoGo et la plupart des programmes de Go, on tente toujours d’approcher ce fameux min-max. C’est une stratégie idéale contre un joueur idéal. Dans un jeu comme le poker, il est important d’arriver à prévoir ce que va faire votre adversaire, à le « modéliser » mais dans les jeux comme le Go, les dames ou l’Othello, on cherche simplement à jouer le mieux possible contre un adversaire idéal. Un algorithme simple permet en théorie de trouver la meilleure stratégie : il suffit de construire tout l’arbre des possibilités. Mais cet arbre étant immense, il est totalement impossible de le visiter entièrement, ce qui montre bien qu’il faut avoir des techniques intelligentes pour réussir à s’en sortir. Toutes ces techniques — issues pour la plupart de travaux de recherche en intelligence artificielle — ont un point commun : elles n’essaient pas d’explorer toutes les possibilités mais uniquement de se focaliser sur un coup et d’éliminer les autres.

Des atouts comme UCT, un algorithme pour la recherche arborescente…

L’algorithme alpha-bêta est considéré comme la référence dans le domaine des jeux combinatoires. Couramment utilisé et très efficace notamment dans les échecs, cet algorithme « dit » : commençons par explorer certains coups puis quand on explore un autre coup, s’il est évident qu’il est moins bien que le premier, on arrête… On fait donc ce qu’on appelle des coupes : on réduit ainsi le facteur de branchement, c’est-à-dire le nombre de fils. Cependant, cet algorithme n’a pas fait ses preuves au Go et notre équipe a préféré utiliser l’algorithme UCT (Upper bound Confidence for Tree), publié en 2006. MoGo est le premier programme à avoir utilisé UCT.

UCT est basé sur un algorithme appelé UCB (Upper Confidence Bounds), inspiré par le problème des bandits-manchots.

UCT est tout simplement l’application d’UCB à un arbre et il a été développé récemment pour la recherche de solution minimax dans des arbres de dimensions gigantesques. En fait, il s’agit d’explorer l’arbre, mais surtout d’explorer plus souvent le meilleur coup !

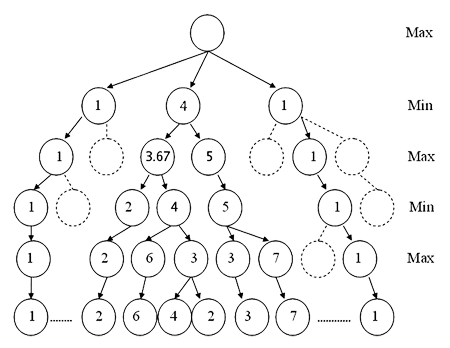
Exemple d’arbre exploré par l’algorithme UCT. Les nœuds (correspondants aux positions) dont les valeurs sont les plus prometteuses sont explorés en priorité. Chaque branche correspond à une succession de coups, et on modélise l’adversaire par un « étage min », signifiant que l’adversaire va tout faire pour contrer notre coup. L’algorithme UCT va explorer l’arbre de façon asymétrique, bien plus profondément (plus de coups prévus) pour les branches les plus intéressantes.
Image : Y. Wang et S. Gelly

On part alors de la racine (position courante) et à chaque étage, le problème équivaut un peu au problème des bandits : quel coup choisir ? On applique l’algorithme UCT jusqu’à ce qu’on atteigne une feuille, c’est-à-dire un coup (correspondant à une position) jamais vu et à ce moment là, on utilise une fonction d’évaluation qui nous indique le meilleur coup. Simples à mettre en œuvre, ces algorithmes ne demandent que très peu de lignes de programme. On explore peu à peu tous les coups de manière uniforme et lorsqu’un coup va nous sembler meilleur, on l’explore prioritairement et de plus en plus souvent. Au contraire de l’algorithme alpha-bêta, UCT visite plusieurs fois le même nœud (la même position, par le même chemin). À chaque nouvelle visite, l’algorithme peut soit choisir des suites de coups différentes, soit visiter l’arbre plus profondément, c’est-à-dire qu’on va le plus loin possible dans le développement du jeu. Ce comportement — explorer plusieurs fois la même position — implique cependant que dans le pire des cas, si on veut visiter toutes les positions jusqu’à une profondeur donnée, l’algorithme sera alors beaucoup moins efficace qu’alpha-bêta. Imaginez deux coups qui se détachent : ces coups vont être explorés beaucoup plus souvent et les mauvais coups beaucoup moins. Toutes les ressources de calcul vont donc être centrées sur la détermination du meilleur des deux coups.

Le fait intéressant est qu’on obtienne un algorithme très simple à la fin, efficace et facile à utiliser ! UCT n’est pas meilleur que l’algorithme alpha-bêta mais dans notre application, ses avantages sont multiples.

…et Monte-Carlo, une méthode de simulation statistique

Lorsqu’on est à une feuille de l’arbre (c’est-à-dire qu’il n’y a pas de fils), on a une position qu’il faut pouvoir évaluer. C’est la raison pour laquelle on a besoin d’une fonction d’évaluation. Tous les programmes de jeux utilisent une fonction d’évaluation, quel que soit le jeu.

Dans le jeu de Go, à un instant t, il est presque impossible de déterminer l’avance d’un joueur sur son adversaire, contrairement aux échecs où l’on arrive à faire des fonctions d’évaluation efficaces, c’est-à-dire qui arrivent à bien noter la position. La difficulté du Go vient non seulement de la multiplicité du nombre de coups possibles mais aussi de la fonction d’évaluation qui est mauvaise. Lorsqu’on a une bonne fonction d’évaluation, l’algorithme alpha-bêta est peut-être plus performant qu’UCT mais il est difficile d’être catégorique sur ce point dans la mesure où il n’y a pas eu d’expérience précise là-dessus.

En fait, on considère deux grandes approches dans la fonction d’évaluation : la méthode classique (pour les programmes moins récents) et Monte-Carlo. Les programmes développés depuis longtemps (plus de dix ans) se basent sur l’expertise humaine, c’est-à-dire qu’on prend des joueurs expérimentés qui vont essayer d’introduire leurs connaissances du jeu dans le programme : par exemple, dans telle position, il ne faut jamais jouer tel coup parce qu’on perd à coup sûr ; si on joue au centre, c’est bien, si on joue à côté, c’est moins bien, etc. Ils donnent donc un certain nombre de règles à la fois sur la fonction d’évaluation et sur les coups possibles.

Cette approche a fonctionné dans beaucoup de jeux comme les échecs : on a pu déterminer des caractéristiques des positions, la valeur des pièces, les positions, etc. Elle ne marche pas si mal que ça dans le Go car dans les grandes tailles de goban, c’est encore l’approche la plus efficace. D’ailleurs, les programmes les plus forts l’utilisent encore. Cependant, ce n’est pas une approche en laquelle notre équipe croyait car elle nécessite un temps humain considérable : il faut rencontrer beaucoup d’experts, pendant plusieurs années, pour qu’ils écrivent leurs petites règles, ce qui devient très vite compliqué. En outre, cette approche a montré ses limites : les programmes classiques restent toujours très faibles par rapport aux humains et leur progression est en plus assez lente. Comparativement, MoGo par exemple, a aujourd’hui un niveau totalement incomparable avec celui qu’il avait il y a six mois. Le choix d’utiliser Monte-Carlo n’est donc pas incohérent…

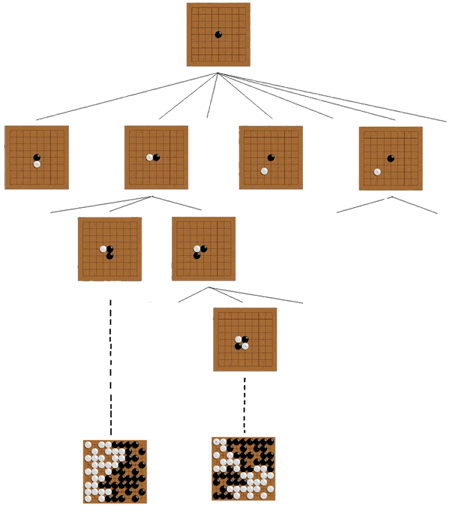
Illustration de l’algorithme UCT dans le Go en utilisant Monte-Carlo comme fonction d’évaluation. Chaque nœud de l’arbre des possibilités représente une position de Go et chaque arc permet de passer d’une position à une autre en jouant un coup. On part de la racine (en haut, qui correspond à la position courante) et on descend dans l’arbre à chaque étage suivant le coup qui semble le plus prometteur (optimiste dans l’incertain). Une fois une feuille atteinte, on joue une partie aléatoire jusqu’à la fin (en pointillé sur la figure) pour évaluer la position. On remonte ensuite la valeur obtenue (victoire ou défaite à la fin de la simulation) dans tous les nœuds visités. Après chaque simulation, on ajoute un nœud pour agrandir l’arbre.
Image : Y. Wang et S. Gelly

L’idée de Monte-Carlo est de prendre une position et de simplement jouer au hasard des pierres noires et blanches sur le goban, jusqu’à ce qu’on remplisse tout le plateau sauf les yeux (ensembles de pierres qui entourent une liberté pour protéger la chaîne). Si on met cette définition de l’œil dans le programme et qu’après, il joue au hasard, il va finir par remplir tout le goban. Ensuite, on compte les points. Monte-Carlo dit : « pour évaluer une position, finissons la partie. » On fait donc une simulation de partie. Une fois la partie terminée, des règles précises nous indiquent comment compter le score. Monte-Carlo simule des parties, prend la moyenne de ces simulations, et est capable de donner un score à la position, ce qui nous donne une fonction d’évaluation de la position.

Tout le principe de MoGo tient dans cette subtile association entre l’algorithme UCT et la fonction d’évaluation Monte-Carlo. Dans l’arbre, chaque nœud correspond à une position. Imaginez une certaine position de départ : MoGo crée un arbre itérativement et à chaque itération, il va ajouter un nœud. Il visite donc son arbre et va jusqu’à une feuille. Une fois qu’il a atteint une feuille, il lance une simulation de Monte-Carlo et ajoute un nœud (une nouvelle position). Ainsi, l’arbre va grossir de façon asymétrique, c’est-à-dire qu’il va visiter plus souvent les meilleurs coups (c’est le principe d’UCT) et les explorer en priorité. Ensuite, lorsqu’il est temps pour lui de jouer, MoGo joue le meilleur coup qu’il a vu jusque-là.

Pourquoi MoGo est-il champion ?

Deux raisons au succès de MoGo : d’abord l’algorithme UCT est très performant. De plus en plus de programmes l’utilisent, Valkyria notamment. Ensuite, la fonction d’évaluation Monte-Carlo est efficace car elle permet de dire d’une position si elle est gagnante ou perdante.

Les premières versions de programmes de Monte-Carlo étaient uniformes c’est-à-dire que pour finir la partie, le simulateur remplissait uniformément le goban. Il jouait au hasard uniformément parmi tous les coups, sans en préférer aucun. On parle de coups aléatoires simples. Ensuite, des informaticiens ont essayé d’améliorer Monte-Carlo pour le Go. L’idée générale était de toujours essayer de faire les meilleurs coups. Or, en jouant uniformément, on fait quand même pas mal de mauvais coups. C’est pourquoi nous avons choisi de biaiser cette distribution vers les bons coups.

Notre but n’est pas de faire plus de meilleurs coups mais de réussir à bien évaluer les positions, de faire des suites de parties crédibles pour un joueur de Go. En fait, nous avons essayé d’introduire des séquences de coups forcés. L’idée, c’est de donner des positions locales représentatives (types) dans les simulations aléatoires et de forcer ce genre de coups. On identifie alors ce qu’on a appelé des motifs. Ce sont des positions types en 3×3.

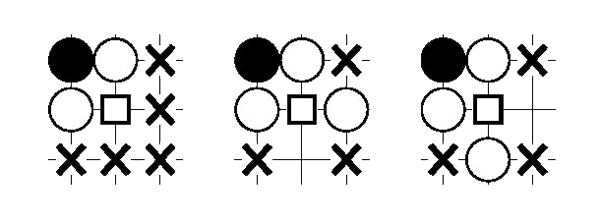
Le carré blanc correspond à une position, et la question est de savoir s’il est intéressant de jouer dans la configuration donnée. Le principe est de donner des positions locales représentatives (types) et de forcer ce genre de coups. On recherche seulement ces positions locales représentatives autour du dernier coup joué. Si le motif correspond, on joue sur l’intersection marquée par un carré blanc, sinon on joue de manière aléatoire ailleurs. Sur le schéma, un rond noir ou blanc correspond à une pierre noire ou blanche et une intersection vide à une absence de pierre. Une croix signifie que l’on ne considère pas ce qu’il y a sur cette intersection (qu’il y ait une pierre ou pas). Quand on lance la simulation de Monte-Carlo, noir par exemple, joue quelque part ; on regarde ensuite autour de ce dernier coup les positions possibles pour voir si cela correspond à un motif. Si on trouve une correspondance avec un motif, on pose une pierre blanche à côté. Ainsi, des séquences de coups consécutifs vont se dégager et l’évaluation sera beaucoup plus précise.
Image : Y. Wang et S. Gelly

Cela ressemble un peu à l’idée des travaux précédents qui essayaient de biaiser les coups pour faire des meilleurs coups sauf que nous ne biaisons pas des coups mais des séquences de coups (ou succession de coups). On force des coups mais en forçant également les coups voisins, on crée des séquences de coups. Nos expériences confirment qu’il vaut mieux créer des séquences de coups localement comme on le fait dans MoGo grâce aux motifs. Si au lieu de chercher les bons coups de manière localisée, on les cherche sur tout le goban, les évaluations sont moins bonnes. C’est une subtilité un peu étrange — logiquement, si on cherche les bons coups partout, cela vaut mieux que sur un côté — mais c’est ce qui a fait la grande force de MoGo.

Aujourd’hui, presque tous les programmes performants en 9×9 utilisent à la fois l’algorithme UCT et Monte-Carlo. La supériorité de MoGo doit être attribuée à notre fonction d’évaluation et à nos améliorations des séquences. Donner des bonnes séquences, donne de meilleures fonctions d’évaluations. De plus, on a modifié quelques détails dans l’algorithme UCT et ces améliorations nous procurent aussi un certain avantage.

Et l’avenir ?

MoGo est aujourd’hui l’un des meilleurs joueurs artificiels de Go mais il doit encore progresser en 9×9 pour battre des humains très forts dans ce format, comme les joueurs professionnels. C’est motivant d’avoir atteint un bon niveau car on attire plus d’intérêt de la part des joueurs et du grand public. On est encore loin du Kasparov contre Deeper blue, mais on progresse… Bientôt peut-être, on pourra battre les humains vraiment forts en 9×9. En décembre dernier, MoGo a participé à un tournoi lent de KGS (une partie de 12h par côté). L’intérêt était de voir comment, dans le futur, les programmes passeront à l’échelle, c’est-à-dire, si on leur donne plus de puissance de calcul, qu’est-ce qui se passera ? Et MoGo a gagné ce tournoi en 19×19 alors qu’il n’a pas encore un bon niveau dans ce format de jeu. Cela montre bien qu’avec le temps, il devient plus fort et sa progression en terme de puissance de calcul est meilleure que celle d’autres programmes.

En fait, le niveau de MoGo s’améliore avec le temps de réflexion sur une position donnée. Il commence chaque réflexion sur un coup de zéro, c’est-à-dire qu’il ne généralise pas les connaissances qu’il a acquises sur une partie précédente pour mieux évaluer un coup donné. Une partie de l’arbre peut cependant être utilisée d’un coup sur l’autre dans la même partie. Pouvoir généraliser les connaissances d’une partie sur l’autre est un défi intéressant, mais avec peu de succès pour le moment. C’est l’une des perspectives d’évolution des programmes joueurs de Go…

Par ailleurs, nous avons terminé deuxième du tournoi normal KGS (en 30 min). Et maintenant, MoGo est au niveau des meilleurs programmes qui participent aux tournois en 19×19. Il y a évidemment une inconnue sur les programmes absents des tournois, comme les programmes commerciaux. Mais pour le futur, on espère quand même progresser en 9×9 à cause de l’intérêt humain fort, et en 19×19 parce que c’est dans cette taille que se trouve l’essence même du jeu de Go !

Beaucoup de gens sont pessimistes quant à l’évolution des programmes joueurs de Go mais nous restons optimistes. Jusqu’à présent, du peu que nous avons déjà vu de l’efficacité de l’approche par Monte-Carlo et UCT dans MoGo, mais également dans d’autres programmes, on peut espérer que les progrès soient encore rapides. Il reste de nombreuses améliorations à faire dans cette voie et il y a un bon espoir pour que les programmes de Go rattrapent les humains assez vite, au moins pour le 9×9 et le 13×13. En 9×9 par exemple, seuls des humains expérimentés réussissent à battre les meilleurs programmes, même si on est encore loin du niveau des professionnels. En 19×19, cela prendra certainement plus de temps, mais ce n’est qu’une question d’années. Les humains ont toujours été très fiers. Aux échecs par exemple, on disait à l’époque que l’homme ne serait jamais battu par une machine et pourtant, c’est arrivé ! Dans le Go, tout reste encore à prouver mais pourquoi pas ? Soyons optimistes !

Quelques liens vous sont proposés pour en savoir plus sur le Go et les programmes joueurs de Go.