Les longues traînes

La notion de moyenne semble facile, d’une difficulté au-dessous de la moyenne… Détrompez-vous, elle est fertile en chausse-trape : voyez le clin d’œil illustré ci-dessous. Et il y a plus grave que les problèmes créés par les propriétés de la moyenne, il y a un problème d’existence : il arrive, comme dans les répartitions à longue traîne, que les moyennes disparaissent.

Diminution simultanée des moyennes !
Dans la rue Gödel, l’âge des cinq habitants est 8, 14, 20, 23 et 35 ans, l’âge moyen étant de 20 ans. Dans la rue Turing, l’âge des six habitants est 25, 30, 35, 40, 45 et 59 ans, soit en moyenne 39 ans.
Jacques, de la rue Gödel, qui a 35 ans, va habiter la rue Turing : l’âge moyen dans la rue Gödel est maintenant de (8 + 14 + 20 + 23) / 4 = 16,25 ans et l’âge moyen dans la rue Turing (25 + 30 + 35 + 35 + 40 + 45 + 59) / 7 = 38,42 ans. Les moyennes des âges dans les deux rues ont toutes deux diminué !
La règle est paradoxale mais simple : quand un habitant de la rue Gödel passe rue Turing, si son âge est supérieur à l’âge moyen des habitants de la rue Gödel et inférieur à l’âge moyen des habitants de la rue Turing, alors l’âge moyen baisse dans les deux rues !
Dessin J.-M. Thiriet © Pour la Science.

Une manière de mesurer plus précisément les moyennes consiste, nous disent les statistiques classiques, à agrandir la taille de l’échantillon pris en compte : nous réduisons ainsi la part des aléas. Rien n’est plus faux pour les répartitions à longue traîne rencontrées dans un grand nombre de phénomènes naturels, certains ayant une importance économique notable.

Examinons, en suivant Brian Hayes (voir la bibliographie en fin d’article), deux algorithmes S(n) et P(n) qui illustrent le phénomène.
1) S(n) : l’algorithme (ou tout autre moyen avec des dés ou des cartes) tire au hasard des entiers entre 1 et n, jusqu’à rencontrer un 1 ; il additionne alors tous les nombres obtenus.
2) P(n) : l’algorithme tire au hasard des entiers entre 1 et n, jusqu’à tirer un 1 ; il multiplie alors tous les nombres obtenus.

Détaillons le cas n égal à 5 : l’algorithme tire au hasard des nombres compris entre 1 et 5 jusqu’à obtenir un 1. Cela donne : 3, 4, 2, 2, 4, 5, 1. La somme des nombres tirés est alors S(5) = 3 + 4 + 2 + 2 + 4 + 5 + 1 = 21. Le produit est P(5) = 3 x 4 x 2 x 2 x 4 x 5 x 1 = 960.

En utilisant plusieurs fois les algorithmes S(5) et P(5) nous obtenons des nombres assez différents car les suites qui interviennent sont plus ou moins longues avant que nous tombions sur le 1 qui fixe l’arrêt. Pour S(5) calculé vingt fois de suite, nous aurons par exemple : 36, 7, 6, 21, 1, 8, 13, 51, 22, 1, 28, 10, 8, 1, 37, 38, 11, 10, 23, 1. L’algorithme P(5) utilisé vingt fois donne : 4, 1, 2, 14 400, 4, 1, 48, 15, 1 500, 1, 3 000, 25, 5, 288, 8, 34 560 000, 64 800, 3, 1, 5 760.

Bien sûr les produits varient plus que les sommes. Regardons de plus près. Pour cela évaluons la moyenne des données que produisent les algorithmes S(5) et P(5). En faisant fonctionner S(5) cent fois de suite, et en calculant la moyenne arithmétique des résultats, nous trouvons M = 12,92 ; 1 000 calculs donnent M = 14,854 ; 10 000 calculs, M = 14,948 ; 100 000 calculs, M = 15,018 ; 1 000 000 calculs, M = 14,991.

Ces résultats sont de plus en plus proches de 15. Ce n’est pas un hasard, car le raisonnement qui va suivre montre qu’effectivement la moyenne arithmétique des nombres fournis par l’algorithme S(5) est 15. Pour un entier n fixé, d’une part, on établit par un calcul de série que la longueur moyenne d’une suite de tirages (chaque suite donnant une somme) est n ; d’autre part la moyenne d’un nombre tiré au hasard entre 1 et n vaut (n + 1) / 2 car la somme 1 + 2 + … + n vaut n (n + 1) / 2. La valeur moyenne des nombres produits par S(n) vaut donc n (n + 1) / 2. Pour n = 5 cela fait 15, ce que l’expérimentation numérique avait découvert.

Une moyenne rebelle

Pour P(5), l’algorithme du produit, les résultats expérimentaux sont très différents et plutôt étranges. Une moyenne arithmétique sur 100 calculs donne 6,841 . 10⁶, sur 1 000 calculs 1,819 . 10¹³, sur 10 000 calculs 1,858 . 10²⁰, sur 100 000 calculs 5,982 . 10²¹, sur 1 000 000 calculs, 1,709 . 10²⁵.

La moyenne des produits des nombres obtenus dans chaque série ne semble pas stable et plus longue est la série de nombres produits par P(5), plus la moyenne obtenue est grande. Prendre une longue série de données n’améliore pas l’évaluation de la moyenne : la moyenne a disparu !

L’explication demande un peu d’attention. Pour mener le raisonnement, nous commençons par considérer le cas n = 2 qui fournira la clef de tous les autres cas. L’algorithme P(2) engendre avec la même probabilité des 1 et des 2, jusqu’à ce qu’il tire un 1 ; le nombre donné par P(2) est alors le produit de tous les 2 obtenus avant le 1. Nous en déduisons qu’avec la probabilité 1/2, la série s’arrête immédiatement, série [1] dont le produit est 1. Avec une probabilité 1/4 la série est [2, 1] dont le produit est 2. Avec une probabilité 1/8 la série est [2, 2, 1] et le produit est 4. Avec une probabilité 1/16 la série est [2, 2, 2, 1] et le produit est 8, etc.

La moyenne des nombres engendrés par P(2) pondérée par les probabilités de les obtenir (on parle parfois d’espérance mathématique pour ce type de moyenne) doit nous indiquer ce que nous obtiendrions en moyenne en faisant fonctionner l’algorithme P(2) un très grand nombre de fois. Cette moyenne pondérée est (1/2) x 1 + (1/4) x 2 + (1/8) x 4 + (1/16) x 8 + … = 1/2 + 1/2 + 1/2 + … = ∞ : la moyenne pondérée pour P(2) est infinie !

Ce qui se passe pour P(n) lorsque n est plus grand que 2 est encore pire. D’une part, les nombres tirés sont plus grands et, d’autre part, les séries de nombres que P(n) tire avant d’en faire le produit sont plus longues. La « moyenne » des valeurs produites par P(n) (pour tout n fixé) est donc elle aussi infinie. Plus vous prenez de nombres pour évaluer la moyenne arithmétique des P(n), plus le résultat obtenu est grand. C’est vrai pour P(2), pour P(5) et pour tout P(n).

Ce que nous avons constaté en voulant calculer les moyennes des valeurs données par P(5) s’explique donc parfaitement. La moyenne a une valeur infinie, et donc plus nous essayons de l’évaluer plus nous obtenons de grands résultats, sans que jamais bien sûr ne cesse l’augmentation. La figure ci-dessous illustre que l’augmentation de la moyenne calculée croît exponentiellement en fonction du nombre de résultats que nous prenons en compte pour l’évaluer.

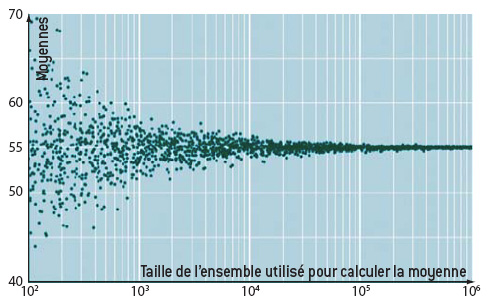
L’algorithme S(10) tire au hasard un nombre entier entre 1 et 10 jusqu’à ce que qu’il obtienne la valeur 1 et additionne les résultats des tirages.
Ces valeurs aléatoires s’étalent autour d’une valeur centrale, égale à 55. Plus le nombre de données utilisées pour effectuer le calcul de la moyenne est grand, plus cette moyenne est proche de 55. Les 2 000 points dessinés ici correspondent à 2 000 calculs de moyenne avec des effectifs augmentant de 100 à un million.

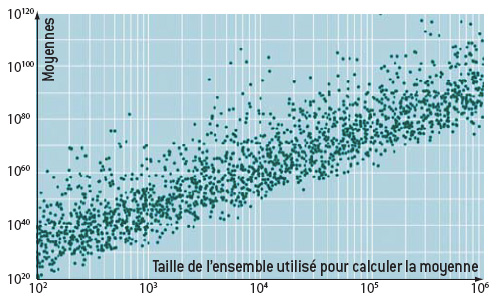
L’algorithme P(10) multiplie les résultats de tirages aléatoires avec les mêmes règles que S(10).
Contrairement à ce qui se passe pour S(10), les nombres obtenus sont très éparpillés. Quand on en calcule la moyenne, on n’observe pas de convergence, même en augmentant le nombre de données prises en compte. En utilisant une échelle logarithmique sur l’axe des y et en représentant les résultats de 2 000 calculs de moyenne comme précédemment, on obtient un nuage de points qui s’élève en suivant approximativement une droite. Cela signifie, non seulement qu’il n’y aura jamais convergence vers une valeur moyenne (la moyenne n’existe pas !), mais que, lorsque l’on prend un grand nombre de données, les résultats des calculs de moyennes se dispersent de manière exponentielle.
Les calculs des figures ci-dessus ont été réalisés par Bryan Hayes.
Infographie © Pour la Science.

Rare, mais jamais négligeable

Ainsi les nombres engendrés par P(2) (ou P(5), ou P(n) pour n’importe quel n fixé) sont rarement très grands, mais la valeur de ces grands nombres compense leur rareté et ils pèsent donc tous sur la moyenne. Comme ils sont une infinité à peser ainsi, la moyenne est infinie.

Notons la propriété amusante de la distribution de nombres donnée par l’algorithme P(n) : toutes les valeurs individuelles sont en dessous de la moyenne. Nous avons l’idée que les valeurs d’une série numérique se répartissent en dessous et au-dessus de la moyenne arithmétique, pas nécessairement de manière parfaitement égale, mais un peu de chaque côté quand même. Lorsqu’une moyenne est finie, cette idée est exacte : il est impossible que toutes les valeurs d’une série finie de nombres soient en dessous de leur moyenne arithmétique. Avec les distributions possédant une moyenne infinie, ce n’est plus impossible !

Précisons que les valeurs produites par l’algorithme P(n) ne sont pas sauvages en tout. En effet :
a) Elles possèdent une moyenne géométrique finie (la moyenne géométrique de n nombres est la racine n-ième de leur produit). Cette moyenne géométrique est n! (le produit des nombres de 1 à n) et on démontre que P(n) dépasse n! avec une probabilité qui est le nombre transcendant 1/e.
b) Elles ont une médiane finie. Par définition la médiane est telle qu’il y a autant de valeurs plus grandes que plus petites. Pour n égal à 10, c’est environ 27.

La distribution des valeurs données par P(n), n fixé, vous semble peut-être pathologique et tout juste bonne à amuser quelques mathématiciens en quête d’émotions et indifférents aux réalités du monde. Vous pensez que dans la nature on ne rencontrera jamais de distributions de données aussi absurdes car en pratique chaque série de données venant d’un processus naturel (taille des êtres humains, tailles des cratères de la lune, gravité des tremblements de terre, etc.), possède une moyenne et plus globalement présente une allure régulière. Détrompez-vous : les distributions du type P(n) sont fréquentes dans le monde réel.

Les statisticiens aiment bien la fameuse courbe en cloche ou loi normale (ou encore loi de Gauss) que l’on rencontre dans toutes sortes de circonstance. Elle possède cependant un défaut majeur : dès que l’on considère une valeur s’écartant sensiblement de la moyenne (qui là existe), la probabilité de tomber sur un objet correspondant à cette valeur devient petite, et même si petite qu’on doit vite la considérer comme négligeable.

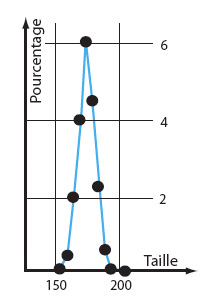
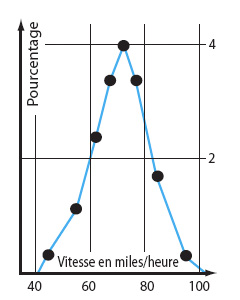
Courbes de la taille des Américains (à gauche) et de la vitesse des voitures sur une autoroute (à droite). Ces courbes sont très regroupées autour des valeurs centrales. On considère que ce sont approximativement des lois normales. Cela signifie en particulier une très rapide décroissance de la courbe dès qu’on s’éloigne des valeurs les plus fréquentes. Infographie © Pour la Science.

La distribution des tailles des adultes humains se répartit autour de 1,75 mètre et très peu d’humains adultes se trouvent hors de l’intervalle 1,50 – 2 mètres, aucun hors de l’intervalle 0,5 – 3 mètres. La répartition des tailles humaines suit en gros une loi normale et c’est pour cela qu’aucune valeur ne s’éloigne des valeurs les plus fréquentes.

Loi de Gauss ou longue traîne ?

Or, on a remarqué depuis longtemps que certaines distributions naturelles n’avaient pas cette propriété de décroissance. Le sociologue et économiste Vilfredo Pareto (1848-1923) a noté, il y a déjà un siècle, que les revenus des gens s’étalent bien loin au-delà des nombres les plus fréquents. On nomme distribution de Pareto une distribution de probabilités telle que « la probabilité pour que N dépasse x est supérieure à x ^– a » (le nombre a est un paramètre positif). Cette inégalité, valable pour les revenus des gens jusqu’au revenu de l’homme le plus riche (Bill Gates en 2006), a pour conséquence que même si on considère une très grande valeur pour x, la proportion de gens dont le revenu dépasse x reste non négligeable. Le revenu des gens suit une loi de Pareto et pas une loi normale, (si c’était le cas personne ne gagnerait 100 000 euros par mois).

Les lois de Pareto sont parfois qualifiées de lois à « queue épaisse » car la partie de la courbe correspondant aux grandes valeurs de N (la queue de la courbe) tend vers zéro en restant assez épaisse comparée à ce qui se passe pour la loi normale dont la queue décroît exponentiellement vite. Plus récemment on a aussi utilisé l’expression plus élégante de « loi à longue traîne ». Les termes de « loi de Zipf », « loi de puissance » ou « loi à invariance d’échelle » désignent des concepts presque équivalents, mais nous n’entrerons pas dans ces subtilités mathématiques et utiliserons les termes de loi de Pareto et loi à longue traîne.

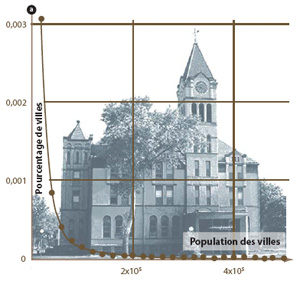
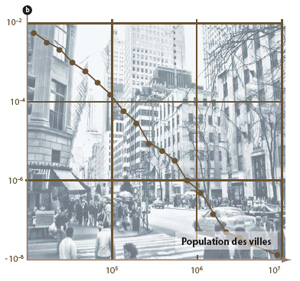
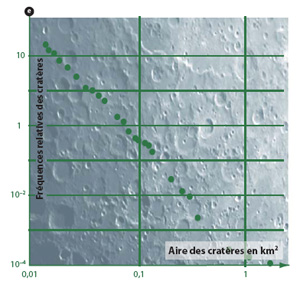
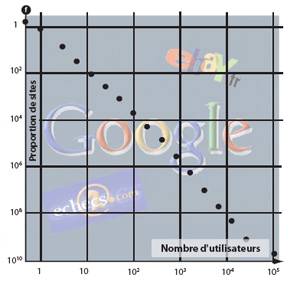
Les « longues traînes » apparaissent quand il y a plus de cas extrêmes que n’en prévoit la loi classique des statistiques, la loi en cloche de Gauss. Ainsi (a) représente la proportion, en fonction de leur population, des villes américaines de plus de 10 000 habitants. Le fait que les données, en coordonnées logarithmiques, se disposent le long d’une droite (b) signifie que la distribution, une « longue traîne », est une loi de puissance du type x–a (la loi de Gauss, en exp (–x2), donnerait une parabole et non une droite). Les exemples suivants sont d’autres cas de longues traînes : la fréquence en pourcentage des 250 noms de famille les plus courants (c), la fréquence d’apparition des mots dans Moby Dick, d’Herman Melville (d), la distribution des aires des cratères lunaires (e), la distribution du nombre d’utilisateurs par site (f). Infographie © Pour la Science.

Les lois à longue traîne se retrouvent dans un nombre étonnant de phénomènes naturels et artificiels. Citons : la taille des villes ; la force des tremblements de terre ; le diamètre des cratères à la surface de la lune ; la gravité des incendies de forêt ; le nombre d’espèces par genre dans la classification des mammifères. Mais aussi : la fréquence d’utilisation des mots (classés d’abord par fréquence d’utilisation décroissante) ; l’intensité des guerres (mesurée par le nombre de morts au combat) ; la répartition des noms de famille (classés du plus fréquent au moins fréquent) etc.

Depuis quelques années l’étude des réseaux informatiques, dont on observe la topologie, la croissance et le fonctionnement comme on observe des phénomènes physiques, a fait découvrir un nombre important de nouvelles lois à longue traîne. Citons : le nombre de liens pointant sur une page internet, la taille des fichiers qui circulent sur un réseau, le taux de fréquentation d’une page donnée, etc.

Notons que certaines de ces lois sont, comme P(n), sans moyenne, mais que ce n’est pas systématiquement le cas. Ce problème de moyenne absente (ou infinie pour les mathématiciens) n’a d’ailleurs qu’une importance relative quand on s’intéresse à des lois provenant du monde réel car à chaque instant on ne dispose bien sûr que d’un nombre fini de données dont rien ne nous empêche d’évaluer la moyenne.

Pour voir qu’une distribution de données suit une loi de Pareto, nous dessinons une représentation graphique de la distribution en utilisant des coordonnées logarithmiques : si nous avons affaire à une loi de Pareto, les données se regroupent selon une droite dont la pente permet de connaître le paramètre a. Le fait pour une loi ainsi représentée de donner une droite sur plusieurs ordres de grandeur est suffisant pour la classer dans la catégorie des lois de Pareto.

Pour expliquer les rencontres fréquentes avec de telles lois, toutes sortes d’idées ont été évoquées. L’une d’elles est directement reliée à notre algorithme P(n) : défendue récemment par William Reed et Barry Hughes, elle considère des processus à croissance exponentielle qui s’arrêtent brusquement. La multiplication entre eux de nombres pris au hasard dans un ensemble centré autour d’une valeur moyenne, arrêtée à un moment tiré lui aussi au hasard selon une méthode qui produit l’arrêt au bout d’un temps moyen fixé (P(n) est un processus multiplicatif de ce type), conduit à une loi de Pareto.

Ce que nous avions constaté expérimentalement n’était donc pas étonnant : tout processus du type de celui utilisé par P(n) conduit à une loi de Pareto. La croissance des villes, l’augmentation d’un revenu, la taille des fichiers manipulés en informatique sont le résultat de processus qu’on peut, au moins en première approximation, voir comme résultant d’une telle logique : quelque chose s’accroît multiplicativement (donc exponentiellement) pendant une durée qui ne peut qu’être limitée, et cela produit donc une distribution de valeurs de type loi de Pareto.

Le commerce électronique : faire fortune avec la longue traîne ?

Ces lois à longue traîne sont la clef des réussites du commerce électronique sur Internet, Amazon, Google, Ebay et quelques autres. C’est l’idée que défend Chris Anderson dans un livre récent La longue traîne. La nouvelle économie est là. Éditions Pearson Education France, Paris, 2007.

Penons l’exemple d’Amazon fondée par Jeff Bezos en 1994. Son objectif est de vendre des livres par le biais d’Internet sans imprimer de catalogues. Cette entreprise a atteint en 2006 un chiffre d’affaires de plus de 10 milliards de dollars et a réalisé, toujours en 2006, 190 millions de dollars de bénéfice. Le site Internet vend aujourd’hui d’autres produits que les livres (CD, DVD, appareils photographiques, etc.), mais c’est autour du commerce des livres que se sont construits sa réputation et son succès.

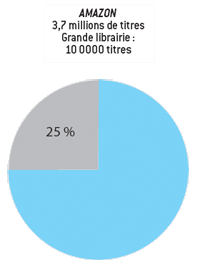
Aucune librairie ne pourra jamais concurrencer Amazon ou les entreprises équivalentes d’Internet. Les plus grosses librairies du monde proposent de l’ordre de 100 000 titres différents et jamais plus de 200 000, ce qui est énorme et exige d’immenses surfaces de ventes. Amazon en propose plus de trois millions. Plus important encore, un quart des ventes de livres porte sur des titres qui ne sont pas dans les 100 000 premiers du classement et donc sont absents des rayons d’une grande librairie. Contrairement à ce qu’on a longtemps pensé, les produits qui se vendent peu ne doivent pas être négligés, car pris ensemble, ils engendrent une part importante des chiffres d’affaires potentiels d’un secteur donné.

Les produits de fin de listes, de la longue traîne, ne pouvaient pas être pris en considération par le commerce traditionnel : il n’est pas rentable de stocker et d’exposer des articles qui restent trop longtemps dans les rayons. La longue traîne était donc négligée, sans que personne ne cherche à en évaluer le volume global.

Or les produits qui sont l’objet d’une faible demande, et qui individuellement ne constituent qu’une proportion insignifiante des ventes, représentent collectivement une part de marché, aussi importante que celle des best-sellers, à condition que le système de distri bution les propose. Comme dans de nombreux phénomènes sociaux informatiques et du monde naturel, la demande des consommateurs est largement étalée autour des valeurs les plus probables. Elle exhibe la fameuse longue traîne qui dès qu’elle peut se manifester change radicalement la répartition des ventes.

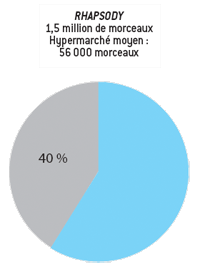
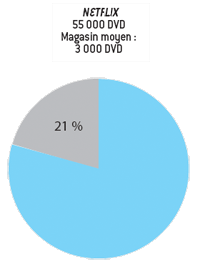
La longue traîne et Internet : une partie notable d’un secteur commercial provient de la longue traîne (les petites niches comportant peu de produits, chacun peu vendu). Rhapsody, magasin de vente en ligne de morceaux musicaux numérisés, réalise 40 pour cent de son chiffre d’affaires avec des morceaux non disponibles dans un magasin de musique traditionnel. Netflix réalise 21 pour cent de ses locations de DVD avec des produits absents des boutiques de quartier. Amazon obtient 25 pour cent de ses ventes avec des livres que les plus grandes librairies ne proposent pas. Données tirées du livre de C. Anderson, La longue traîne. La nouvelle économie est là. Infographie © Pour la Science.

Le phénomène avait été remarqué dans l’édition musicale où l’on a constaté depuis quinze ans une baisse de l’importance des plus gros succès comparés à ceux des années 1980. C’est, là encore, l’expression de la longue traîne, cette fois liée à la baisse des coûts d’enregistrement, de production et de duplication des CD : dès que le public le peut, il répartit ses achats sur des produits plus nombreux et se détourne relativement des produits phares correspondant aux grands succès.

Les petites niches devenues peu coûteuses à prendre en compte et à proposer deviennent des sources nouvelles de ventes tout en permettant souvent des profits supérieurs aux autres niches car elles sont moins sujettes à la concurrence.

Dans le commerce de la location de cassettes vidéos et de DVD, un magasin traditionnel est limité par la longueur des étagères où sont exposés les produits. Netflix, une entreprise américaine de location de DVD par correspondance, dispose d’entrepôts centralisés, qui engendrent des coûts de stockage très bas. Le coût de distribution étant le même pour un film populaire ou pas, la location reste rentable en ayant un catalogue bien plus large que celui des magasins traditionnels de quartier. Le système de stockage et de distribution permet ainsi de louer davantage de films et conduit Netflix à exploiter la longue traîne. Ainsi, le progrès technique conduit à un changement de structure du marché.

Les outils de stockage et de consultation de l’information sur les produits proposés ne sont limités par rien. Non seulement la description précise des produits est offerte, mais des compléments sous la forme de commentaires laissés par les consommateurs eux-mêmes sont proposés par Amazon, ainsi que des extraits des œuvres quand il s’agit de livres ou de morceaux musicaux. Parfois ce sont même les produits qui deviennent numériques ce qui entraîne une baisse encore plus importante des coûts de stockage et d’acheminement des produits vers les consommateurs (livres numériques, morceaux de musique, films).

Des outils de filtrages informatiques assistent le consommateur : à partir de quelques mots, le logiciel de recherche sélectionne les livres, CD, ou autres objets susceptibles d’être achetés et une multitude de fonctions aident l’acheteur à explorer l’ensemble de l’offre dont il ne visualise que la partie la plus susceptible de l’intéresser. Les outils de conseil jouent aussi un rôle important dans l’expression de la longue traîne : à partir du profil réalisé du consommateur résultant en particulier de ses achats passés, des articles sont suggérés, des email sont envoyés, etc.

Google et eBay aussi

Quand l’effet longue traîne devient visible et que la technologie permet de la prendre en compte, les goûts minoritaires sont mieux satisfaits et s’épanouissent, ce qui augmente encore la taille (son épaisseur et sa longueur) de la traîne. Le plus petit dénominateur commun n’est plus ce qui fixe la consommation de chacun, et les clients qui obtiennent une satisfaction accrue multiplient les achats.

À mesure que le concept de longue traîne est pris en considération, il engendre des changements qui concernent de plus en plus de secteurs de l’économie. Le commerce s’éloigne progressivement d’un marché qui privilégiait les têtes de gondoles. De nouveaux métiers apparaissent avec la mission de gérer la longue traîne : choisir les produits susceptibles de remplir des niches, aussi petites soient-elles ; perfectionner la recherche d’informations concernant la multitude toujours plus étendue des produits offerts ; parfaire la gestion des stocks et la marge unitaire ; organiser le plus adroitement possible l’information et la relance des clients sur des produits toujours plus variés.

La société Google, par le moyen des achats de mots, utilise la longue traîne de l’offre publicitaire. En réponse à une requête, des liens publicitaires ciblés apparaissent sur la partie droite (et en haut en grisé) de la page que Google affiche. Google est rémunéré en fonction du nombre de clics sur ces liens. Ce système permet la mise en place de campagnes publicitaires de faibles coûts avec des cibles très finement choisies. Une partie importante des revenus de Google provient de ce système et c’est donc bien à l’exploitation de la longue traîne dans le domaine de la publicité que la firme doit son phénoménal succès économique. De même, la société eBay qui organise la vente de millions d’objets de particulier à particulier doit aussi être vue comme une utilisatrice de la longue traîne, avec un modèle commercial sans entrepôts et sans service logistique, puisque ce sont les clients eux-mêmes qui détiennent les produits et réalisent les envois.

La longue traîne est partout et il se peut qu’elle détermine notre avenir. En effet, si la taille des catastrophes majeures suit une loi normale, alors il est vraisemblable qu’aucune ne nous détruira tous, car celles que nous avons déjà affrontées et surmontées ne sont guère moins importantes que celles qu’on peut envisager pour l’avenir (les catastrophes beaucoup plus grosses ayant une probabilité négligeable). En revanche, si la distribution des catastrophes suit une loi à longue traîne, nous pourrions être emportés par l’une d’elles : beaucoup plus importante que celles du passé, mais de probabilité non négligeable, elle se produira dans un avenir peut-être pas très lointain !

Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science n° 362 de décembre 2007.