Cryptographie, du chiffre et des lettres

Détail de la machine Enigma © B. Lord, 2008 Voici un détail de la machine Enigma utilisée par l’armée allemande pendant la seconde guerre mondiale, pour crypter ses messages. On distingue nettement les rotors qui servent à chiffrer et déchiffrer les messages secrets.

La cryptographie (« écriture secrète ») est la science des codes secrets, littéralement des codes « destinés à mettre à l’écart » ceux qui ne connaissent pas telle ou telle information. On se sert tous les jours de la cryptographie : carte bancaire, chaînes de télévision à péage, déclaration de revenus sur Internet, signature électronique, etc. La sécurité peut être en effet considérée comme la distribution de la confiance. La cryptographie permet aux gens de s’assurer que cette confiance ne sera pas compromise lors des communications.

L’histoire des codes secrets a été souvent façonnée par les militaires et les diplomates, depuis Jules César jusqu’au Téléphone rouge qui reliait le Kremlin et la Maison Blanche, en passant par le cassage (avec l’aide des Polonais) des codes de la machine Enigma de la marine allemande par les plus brillants mathématiciens britanniques, dont Alan Turing. Ce cassage, de l’aveu du Premier ministre de l’époque Winston Churchill, a accéléré l’issue de la guerre de plusieurs mois, épargnant la vie de milliers de personnes.

C’est en retraçant les grandes étapes de cette histoire des codes secrets qu’on peut comprendre l’évolution de cette science, et mettre en lumière le formidable bond en avant qu’elle a fait au XX^e siècle grâce aux mathématiciens et aux informaticiens.

Où l’on commence par marcher en rond pour réfléchir au problème

Pour tout ce qui suit, on considère que les lettres sont équivalentes à leur position dans l’alphabet : chaque lettre est donc un nombre (A vaut 1, B vaut 2, Z vaut 26, etc.). On note avec le signe % et on appelle modulo l’opération qui donne le reste de la division euclidienne entre deux nombres, soit C = A % B veut dire que A = k × B + C, avec k un nombre entier quelconque. On peut voir le modulo comme une opération qui sert à « tourner en rond » en comptant : (k × 26 + 1) % 26 = 1 .

En effet, si je suis sur un cercle divisé en 26 cases (1 secteur angulaire par lettre de l’alphabet), et qu’Alice me dit d’avancer d’un certain nombre de cases, alors Ève, qui m’observerait positionné sur ma case d’arrivée, ne pourrait pas savoir de quelle case je suis parti sans savoir le nombre secret de cases qu’Alice m’a communiqué.

Ce nombre secret de cases s’appelle « la clef ». Une lettre du message crypté (ou chiffré) correspond à ma position d’arrivée sur une certaine case du cercle. Une lettre du message non chiffré, ou « en clair », est la case du cercle dont je suis parti (que seule Alice peut calculer). Ève est appelée « le pirate », ou « l’adversaire », qu’Alice et moi avons en commun : c’est n’importe qui ne partageant pas notre secret.

Par exemple : si je suis sur la case du F (la case numéro 6), et qu’Alice me dit d’avancer de 244 cases, je vais donc me placer sur la case numéro (244 + 6) % 26 = 16 (celle de P). Dans mon message crypté, je vais écrire un P à Alice, à la place du F de mon message en clair. Et comme Alice et moi n’avons aucune raison particulière d’avoir choisi 244 plutôt que 189 543, Ève est bien embêtée.

Où Jules César montre que, face aux ignorants, assez peu de jugeote suffit

C’est du moins ce que croyait Jules César, qui était un peu prétentieux, comme le sont parfois les gens dans sa situation. Pour envoyer ses messages secrets à ses soldats sur le champ de bataille, il choisissait la même clef secrète pour toutes les lettres. Sur l’alphabet circulaire de 26 cases, il fallait toujours avancer de 3 cases. César ne trompant guère que les analphabètes et les esprits médiocres, sa technique a malgré tout été utilisée pendant des siècles. Il a pourtant commis deux erreurs : croire que les gens ne verraient jamais aucun motif particulier se répéter dans les messages chiffrés et croire qu’il pouvait se permettre de choisir son initiale, le C (3), comme secret qui cèlerait à tout jamais l’accès à la pensée secrète de César. Ce secret volé a dû apparaître aux premiers casseurs du Chiffre de César comme le signe intangible qu’ils avaient réussi.

C’est dire l’importance extrême de la « qualité de fabrication » du pseudo-hasard que l’on produit en machine. Il faut que notre secret ne dépende pas de nous : le nom de votre chat ou votre date d’anniversaire sont de mauvais choix pour constituer un bon secret. Un embrouillamini inextricable de lettres minuscules, majuscules, de nombres et de signes de ponctuation fait au contraire un excellent mot de passe.

Le problème mathématique du Chiffre de César vient du fait que toutes les lettres vont subir le même décalage par 3 sur le cercle alphabétique. Chaque lettre ne pouvant se transformer qu’en une seule autre lettre, ce code secret est appelé mono-alphabétique. Par exemple, tous les E vont devenir des H une fois chiffrés. Or, on peut se dire que le E est une lettre qui revient très souvent en latin, et qu’il y a donc de fortes chances pour que la lettre qui revient le plus souvent dans le message chiffré soit un E en clair. On peut ainsi retrouver les correspondances lettres cryptée/en clair avec leurs fréquences d’apparition respectives. Il se produit « une fuite d’information » (notion que l’Américain Claude Elwood Shannon a formalisée le premier en 1948). Il y a un trou dans l’algorithme qui laisse fuiter la clef secrète. On détecte un trou de sécurité en essayant de repérer des motifs, souvent subtils, qui se répètent. Si on est un pirate, on va tenter par contre de s’y engouffrer et de voler le secret.

Où l’on vénère Vigenère le visionnaire

Au XVI^e siècle, le diplomate Blaise de Vigenère a joué les plombiers sur l’algorithme du Chiffre de César. Son algorithme continue pourtant de fuir : il n’a fait que rajouter une rustine, mais une rustine de génie. Vigenère s’est avisé que le problème de l’algorithme de César venait du fait qu’il ne changeait jamais sa clef secrète, parce que le décalage sur le cercle était toujours le même. Alors il s’est dit qu’il fallait aussi « faire tourner la clef », mais sur son cercle à elle : Vigenère choisit un mot (pouvant être inventé) de plusieurs lettres comme clef secrète (César n’utilisait une clef que de longueur 1 lettre, et toujours égale à la lettre C : 3). Ainsi, la clef secrète pour une lettre en clair change à chaque fois, et périodiquement. Une fois qu’on a utilisé la dernière lettre de la clef secrète, on revient à la première pour chiffrer la prochaine lettre en clair, et ainsi de suite. Comme chaque lettre en clair peut potentiellement devenir plusieurs lettres différentes une fois chiffrée, on parle de « code poly-alphabétique ».

Ici, le problème est qu’il y a un motif qui se répète encore dans le message chiffré, parce que chaque lettre de la clef secrète revient périodiquement. Les répétitions dans le message chiffré apparaissent quand il est en phase avec la clef : quand une même suite de lettres du message en clair est chiffrée plusieurs fois avec la même suite de lettres de la clef secrète. En estimant la longueur des suites de lettres qui se répètent une fois chiffrées, on obtient la longueur de la clef. Le même décalage pour chiffrer revenant périodiquement, on peut se dire que le Chiffre de Vigenère n’est finalement qu’un Chiffre de César qui utiliserait périodiquement la même clef. On doit donc simplement pratiquer autant de cassages élémentaires du Chiffre de César qu’il y a de lettres dans la clef secrète. Indépendamment, le mathématicien britannique Charles Babbage eut cette idée en 1854, qu’il ne divulgua pas, jusqu’à ce que Friedrich Kasiski la retrouve par lui-même et la publie en 1863.

Plus généralement, le trou du Chiffre de Vigenère peut se boucher de deux manières :
– soit en utilisant une clef secrète de la même longueur que le texte à chiffrer ;
– soit en « pré-brouillant » les lettres qui restent à crypter à l’aide de lettres déjà cryptées. La première solution est appelée « Chiffre de Vernam » (1917). Mais il est très compliqué de gérer de longues clefs secrètes, aussi ce code secret a-t-il surtout servi pour le Téléphone rouge. Par contre, c’est le seul dont on peut prouver qu’il est étanche : il ne laisse pas fuiter une seule goutte de la clef.

La seconde piste fait l’objet de toute l’attention des chercheurs et le nouveau standard mondial depuis 2001, l’AES (inventé par les Belges Joan Daemen et Vincent Rijmen), fait encore partie de cette famille de solutions. La taille des clefs utilisées de nos jours dans l’AES est de 256 bits (les lettres de l’ordinateur valant 0 ou 1). C’est de plus un algorithme qualifié de très sûr car on ne connaît pas d’attaques performantes pour le neutraliser. Le précédent standard, le DES, mettrait aujourd’hui une petite semaine à être cassé avec des moyens de calcul informatiques raisonnables : il devenait poreux car sa clef n’était longue que de 56 bits.

Où il semblerait bien que l’on ait encore un énorme problème à résoudre

Mais il reste encore un problème, et de taille : comment Alice et moi ferons-nous pour nous communiquer notre clef secrète sans qu’Ève puisse s’en emparer ? Tous les algorithmes précédents sont qualifiés de symétriques : il faut que la clef secrète soit la même au cryptage et au décryptage. Les Américains Diffie et Hellman ont inventé la cryptographie asymétrique en 1976, mais c’est un an plus tard qu’a été inventé l’algorithme asymétrique le plus utilisé, le RSA (pour Ron Rivest, Adi Shamir et Len Adleman) : la clef n’a pas besoin d’être la même pour chiffrer que pour déchiffrer. Chacun a donc deux clefs : l’une, publique, que nous pouvons donner à tout le monde pour qu’on puisse nous écrire des messages cryptés, et l’autre, privée, que nous devons conserver précieusement et qui nous servira pour déchiffrer les messages qu’on nous envoie. Comme je suis le seul à pouvoir déchiffrer les messages qu’on m’envoie, Ève est prise au piège. C’est tout le mérite de la cryptographie à clef asymétrique que d’avoir permis une transmission sûre du secret.

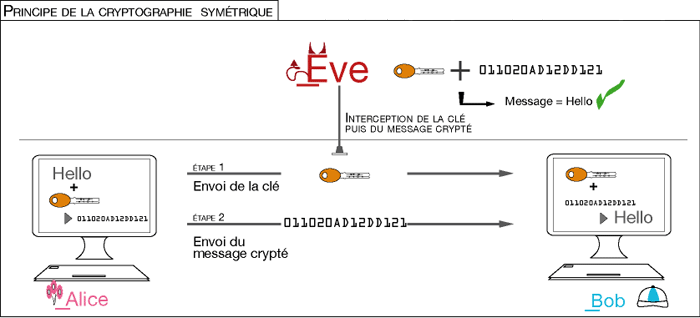
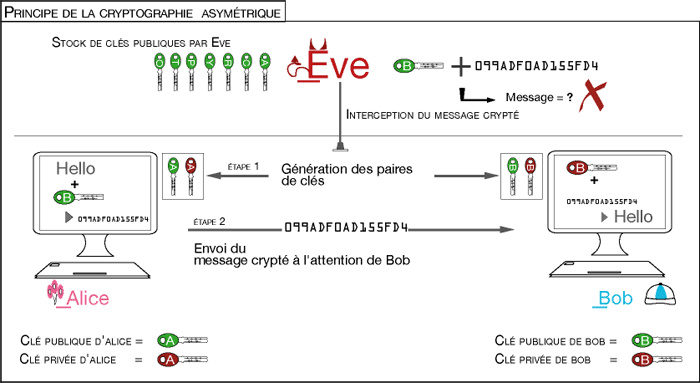
Exemples de schémas à clef symétrique ou clef asymétrique.
Images : Vivian Fayard
Dans les schémas symétriques, on peut voler la clef secrète. Dans les schémas à clef asymétrique, on ne pourra que se procurer les clefs publiques, et voler un message chiffré dont la signification restera incompréhensible puisqu’on n’aura pas eu accès à la clef privée du destinataire (clef rouge de Bob).

Mais le problème des algorithmes à clefs asymétriques est qu’ils sont vraiment très lents : ils nécessitent beaucoup de calculs. Alors, on ne les utilise que pour chiffrer un message en clair qui n’est lui-même qu’une clef secrète pour un autre algorithme, à clef symétrique cette fois. On utilise donc une combinaison d’algorithmes, par exemple RSA-AES. Pour déchiffrer, on récupère d’abord la clef pour l’algorithme symétrique à l’aide de notre clef privée, puis seulement ensuite on peut déchiffrer le message. On parle alors de cryptographie hybride. Elle est utilisée aujourd’hui pour toutes les applications nécessitant un haut degré de confidentialité.

Où allons-nous ?

Du fait du lien mathématique particulier qui existe entre les clefs privée et publique de chacun, je peux vérifier, à l’aide de la clef publique d’Alice, que c’est bien elle qui m’a écrit. On parle alors d’authentification. Enfin, Alice peut encore signer son message. La signature permet d’établir si le message tel qu’elle voulait me l’envoyer a été altéré (ou non) pendant qu’il transitait entre elle et moi. La signature électronique a aujourd’hui la même valeur juridique que la signature manuscrite dans de nombreux pays, dont la France.

Les grandes thématiques de la recherche contemporaine en cryptographie portent sur :
– des problèmes de confidentialité : les algorithmes que nous employons sont-ils sûrs ? Sont-ils troués et laissent-ils fuiter de l’information sur la clef secrète ?
– des problèmes d’authentification : comment garantir l’identité des interlocuteurs lors de leurs échanges ?
– des problèmes d’intégrité du message : Ève n’aurait-elle pas modifié le message entre le moment où Alice me l’envoie et celui où je le reçois ?

On peut citer d’autres thématiques très actives, par exemple celle consistant à partager des secrets à plus de deux personnes (il faut un certain quorum de clefs secrètes pour pouvoir décrypter). Ou bien encore la modélisation des protocoles : comment révoquer l’ensemble de ma clef asymétrique si Ève m’a volé ma clef privée ? Comment avertir les autres qu’elle a changé mais que c’est encore bien moi qui utilise dorénavant cette nouvelle paire de clefs publique/privée ?

Enfin, il est des situations où l’on peut souhaiter tout autre chose : conserver son anonymat. Par exemple, lors de l’interconnexion des bases de données : la cryptographie fournit une bonne partie des outils qui permettraient d’interconnecter anonymement des bases de données. Le conditionnel précédent n’est, hélas !, pas dû à un quelconque obstacle technique : les gouvernements méconnaissent tellement les possibilités offertes par la cryptographie qu’ils considèrent l’anonymat comme un luxe désuet et inutile. Mais une population a aussi besoin de son anonymat, pas seulement de sa sécurité. Et la cryptographie peut le lui garantir.

Dernier point : la cryptographie ne suffit pas toujours, elle ne garantit pas l’acheminement des messages…

Cet article est paru dans la revue DocSciences n°5 Les clés de la révolution numérique, éditée par le CRDP de l’Académie de Versailles en partenariat avec l’INRIA.