L’algorithme de Pledge

« Oh, zut ! Maintenant la lumière s’est éteinte ! Comment je vais faire pour sortir ? Ce n’était peut-être pas une si bonne idée d’aller me balader tout seul dans les catacombes. Tiens, l’autre jour, j’ai lu quelque chose sur le web qui expliquait comment sortir d’un labyrinthe : ça s’appelait la recherche en profondeur. Mais on avait besoin de lumière et d’une craie pour tracer des repères. Impossible donc dans ces ténèbres. Est-ce que je vais être obligé de passer la nuit ici ? »

Que faire ? D’abord, avancer prudemment tout droit jusqu’à rencontrer un mur. Puis longer ce mur en le gardant à main gauche. Voici comment on trouve la sortie de ce labyrinthe :

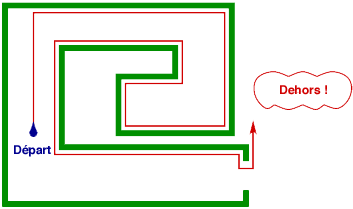
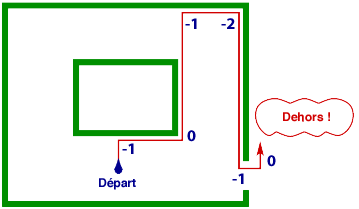
Mais… mais si on a buté sur un pilier au lieu d’un mur, on va tourner en rond pour toujours :

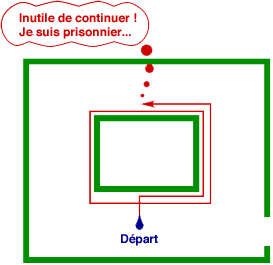
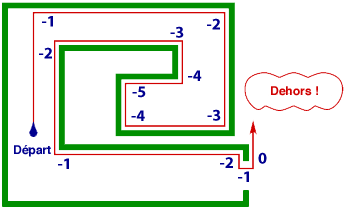
Donc ça ne va pas ! Il faut trouver un moyen de s’éloigner de ce genre de pilier. Nouvelle tentative : aller tout droit jusqu’au mur, puis le longer en suivant ses changements de direction jusqu’à ce qu’on se retrouve dans la même direction qu’au début, partir alors à nouveau tout droit. Ainsi, le pilier ne pose plus de problème :

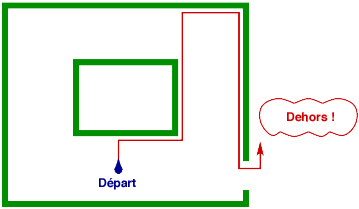
Mais là, c’est avec le premier exemple que ça ne marche plus :

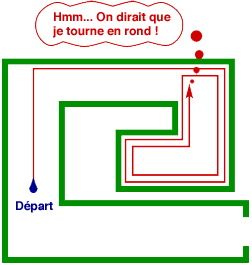
« Ca commence à être angoissant ! Quoi que je fasse, il y a toujours quelque chose qui cloche. Pourtant, il doit forcément y avoir un chemin pour sortir – puisque j’y suis entré ! »

Évidemment, il existe un chemin qui mène dehors. La question, c’est de le trouver ! Peut-on vraiment utiliser un algorithme général pour trouver l’issue de n’importe quel labyrinthe imaginable ? Et de plus, dans l’obscurité ?

Eh bien, oui, c’est possible. Mais il ne suffit pas de marcher en ligne droite. Il faut compter les changements de direction.

Supposons que, comme dans les exemples précédents, tous les angles soient droits. On n’a alors que deux possibilités, tourner à droite ou à gauche selon un angle de 90°. On compte les changements de direction en augmentant d’un point lorsque l’on tourne à gauche et en diminuant d’un point lorsque l’on tourne à droite (y compris la première fois que l’on tourne à droite quand on atteint un mur). Au début, le décompte est à zéro. Les deux instructions sont alors les suivantes :

1. Aller tout droit jusqu’au mur, passer à l’instruction 2 ;
2. Longer le mur par la droite (ou par la gauche, mais toujours dans le même sens) jusqu’à ce que le décompte des changements de direction atteigne zéro, passer à l’instruction 1 ;

Il faut répéter ces actions jusqu’à ce que l’on revienne à la lumière du jour.

Cet algorithme porte le nom de celui qui l’a découvert : un petit garçon de douze ans, qui s’appelait John Pledge.

Il ne s’applique pas seulement à ces deux exemples. Il est valable dans tous les cas ! Un raisonnement « par l’absurde » permet de le prouver. La démonstration rigoureuse en est assez complexe, elle est présentée notamment dans l’ouvrage Turtle Geometry de Harold Abelson et Andrea diSessa (en anglais). L’idée générale est que si l’on ne trouvait pas la sortie avec l’algorithme de Pledge, cela voudrait dire que l’on tournerait en rond, en suivant une boucle sans fin.

Voici pourquoi cette hypothèse n’est pas valable. Tout d’abord, notons que le chemin emprunté ne peut pas présenter de croisement. Une boucle sans croisement pourrait tourner soit dans le sens des aiguilles d’une montre, soit dans le sens inverse.

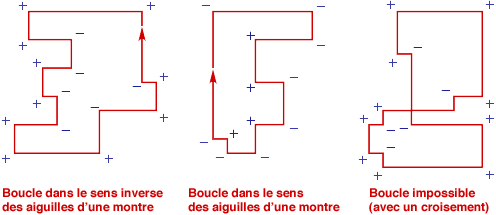
On se place dans le cas où on tourne à droite la première fois qu’on arrive à un mur. Si on effectuait une boucle sans fin dans le sens inverse des aiguilles d’une montre, il y aurait quatre changements de direction vers la gauche de plus que vers la droite. Le décompte des changements de direction pourrait donc prendre des valeurs positives. Or ceci n’est pas possible, car au moment où on rejoint un mur, le décompte passe à -1. Et dès qu’il atteint la valeur 0, on s’éloigne à nouveau du mur !

Si on pouvait suivre une boucle sans fin, celle-ci devrait donc se dérouler dans le sens des aiguilles d’une montre. Alors, à chaque nouveau passage au même sommet, le décompte diminuerait de 4, de sorte que sa valeur resterait toujours négative et ne prendrait jamais la valeur 0. On longerait donc constamment le même mur en le gardant à main gauche, sans jamais pouvoir s’en écarter. Cela signifie que dans ce cas, on aurait buté sur un mur d’enceinte sans aucune ouverture. Il n’y aurait aucun moyen de sortir, ni d’ailleurs d’entrer dans le labyrinthe !

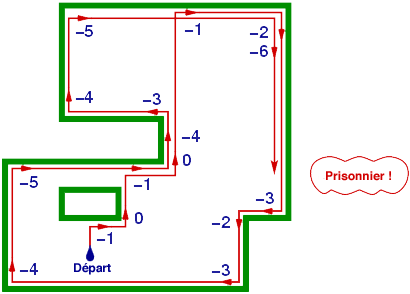
Par conséquent, s’il existe un chemin pour sortir, l’algorithme de Pledge le trouve !

Le film suivant montre comment un robot miniature de type Khepera II utilise l’algorithme de Pledge pour trouver la sortie d’un labyrinthe.

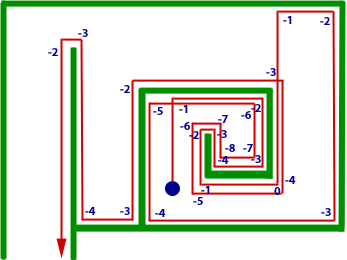Visionner la vidéo – Durée : 4 min 23 s.	Schéma du chemin suivi par le robot.

Nous vous proposons une animation en HTML5/JS pour observer la façon dont l’algorithme de Pledge permet de sortir d’un labyrinthe. Au lieu de compter les changements de direction, les angles sont additionnés en leur attribuant un signe positif ou négatif selon que l’on tourne à gauche ou à droite. Vous pouvez vérifier que les stratégies de suivi de mur ou de maintien de la direction échouent dans certaines circonstances. Vous pouvez aussi dessiner votre propre labyrinthe pour y tester les algorithmes.

Cette animation a été réalisée par Ouest INSA, sur la base de l’applet Java initialement associée à l’article, qui reste accessible ci-dessous.

Une première version de ce document est parue en allemand dans la série Algorithmus der Woche publiée à l’occasion de l’Année de l’informatique (Informatikjahr) 2006.