
Des mathématiciens à la rescousse des lagunes méditerranéennes
Les lagunes sont des systèmes complexes et essentiels qu’il convient de comprendre afin d’aider à les préserver. Des équipes internationales et multidisciplinaires font appel aux mathématiques pour y voir plus clair dans l’avenir des lagunes du bassin méditerranéen.
Les lagunes sont des étendues d’eau peu profondes reliées à la mer par des canaux étroits souvent sujets à l’ensablement. Elles sont extrêmement nombreuses en Méditerranée où elles jouent souvent un rôle important tant pour l’écologie que pour l’économie.
Un rôle écologique
Comme les autres zones humides, les lagunes ont un rôle de tampon en protégeant la côte de l’influence de la mer, en filtrant les eaux de ruissellement et en abritant d’importantes communautés végétales (algues, roseaux) et animales (mollusques, crustacés, poissons). Ce sont des zones de nidification importantes pour les oiseaux migrateurs et à ce titre, de très nombreuses lagunes sont protégées par la convention de Ramsar.
La Convention sur les zones humides d’importance internationale, appelée Convention de Ramsar, du nom de la ville d’Irak où elle a été adoptée en 1971, est un traité intergouvernemental qui sert de cadre à l’action nationale et à la coopération internationale pour la conservation et l’utilisation rationnelle des zones humides et de leurs ressources. En avril 2013, 167 pays avaient adhéré à cette convention et une superficie de 205 369 948 hectares était protégée.
Un rôle économique
Les lagunes sont des zones de production biologique intense et font l’objet d’une importante exploitation de leurs ressources. L’étang de Thau, la plus grande lagune de France, assure ainsi la production de plus de 12 000 tonnes d’huîtres par an, et les 600 établissements conchylicoles qui y sont installés emploient environ 2 000 personnes. Au nord de la Méditerranée, les lagunes font l’objet d’études et d’une surveillance attentive. La protection de la lagune de Venise est un sujet d’importance nationale pour l’Italie et la communauté européenne qui mobilisent des ressources considérables à cette fin. Les problèmes économiques que connaissent les pays du sud du pourtour méditerranéen ne leur permettent pas d’assurer le même niveau de surveillance des habitats naturels et la gestion des lagunes y est souvent très parcellaire. Pourtant, au nord comme au sud de la Méditerranée, les lagunes font face aux mêmes types de problèmes. En France, le développement de l’agriculture irriguée dans la vallée de la Durance et les rejets d’eaux douces de la centrale électrique de St Chamas ont entraîné depuis 1966 une désalinisation importante de l’étang de Berre et une dégradation importante de la santé biologique de ce milieu. Le lac Burullus en Égypte est confronté au même type de phénomène : le rejet des eaux de drainage des surfaces irriguées du Delta du Nil dans le lac a produit un changement radical de la salinité des eaux du lac. Le pourcentage de mulets capturés, espèce marine très appréciée et donc de grande valeur économique, a ainsi décrû de 44,7 % en 1963 à 17 % en 2000 pour être remplacé par la capture du Tilapia, espèce tolérant beaucoup mieux les variations de salinité mais de moins grande valeur économique.
Le tilapia est un poisson d’eau douce ou saumâtre. Il est élevé pour la pêche et la pisciculture et c’est l’un des poissons d’élevage les plus consommés au monde. Son exploitation remonterait à l’Égypte ancienne, il y a plus de 4 000 ans et les artistes de l’Égypte antique l’ont représenté sous de nombreuses formes. Cette petite bouteille en verre en forme de Tilapia date de l’époque d’Akhenaton et fait partie de la collection du British Museum.

Ce type de problème n’est pas simplement un problème affectant les amoureux du passé et les protecteurs de la nature. On estime à plus de 28 000 en 2002 le nombre de personnes vivant directement de la pêche sur le lac Burullus. De plus, les lagunes sont très souvent situées en bordure de zones densément peuplées et le rythme rapide des changements liés à l’urbanisation croissante, au tourisme, à la pêche ou à la pisciculture, met en danger l’équilibre souvent fragile qui s’était établi au fil du temps entre les différents compartiments de ces éco-systèmes.
Les mathématiques peuvent contribuer à protéger l’équilibre des lagunes
Avant toute chose, il s’agit de comprendre le fonctionnement global d’une lagune pour identifier les paramètres importants et proposer des solutions pour une gestion durable de ces milieux. Pour ce faire, à coté des techniques classiques que sont la collecte et l’analyse des données, la simulation numérique qui est du ressort du mathématicien joue un rôle de plus en plus important.
La modélisation des lagunes
Modéliser un phénomène consiste à établir un système d’équations dont la solution décrira l’évolution des différentes variables qui définissent le phénomène. Dans le cas des lagunes, on s’intéressera à la température de l’eau, à sa salinité et à sa vitesse, ainsi qu’aux différents constituants chimiques présents dans l’eau et qui peuvent influencer la vie des communautés animales ou végétales présentes dans le milieu. Le nombre de variables à considérer est pratiquement infini. En pratique, il est limité par les ressources de calcul dont on dispose ainsi que par les données recueillies sur le milieu dont l’acquisition est lente et coûteuse.
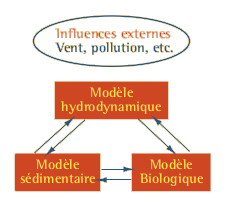
Quoi qu’il en soit, la modélisation de milieux vivants comme les lagunes est intrinsèquement un problème qui fait intervenir de nombreux phénomènes dont les échelles d’espace et de temps peuvent être très différents. De manière simplifiée, on peut considérer que la modélisation des lagunes fait intervenir au moins trois compartiments ou sous-modèles en interactions plus ou moins fortes et qui décrivent l’hydrodynamique (la manière dont les masses d’eau se déplacent), le comportement des sédiments (les matières solides en suspension ou reposant sur le fond) et la biologie du milieu. Ces trois sous-modèles sont bien évidemment soumis à des influences extérieures dont la connaissance est essentielle pour les prévisions.
Les modèles hydrodynamiques
Ces modèles sont du même type que les modèles météorologiques qui permettent de prévoir l’évolution temporelle de l’état de l’atmosphère. Ils peuvent être de complexité extrêmement variée selon que l’on considère que l’écoulement des masses d’eau est uni, bi ou tridimensionnel mais ils reposent tous sur les considérations physiques élémentaires que sont la conservation de la masse (Rien ne se perd, rien ne se crée, tout se transforme) et la seconde loi de Newton (force = masse × accélération). Le système d’équations qui en résulte ne peut être résolu de façon exacte et on est amené à discrétiser le système. De façon simplifiée, discrétiser un système consiste à découper l’espace en petits volumes élémentaires et à remplacer la connaissance des fonctions définies en chaque point de la lagune par la connaissance d’un nombre fini de variables définies dans chaque volume élémentaire.
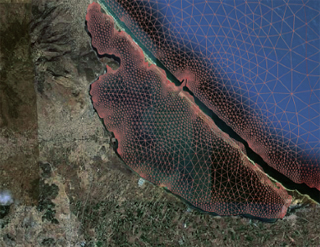
Maillage triangulaire de la lagune de Nador au Maroc. Source : travaux de Imad Elmahi, Université d’Oujda au Maroc.
Dans la figure ci-contre, on a par exemple découpé la lagune de Nador au Maroc en une succession de petits triangles. Dans chacun de ces petits triangles sont définies les valeurs de la hauteur d’eau, de la vitesse, de la température, de la salinité, etc. Ce découpage en triangles repose sur des algorithmes complexes mais aujourd’hui bien maitrisés. Il s’agit maintenant d’organiser le transfert des masses d’eau entre ces volumes pour faire évoluer le système. Cela se fait en utilisant les principes physiques précédemment évoqués (conservation de la masse, seconde loi de Newton). Les techniques mathématiques utilisées pour organiser ces transferts appartiennent à différentes familles de méthodes (dans le jargon des mathématiciens, on parle de méthodes de différences finies, de volumes finis ou encore d’éléments finis) et la recherche mathématique pour identifier de « bonnes » méthodes est un domaine très actif. Les résultats de ces calculs permettent d’obtenir à chaque instant des cartes de hauteur d’eau, de champ de vitesse, ou encore de salinité et de température.
La modélisation des sédiments

Image satellite du Lac de Tunis. Source : thèse de Paolo Cinat, Université de Pise, Italie, 2012.
Contrairement à l’océan profond ou les mouvements des sédiments n’ont que peu d’importance pour le comportement global du système, la connaissance de l’évolution du fond est fondamentale pour les régions côtières et les lagunes en particulier. En effet, l’un des plus grand dangers auxquels sont confrontés les lagunes est l’ensablement des canaux qui relient la lagune à la mer. Cet ensablement, s’il survient, signe bien souvent la mort de la lagune. En effet, les hautes températures et les forts vents qui soufflent en Méditerranée entraînent une évaporation intense, et si ces pertes ne sont pas compensées par un apport marin, la lagune se transforme très vite en une étendue d’eau saumâtre, puis en un dépôt de sel.
L’apport de la modélisation mathématique peut s’avérer ici fondamental. En effet, de nouveaux aménagements portuaires ou touristiques peuvent modifier profondément les équilibres anciens et conduire à des changements radicaux dans le transport des sédiments. Il existe un grand nombre de modèles physiques permettant de calculer les transports de sédiments mais une modélisation basée sur les principes premiers de la physique est dans la plupart des cas impossible. La compréhension des écoulements complexes contenant les deux phases solide et liquide est en effet encore largement un problème ouvert et, dans la pratique, les ingénieurs utilisent des modèles empiriques basés sur des expériences de laboratoire ou des mesures expérimentales in situ.
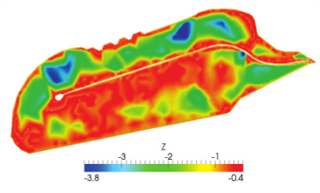
Bathymétrie du Lac Nord de Tunis.
C’est un modèle de ce type qui a été utilisé dans l’exemple de la figure ci-contre qui représente la bathymétrie du lac Nord de la ville de Tunis (image satellite ci-dessus). Ce lac peu profond est situé au sein d’une zone très urbanisée et a fait l’objet depuis les années 80 de grands projets d’aménagement urbain.
Sur le zoom de la figure ci-dessous, qui se concentre sur l’embouchure du canal de Kherredine qui relie le lac Nord de Tunis à la Méditerranée, on constate nettement que le transport de sédiment dû aux mouvement des eaux conduit à des variations importantes de la profondeur, de l’ordre de 30 cm dans les zones rouges de la figure après les quelques jours représentés dans cette simulation.
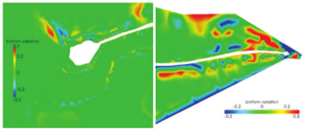
Zoom sur le canal d’entrée de la mer du Lac Nord de Tunis.
Ce phénomène, si on le laissait se poursuivre, conduirait à une fermeture de la lagune et tout au moins à un ralentissement des échanges avec la mer impliquant des changements importants dans la qualité des eaux de la lagune. Il est alors nécessaire de procéder à un dragage périodique de cette zone pour éviter la fermeture de l’accès à la mer.
Les modèles biologiques
Les lagunes sont des milieux vivants extrêmement productifs et qui abritent un grand nombre de communautés végétales et animales en interactions. Cette productivité biologique intense des milieux lagunaires a été de tout temps exploitée pour de multiples usages : récolte des roseaux, des coquillages, pêche, pisciculture, chasse et exploitation de l’avifaune. Au fil du temps, un équilibre a pu s’établir entre les diverses composantes des éco-systèmes vivants de la lagune. Cet équilibre est cependant très fragile et est à la merci de modifications minimes. Les pratiques modernes de l’agriculture intensive et l’utilisation de fertilisants chimiques, l’urbanisation des bassins versants des lagunes, le tourisme, les rejets urbains ou industriels sont des facteurs de perturbations de ces équilibres qui peuvent avoir des conséquences considérables. Comment vont réagir les éco-systèmes lagunaires à ces modifications ? Ici encore, les mathématiques peuvent être d’une aide précieuse en élaborant des modèles qui vont décrire les interactions entre les différents constituants de communautés vivantes de la lagune. Ces modèles permettent alors de comprendre les réactions des communautés végétales et animales. Ils peuvent être extrêmement complexes suivant le nombre d’espèces envisagées et le degré de détail dans la description des interactions entre espèces que l’on va considérer. Un prototype simple de ces modèles est le modèle NPZ utilisé depuis les années 1970 en océanographie biologique.
Ce système décrit l’évolution de trois composantes : la nourriture, notée \(N\), le phytoplancton, noté \(P\) et le zooplancton, noté \(Z\). Comme avec le modèle prédateur-proie de Lotka-Volterra, on décrit les taux de variation de \(N\), \(P\) et \(Z\) en fonction du temps, ce qui nous donne un système d’équations différentielles dont on peut ensuite obtenir les solutions par simulation numérique. La figure suivante résume les interactions dans le modèle.
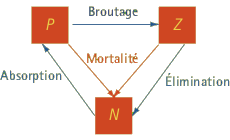
Schéma de la chaîne alimentaire dans le modèle \(NPZ\).
Ce schéma nous dit que la population de phytoplancton, \(P\), a besoin de la nourriture, \(N\) pour croître. La mortalité la fait décroître, ainsi que le broutage par le zooplancton.
On écrit ceci : \[\frac{\mathrm{d}P}{\mathrm{d}t} = f(I)g(N)P – h(P)Z – i(P)P,\] où \(f\), \(g\), \(h\) et \(i\) sont des fonctions, et \(I\) est l’intensité lumineuse. Dans le membre de gauche, \(\dfrac{\mathrm{d}P}{\mathrm{d}t}\) est le taux de variation de la population de phytoplancton par rapport au temps. Le premier terme du membre de droite décrit la contribution venant de l’absorption de la nourriture selon la quantité de lumière. Le second terme décrit la perte liée au broutage du zooplancton, et le troisième la perte liée à la mortalité. On a trois termes correspondant aux trois flèches arrivant et partant de \(P\).
Voici maintenant l’équation représentant le taux de variation de \(Z\) : \[\frac{\mathrm{d}Z}{\mathrm{d}t} = ch(P)Z – j(Z)Z,\] où \(j\) est une fonction et \(c\) est une constante. Dans le membre de droite on n’a que deux termes car on a regroupé dans la fonction \(j\) les effets de l’élimination et de la mortalité qui produisent tous deux de la matière organique. La constante \(c\) représente l’assimilation du phytoplancton par le zooplancton.
Voici enfin la troisième équation pour le taux de variation de \(N\). Comme on peut s’y attendre avec la figure, le membre de droite comporte quatre termes qui sont les négatifs de ceux observés dans \(\dfrac{\mathrm{d}P}{\mathrm{d}t}\) et \(\dfrac{\mathrm{d}Z}{\mathrm{d}t}\) : \[\frac{\mathrm{d}N}{\mathrm{d}t} = -f(I)g(N)P + (1-c)h(P)Z + i(P)P + j(Z)Z.\] Ceci nous donne toute une classe de modèles selon les fonctions \(f\), \(g\), \(h\), \(i\), \(j\) et la constante \(c\) choisies. Le choix de ces fonctions et de \(c\) dépend des caractéristiques du milieu modélisé.
Ce modèle considère trois variables d’état : la quantité de nourriture évaluée comme son équivalent azote, noté par son symbole chimique N, la quantité de plancton végétal ou phytoplancton, P, et celle de zooplancton, Z. Le système NPZ peut être considéré comme un modèle simple de la chaine alimentaire dans les lagunes et plus généralement dans les océans. Toute variation importante des quantités d’état N, P et Z est un signal d’alarme indiquant que l’équilibre entre les divers compartiments de la chaine alimentaire est rompu. Une augmentation importante du phytoplancton est ainsi souvent une conséquence des décharges incontrôlées de fertilisants issus de l’agriculture industrielle pouvant se traduire par une réduction sévère voire une disparition de certaines espèces animales vivant dans les lagunes. Ces trois variables évoluent suivant les données extérieures (température, ensoleillement,…) et des règles similaires aux équations proies-prédateurs bien connues en écologie mathématique. Bien entendu, en pratique ces modèles peuvent, suivant les milieux et les intérêts de leur concepteurs, considérer diverses sources de nourritures, par exemple azote et phosphore ou faire la différence entre diverses sources d’azote, celle d’origine naturelle ou l’azote provenant de l’agriculture irriguée ou des piscicultures.
On peut aussi distinguer entre diverses espèces animales et végétales, par exemple introduire diverses classes de phytoplancton, ou encore introduire d’autres maillons de la chaîne alimentaire par exemple, les espèces de poisson se nourrissant de zooplancton. En la matière, la difficulté consiste non pas à trouver le modèle le plus complet mais bien plutôt à construire le modèle le plus simple possible qui rende compte de façon satisfaisante des observations disponibles et qui permette des prévisions ou des explications utiles. Ces modèles biologiques doivent, bien entendu, être couplés aux modèles hydrodynamiques et de transport de sédiments décrits précédemment. La productivité biologique est en effet extrêmement sensible aux paramètres de température et de salinité que les modèles hydrodynamiques permettent de calculer mais aussi à la pénétration de la lumière dans la colonne d’eau qui est largement dépendante de la charge sédimentaire présente dans cette colonne d’eau, et ici encore, les modélisations hydrodynamiques, sédimentaires et biologiques doivent progresser de façon couplée.
Conclusion
À l’issue de ce tour d’horizon de la modélisation des lagunes, nous aimerions conclure que les mathématiques permettent une protection efficace de ces milieux. Ce serait trop optimiste. Les mathématiques et la simulation numérique permettent actuellement d’avoir une compréhension raisonnable du fonctionnement des milieux lagunaires, le pouvoir de prédiction des modèles est réel et peut être utilisé. Cependant tout cela n’est rien sans une volonté politique d’aller vers une gestion raisonnée et durable de ces milieux. Cela impose souvent un changement de mentalité et une conscience plus claire de la nécessité du respect des grands équilibres naturels. Que les mathématiques puissent aider à cette prise de conscience est une question qui dépasse le cadre de cet article.
Les travaux d’Imad Elmahi, professeur à l’Université d’Oujda au Maroc sur la modélisation de la lagune de Nador et la thèse de Paolo Cinat soutenue à l’Université de Pise, Italie ont été réalisés dans le cadre du projet Euroméditerranée 3+3 MedLagoon soutenu par Inria, l’université de Pise en Italie, le Centre National de la Recherche Scientifique et Technique (CNRST) du Maroc et le Ministère de l’Enseignement Supérieur et de la Recherche de Tunisie.
Une première version de ce document est parue dans la revue Accromath réalisée par l’Institut des sciences mathématiques et le Centre de recherches mathématiques du Québec, Volume 8.2, été-automne 2013.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Hervé Guillard