Modèles globaux ou régionaux : comment zoomer le climat ?

Le réchauffement climatique dans les régions

Le cinquième rapport d’évaluation du GIEC prévoit une augmentation de la température moyenne de la Terre comprise entre environ 1,0°C (scénario optimiste) et 4,1°C (scénario pessimiste) au cours du XXI^e siècle, s’accompagnant d’une montée du niveau des mers de 26 à 82 cm. Ce changement rapide du climat mondial s’accompagne de catastrophes naturelles (cyclones, sécheresses, inondations…) plus fréquentes  dans certaines parties du monde. Entre autres conséquences, ces événements extrêmes peuvent être la cause d’une désorganisation radicale de l’agriculture, de grands mouvements de populations abandonnant les régions frappées par les catastrophes (régions inondées et zones soumises à la désertification) pour des zones moins touchées, de problèmes de santé (désorganisation système de santé, stress…) et des tensions politiques exacerbées. La vulnérabilité des systèmes naturels et sociaux à ces événements extrêmes et leur capacité d’adaptation varient entre régions géographiques et entre populations. Il est donc essentiel de bien comprendre comment le climat évolue à l’échelle régionale pour mieux comprendre les contraintes qui s’appliquent à ces sociétés.

De l’échelle du globe terrestre à celle des régions

Les projections climatiques qui servent de base à l’élaboration du rapport d’évaluation du GIEC reposent sur des modèles climatiques globaux. Ces modèles consistent en la représentation numérique de la planète et des interactions entre l’atmosphère, l’océan et les surfaces continentales, interactions qui gouvernent l’évolution du climat. L’espace géographique numérique est composé de cases, appelées les mailles (à la manière des pixels d’une photo). Les interactions entre mailles sont modélisées par un certain nombre d’équations mathématiques, qui traduisent la conservation de diverses quantités physiques (masse, énergie, quantité de mouvement, etc.). Plus la maille est petite, plus le modèle est précis. L’effet des phénomènes météorologiques d’échelle inférieure à la maille (qui sont flous si on zoome la photo) est pris en compte grâce à des termes qui sont ajoutés aux équations de conservation. Un modèle climatique cherche à approcher le plus possible la réalité, il essaie de représenter au mieux les forces qui induisent les mouvements atmosphériques, océaniques ou terrestres. Pour cela, le modèle part de conditions initiales connues des variables climatiques telles que le vent, la température, le rayonnement, l’humidité… et les fait évoluer en résolvant les équations mathématiques.

Le modèle climatique peut couvrir l’ensemble du globe, avec pour contrepartie d’utiliser des mailles de taille relativement grossière (supérieure à 100 km).  Dans ce cas, il s’agit d’un modèle de climat global. La résolution (la taille du pixel) de ce type de modèle induit une représentation trop grossière du relief, des côtes mais aussi de l’occupation des sols. Ceci limite les études des événements extrêmes, les études d’impact et de stratégies d’adaptation associées aux changements climatiques. Or produire de l’information à l’échelle régionale est indispensable car l’adaptation aux changements repose en grande partie sur les initiatives locales. Cette démarche nécessite des résolutions beaucoup plus fines, autour de 10 km, pour pouvoir bien décrire le relief, le trait de côte qui sépare la mer du continent, l’occupation des sols dont les zones urbaines. Dans ce cas, il est judicieux d’utiliser un modèle climatique couvrant  uniquement une région, avec comme avantage d’utiliser une maille de taille fine (inférieure à 20 km). Dans ce cas, il s’agit d’un modèle de climat régional.

Lorsqu’un climat régional est utilisé pour raffiner spatialement les simulations issues d’un modèle de climat global, on parle alors de désagrégation dynamique. Il s’agit en quelque sorte d’un « zoom » sur une région particulière. C’est ce que représente schématiquement la figure 1. Elle illustre le guidage par le modèle climatique global (à droite) du modèle climatique régional (à gauche).  Le modèle climatique global fournit l’évolution de l’état de l’atmosphère à grande échelle (vent, température, pression, humidité), ce qui signifie que les fluctuations de fines échelles (inférieures à 100 km) sont absentes, un peu comme si on limitait le nombre de pixels sur une photo : l’atmosphère est décrite de façon peu détaillée. Le modèle climatique régional utilise cette information pour simuler les phénomènes de petite échelle correspondant à cet état de l’atmosphère, tels que les précipitations, les orages, les vents de montagne…

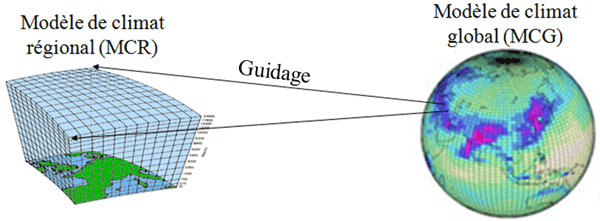
Figure 1. Guidage du modèle climatique régional par le modèle climatique global : le modèle climatique global fournit l’évolution de l’état de l’atmosphère à grande échelle que le modèle climatique régional utilise pour simuler les phénomènes de petite échelle (tels que les orages…).

Le guidage consiste à contraindre le modèle climatique régional à ne pas s’écarter de la trajectoire imposée par le modèle climatique global. Cette trajectoire est en pratique l’évolution de l’état atmosphérique de grande échelle. Ce guidage se traduit mathématiquement par l’ajout un terme dit « de relaxation » dans les équations d’évolution du vent, de la température, de l’humidité… C’est un terme non physique qui nécessite l’ajustement ad-hoc d’un coefficient de guidage (inverse à un temps de guidage). Si ce coefficient de guidage est fort, alors le modèle climatique régional est tellement contraint par le modèle climatique global qu’il ne pourra pas simuler de phénomènes de petite échelle. Si au contraire, le coefficient de guidage est très faible, alors le modèle climatique régional va « faire ce qu’il veut » indépendamment de l’évolution de l’état atmosphérique de grande échelle imposé par le modèle climatique global. Le modèle climatique régional va alors produire des phénomènes de petite échelle mais qui n’auront rien à voir avec l’état atmosphérique de grande échelle. Cet effet est illustré sur la figure 2, qui montre la corrélation entre les précipitations simulées par un modèle climatique régional non guidé et les mesures de ces précipitations aux États-Unis d’Amérique sur une année. Si les précipitations sont parfaitement simulées le coefficient de corrélation vaut 1 (rouge foncé), si les précipitations n’ont rien à voir avec celles observées le coefficient vaut 0 (bleu foncé). La résolution horizontale du modèle climatique régional (la taille du pixel) est dans l’exemple égale à 36 km. On constate qu’hormis près des reliefs de l’ouest américain, le coefficient de corrélation est très faible (<0.3) ce qui veut dire que du fait de l’absence de guidage, le modèle climatique régional désobéit au modèle climatique global et ne produit pas de précipitations en lien avec l’évolution de l’état atmosphérique de grande échelle.

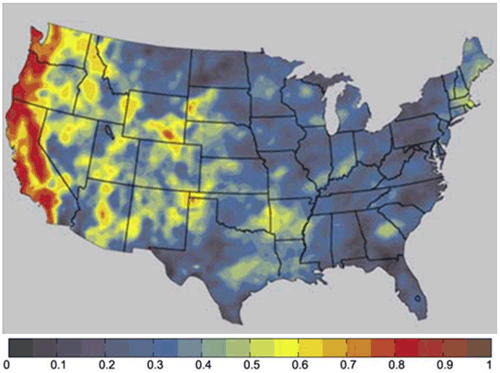
Figure 2. Coefficient de corrélation entre les précipitations simulées par un modèle climatique régional non guidé et les mesures de ces précipitations aux États-Unis d’Amérique sur une année.
Source: Lo et al. (2008).

Optimisation du zoom

Dès lors, la question cruciale porte sur l’ajustement du coefficient de guidage permettant au modèle climatique régional de ne pas trop s’écarter de l’état atmosphérique de grande échelle fourni par le modèle climatique global sans pour autant inhiber la simulation des phénomènes de petite échelle (figure 3).

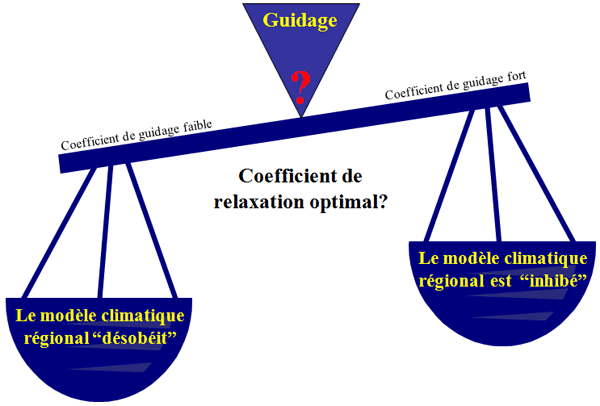
Figure 3. Schéma illustrant la problématique du guidage d’un modèle climatique régional par un modèle climatique global. Existe-t-il un compromis permettant au modèle climatique régional de ne pas trop s’écarter de l’état atmosphérique de grande échelle fourni par le modèle climatique global sans pour autant inhiber la simulation des phénomènes de petite échelle ?

Une autre question fondamentale porte sur le choix des variables de guidage. Est-il nécessaire de relaxer l’ensemble des équations et des variables climatiques (vent, température, humidité, etc.) ou bien existe-t-il un sous-ensemble de variables clés à guider ?

Les travaux ont été conduits avec un modèle outrageusement simplifié (Salameh et al., 2010), puis avec un modèle semblable aux premiers modèles de prévision du temps utilisés dans les années 50 (Omrani et al., 2012), enfin avec un modèle climatique régional de recherche (Omrani et al., 2013; 2015). Les résultats ont permis d’une part de montrer l’existence d’un coefficient de guidage optimal permettant d’assurer le meilleur compromis entre la trajectoire imposée et la nécessité de produire des phénomènes de petite échelle. Ces études ont également servi à déterminer la valeur de ce coefficient de guidage, qui peut varier entre les modèles mais qui néanmoins est inversement proportionnel à un temps de guidage de quelques heures. Elles ont enfin montré comment choisir les variables clés de l’état atmosphérique de grande échelle qu’il est nécessaire de guider. Ainsi le vent et la température sont des variables essentielles à guider car elles permettent de façon indirecte de connaitre la  pression et donc d’avoir une représentation juste de l’état de l’atmosphère. Guider l’humidité s’est avéré avoir des effets positifs sur certaines variables simulées par le modèle climatique régional, comme la précipitation, mais des effets majoritairement négatifs sur d’autres variables telles que le vent et la température. Pour illustrer l’importance du guidage, la figure 4 est similaire à la figure 2 précédente mais les précipitations ont cette fois été simulées avec un modèle climatique régional guidé avec un coefficient de guidage correspondant à un temps de guidage d’une heure. Cette fois le coefficient de corrélation est pratiquement partout supérieur à 0,6 ce qui traduit une amélioration très significative de la simulation des précipitations et de leur variabilité temporelle.

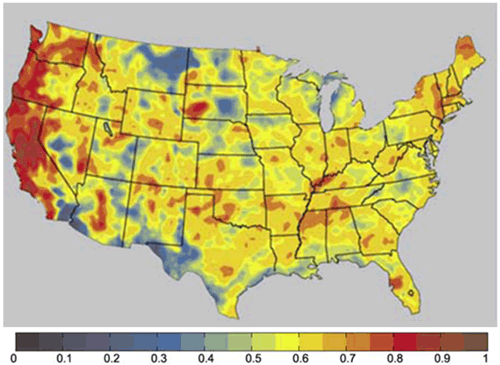
Figure 4. Coefficient de corrélation entre les précipitations simulées par un modèle climatique régional guidé et les mesures de ces précipitations aux États-Unis d’Amérique sur une année.
Source : Lo et al. (2008).

Le développement de méthodologies performantes pour élaborer des projections climatiques à une résolution spatiale très fine (inférieure à 10 km) constitue un domaine de recherche à part entière au cœur duquel on trouve les sciences mathématiques et numériques. Qu’il s’agisse de désagrégation dynamique ou de désagrégation basée sur des approches statistiques ou mixtes, ou bien encore de stratégies de gestion des risques climatiques (précipitations intenses et crues, sécheresses, canicules) ou de transition énergétique (ressources énergétiques éoliennes, solaire, hydraulique, marines, etc.), les enjeux sont essentiels pour produire des informations climatiques de qualité permettant d’élaborer et mettre en œuvre des plans d’action d’adaptation au changement climatique dans les territoires.