Un éclairage mathématique sur la dynamique des lasers
Une première version de ce document est parue dans la revue Accromath réalisée par l’Institut des sciences mathématiques et le Centre de recherches mathématiques du Québec, Volume 10.1, Hiver-printemps 2015. Nous la republions ici à l’occasion de l’année internationale de la lumière année internationale de la lumière et des techniques utilisant la lumière.
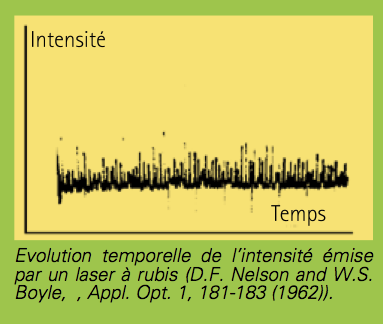
Beaucoup de chercheurs qui étudient des lasers ont été confrontés à l’apparition de fluctuations rapides d’intensité dans le faisceau de sortie du laser. Ce type de comportement était déjà évident lors des toutes premières recherches. L’intensité de la lumière produite par le laser à rubis mettait en évidence des impulsions erratiques comme le montre la figure ci-dessous.
Un laser à rubis est un laser qui utilise un rubis synthétique comme milieu amplificateur solide. Le tout premier laser opérationnel était un laser à rubis fabriqué le 16 mai 1960 par Theodore Maiman au Hughes Research Laboratories à Malibu (Californie).
Ces impulsions étaient-elles le résultat des fluctuations de l’environnement mécanique ou thermique ou bien étaient-elles le résultat d’une propriété intrinsèque du laser ? Après de nombreuses années de recherche, nous comprenons maintenant que ces oscillations proviennent principalement de forces qui régissent l’interaction entre le rayonnement et la matière. Les lasers que nous utilisons aujourd’hui sont parfois instables et certains sont très sensibles à la moindre perturbation extérieure. Ces instabilités n’ont pas d’effet sur un lecteur de codes barres ou un lecteur de CD. Elles peuvent cependant être une nuisance pour la communication par des fibres optiques car le faisceau laser, devant parcourir des kilomètres, doit être très stable. Aujourd’hui, les ingénieurs et les physiciens savent contrôler ces instabilités et même les utiliser pour des applications.
Nous disposons également de modèles mathématiques simples qui permettent de guider nos expériences. Ceux-ci se fondent sur les équations cinétiques du laser.
Une première au cinéma

James Bond, interprété par Sean Connery, est allongé sur une table et risque l’émasculation par un rayon qui remonte depuis ses pieds jusqu’à son entrejambe.
Le film Goldfinger (1964) était le premier film à montrer un laser. Les lasers n’existaient pas en 1959 quand le livre a été écrit, pas plus que les lasers industriels de forte puissance au moment où le film a été réalisé. Dans le roman, Goldfinger utilise une scie circulaire mais les cinéastes ont décidé de la changer par un laser. Le faisceau laser lui-même était un effet d’optique ajouté en post-production. Pour les gros plans où la flamme traverse la table métallique, un technicien tient un chalumeau sous la table.
Modélisation de la dynamique
Une modélisation utilisant une loi de conservation est une modélisation où la variation d’une quantité \(X\) dans un intervalle de temps \(\Delta T\) correspond à la différence entre le gain et la perte de \(X\) pendant cet intervalle.
![]()
Pour obtenir une modélisation de la dynamique du laser utilisant une telle loi de conservation, considérons le cas où \(X = n\) est le nombre de photons du laser et posons \(N=N_2-N_1\) où \(N_1\) est le nombre d’atomes dans l’état fondamental et \(N_2\) le nombre d’atomes dans l’état excité.
Le gain de photons se fait par interaction matière-lumière et est égal à
\[GNn \Delta T\]
où \(G\) est le coefficient de gain. La perte de photons, quant à elle, est due à un ensemble de facteurs (par exemple, la dispersion) et vaut, dans notre modèle,
\[\frac {n}{T_c} \Delta T\]
où le paramètre \(T_c\) est le temps que les photons passent dans la cavité du laser.
La variation de \(n\) est alors

En divisant cette équation par \(\Delta T\) et en prenant la limite \(\Delta T \to 0\), nous obtenons l’équation différentielle pour \(n\)
\[\frac{dn}{dT} =GNn- \frac{n}{T_c}.\]
D’autre part, l’équation différentielle pour \(N\) est
\[ \frac{dN}{dT} = R_p – \frac{1}{T_1} N-GNn \]
où \(T_1\) est le temps caractéristique des atomes excités pour revenir à l’équilibre et \(R_p\) est le paramètre de pompe qui correspond à la source d’énergie extérieure.
Par des changements d’échelles des variables d’état et de temps, nous transformons ces deux équations sous leur forme sans dimension :
\[ \left \{ \begin{array}{r} \frac{dl}{dt}& = & (D-1) I \\ \frac {dD}{dt} & = & \gamma (A-D-DI) \end{array} \right . \]
où \(I = 2GT_1n\) et \(D = GTN\) sont les nouvelles variables d’état, \(t = T /T_c\) est la nouvelle variable de temps et \(A = GT_cR_pT_1\) ainsi que \(\gamma = T_c/T_1\) sont les nouveaux paramètres.
Ce sont deux équations qui décrivent l’évolution de la densité des photons dans la cavité laser (intensité I) et celle des atomes excités (D) qui produisent ces photons.
Ces équations différentielles ordinaires sont non linéaires à cause des termes DI. Deux paramètres apparaissent dans ces équations, A est directement proportionnel à \(R_p\) le paramètre de pompe et est le paramètre de contrôle. Il est, par exemple, proportionnel au courant électrique appliqué à un laser à semi-conducteur. Le laser est OFF (ON) lorsque \(A < 1 (A > 1).\) Le second paramètre \(\gamma=T_c/T_1\) est le rapport entre les deux échelles de temps. Pour la plupart des lasers utilisés aujourd’hui (CO2, état solide, ou semiconducteur), \(\gamma\) est typiquement de l’ordre de 10−3. Nous pouvons déterminer les états stationnaires.
Un état stationnaire d’un système d’équations différentielles
\[ \left \{ \begin{array}{l c r} \frac{dx}{dt} & = &f(x,y) \\ \frac {dy}{dt} & = & g(x,y) \end{array} \right . \]
est une solution où chaque composante est constante : \((x(t); y(t)) = (x_0; y_0).\) Ceci implique
\[ \left \{ \begin{array}{l c r} \frac{dx(t)}{dt} & = & \frac{dx_0}{dt}= 0 \\ \frac {dy(t)}{dt} & = & \frac{dy_0}{dt}= 0 \end{array} \right . \]
On peut donc trouver les états stationnaires par la résolution du système d’équations
\[ \left \{ \begin{array}{l c r} f(x,y)& = & 0 \\ g(x,y)& = & 0 \end{array} \right . \]
Ceux-ci vérifient les équations
\[ \left \{ \begin{array}{r c l} \frac{dl}{dt} & = &(D-1) I \\ \frac {dD}{dt}& = &\gamma (A-D-DI) \end{array} \right . \]
avec \(dI/dt=0\) et \(dD/dt=0.\) Nous avons ainsi deux équations algébriques pour I et D
\[ \left \{ \begin{array} (D-1) I = 0 \\ (A-D-DI) = 0 \end{array} \right . \]
La première équation est satisfaite si (a) \(I=0\) ou si (b) \(D=1.\) En utilisant la deuxième équation, nous trouvons l’expression de la variable manquante. Les états stationnaires sont donc :
a) \(I = 0\) et \(D = A;\)
b) \(I = A-1 \geq 0\) et \(D = 1.\)
L’inégalité dans b) est imposée pour des raisons physiques : une intensité (nombre de photons) est toujours positive.
Nous pouvons ensuite analyser la stabilité linéaire de ces états stationnaires en déterminant comment une toute petite perturbation va évoluer dans le temps. Si la perturbation évolue vers zéro, nous disons que l’état est stable.
Si au contraire, la perturbation croît dans le temps, nous parlons d’un état instable. Cette analyse se fait à partir des équations originales
\[ \left \{ \begin{array}{r c l} \frac{dl}{dt} & = &(D-1) I \\ \frac {dD}{dt}& = &\gamma (A-D-DI) \end{array} \right . \]
et les résultats sont résumés dans la figure suivante.
Calculons la stabilité linéaire de l’état stationnaire \(I = 0\) et \(D = A.\) Posons
où \(\alpha(t)\) et \(\beta (t)\) sont les petites perturbations dépendant du temps. Nous allons remplacer \(I\) par \(\tilde{I}\) et \(D\) par \(\tilde{D}\) dans les deux équations :
\[ \left \{ \begin{array}{r c l} \frac{dl}{dt} & = &(D-1) I \\ \frac {dD}{dt}& = &\gamma (A-D-DI) \end{array} \right . \]
On obtient alors :
\[ \begin{array}{r c l} \frac{d \tilde{l}(t)}{dt} & = & \frac{d \alpha (t)}{dt} \\ & = & (A+\beta(t)-1)\alpha(t), \\ \frac{d \tilde{D}(t)}{dt} & = & \frac{d \beta (t)}{dt} \\ & = & -\gamma (A \alpha (t) +\beta (t) + \alpha (t) \beta (t)). \end{array} \]
En gardant uniquement les termes linéaires (c’est-à-dire de degré 1) nous avons le système
\[ \begin{array}{r c l} \frac{d \alpha (t)}{dt} & = & (A-1) \alpha (t), \\ \frac{d \beta (t)}{dt} & = & -\gamma (A \alpha (t) +\beta (t)). \end{array} \]
L’équation pour \(\alpha(t)\) a comme solution \(\alpha (t) = \alpha_0e^{(A-1)t}\) (où \(\alpha_0 \neq 0\) est la valeur initiale en \(t = 0\) de \(\alpha(t)\) et nous voyons donc que si \(A < 1\) la perturbation décroit vers \(0\) lorsque \(t\) augmente. Par contre, si \(A > 1,\) alors la perturbation augmente avec le temps et on dit que la solution stationnaire \((0, A)\) est instable. L’équation en \(\beta\) a comme solution
\[\beta (t) = \left ( \beta_0 + \frac{\alpha_0 A \gamma}{A-1+\gamma} \right ) e^{-\gamma t} – \frac{\alpha_0 A \gamma}{A-1+\gamma} e^{(A-1)t}, \]
(où \(\beta (0) = \beta_0).\) Sa croissance/décroissance dépend aussi de la valeur de A de la même manière que \(\alpha(t).\)
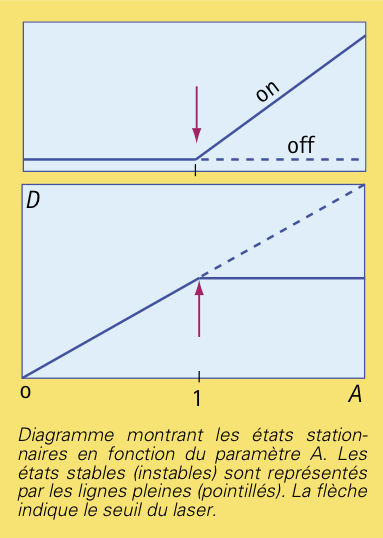
Pour les physiciens, le point A = 1 de la figure ci-dessus est appelé seuil du laser : un laser n’est actif que si le paramètre de pompe dépasse la valeur critique A = 1. Le courant électrique d’un laser à semiconducteur doit être suffisamment élevé pour que les atomes soient dans un état excité. Pour les mathématiciens, le point A = 1 est appelé point de bifurcation parce que la solution d’intensité nulle échange sa stabilité avec la solution non nulle. Le diagramme de cette figure est appelé diagramme des bifurcations. Nous apprenons de ce diagramme que l’état « ON » est toujours stable. Mais cette observation est trompeuse. La figure « Oscillations décroissantes pour I(t) » montre une simulation numérique des équations
\[ \left \{ \begin{array}{r c l} \frac{dl}{dt} & = &(D-1) I \\ \frac {dD}{dt}& = &\gamma (A-D-DI) \end{array} \right . \]
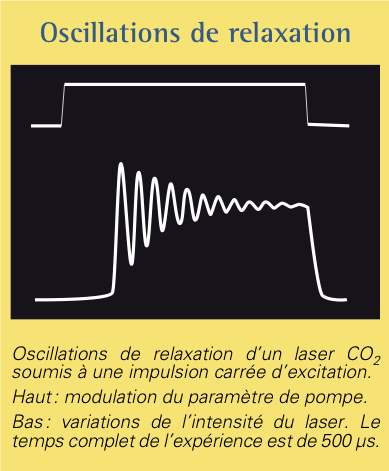
Suite à une faible perturbation de l’état stationnaire « ON », nous observons des oscillations de grande amplitude qui décroissent lentement avec le temps. La raison de ce comportement dramatique est la faible valeur de \(\gamma\) qui force nos deux variables à opérer sur deux échelles de temps distinctes. L’état stationnaire « ON » est bien stable mais une petite perturbation conduit à une évolution violente qui explique la haute sensibilité des lasers à la moindre perturbation. Ces oscillations sont appelées « oscillations de relaxation » par le physicien (voir figure ci-contre).
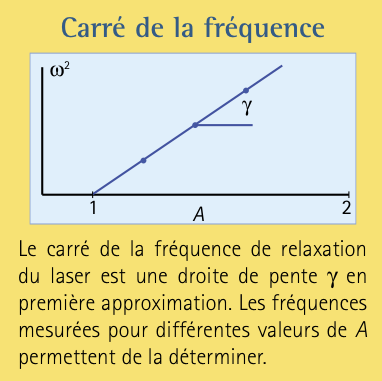
Une quantité précieuse à mesurer est la fréquence de ces oscillations parce que l’analyse de stabilité linéaire nous propose une bonne approximation donnée par \(\omega =\sqrt{\gamma (A-1)}.\)
En mesurant la fréquence pour différentes valeurs de A, nous pouvons déterminer \(\gamma\) comme la pente de la droite \(\omega^2 =\gamma (A-1)\) de la figure ci-dessous.
L’étude mathématique de la dynamique des lasers est un sujet très actif. Elle utilise et stimule des découvertes en théorie des systèmes dynamiques, entre autres pour les équations à retard. De plus, c’est un champ d’étude où les modélisateurs travaillent en proche collaboration avec les chercheurs en laboratoire, créant ainsi des interactions bénéfiques pour les deux approches scientifiques. Les multiples applications du laser dans la vie de tous les jours et dans des domaines de technologie de pointe vont continuer de générer des défis pour les chercheurs en dynamique des lasers.
- R. J. Collins, D. F. Nelson, A. L. Schawlow, W. Bond, C. G. B. Garett, et W. Kaiser, Coherence, narrowing, directionality, and relaxation oscillations in the light emission from ruby, Phys. Rev. Lett. 5, 303-305 (1960).
- D. F. Nelson et W. S. Boyle, A continuously operating ruby optical laser, Appl. Opt. 1, 181-183 (1962).
- T. Erneux et P. Glorieux, Laser Dynamics, Camb. Univ. Press, Cambridge UK (2010).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Pietro-Luciano Buono
Professeur de mathématiques à l'Institut universitaire de technologie de l'Ontario.