Planifier grâce au bavardage

Plusieurs amis se rencontrent au mois d’août dans un camping de bord de mer. À la fin du séjour, ils s’échangent leurs numéros de téléphone et promettent de s’y retrouver l’été suivant. Le printemps venu, ils essaient de se mettre d’accord sur une date de vacances commune pour l’été prochain : fin juillet ou début août ? Supposons qu’ils ne peuvent communiquer que par téléphone, ce qui n’est pas très réaliste à l’époque de Doodle, Facebook et WhatsApp, certes, mais c’est une métaphore. On peut imaginer que ce sont les assistants personnels de nos amis qui cherchent la date, et eux ne peuvent communiquer que point à point. Combien d’appels sont alors nécessaires pour que chacun connaisse les dates préférées des autres ? Cette énigme s’appelle le « gossip problem », ou le problème du bavardage.

Au-delà d’un casse-tête amusant, le problème du bavardage est important en théorie des réseaux et en bases de données réparties : par quels mécanismes peut-on s’assurer qu’une information est partagée par un ensemble de bases de données ? Récemment, notre équipe de recherche s’est intéressée au bavardage sous un autre angle. En effet, des communications de ce type interviennent dans de multiples scénarios impliquant des entités autonomes appelées agents, avec des connaissances incomplètes.

Le cas de deux amis

Prenons une version simplifiée du problème où le groupe est constitué de seulement deux amis. C’est alors très simple : un seul appel suffit pour que les dates deviennent connaissance partagée, c’est-à-dire que chacun connaisse les deux dates, la sienne et celle de son ami. Mieux, après cet unique appel les deux dates deviennent également connaissance partagée d’ordre deux : le premier ami sait que le second connaît ses dates et inversement. Mieux encore, ces dates deviennent connaissance partagée d’ordre trois : le premier sait que le second sait que le premier sait, et inversement. En généralisant, nous disons que les dates deviennent connaissance partagée d’ordre k, pour n’importe quel entier k, donc pour n’importe quel niveau d’imbrication de la modalité de connaissance.

La psychologie sociale a montré que de tels raisonnements sur les connaissances d’ordre supérieur sont fondamentaux dans l’interaction entre agents : l’absence (communément supposée chez les autistes) d’une telle théorie de l’esprit rend difficiles la communication et la compréhension mutuelle. Par exemple, après une catastrophe ou un attentat, on peut imaginer un groupe d’amis essayant de savoir si chacun va bien. Il est alors tout à fait réaliste qu’un ami ne se contente pas de savoir que tout le monde va bien : il aimerait aussi rassurer les autres et apprécierait donc qu’il y ait connaissance partagée d’ordre deux (telle que tout le monde sait que tout le monde sait que tout le monde va bien) ; voire d’ordre trois ou au-delà.

Le cas de trois amis

Si le groupe est maintenant constitué de trois amis, trois appels sont nécessaires pour arriver à la connaissance partagée d’ordre un. Par exemple, Antoine appelle Béa, puis Béa appelle Claude, et finalement Antoine appelle Claude (notons que le choix d’une personne en particulier comme initiateur de l’appel n’a aucune importance). Dans ce cas restreint, on peut facilement énumérer toutes les possibilités pour se convaincre qu’il est impossible d’arriver en moins de trois appels à une connaissance partagée d’ordre un. Notre protocole à trois appels est donc optimal. Cependant, à la fin, nous n’obtenons pas une connaissance partagée d’ordre deux : Béa ne sait pas qu’Antoine a appelé Claude, et ignore donc si Antoine connaît les dates de Claude. En effet, nous supposons que pendant un appel, les amis ne parlent que de dates, et non par exemple de l’ordre des appels qui suivront ; plus généralement, nous avons supposé que les amis ne connaissent pas le protocole. Pour obtenir une connaissance partagée d’ordre deux, un quatrième appel doit être passé entre Béa et Antoine, ou bien entre Béa et Claude. De plus, pour optimiser les échanges, les amis ne doivent pas se communiquer uniquement les dates préférées dont ils ont eu connaissance, ils doivent également se communiquer des connaissances à propos des dates. Ainsi, lors du quatrième appel, par exemple entre Béa et Antoine, il faut qu’Antoine dise à Béa que Claude connaît les dates d’Antoine ; autrement, il faudrait un cinquième appel entre Béa et Claude. En règle générale, pour obtenir la connaissance partagée d’ordre k+1, il faut que les amis se communiquent des connaissances d’ordre k.

Le cas de quatre amis

Si le cas à deux amis est direct, celui à trois un peu plus complexe, quel protocole peut-on élaborer pour quatre amis ? Une première version non optimale est de définir un protocole où tout le monde appelle tout le monde, ce qui correspond aux six appels suivants : Antoine appelle Béa, Antoine appelle Claude, Antoine appelle Diane, Béa appelle Claude, Béa appelle Diane, Claude appelle Diane.

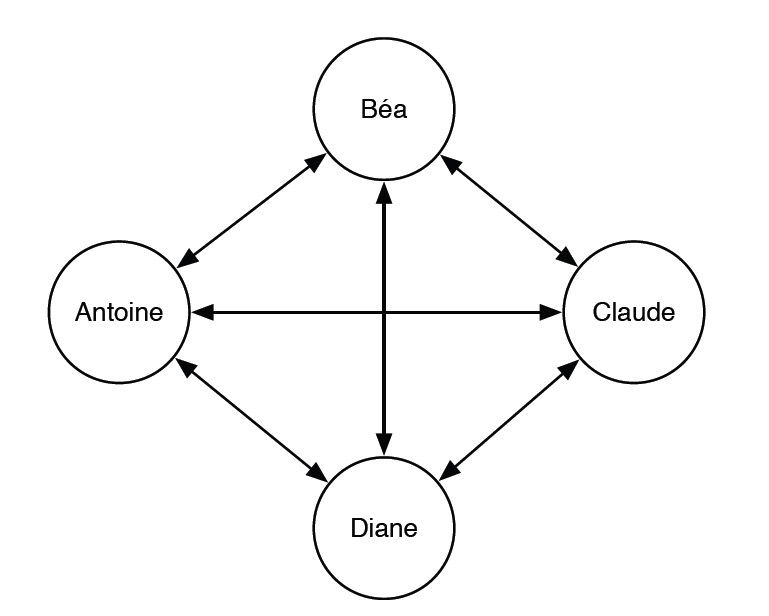
Or on peut faire bien mieux : quatre appels peuvent suffire. Dans un premier temps, Antoine et Béa s’appellent ainsi que Claude et Diane ; ensuite Antoine et Claude s’appellent ainsi que Béa et Diane. À chaque fois, ils s’échangent les informations et tout le monde a ainsi le résultat en quatre appels.

Le cas de n amis

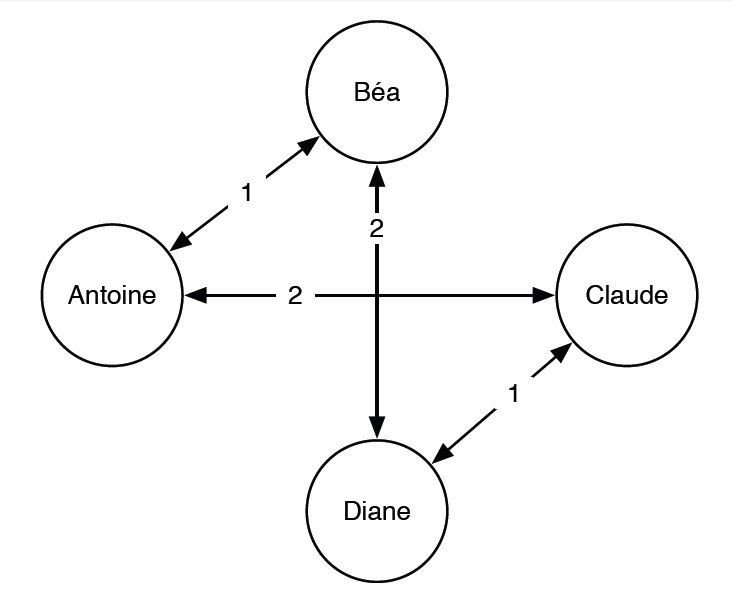
Ce protocole peut être généralisé au cas de n amis. La version non optimale nécessiterait n(n-1)/2 appels, tandis que le protocole optimal requiert seulement 2(n-2) appels. Supposons pour simplifier que n est un nombre pair : le groupe peut être séparé en deux sous-groupes de n/2 = m amis. Notons (i,j) un appel entre l’ami i et l’ami j. Le protocole est le suivant :

Dans une première étape, le premier ami de chaque sous-groupe (appelons-les ami 1 et ami (m+1)) appelle les (m-1) amis de son sous-groupe. Puis, dans une deuxième étape, l’ami 1 appelle l’ami (m+1) pendant que l’ami m appelle l’ami 2m. Au bout de la seconde étape, les amis 1, m, m+1 et 2m sont des « experts » : ils connaissent toutes les dates.

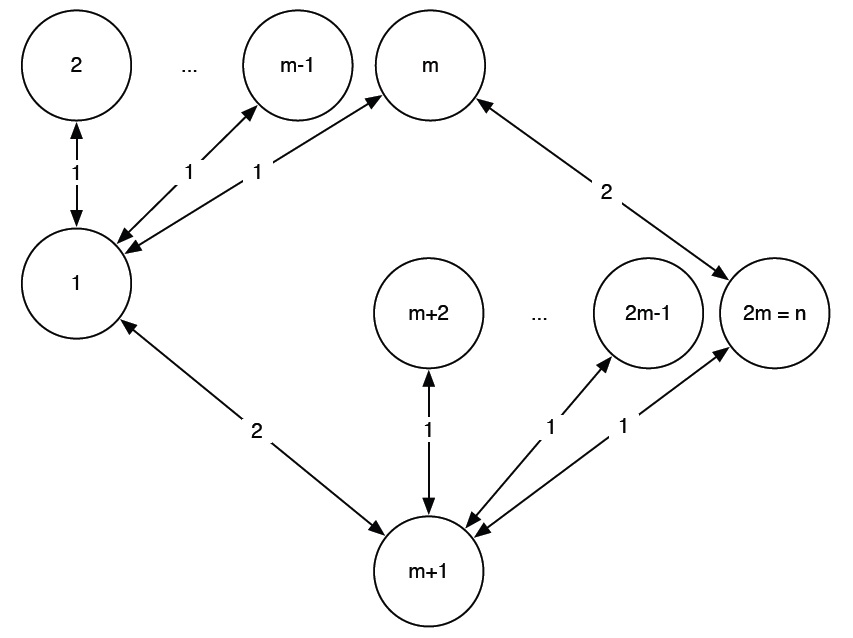
Enfin, dans une troisième et dernière étape, les experts partagent leurs connaissances avec les autres : l’ami 1 et l’ami (m+1) appellent les (m-2) amis de leur sous-groupe qui ne sont pas encore au courant de toutes les dates. Finalement, le protocole nécessite 2(m-1) appels à la première étape, puis 2 appels à la deuxième étape, puis 2(m-2) appels à la troisième étape, soit au total (4m-4)=2(n-2) appels.

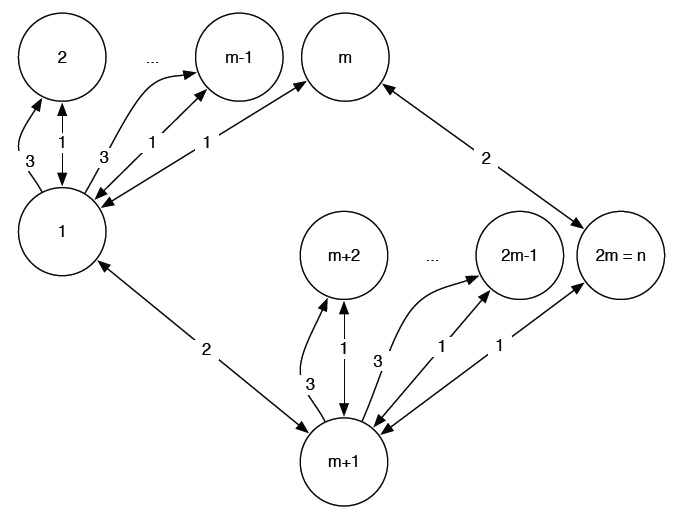
Ce protocole peut être généralisé à des sous-groupes de taille arbitraire et à des nombres impairs d’agents. Dans les années 1970, plusieurs mathématiciens (B. Baker et R. Shostak, R. Tijdeman et A. Hajnal, E. Milner et E. Szemerédi) ont étudié ce problème et ont montré que ces protocoles sont optimaux : il est impossible d’obtenir la connaissance partagée en moins d’appels.

Nous avons élargi ce résultat en définissant un protocole qui produit la connaissance partagée d’ordre k en (k+1)(n-2) appels et nous avons montré l’optimalité de ce protocole (cf. articles en bibliographie). Pour cela, nous avons d’abord dû résoudre un problème conceptuel : comment modéliser les agents, leurs connaissances et la communication de leurs connaissances ? Une solution a été trouvée via un outil classique en Intelligence Artificielle : la logique épistémique.

La logique épistémique

Dans cette logique, une formule comme K_A K_B p exprime que l’agent A sait que l’agent B sait que la proposition p est vraie, et la formule K_A (¬K_B p ∧ ¬K_B ¬p) exprime que A sait que B ignore si p est vraie et que B ignore si p est fausse (où le symbole ¬ est la négation et le symbole ∧ est le « et » logique). Des phrases à propos de la connaissance d’objets comme « Antoine connaît la date de Béa » peuvent alors être exprimées par la disjonction K_Antoine juillet_Béa ∨ K_Antoine août_Béa (où le symbole ∨ est le « ou » logique) c’est-à-dire qu’Antoine sait si Béa est disponible en juillet ou en août. Le langage épistémique permet de définir une forme très générale de la planification épistémique. Tout comme en planification classique, un problème de planification épistémique peut être décrit par la situation initiale, le but, les préconditions et les effets des actions ; mais tandis qu’en planification classique ces ingrédients sont décrits par des formules de la logique classique, ils sont décrits ici par des formules épistémiques. Par exemple, pour deux amis Antoine et Béa qui voudraient respectivement partir en juillet et en août la situation initiale est décrite par la formule épistémique suivante :

K_Antoine juillet_Antoine ∧ K_Béa août_Béa

(Antoine sait qu’il souhaite partir en juillet et Béa sait qu’elle souhaite partir en août).

Le but est d’obtenir la connaissance partagée d’ordre deux, que l’on peut décrire par :

 K_Antoine K_Béa (juillet_Antoine ∧ août_Béa) ∧ K_Béa K_Antoine (juillet_Antoine ∧ août_Béa)

(Antoine sait que Béa sait qu’Antoine est disponible en juillet et Béa en août ; et Béa sait qu’Antoine sait qu’Antoine est disponible en juillet et Béa en août).

Ici nous voyons qu’il s’agit de l’ordre deux car chaque composante de la formule est construite à partir de deux K.

Ceci contraste avec la planification classique où les concepts épistémiques — ici exprimés par les opérateurs K_Antoine et K_Béa —n’interviennent pas : situation initiale, but, préconditions et effets sont décrits par des formules booléennes classiques.

Malheureusement, il a été montré récemment (entre autres par G. Aucher et F. Schwarzentruber de l’IRISA) qu’il n’existe pas d’algorithme pour résoudre tous les problèmes de planification épistémique car c’est un problème indécidable. Afin de simplifier le problème, les chercheurs se sont bornés jusqu’à maintenant à la communication de faits (à travers des formules booléennes), ce qui exclut la communication de connaissances. Nous avons élaboré une approche plus générale permettant la communication de connaissances d’ordre supérieur (c’est-à-dire d’ordre k > 1), ce qui, dans le cas du problème du bavardage décrit précédemment, permet d’atteindre la connaissance partagée d’ordre supérieur.

Par ailleurs, nous avons également réussi à réduire la planification épistémique à la planification classique : on peut transformer le problème d’obtention de la connaissance partagée d’ordre supérieur à partir d’une situation initiale donnée en un problème de planification non-épistémique. Nous avons aussi obtenu d’autres résultats pour des variantes du problème de bavardage, par exemple dans des situations avec plus de contraintes. Ainsi, le graphe de communication peut être non-complet — certains amis ne peuvent pas s’appeler —, ou ce graphe peut inclure des buts d’ignorance — lorsque certains amis ne doivent pas apprendre certaines informations.

La simplicité et la flexibilité du problème du bavardage font de lui un problème basique pour la planification multiagent. Jusqu’à présent, les travaux se sont concentrés sur des solutions centralisées (où un ordonnanceur central détermine l’ordre des appels) mais il est possible d’étudier des variantes distribuées où chaque agent suit son propre protocole. Le nombre minimum d’appels dans le cas centralisé constitue une borne inférieure du nombre d’appels dans le cas distribué. Ce qui montre que les appels seront encore nombreux et que nous pourrons toujours bavarder entre amis.