Jouer ou ne pas jouer au Loto, telle est la stratégie

D’autant que les règles du Loto, créé en France en 1976 et dont les origines remontent à 1933, ont évolué au cours du temps. La combinaison à jouer est ainsi passée de 6 numéros à 5 numéros plus un numéro chance, à cocher sur des grilles de formes variées. De quoi remettre en cause nos stratégies ?

Et que fait un mathématicien dans une telle situation ? Si ses choix ne sont pas ceux de tous, c’est aussi l’occasion de rappeler quelques remarques de bon sens sur le Loto. Pour cela, nous avons consulté Gérard Berry et Jean-Paul Delahaye qui, non sans malice, reviennent sur ce jeu de hasard.

Comment j’ai (mal) joué au Loto

Gérard Berry

Il était une fois, en cette fin de 20^e siècle qui nous paraît déjà si loin, un groupe d’informaticiens et de mathématiciens enflammés par une discussion torride sur un sujet d’importance majeure : faut-il ou non jouer au Loto, c’est-à-dire avoir une probabilité infime de gagner énormément ? Les arguments pour ou contre des uns et des autres défilèrent avec une mauvaise foi confondante, habituelle dans ce type d’assemblée. Au bout de quelques heures, une conclusion s’imposa : aucun argument rationnel définitif ne pouvait être invoqué pour l’une comme pour l’autre des deux alternatives. Cependant, deux propriétés apparurent certaines. Premièrement, si l’on joue des montants suffisamment petits, comparables à ceux qu’on perd avec une régularité métronomique par les trous de ses poches (fréquents chez les informaticiens et les mathématiciens), il n’y a pas de différence observable entre jouer et ne pas jouer. Deuxièmement, comme les gains sont partagés entre les gagnants, il faut se débrouiller pour gagner seul. Donc, il faut choisir une grille dont on est pratiquement certain que les autres ne la joueront pas.

Fort de ces résultats théoriques acquis de haute lutte, je me résolus à passer à la pratique. Lors d’une visite à mon agence bancaire d’Antibes pour retirer de l’argent, j’entrai dans le tabac voisin et demandai à la dame de la caisse une grille de Loto. Avec application, je la remplis soigneusement en cochant de façon bien visible les numéros « 1, 2, 3, 4, 5, 6 ». Lorsque je la lui tendis, elle me regarda comme si j’étais un zombie, me rendit ma grille, et me dit d’un air dégoûté :

—    Monsieur, je refuse de valider votre grille.

—    Mais pourquoi donc ?

—    Parce que les gens ne viennent pas ici pour perdre !

Et, d’un geste péremptoire, elle me montra les photos des gagnants de la région dans les cinq dernières années, qui trônaient fièrement sur un présentoir. N’osant pas lui dire qu’il lui aurait fallu la rue entière pour afficher les morts d’accident de voiture pendant la même période, je lui demandai :

—    Pouvez-vous m’expliquer ?

—    Vous voyez bien que votre grille est complètement déséquilibrée et qu’elle n’a AUCUNE CHANCE ! Six nombres de suite, c’est impossible, surtout ceux-là. En plus, tous les numéros sont sur la même ligne, alors qu’il faut les répartir dans les lignes. Mais pour les colonnes c’est bon, ils sont répartis.

J’ai alors commencé un exercice mental de combinatoire : combien existe-t-il de combinaisons avec un seul numéro par ligne et par colonne ? Mais je n’ai pas eu le temps de faire le calcul, car elle m’a pris par surprise avec la question suivante :

—    Qu’est-ce que vous faites comme métier ?

Je n’allais pas lui dire que j’étais informaticien, métier encore inconnu du public. Mais je pensais l’impressionner avec une réponse quand même un peu vraie :

—    Je suis mathématicien.

—    Ah, ça explique tout ! Raison de plus de ne pas valider votre ticket !

La discussion avait attiré les autres consommateurs, heureux d’une part d’avoir un cours de Loto gratuit et d’autre part de voir un mathématicien se faire remettre à sa place (vengeance liée à de mauvais souvenirs d’école, je présume). Ils commençaient à me regarder comme si j’étais un poisson avarié. Je compris qu’il était temps de partir.

Je repris ma voiture, entrai dans un hypermarché où il y avait aussi un bureau de Loto avec les mêmes photos de gagnants. La buraliste y valida ma grille d’un air totalement indifférent.

Bien sûr, je perdis.

Une semaine après, au laboratoire d’informatique parisien où j’étais allé faire un cours, nous devisions gaiement avec les chercheurs locaux autour d’un café. Je racontai mon histoire, qui fit beaucoup rire mes collègues, sauf un qui me dit avec tristesse :

—    Toi aussi, tu joues « 1, 2, 3, 4, 5, 6 » ?

Je garantis que cette histoire est vraie, et à peine arrangée (je vis au sud de la Loire quand même). Elle est d’ailleurs bien trop belle pour que j’aie pu l’inventer !

Du bon sens probabiliste…

Jean-Paul Delahaye

Concernant le Loto, qui a connu diverses variantes depuis qu’il est proposé par la Française des jeux, le bon sens probabiliste indique quelques vérités qu’il ne faut jamais oublier.

–A– Si les roues qui permettent de mener les tirages ne sont pas truquées (et personne ne pense sérieusement qu’elles sont truquées) alors toutes les combinaisons ont la même chance d’être tirées et donc une grille avec 1, 2, 3, 4, 5 n’est pas plus absurde qu’une grille équilibrée. Équilibrer ses choix sur la grille est inutile pour augmenter ses chances de gagner.

–B– Si les roues qui permettent de mener les tirages ne sont pas truquées, alors les tirages des semaines ou des années précédentes n’ont aucune influence sur le prochain tirage. Il est donc inutile de collecter les tirages passés et d’en tenir compte en croyant augmenter les chances de gagner de sa grille. Joseph Bertrand écrivait : « on fait trop d’honneur à la roulette : elle n’a ni conscience ni mémoire ».

–C– La Française des jeux ne redistribue qu’environ 50% des sommes jouées. Que l’on joue au hasard ou avec une quelconque méthode (prenant par exemple en compte les derniers tirages) on perd donc statistiquement à peu près la moitié de l’argent qu’on mise. Mieux vaut aller dans les casinos qui redistribuent proportionnellement une plus grande partie de l’argent joué.

–D– Reste que les sommes distribuées au Loto le sont entre ceux qui ont gagné, qui peuvent être plus ou moins nombreux à se partager les gains. Il est donc souhaitable d’être aussi peu nombreux que possible à avoir joué la grille gagnante. Il faut donc jouer des combinaisons de numéros qui sont peu jouées ; cela n’augmente pas les chances de gagner, mais cela augmente la somme gagnée quand on gagne.

–E– Par ailleurs, contrairement à ce qu’on pense, jouer 1, 2, 3, 4, 5 est une combinaison souvent jouée, et l’histoire racontée le montre encore une fois. Sur cet aspect, voir l’article paru dans Pour la Science Les lecteurs ne jouent pas au hasard.

Au sujet des numéros joués par les joueurs humains, des études statistiques ont été menées (voir Lotos et loteries). Elles ont montré (selon deux méthodes qui se recoupent) que le 7 est le numéro le plus joué, que le 41 est le numéro le moins joué, et plus généralement que la probabilité qu’un numéro soit joué est donnée par la courbe suivante, tirée du livre de Patrick Roger Lotomania : une approche scientifique du jeu et du comportement des joueurs, Éditions Village Mondial, Pearson Éducation France, 2005.

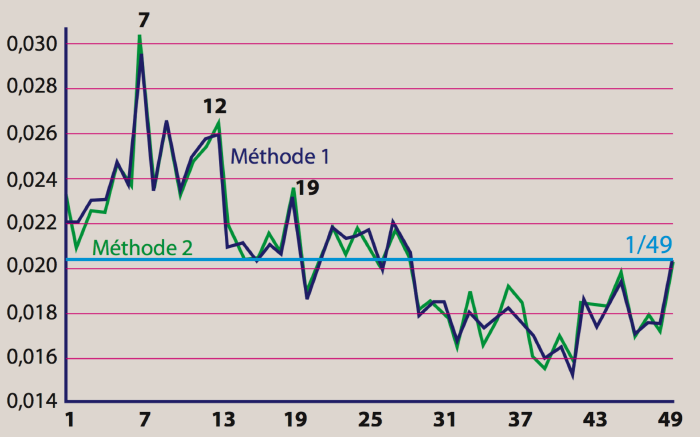
Une autre conclusion de ces études est que parmi les combinaisons les moins jouées, il y a  32-38-39-40-41-43.

Cette combinaison serait donc plus rentable que la plupart des autres (sauf si les joueurs lisant ce texte ou un autre texte qui la mentionne se mettent à la jouer). Cependant, même en la jouant, l’espérance de gain pour 100 euros joués restera largement inférieure à 100 euros (à cause de la faible redistribution des sommes jouées). Finalement, à ce jeu, aucune méthode ne peut ramener votre espérance de gain au niveau des sommes que vous engagez : si vous ne voulez pas perdre, il ne faut pas jouer.