Analyser les génomes des océans

Qui est Tara ?

La goélette Tara. Photo © Yohann.cordelle [CC BY 3.0], via Wikimedia Commons.

Tara, c’est avant tout un magnifique voilier, une goélette de 36 mètres, propulsée par 400 m² de voilure. Elle a appartenu successivement à Jean-Louis Étienne puis à Sir Peter Blake, avant qu’Étienne Bourgois, directeur général de la marque agnès b., ne l’acquière pour la transformer en un formidable outil d’étude des océans et de sensibilisation du grand public.

Les diverses expéditions de Tara sont entre autres motivées par l’étude du plancton, ces organismes vivant dans l’eau et qui se déplacent au gré des courants. Nous connaissons encore bien peu de choses sur les espèces qui le composent, allant de petits animaux jusqu’aux bactéries et aux virus. Et pourtant, le plancton représente 98 % du volume de toutes les espèces animales marines confondues, il est à la base de la chaîne alimentaire et à l’origine de plus de 50 % de l’air que nous respirons. Ainsi la survie ou l’évolution du plancton au regard des changements climatiques conditionnent la survie des organismes vivants sur notre planète, humains inclus. Rien que ça.

Depuis 2009, Tara sillonne les océans du globe. À bord, à l’aide de filtres, les scientifiques « pêchent » du plancton à différentes positions géographiques. Pour chacune de ces positions, un prélèvement du plancton est effectué à diverses profondeurs et pour différents filtres de tailles d’individus.

Une fois ces prélèvements effectués, le but est de lire leurs génomes. C’est une étape clé pour étudier la diversité. C’est aussi indispensable pour comprendre les mécanismes d’adaptation des espèces face aux changements environnementaux tels que le réchauffement climatique.

Accéder à l’intimité de l’ADN : le séquençage

Les échantillons collectés sont envoyés au Genoscope, le centre national de séquençage français. Sur place, l’ADN de chaque échantillon est extrait, avant d’être analysé par des séquenceurs. Comme nous l’avons déjà évoqué ici et là, les séquenceurs sont des machines conçues pour lire le contenu des molécules d’ADN, à partir desquelles ils produisent des fichiers textes utilisant uniquement l’alphabet A, C, G et T. Ces suites de lettres correspondent à l’enchaînement des nucléotides constituant les molécules d’ADN et qui sont porteurs de l’information génétique.

Rappelons que le résultat du séquençage d’une molécule d’ADN n’est pas une séquence textuelle comportant autant de lettres que la molécule ne comporte de nucléotides. En effet, en raison de limitations à la fois sur le plan de la biologie et de la technologie de séquençage, les séquenceurs génèrent de courtes séquences de quelques centaines ou milliers de lettres, mais ils en génèrent beaucoup. Ainsi, lorsqu’il s’agit de séquencer le génome d’une espèce, un séquenceur peut produire plusieurs dizaines de millions de ces courtes séquences, que l’on appelle les « lectures » (des « reads » en anglais). Chacune de ces lectures provient d’une position sur le génome. Malheureusement, lors du séquençage, la position de chaque lecture sur le génome est perdue. Ajoutons à cela le fait que l’ADN est composé d’une double hélice formée de deux brins, et que le processus de séquençage ne permet pas de connaître le brin d’où provient chaque lecture. Et pour corser le tout, le séquençage n’est pas parfait, les lectures comportent des erreurs, des lettres peuvent être fausses, supprimées ou ajoutées.

Les plus grands puzzles du monde

Si l’on souhaite reconstruire le génome d’une espèce séquencée, nous utilisons le fait que ses lectures se chevauchent. À l’image de deux pièces d’un puzzle, deux lectures qui se chevauchent peuvent être assemblées en une lecture plus grande.

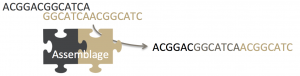
De proche en proche ce processus peut permettre de reconstruire la séquence complète de la molécule d’ADN. Cette étape, appelée l’assemblage, consiste donc à « jouer au puzzle ». Il s’agirait d’un puzzle de plusieurs dizaines de millions de pièces, qui ne s’emboîteraient pas toujours à la perfection en raison des erreurs, et qui seraient imprimées sur leurs deux faces dont seule l’une d’entre elles serait la bonne. L’angoisse.

Dans le cas des données Tara, nous ne séquençons pas un génome unique, mais l’ensemble des génomes qui composent chaque échantillon. En effet, le contenu d’un échantillon ne se limite pas à une espèce, loin de là. Un litre d’eau de mer peut contenir plusieurs dizaines de millions d’espèces différentes. À l’issue du séquençage d’un tel échantillon, il est impossible de connaître de quelle espèce est issue chaque lecture. Ainsi, nous pouvons considérer le résultat du séquençage d’un échantillon Tara comme une partie des pièces de millions de puzzles mélangées dans une grande boîte contenant plusieurs centaines de millions de pièces. Globalement, une telle boîte de pièces, autrement dit le mélange des lectures de toutes espèces séquencées à partir d’un milieu (eau, air, sol, …) est appelé un métagénome.

En pratique, du point de vue de l’informaticien, un métagénome est donc un fichier texte, comportant quelques centaines de millions de lectures, chacune composée d’environ cent caractères sur l’alphabet A,C,G,T.

En ce qui concerne les données issues du projet Tara, une difficulté supplémentaire vient du fait qu’il n’y a pas qu’un seul métagénome, mais un par échantillon, c’est-à-dire environ 2400 métagénomes, donc plus de 2400 boîtes distinctes. On prend alors conscience du défi auquel nous devons faire face pour extraire de l’information biologique pertinente de ces données, comportant au final environ 330 milliards de pièces de puzzle, c’est-à-dire 330 milliards de lectures, d’une centaine de caractères chacune.

Que faire de ces données ?

Disons-le tout de suite, l’assemblage de métagénomes aussi complexes que ceux issus du plancton reste aujourd’hui hors de portée, même si les technologies de séquençage évoluent rapidement et permettent la génération de lectures de plus en plus longues (des puzzles composés de moins de pièces mais plus grosses).

Plutôt que de les assembler, nous pouvons aussi imaginer comparer chacune des lectures aux génomes individuels déjà correctement assemblés et connus. Malheureusement, cette opération pourtant classique pour analyser des données de séquençage s’avère peu fructueuse lorsqu’il s’agit des données générées par Tara. En effet, moins de 10 % des lectures sont similaires à des espèces connues, soulignant à quel point la connaissance sur le plancton est limitée. Malgré son intérêt, cette comparaison aux génomes connus laisse donc de côté plus de 90 % des données, soit un véritable trésor…

Donc on ne peut rien faire ?

En résumé, les données de séquençage du plancton échantillonné grâce à Tara ne peuvent pas être assemblées et leur comparaison avec les espèces déjà connues est trop limitée. La situation semble désespérée, mais il reste un espoir d’extraire de l’information de ces jeux de données  en les comparant les uns aux autres. Imaginons que l’on soit capable de dire simplement quels métagénomes sont les plus similaires et lesquels sont les plus différents ; ou plus généralement que l’on soit capable d’associer un score de similarité entre toutes les paires des métagénomes. Avec une telle information, nous serions alors en mesure de mettre en relation cette similarité en terme de contenu génomique avec d’autres mesures liées à la position géographique ou à différents paramètres tels que l’acidité ou la température ou encore à des phénomènes locaux comme la remontée en surface des eaux profondes.

Ainsi, entre deux métagénomes, nous souhaitons pouvoir attribuer un score de similarité entre 0 (totalement différents) et 1 (parfaitement identiques). Facile, il suffit de savoir pour chaque lecture du premier métagénome s’il existe dans le second une lecture qui lui est similaire. Ensuite on combine le résultat pour toutes les lectures et on en dérive une mesure globale de similarité entre les deux métagénomes.

Comparer une séquence à une autre est une opération classique pour laquelle il existe des méthodes exactes basées sur la programmation dynamique (dont nous avons parlé ici) ou des méthodes approchées telles que BLAST développée au National Center for Biotechnology Information aux États-Unis. Cependant, en supposant que l’on soit très optimiste et que l’on puisse comparer deux lectures en 0.0000001 seconde, et en sachant que les deux métagénomes à comparer sont composés d’environ 100 millions de lectures chacun, alors, pour comparer deux métagénomes, il faudrait effectuer 100 millions x 100 millions de comparaisons. Ceci nécessiterait 0.0000001 x (100 x 10⁶)² secondes, autrement dit, 32 années de calcul (sans coupure de courant !). Et nous ne parlons ici que de deux métagénomes. Si nous souhaitons comparer deux à deux tous les 2400 métagénomes issus du projet Tara, il faudrait donc 32 x 2400² années, autrement dit plus de 180 millions de siècles de calculs.

Donc on ne peut vraiment rien faire ?

Au regard des masses de données à prendre en compte et à la lumière du calcul précédent, il semble évident que pour comparer deux métagénomes, il est impossible de proposer en un temps raisonnable une approche qui nécessiterait de comparer toutes les paires de lectures possible. Nous devrons donc nous contenter d’une solution moins raffinée mais toutefois suffisamment informative. C’est la démarche adoptée par l’équipe de recherche GenScale qui a développé le logiciel Simka.

Pour développer ce logiciel, l’idée fondamentale suivante a été exploitée. Si deux séquences sont similaires, alors elles partagent exactement des sous-séquences de taille fixée k que nous appellerons des « k-mers ». Par exemple, considérons les séquences « ACCAGATCCTGT » et « AGCTGATCCTAT ». Ces deux séquences sont identiques à trois substitutions près, comme on peut le voir dans l’alignement suivant :

ACCAGATCCTGT
|.|.||||||.|
AGCTGATCCTAT 

Nous pouvons constater que ces deux séquences partagent exactement deux 5-mers : « GATCC » en position 4 et « ATCCT » en position 5 (rien n’interdit à ces k-mers de se chevaucher) !

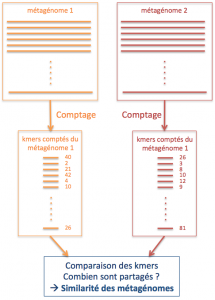
Inversement, en moyenne, deux séquences qui partagent « beaucoup » de k-mers sont plus similaires que deux séquences qui partagent pas ou peu de k-mers. Ainsi la similarité de deux séquences peut être estimée par le nombre de k-mers qu’elles ont en commun. Or, d’un point de vue informatique, effectuer un tel comptage est largement plus simple et plus rapide que d’aligner les séquences comme nous l’avons fait dans l’exemple précédent. Le cœur de l’algorithme de Simka est basé sur cette idée cruciale.

Nous avons évoqué plus haut qu’il paraît impossible de comparer toutes les paires de lectures de deux jeux de données : k-mers ou pas k-mers, ceci reste vrai. Qu’à cela ne tienne, puisque la comparaison de toutes les paires de séquences n’est pas envisageable, alors pour comparer deux métagénomes, nous nous limitons à comparer globalement leur contenu en k-mers.

Pour bien dormir, comptons quelques centaines de milliards de k-mers

Nous avons largement simplifié le problème. Pour trouver une mesure de similarité entre deux métagénomes, nous ne comparons pas des paires de lectures entre elles, mais nous estimons globalement la similarité en comptant le nombre de mots de taille k (les k-mers) que partage la totalité des lectures de chaque métagénome.

Les problèmes ne sont pas terminés pour autant. Pour comparer deux métagénomes, il est nécessaire de connaître le contenu en k-mers de chacun d’entre eux. Ainsi il faut une méthode capable d’extraire tous les k-mers distincts d’un jeu de lectures et de les compter, pour pouvoir ensuite les comparer à d’autres jeux de lectures. Par exemple, pour le jeu suivant comportant deux lectures :

GGACTCG et
CACTCGA

avec k = 5, nous aurions les 5-mers suivants, associés à leur abondance :

GGACT 1
GACTC 1
ACTCG 2
CACTC 1
CTCGA 1

La solution semble toute simple pour effectuer ce comptage : on peut créer un tableau comportant 4^k cases (tous les k-mers possibles avec un alphabet de quatre lettres) qui associe chaque k-mer à son nombre d’occurrences, et incrémenter le nombre d’occurrences d’un k-mer lorsqu’il est vu dans les lectures. Cette solution est acceptable lorsque l’on utilise une petite valeur de k comme dans l’exemple précédent. Cependant, nous utilisons en pratique des valeurs de k autour de 30. Or, un tableau de 4³⁰ valeurs entières nécessiterait un espace de stockage de 1024 pétaoctets, c’est-à-dire plus d’un million de téraoctets, en gros l’équivalent de deux millions de disques durs d’ordinateurs personnels (et il faudrait ça pour chacun des 2400 métagénomes).

Une autre solution, basée sur une structure de données classique du type table de hachage pourrait sembler acceptable, mais là encore la désillusion est de taille (sans jeu de mots). Un métagénome marin contient environ 10 milliards de k-mers différents, les stocker avec leur abondance pour les 2400 jeux de données dans une telle table nécessite pas loin de 24 téraoctets de mémoire, ce qui n’est pas non plus acceptable.

Quand la RAM rame le disque dure

Alors quelle est la solution implémentée dans le logiciel Simka ? L’idée est assez simple. Elle consiste, pour chaque métagénome, à écrire tous les k-mers d’un jeu de données dans un fichier sur le disque dur. Une fois cette opération effectuée, les k-mers de ce fichier sont triés dans l’ordre alphabétique. Cette opération est très optimisée et peut être effectuée rapidement. Ainsi, si un k-mer apparaît plusieurs fois dans un jeu de données, alors il apparaît sur plusieurs lignes consécutives dans le fichier des k-mers trié, il est donc facile de compter le nombre d’occurrences de chaque k-mer à partir d’un tel fichier trié.

Par exemple, si l’on reprend nos séquences GGACTCG et CACTCGA, le fichier de k-mers bruts (avec k = 5) serait :

GGACT
GACTC
ACTCG
CACTC
ACTCG
CTCGA

Le fichier de k-mers trié serait alors :

ACTCG
ACTCG
CACTC
CTCGA
GACTC
GGACT

En lisant ce fichier de haut en bas, on déduit que tous les k-mers sont vus une fois, à l’exception de ACTCG qui a deux occurrences.

Le tri des k-mers apporte un second avantage. Supposons que l’on souhaite maintenant comparer les k-mers de deux jeux de données, alors il suffit de lire de haut en bas de manière simultanée les deux fichiers de k-mers triés. On peut alors en déduire non seulement quels sont les k-mers partagés, mais aussi l’abondance de leur partage.

Mieux, si l’on souhaite comparer plus de deux métagénomes, il est également facile de lire simultanément tous les fichiers de k-mers triés de tous les jeux de lectures de ces métagénomes.

Cette fois-ci, c’est gagné, on utilise le disque plutôt que la mémoire et on répond à la question.

Sans entrer dans les détails d’implémentation, une dernière précision : plutôt que de créer un énorme fichier unique de k-mers par métagénome, on regroupe les k-mers par paquets et on crée un fichier par paquet et par métagénome. Par exemple, pour chaque métagénome, tous les k-mers qui débutent par AA sont dans un paquet, tous ceux qui débutent par AC sont dans un autre paquet, etc. Ceci permet de diviser le travail en plus petites tâches, de faciliter le tri de chaque fichier, et de paralléliser facilement les calculs.

Et on peut vraiment traiter de grosses masses de données ?

Simka a été testé sur un jeu de données publiques comportant 690 métagénomes issus de microbiotes intestinaux humains. Le microbiote intestinal, également appelé flore intestinale, est l’ensemble de bactéries, virus, parasites et champignons non pathogènes que contient notre système digestif. D’importantes découvertes sont en cours sur le lien entre le contenu du microbiote intestinal et diverses maladies.

Le choix de tester Simka sur ces données plutôt que sur celles de Tara vient simplement du fait que les données Tara n’étaient pas encore publiques à l’heure de la publication de l’outil, tandis que les données du microbiote permettaient de tester l’efficacité de Simka en termes de puissance de calcul et de précision de ses résultats. Ce jeu de données comporte 32 milliards de lectures composées de plus de 2300 milliards de k-mers différents (avec k = 31). Simka a nécessité trois jours de calculs et a utilisé 800 gigaoctets de disque et 62 gigaoctets de mémoire pour effectuer toutes les comparaisons deux à deux de tous les jeux de données. Cela peut sembler gros, mais ce type de ressources est aujourd’hui facilement accessible via de nombreux centres de calculs.

Faire parler les océans

Sur les données Tara, une étude en cours exploite les résultats obtenus grâce au logiciel Simka. Sur les métagénomes issus de la Méditerranée ainsi que des océans Atlantique et Pacifique, la mesure de similarité obtenue à partir de tous les échantillons (2400 métagénomes pour environ 330 milliards de lectures) a permis de définir des « provinces génomiques ». Une province génomique est une zone géographique de taille variable allant de l’archipel océanique jusqu’à plusieurs océans et regroupe un ensemble d’organismes planctoniques qui partagent une similarité du point de vue du contenu en génomes.

Ces grandes zones géographiques sont différentes selon la taille des organismes étudiés, ce qui permet d’émettre des hypothèses quant à l’adaptation du plancton en fonction de sa taille et de son environnement (salinité, acidité, température, etc.).

Nous disposons par ailleurs de modèles permettant d’anticiper les modifications de ces conditions environnementales au regard du changement climatique. Ainsi nous pouvons anticiper les modifications géographiques des provinces génomiques, leurs déplacements, leurs réductions ou leurs expansions, avec les conséquences que ceci pourrait avoir sur la population des océans, et sur toute la chaîne alimentaire, l’humain compris.