Naviguer comme les Polynésiens

À l’heure de la robotique mobile et de l’intelligence artificielle, on se demande souvent comment doit réagir le véhicule autonome en cas d’obstacle imprévu ou de défaillance d’un capteur. Mais pour de tels robots, on imagine un environnement structuré avec des routes, des trottoirs, des règles de circulation.

Le problème est d’une autre nature lorsque l’on considère l’exploration par des robots autonomes d’un environnement non structuré. Il peut s’agir d’une planète lointaine, d’une grotte jamais visitée, de structures karstiques inexplorées (comme des rivières souterraines) ou des fonds marins. Dans un tel contexte, où aucun moyen de localisation n’existe, où la téléopération (opération à distance) est impossible, le robot doit explorer sans se perdre. Parfois il doit même construire une carte de l’environnement afin de se déplacer de façon déterministe et efficace, ceci dans le but d’accomplir la mission demandée. Nous parlerons de robotique d’exploration.

Cet article se décompose en deux parties. La première partie concerne la navigation. Elle montre comment il est possible de se déplacer dans un environnement non structuré, vaste, mais relativement connu. Nous insisterons sur l’importance de la notion de chemin qui permet de se déplacer d’un point à un autre sans se perdre et sans pour autant disposer d’une carte ou même de système de géolocalisation. Nous nous appuierons sur les méthodes de navigation des Polynésiens, afin d’illustrer les concepts introduits. Nous aurions également pu faire référence à d’autres types de grands navigateurs tels que les pigeons, les tortues marines ou autres animaux migrateurs. Dans la deuxième partie, nous discuterons d’exploration. Il ne s’agit plus alors de naviguer dans un environnement connu, mais aussi d’agrandir la partie connue du monde sans prendre le risque de se perdre.

Dans cet article, et sans trop entrer dans les détails, nous parlerons également d’équations différentielles pour représenter le mouvement du navigateur et de théorie des ensembles pour la représentation des zones connues ou à explorer. Ces outils sont utilisés par les ordinateurs implantés dans les robots autonomes d’exploration afin de représenter la connaissance de leur monde, construire la carte de leur environnement, comprendre leur propre comportement et calculer les déplacements futurs à effectuer pour atteindre l’objectif de la mission.

La navigation dans un environnement non structuré

La navigation moderne repose sur la notion de géolocalisation et de carte métrique. Cette géolocalisation est rendue facile grâce au GNSS (Global Navigation Satellite System) comme le GPS ou Galiléo. Si le navigateur ne sait pas se positionner sur la carte, il considère qu’il est perdu.

Dans des temps plus lointains, cette notion de géolocalisation était moins naturelle et on procédait alors à d’autres approches dites topologiques, qui sont maintenant reprises dans un contexte de robotique mobile dans des environnements non structurés, sans accès au GPS. Avant de définir plus précisément ces approches, donnons ci-dessous quelques exemples de navigation topologique dans différents contextes.

Sur terre. Pour se déplacer, le voyageur (ici un marcheur) peut disposer d’un algorithme lui permettant de trouver un chemin pour aller d’un point A (un village par exemple) à un point B (un autre village). Un tel chemin peut correspondre à : « Partant de A, remonter la rivière ; au deuxième pont, prendre à droite puis longer la forêt jusqu’à voir le clocher de l’église B ». Le marcheur sait qu’en suivant un tel chemin, il arrivera à destination, mais ne sait pas précisément quand. Il ne sait pas se localiser, mais n’est pas perdu car il peut rejoindre sa destination et revenir.

Sur la mer. Les Polynésiens se déplaçaient dans l’océan Pacifique sur des voiliers de type catamaran, des wa’a kaulua. Ils ne disposaient ni de GPS, ni de boussoles, ni d’horloges. Ils étaient capables de se déplacer d’une île à l’autre en suivant des chemins : des chemins d’étoiles. Comme illustré par la figure 1 ci-dessous, l’environnement de navigation est gigantesque, les îles sont rares et petites, les bateaux ont une évolution incertaine qui dépend des vents et des vagues.

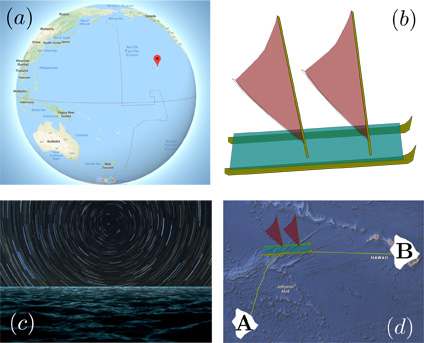
Fig. 1. (a) Retrouver Hawaï dans l’Océan Pacifique ; (b) Wa’a kaulua ; (c) Les étoiles tournent autour d’un même point (Étoile Polaire ou Croix du Sud) ; (d) Le navigateur contrôle son bateau pour rester à la bonne latitude.

Prenons l’exemple d’un navigateur polynésien voulant rejoindre une petite île B située à une semaine de navigation au nord-est de l’île A où il se trouve, comme illustré par la sous-figure 1(d). Il sait que sur cette île B, l’étoile α se lève lorsque l’étoile β se couche (voir figure 2 ci-dessous). Si sur son trajet, il observe le même phénomène, c’est qu’il est à la latitude de l’île B, avec une précision de l’ordre de 50 km. Il peut donc facilement rejoindre le parallèle correspondant à l’île B et s’y tenir. Il rencontrera l’île B si les conditions météorologiques sont bonnes et si l’île B n’est pas trop petite. Notons que les étoiles sont également utilisées pour la mesure du cap, en remplacement de la boussole.

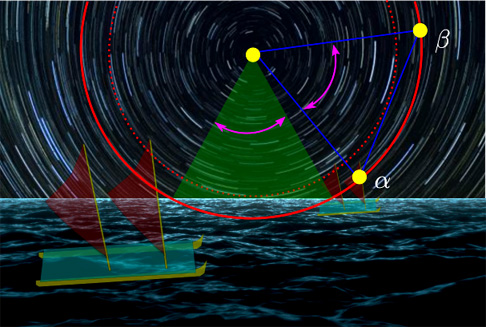
Fig. 2. La paire d’étoiles α et β correspond à une latitude précise : celle de l’île que nous cherchons à rejoindre. Nous sommes à la bonne latitude si α se lève lorsque β se couche.

Sous l’eau. Sous l’eau, la vision stellaire n’est pas possible. En revanche, on connaît facilement sa profondeur grâce à un capteur de pression. On peut suivre des chemins équivalents à celui formé par les étoiles pour le navigateur polynésien ou par la rivière pour le voyageur terrestre. Ces chemins peuvent correspondre par exemple :

• à un front isotherme (cette technique est utilisée par les animaux marins, comme les tortues) ;
• à un chemin magnétique (comme celui suivi par les pigeons pour rejoindre leur pigeonnier) ;
• à un parallèle. Les gyroscopes peuvent ressentir la rotation de la Terre et l’angle formé avec la verticale nous permet de retrouver la latitude ;
• à une isobathe. Le robot sous-marin se régule relativement à une courbe de niveau sous-marine (une isobathe). Il lui faut pour cela un écho-sondeur pour mesurer la distance au fond (voir figure 3 ci-dessous).
  
  

  Fig. 3. Un robot sous-marin (trace en bleu) peut suivre indéfiniment une isobathe, sans jamais refaire surface. Les projections sur la surface et sur le fond sont également représentées.

Navigation topologique. Que cela soit sur terre ou sur l’eau, on navigue dans un monde que l’on peut considérer comme bidimensionnel, c’est-à-dire comme une surface sur laquelle nous pouvons marcher, rouler, etc. La navigation topologique repose sur le principe suivant. On mesure une grandeur scalaire \(V(\mathbf{p})\) qui dépend de notre position \(\mathbf{p}\) sur le plan. Cette grandeur peut correspondre au temps écoulé entre le lever de l’étoile α et le coucher de β, ou à la distance à la côte, à la température de l’eau, à l’amplitude du champ magnétique terrestre, etc. Le navigateur cherchera à se réguler relativement à une valeur de référence \(\bar{V}\) correspondant à la cible B. La courbe d’équation \(V(\mathbf{p})=\bar{V}\) correspond à un chemin \(\mathcal{C}\) qui lui permettra de rejoindre la cible. Dans le cas où le véhicule évolue dans un monde tridimensionnel (dans les airs par exemple), nous avons besoin de deux fonctions \(V_{1}(\mathbf{p}),V_{2}(\mathbf{p})\) et de deux valeurs de référence \(\bar{V}_{1},\bar{V}_{2}\) pour définir ce chemin \(\mathcal{C}\). Il restera alors au pilote (le navigateur ou le régulateur dans le cas d’un robot) à manœuvrer de façon à rejoindre le chemin \(\mathcal{C}\) et le suivre jusqu’à la cible B. Les tortues marines, les pigeons, les navigateurs polynésiens utilisent ce principe pour naviguer sans se perdre.

Dans le cas d’un robot, la théorie du contrôle s’intéresse à comment agir sur les différents actionneurs (gouvernes, propulseurs, volant, réglages des voiles, etc) par un algorithme de régulation de façon à rejoindre le chemin désiré. Cette théorie n’est pas développée ici mais est abordée dans le livre La Robotique Mobile, Cours et Exercices ou le MOOC RobMOOC.

Carte. Un amer est un point remarquable de l’espace. En navigation moderne, un amer est positionné sur une carte métrique et permet une géolocalisation du navigateur. En navigation topologique, un amer permet un changement de stratégie dans la navigation. Dans l’exemple du marcheur, lorsqu’une partie du chemin est décrite par « au deuxième pont, prendre à droite », le pont est un amer qui n’est pas géolocalisé. Dans un environnement sans amers remarquables, l’intersection entre des courbes iso-valeurs \(\left(V_{i}(\mathbf{p})-\bar{V_{i}}=0\right)\) définit un amer ponctuel que l’on peut retrouver et sur lequel nous pouvons nous baser pour changer de stratégie de navigation. En changeant de stratégie aux amers rencontrés, le navigateur peut se déplacer en parcourant un cycle, sans se perdre, même s’il ne connaît pas son monde. Un petit exemple est illustré par la figure 4 ci-dessous où un robot sous-marin parcourt un cycle. La stratégie de navigation utilisée par le robot est donnée par l’algorithme suivant.

1. Suivre l’isobathe 50 mètres jusqu’à la rencontre de l’isotherme à 15 degrés
2. Suivre l’isotherme à 15 degrés, jusqu’à la rencontre de l’isobathe 50 mètres
3. Aller à l’étape 1

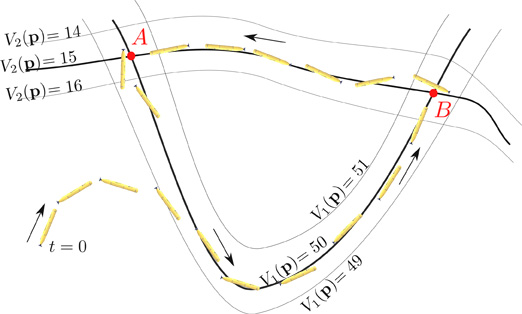
Fig. 4. Le robot alterne entre un suivi d’isobathe et un suivi d’isotherme, effectuant ainsi un cycle.

La carte qui correspond à la représentation que possède le robot de cet environnement n’est plus de nature métrique et est dite topologique. Une carte topologique est un diagramme simplifié qui ne comprend que les informations vitales pour la navigation, un peu comme le plan du métro parisien qui permet de se rendre d’une station à l’autre en identifiant les changements à effectuer. Ce type de carte ne représente pas les distances, mais les relations entre les amers (les stations de métro) avec une information pour naviguer d’un amer à l’autre. La figure 5 ci-dessous représente une carte topologique du cycle évoqué à la figure 4. Cette carte est analogue à une carte de métro avec deux stations A et B et deux lignes.

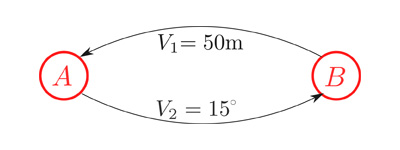
Fig. 5. Carte topologique permettant de réaliser un cycle.

Nous venons de proposer une approche programmable permettant à un navigateur ou à un robot de se déplacer dans un environnement naturel, comme celui des Polynésiens qui ne disposaient pas d’amers remarquables dans leur environnement. Cette stratégie, qui s’appuie sur une carte topologique de l’environnement, permet de suivre un chemin ou un cycle sans jamais se perdre. Au cours de l’évolution des espèces, les animaux marins ont développé de telles stratégies pour suivre des cycles. Par exemple, les tortues marines suivent des cycles reproductifs qui leur imposent un retour à leur lieu de naissance pour pondre. En revanche, le navigateur polynésien doit trouver ses chemins ou cycles par ses propres moyens. C’est le rôle de l’exploration que nous allons voir dans la prochaine section. L’exploration est un problème difficile qui requiert une approche métrique. Pour explorer, le navigateur cherchera à construire une carte qu’il utilisera pour la localisation.

L’exploration d’un environnement inconnu

Pour maîtriser sa navigation, il est important de savoir construire une carte, qu’elle soit topologique ou métrique. Rappelons qu’une carte est métrique si on peut l’utiliser pour évaluer des distances alors qu’une carte est topologique si on peut l’utiliser pour se déplacer, comme la carte du métro parisien qui nous renseigne sur les lignes à prendre pour arriver à la destination souhaitée.

Pour construire une telle carte, il faut être capable d’explorer un environnement inconnu sans se perdre. Cette étape d’exploration a dû être faite par les navigateurs polynésiens afin de pouvoir découvrir de nouvelles îles, puis d’y amener leur famille, animaux domestiques et plantes cultivées. Cette étape doit se faire en garantissant que l’explorateur ne se perdra pas.

Nous allons ici nous placer dans le cadre des navigateurs polynésiens, mais il faut imaginer derrière cela un ou des navigateurs, marcheurs, robots sous-marins… évoluant dans un environnement avec des amers (des îles, des câbles sous-marins, un lac), sans possibilité de voir des étoiles ou autre grandeur scalaire permettant de construire des chemins.

Pour fixer les idées, le monde dans lequel nous nous plaçons est un océan, avec un ciel sans étoiles et comprenant quelques rares îles distantes les unes des autres. Dans cet océan, les seuls amers sont les îles elles-mêmes. Pour simplifier, nous allons supposer que si une île connue est en vue, le navigateur est capable de l’explorer et de savoir où il se trouve relativement à cette île. Il sait également la placer sur une carte métrique. Cette hypothèse de ciel sans étoiles peut sembler surprenante dans le cas des Polynésiens, mais nous la prenons délibérément pour éviter que des concepts trop différents s’entremêlent. De plus, elle se justifie dans le cas de la navigation sous-marine.

Dynamique

Supposons l’océan sans île. Le navigateur sait où il se trouve à l’instant \(t=0\), un peu comme s’il avait un GPS juste à cet instant initial. Il a une idée approximative de sa vitesse, de sa rotation… Il sait en gros comment il bouge. Cette connaissance grossière de sa dynamique peut être décrite mathématiquement par une équation différentielle de la forme :

\[ \left\{ \begin{array}{cc} \dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right),~ & \mathbf{u}\left(t\right)\in\mathbb{U}\left(t\right)\\ \mathbf{x}\left(0\right)=\mathbf{x}_{0} \end{array}\right. \]

où :

• \(t\) est le temps
• \(\mathbf{x}(t)\) est le vecteur d’état (position, cap, vitesse)
• \(\dot{\mathbf{x}}(t)\) est la dérivée de \(\mathbf{x}(t)\) par rapport au temps
• \(\mathbf{u}(t)\) est l’entrée du système (gouvernail, réglage de voile) qui peut être choisie par le navigateur avec plus où moins d’imprécision
• \(\mathbf{f}\) est la fonction d’évolution qui est obtenue par l’application des lois de la physique, comme par exemple le principe fondamental de la dynamique
• \(\mathbf{x}_{0}\) est la condition initiale.

Cette équation nous permet de prédire, grâce aux lois de la physique, comment va évoluer le vecteur d’état du système en fonction du temps. L’entrée \(\mathbf{u}(t)\) est connue approximativement : elle est censée appartenir à un ensemble \(\mathbb{U}\) connu. Ce qu’il faut retenir, c’est que pour une condition initiale \(\mathbf{x}_{0}\), il existe plusieurs trajectoires compatibles avec notre dynamique et que c’est ce que décrit cette équation différentielle. Dans ce qui suit, pour simplifier, nous allons supposer que le vecteur d’état \(\mathbf{x}=(x_{1},x_{2})\) correspond à la position du robot, alors que dans le cas général \(\mathbf{x}\) est de plus grande dimension et contient également les grandeurs du système qui varient avec le temps, comme la vitesse ou le cap.

On définit le flot \(\boldsymbol{\Phi}(t_{1},\mathbf{x}_{0})\) associé à un état initial \(\mathbf{x}_{0}\) pour un temps \(t_{1}\) comme l’ensemble des états atteignables à l’instant \(t_{1}\) en partant de \(\mathbf{x}_{0}\). Il s’agit d’un terme mathématique associé à n’importe quelle équation différentielle et pas à un terme technique lié à notre problème d’exploration. On peut écrire le flot sous une forme mathématique comme suit :

\[ \begin{array}{ccc} \boldsymbol{\Phi}(t,\mathbf{x}_{0}) & = & \{\mathbf{x}(t)\,|\,\exists\mathbf{u}\in\mathbb{U},\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},\mathbf{u}),\mathbf{x}\left(0\right)=\mathbf{x}_{0}\}.\end{array} \]

Cette formulation nous dit que si l’état \(\mathbf{x}\) appartient à l’ensemble \(\boldsymbol{\Phi}(t,\mathbf{x}_{0})\), alors si le navigateur manœuvre correctement (plus précisément, s’il choisit \(\mathbf{u}\) comme réglage pour son système) il pourra atteindre l’état \(\mathbf{x}\) à l’instant \(t\) à partir de l’état initial \(\mathbf{x}_{0}\). Le navigateur qui est parti de \(\mathbf{x}_{0}\) a la connaissance de sa dynamique à travers cette équation du flot dans le cas d’un robot, ou bien grâce à un mécanisme neuronal dans le cas d’un navigateur humain.

Zone visible

Le navigateur est capable de percevoir son environnement. On définit la zone visible \(\mathbb{V}\left(\mathbf{x}\right)\) comme l’ensemble des points de l’espace que le navigateur peut voir sachant qu’il est dans l’état \(\mathbf{x}\), dans notre exemple la position. Par exemple, si le navigateur peut voir jusqu’à une distance de 1000 m, on a l’expression mathématique définissant cette zone

\[ \begin{array}{l} \mathbb{V}(\mathbf{x})=\left\{ \left(z_{1},z_{2}\right)|\sqrt{\left(z_{1}-x_{1}\right)^{2}+\left(z_{2}-x_{2}\right)^{2}}\leq1000\right\} \end{array} \]

qui correspond à l’équation d’un disque de centre \(\mathbf{x}=(x_{1},x_{2})\) et de rayon 1000 m. La figure 6 ci-après montre la zone \(\mathbb{V}(\mathbf{x}(0))\) vue par le navigateur à l’instant \(t=0\) et la zone \(\mathbb{V}(\mathbf{x}(t))\) vue à l’instant \(t\).

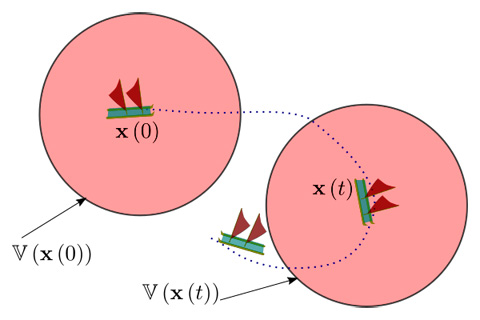
Fig. 6. Le navigateur perçoit à chaque instant une zone de l’océan centrée sur son bateau.

Mais, du fait de l’incertitude sur \(\mathbf{u}\), le navigateur connaît seulement un ensemble \(\mathcal{X}(t)\) de valeurs possibles pour sa position à l’instant \(t\). Il sait par exemple qu’il se trouve dans le carré bleu de la figure 7.

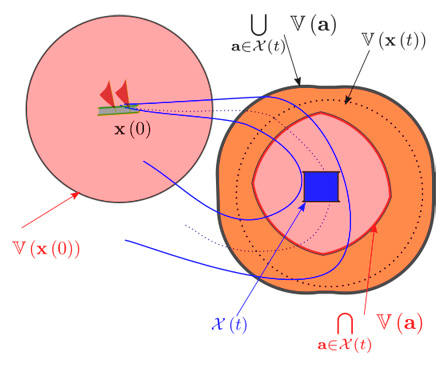
Fig. 7. Le bateau est dans le carré bleu à l’instant t ; il perçoit une zone \(\mathbb{V}(\mathbf{x}(t))\). Cette zone est incertaine, puisque le navigateur lui-même a une position mal connue ; la zone en orange, appelée pénombre, est l’ensemble des points que le navigateur peut voir, mais peut aussi ne pas voir.

La zone \(\mathbb{V}(\mathbf{x}(t))\) qu’il perçoit quand il est dans l’état \(\mathbf{x}(t)\) donc est elle aussi incertaine. Mathématiquement, on peut écrire

\[ \underset{=\mathbb{V}^{-}(t)}{\underbrace{\bigcap\limits _{\mathbf{a}\in\mathcal{X}\left(t\right)}\mathbb{V}\left(\mathbf{a}\right)}}\,\,\subset\,\,\,\mathbb{V}(\mathbf{x}(t))\,\,\,\subset\,\,\underset{=\mathbb{V}^{+}(t)}{\underbrace{\bigcup\limits _{\mathbf{a}\in\mathcal{X}\left(t\right)}\,\,~\mathbb{V}\left(\mathbf{a}\right)}}. \]

L’ensemble \(\mathbb{V}(\mathbf{x}(t))\) est donc un ensemble incertain. On sait seulement qu’il contient une zone \(\mathbb{V}^{-}(t)\) vue à coup sûr (à gauche dans la formule) et qu’il est contenu dans \(\mathbb{V}^{+}(t)\) la zone possiblement vue (à droite dans la formule). Ce couple de deux ensembles est un intervalle d’ensembles, appelé ensemble épais. On pourra noter

\[ \mathbb{V}(\mathbf{x}(t))\in\left[\mathbb{V}^{-}(t)\,,\,\mathbb{V}^{+}(t)\right]. \]

L’ensemble des points qui sont dans \(\mathbb{V}^{+}(t)\) et qui ne sont pas dans \(\mathbb{V}^{-}(t)\) est appelé la pénombre et est représenté en orange sur la figure 7. Lorsque l’on veut manipuler de tels ensembles incertains, sur ordinateur, on utilise principalement le calcul par intervalles.

Zone explorée

Nous définissons la zone explorée comme l’union \(\mathbb{Z}\) à chaque instant de ce qui a été vu par le navigateur. Cette zone peut être définie comme suit :

\[ \left\{ \begin{array}{c} \dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right),~\mathbf{u}\left(t\right)\in\mathbb{U}\left(t\right)\\ \mathbb{Z}=\bigcup_{t\geq0}~\mathbb{V}\left(\mathbf{x}\left(t\right)\right)\\ \mathbf{x}\left(0\right)=\mathbf{x}_{0} \end{array}\right. \]

Nous pouvons à nouveau encadrer cette zone entre deux zones \(\mathbb{Z}^{-},\mathbb{Z}^{+}\) comme suit :

\[ \underset{=\mathbb{Z}^{-}}{\underbrace{\bigcap\limits _{\mathbf{x}\in\mathcal{X}}\,\,\,~\bigcup\limits _{t\geq0}\mathbb{V}\left(\mathbf{x}\left(t\right)\right)}}\,\,\,\,\subset\,\,\,\mathbb{Z}\,\,\,\subset\,\,\,\,\underset{=\mathbb{Z}^{+}}{\underbrace{\bigcup\limits _{\mathbf{x}\in\mathcal{X}}\,\,~\bigcup\limits _{t\geq0}\mathbb{V}\left(\mathbf{x}\left(t\right)\right)}}\text{} \]

où \(\mathcal{X}\) est l’ensemble des trajectoires pour le bateau compatibles avec la condition initiale \(\mathbf{x}(0)\) et les incertitudes de navigation \(\mathbb{U}\left(t\right)\). \(\mathbb{Z}^{-}\) est l’ensemble des points vus à coup sûr, \(\mathbb{Z}^{+}\) est l’ensemble des points qui ont été possiblement vus (voir figure 8 ci-dessous). Cette zone explorée \(\mathbb{Z}\) peut être associée à une mission déjà faite : on cherche à savoir ce que l’on a exploré une fois la mission effectuée. Mais \(\mathbb{Z}\) peut également correspondre à une mission future pour laquelle on appliquera une stratégie de navigation fixée : on n’est toujours pas parti et on aimerait savoir ce que l’on va explorer.

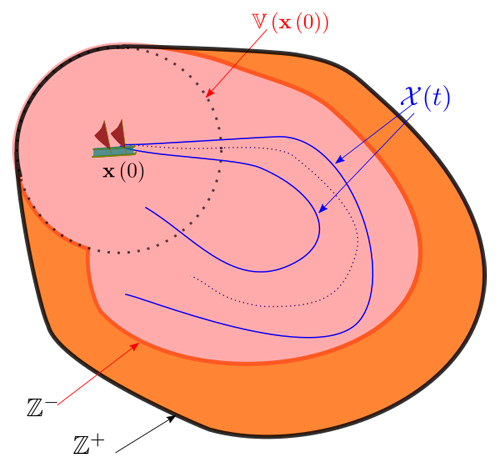
Fig. 8. Représentation de la zone explorée, qui est incertaine, du fait des incertitudes sur la trajectoire.

Un océan avec une seule île

Considérons le cas où le navigateur vit sur une île \(\mathbb{A}\) qu’il connaît bien et qui est entourée d’océan. Ici, l’île \(\mathbb{A}\) est vue comme un ensemble connexe du monde. Par connexe, on veut dire que l’on peut aller de tout point de \(\mathbb{A}\) à tout autre point de \(\mathbb{A}\) sans mettre un pied dans l’océan. Supposons que le navigateur dispose d’une carte métrique de cette île. Quelle zone de l’océan peut-il explorer tout en étant capable de revenir ? C’est le problème explore and return initié en robotique par Newman et Léonard.

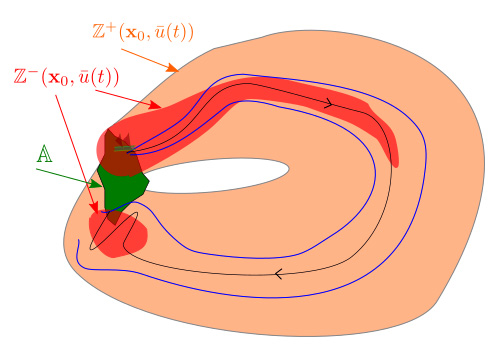
Fig. 9. Si le navigateur applique la stratégie \(\bar{u}(t)\), il restera dans le tube de trajectoires (en bleu), il verra tous les points dans \(\mathbb{Z}^{-}(\mathbf{x}_{0},\bar{u}(t))\) et ne verra aucun point à l’extérieur de \(\mathbb{Z}^{+}(\mathbf{x}_{0},\bar{u}(t))\).

Supposons que le navigateur choisisse comme stratégie d’exploration : aller à l’est pendant une heure, aller au sud pendant 30 minutes, aller dans la direction supposée de l’île et osciller autour de l’île pour la retrouver (voir figure 9 ci-dessus). Cela revient à choisir une commande \(\bar{u}(t)\) qui avec l’incertitude nous donne l’ensemble \(\mathbb{U}(t)\). L’ensemble certainement exploré est donné par \(\mathbb{Z}^{-}(\mathbf{x}_{0},\bar{u}(t))\) en rouge sur la figure 9. Et celui qui a été possiblement exploré est \(\mathbb{Z}^{+}(\mathbf{x}_{0},\bar{u}(t))\) (en orange). On remarque que l’ensemble \(\mathbb{Z}^{-}(\mathbf{x}_{0},\bar{u}(t))\) disparaît puis réapparaît. La disparition se comprend bien du fait de l’augmentation de l’incertitude sur la position du bateau. La réapparition est plus surprenante. Elle est due à la spécificité de la trajectoire en fin de mission où le navigateur planifie une recherche de l’île. Cette recherche finale de l’île lui a permis d’explorer plus loin tout en étant certain de revoir son île. On comprend bien que, pour une stratégie d’exploration \(\bar{u}(t)\) fixée, si on ne va pas loin, on pourra aisément garantir le retour, et que si on va trop loin, on ne pourra plus rien garantir. L’idée est bien évidemment d’aller le plus loin possible tout en étant certain de pouvoir rentrer sur l’île.

On définit le monde \(\mathbb{W}(\mathbb{A})\) associé à l’île \(\mathbb{A}\) comme un ensemble épais encadré par les deux ensembles suivants :

• Le monde certain \(\mathbb{W}^{-}(\mathbb{A})=\bigcup_{\mathbf{x}_{0}\in\mathbb{A}}\bigcup_{\bar{u}}\mathbb{Z}^{-}(\mathbf{x}_{0},\bar{u}(t))\), qui est l’ensemble des points que le navigateur peut aller visiter sans se perdre.
• Le monde possible \(\mathbb{W}^{+}(\mathbb{A})=\bigcup_{\mathbf{x}_{0}\in\mathbb{A}}\bigcup_{\bar{u}}\mathbb{Z}^{+}(\mathbf{x}_{0},\bar{u}(t))\), qui est l’ensemble des points que le navigateur peut possiblement voir sans se perdre, mais il lui faut de la chance pour les trouver. Les points qui ne sont pas dans \(\mathbb{W}^{+}(\mathbb{A})\) pourront être également visités, mais le navigateur ne pourra plus garantir son retour, ce que l’on s’interdit.

La figure 10 ci-dessous illustre ce concept de monde certain et monde possible associé à l’île \(\mathbb{A}\).

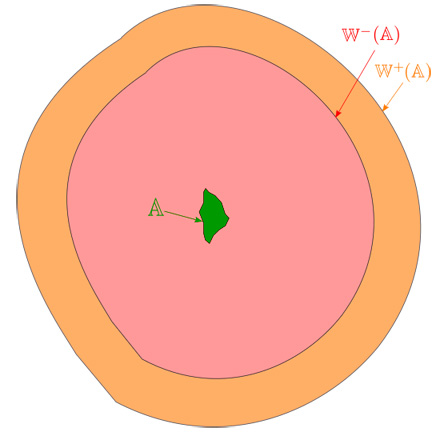
Fig. 10. En partant de son île \(\mathbb{A}\), si le navigateur voit un seul point à l’extérieur de \(\mathbb{W}^{+}(\mathbb{A})\), c’est qu’il ne pourra peut-être plus revenir sur son île.

Un océan avec deux îles

Supposons que nous ayons deux îles \(\mathbb{A}\) et \(\mathbb{B}\) où le monde possible \(\mathbb{W}^{+}(\mathbb{A})\) pour \(\mathbb{A}\) intersecte \(\mathbb{B}\), c’est-à-dire que \(\mathbb{W}^{+}(\mathbb{A})\cap\mathbb{B}\neq\emptyset\), comme sur la figure 11 (voir ci-dessous). Supposons que, en explorant les alentours de son île, le navigateur de l’île \(\mathbb{A}\) perçoive l’île \(\mathbb{B}\). Comme \(\mathbb{B}\) est dans la zone de pénombre du monde pour \(\mathbb{A}\), le navigateur sait que s’il rentre sur son île, il ne pourra peut-être jamais revoir l’île \(\mathbb{B}\). Malgré ce risque, imaginons que le navigateur prenne le risque d’aller sur \(\mathbb{B}\) sachant que, suite à cette décision, il ne pourra peut-être plus revenir sur son île \(\mathbb{A}\). Il prend connaissance de l’île \(\mathbb{B}\) qui, dans notre scénario, est plus grande. Par conséquent, il est probable que \(\mathbb{W}^{-}(\mathbb{B})\cap\mathbb{A}\neq\emptyset\) et donc à partir de \(\mathbb{B}\), il peut revenir sur \(\mathbb{A}\) quand il le veut. Mais comme l’île \(\mathbb{B}\) est plus grande, il saura également aller de \(\mathbb{A}\) à \(\mathbb{B}\).

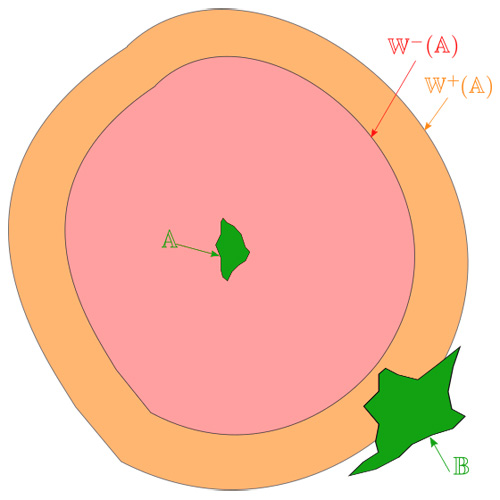
Fig. 11. Le navigateur vivant dans l’île \(\mathbb{A}\) découvre une île \(\mathbb{B}\).

Cela se traduit par la propriété suivante :

\[ \begin{array}{ccc} \mathbb{W}^{-}(\mathbb{A})\cup\mathbb{W}^{-}(\mathbb{B}) & \,\,\subset\,\, & \mathbb{W}^{-}(\mathbb{A}\cup\mathbb{B})\\ \mathbb{W}^{+}(\mathbb{A})\cup\mathbb{W}^{+}(\mathbb{B}) & \,\,\subset\,\, & \mathbb{W}^{+}(\mathbb{A}\cup\mathbb{B}) \end{array} \]

qui nous indique que le monde associé à un groupement d’îles est plus vaste que l’union des mondes associés à chacune des îles prises individuellement.

Ce principe se généralise à plus de deux îles. Ainsi, on étend de proche en proche le monde exploré jusqu’à ce que l’extension ne soit plus possible. Suivant la répartition des îles, il se peut que le monde explorable corresponde à l’univers tout entier.

Collaboration

Une autre façon pour le navigateur d’étendre encore plus son monde connu est de travailler de façon collaborative. Pour comprendre l’intérêt de cette collaboration, on peut imaginer deux navigateurs \(N_{1}\) et \(N_{2}\). Le navigateur \(N_{1}\) effectue un parcours avec retour. Le navigateur \(N_{2}\) suit \(N_{1}\), mais en s’autorisant une exploration autour de \(N_{1}\). Ils peuvent ainsi explorer plus loin s’ils sont deux. Mais, mieux que cela, imaginons un grand nombre de navigateurs partis explorer tellement loin de leur île que, individuellement, ils sont incapables de la retrouver. Ils peuvent à leur retour mailler collectivement la zone, à la manière d’un filet de pêche, de façon à ce que leur île ne puisse leur échapper. On retrouve à nouveau l’idée que la zone pouvant être explorée par un groupe de navigateurs est plus étendue que l’union des zones pouvant être explorées par chaque navigateur individuellement.

Conclusion

Dans cet article, deux approches pour la navigation ont été étudiées, avec comme fil rouge, la navigation polynésienne qui illustre parfaitement la difficulté de se déplacer dans un environnement non structuré sans se perdre. La première approche, dite topologique, cherche à suivre une succession de chemins élémentaires comme par exemple, suivre une rivière, longer un front isotherme sous-marin, suivre un parallèle, caboter. Cette technique permet de se déplacer dans un monde peu structuré comme les océans, les déserts, les fonds marins, les grottes, tout en étant capable de revenir à sa position initiale. Dans la navigation topologique, la notion de distance n’intervient pas. Seules les successions de chemins sont à mémoriser sous la forme d’un algorithme. Cette approche ancestrale de la navigation est également utilisée par les animaux marins, les pigeons et autres animaux migrateurs.

La deuxième approche pour la navigation est métrique. Elle repose sur la notion de carte métrique, comme celles que nous utilisons tous les jours pour nous déplacer avec notre propre véhicule. Elle permet d’explorer un monde totalement inconnu tout en étant capable de revenir et ceci en complétant notre carte du monde. Pour cela, la navigation métrique s’appuie sur la dynamique du véhicule, à travers une représentation par des équations différentielles. Les incertitudes sur les positions et les zones vues nous amènent à définir la notion d’ensembles épais sur lesquelles nous devons nous reposer pour garantir un retour à l’île initiale.

Notons que contrairement à la navigation moderne, dans la navigation polynésienne, on ne cherche pas à modifier son environnement en rajoutant des amers artificiels comme des phares ou des satellites GNSS (GPS ou Galiléo) ou encore comme le Petit Poucet qui déposait ses cailloux de repérage. Ce qui nous motive dans ce retour aux méthodes de navigation ancestrale, c’est l’exploration sous-marine par des robots. Le monde sous-marin est en effet un environnement gigantesque, non structuré, sans utilisation du GPS possible, sans la possibilité d’y déposer des amers. Les robots peuvent difficilement remonter à la surface pour refaire un point GPS du fait des risques de collisions avec les bateaux. Pourtant il est indispensable de nos jours d’être capable d’explorer le monde sous-marin, que cela soit pour retrouver des épaves, détecter des mines, surveiller les intrus pouvant entrer dans nos eaux (des sous-marins ennemis par exemple), rechercher des matières premières, vérifier l’état des stations offshore, signaler des pollutions possibles dans les eaux karstiques (rivières et lacs souterrains),etc. Cette navigation doit être fiable et autonome du fait de la difficulté de téléopération des robots sous-marins. En effet, contrairement à l’air ou l’espace, les ondes hertziennes sont fortement absorbées par l’eau, ce qui empêche une communication riche entre les humains et les robots sous-marins. Cette communication se limite à quelques rares ordres de haut niveau qui peuvent être transmis par le son. Ces robots doivent donc posséder leur propre ‘intelligence’, leur propre capacité de décision et un moyen de communication leur permettant de s’organiser et agir de façon cohérente et concertée.

Les méthodes de navigation polynésiennes peuvent être utiles dans d’autres types de missions dans des environnements labyrinthiques. C’est le cas pour l’exploration de villes après un séisme, la recherche de spéléologues égarés dans des grottes complexes, la cartographie des fonds des fleuves, la localisation sous la neige de victimes par des robots creuseurs, l’exploration de planètes lointaines, etc.