Les mathématiques du cœur

Notre cœur bat 100 000 fois par jour, soit près de 3 milliards de fois sans faillir au cours d’une vie humaine. Cette fiabilité est impressionnante ! Peut-on imaginer un produit manufacturé fonctionner aussi longtemps ? Une propriété fondamentale des systèmes vivants est leur capacité à se réparer en remplaçant leurs cellules mortes. Le cœur est quotidiennement soumis à du stress (activité physique, mauvaise alimentation…) et doit être capable de se réparer. Cependant, cette robustesse est limitée : les maladies cardiovasculaires tuent chaque année plus de personnes dans le monde que n’importe quelle autre cause. Selon l’OMS, les cardiopathies (maladies touchant le cœur) ont été responsables de 13% des décès en 2015.

Lors d’un infarctus, une partie du muscle cardiaque est privée de sang, causant la mort des cardiomyocytes, les cellules musculaires du cœur. Après l’infarctus, le tissu musculaire cicatrise, en remplaçant les cellules musculaires mortes par du tissu fibreux. Le cœur perd ainsi de sa capacité à pomper le sang. Les thérapies régénératives utilisent des cellules souches, l’ingénierie tissulaire ou des médicaments pour remplacer ou régénérer les organes afin de restaurer leurs fonctions, plutôt que de pallier leurs déficiences. Leur développement est un enjeu mondial pour l’amélioration de la qualité de vie et de la longévité après un infarctus.

L’incapacité du cœur à se régénérer peut paraître surprenante quand on considère que d’autres organes et tissus comme le foie et la peau peuvent guérir rapidement après une blessure. Cette observation a mené plusieurs groupes de recherche à évaluer la capacité du cœur adulte à produire de nouveaux cardiomyocytes. Jusque dans les années quatre-vingt-dix, il était communément admis que cette capacité diminuait rapidement après la naissance et devenait négligeable à l’âge adulte. L’augmentation du volume du cœur durant la croissance se fait principalement par hypertrophie, c’est-à-dire l’augmentation du volume des cellules existantes. Si aucun cardiomyocyte n’est généré chez l’adulte, comment expliquer la fiabilité du cœur ? Est-ce qu’il y aurait en fait plus de régénération qu’on ne le pense, mais que le cœur n’arrive pas à enclencher le bon « programme » de réparation dans les cardiopathies ? Une hypothèse est que le cœur n’a pas assez de cellules souches, ces cellules primitives qui peuvent donner naissance à toutes les cellules matures. La thérapie cellulaire est un type de thérapie régénérative basée sur la greffe ou l’injection de cellules humaines, comme les cellules souches mésenchymateuses ou hématopoïétiques. Plusieurs essais cliniques en cours testent l’efficacité de traitements par cellules souches à régénérer le tissu cardiaque et à en restaurer les capacités. Quel est donc le potentiel réel du cœur à se régénérer ?

Des retombées radioactives des essais nucléaires pour le moins inattendues

Durant la guerre froide, la course aux armements entre l’URSS et les États-Unis a conduit ces pays à effectuer des centaines d’essais nucléaires hors-sol. Entre 1955, date de la première détonation par les soviétiques, et 1963, date de la signature d’un traité interdisant les essais nucléaires hors-sol, plus de 500 détonations ont généré assez de carbone 14 (isotope radioactif du carbone, noté ¹⁴C) pour presque en doubler la concentration atmosphérique. Depuis 1963, la concentration de ¹⁴C diminue, principalement à cause de l’absorption dans les océans.

Cette évolution, avec le pic de 1963 suivi d’une décroissance, est la même que dans le contenu en ¹⁴C de l’ADN. En effet, les plantes et les animaux qui vivent des plantes absorbent le ¹⁴C atmosphérique, qui se retrouve dans notre alimentation et est utilisé lors de la synthèse de l’ADN. Il est ainsi possible de détecter de nouvelles cellules après la naissance d’une personne en rapportant le niveau de ¹⁴C mesuré contre la courbe atmosphérique (Figure 1). L’âge d’une cellule qui ne se divise plus est le temps écoulé depuis sa dernière division, et sa date de naissance est l’année où le contenu en ¹⁴C correspond au niveau atmosphérique. Cette méthode a été mise au point par Kirsty L. Spalding, Jonas Frisén et leurs collègues au Karolinska Institute à Stockholm dans les années 2000.

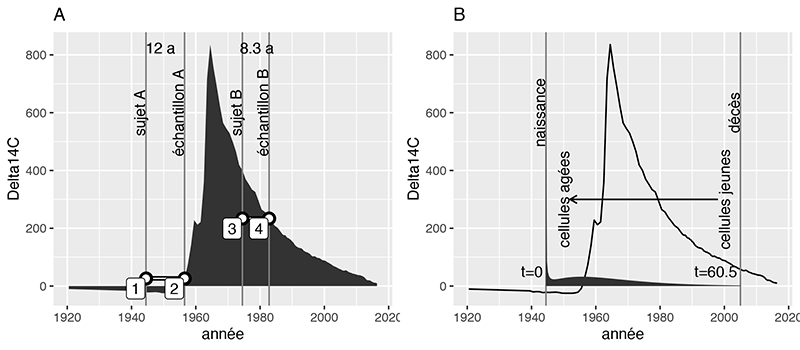
Figure 1 : (A) Datation au ¹⁴C. (1) Naissance du sujet A. (2) Le niveau de ¹⁴C des cellules correspond à une date plus récente de 12 ans. (3) Naissance du sujet B. (4) Le niveau de 14C des cellules correspond à une date plus récente de 8,3 ans. (B) Exemple d’évolution de taux de nouvelles cellules entre la naissance et le décès du sujet A. Les cellules acquièrent le niveau de ¹⁴C correspondant au niveau atmosphérique.

Le rôle des modèles mathématiques

Pour déterminer si le cœur se renouvelle, le contenu en ¹⁴C dans l’ADN de cardiomyocytes humains a été mesuré chez des adultes d’âges différents. Ces données montrent que le niveau de ¹⁴C correspond à des dates plus récentes que la naissance des sujets, suggérant que les cellules ont été générées après la naissance. Pour évaluer combien de cellules ont été générées et quand, il faut recourir à la modélisation mathématique.

Un modèle est une simplification de la réalité qui permet de tester des hypothèses et le cas échéant, de quantifier l’importance d’un phénomène. Le modèle peut être expérimental comme dans les laboratoire de biologie, ou théorique, où les hypothèses sont testées par des équations ou des simulations informatiques. Une caractéristique souhaitée d’un modèle est de permettre d’établir des liens de causalité entre différentes observations.

Ici, nous nous intéressons à un modèle théorique mathématique : nous voulons tester l’effet de l’arrivée de nouvelles cellules sur les niveaux de ¹⁴C à l’aide d’équations de naissance et de mort de cellules. Pour cela, nous devons concevoir un modèle qui décrit comment les cardiomyocytes meurent et sont remplacés tout au long de la vie humaine. Le modèle se base sur trois hypothèses :

1. Le nombre de cardiomyocytes ne varie pas substantiellement durant la vie.
2. Les cardiomyocytes peuvent mourir.
3. Les cardiomyocytes morts peuvent être remplacés par de nouveaux cardiomyocytes.

La réalité est plus complexe. En effet, les cardiomyocytes peuvent synthétiser de l’ADN sans se diviser. Il faudrait aussi prendre en compte cet effet, mais nous l’ignorerons ici.

Le ¹⁴C est mesuré dans un échantillon de plusieurs millions de cellules. On s’attend donc à ce que l’échantillon contienne des cellules de tous âges \(a\) compris entre 0 et l’âge \(t\) d’un sujet (Figure 1B). Soit \(n(t,a)\) le nombre de cellules d’âge \(a\) (en années) chez un sujet âgé de \(t\) ans, \(m(t,a)\) la fraction de cellules d’âge \(a\) qui meurent au temps \(t\), et \(g(t)\) le nombre de nouvelles cellules nées au temps \(t\). Alors

\begin{align*} n(t,a) & = n(t-1,a-1) (1 – m(t-1,a-1)), \text{ si } a>0, t>0, \\ n(t,0) & = g(t), \\ n(0,0) & = N_0, \\ n(0,a) & = 0, \text{ si } a>0. \end{align*}

La première équation décrit le fait que les cardiomyocytes gagnent un an d’âge chaque année, et peuvent mourir. La deuxième équation décrit le nombre de cellules générées dans l’année. Les troisième et quatrième équations spécifient que les \(N_0\) cellules à la naissance sont d’âge 0. Le nombre total de cellules \(N(t)\) est la somme des nombres de cellules dans chaque classe d’âge \(a\)

\begin{align*} N(t) = \sum_{a=0}^{t} n(t,a). \end{align*}

Si les cellules nées à l’année calendaire \(y\) intègrent le niveau de ¹⁴C atmosphérique correspondant \(K(y)\), le niveau de ¹⁴C dans la population de cellules collectées à la date \(y_c\) (correspondant à la date du décès) sera

\begin{align*} C = \frac{1}{N(t)} \sum_{a=0}^{t} n(t,a) K(y_c-a), \end{align*}

c’est à dire que le niveau de ¹⁴C dans la population est la moyenne pondérée par le nombre de cellules de chaque classe d’âge.

Il s’agit donc de trouver une courbe de mortalité \(m\) qui corresponde au mieux aux données humaines, pour déterminer combien de cellules sont remplacées chaque année. En testant différents scénarios, on trouve que la génération de nouvelles cellules se poursuit tout au long de la vie. Cependant, elle décroît rapidement durant l’enfance. Environ 80% des nouvelles cellules sont générées dans les 10 premières années de vie (Figure 2A). Près de 1% des cardiomyocytes sont remplacés chaque année chez les jeunes adultes, et ce pourcentage décroît à moins de 0,5% chez les personnes âgées (Figure 2B). Le meilleur scénario indique que le taux de mortalité \(m(t,a)\) diminue avec l’âge des cellules \(a\). En vieillissant, les cellules cardiaques sont remplacées de moins en moins fréquemment.

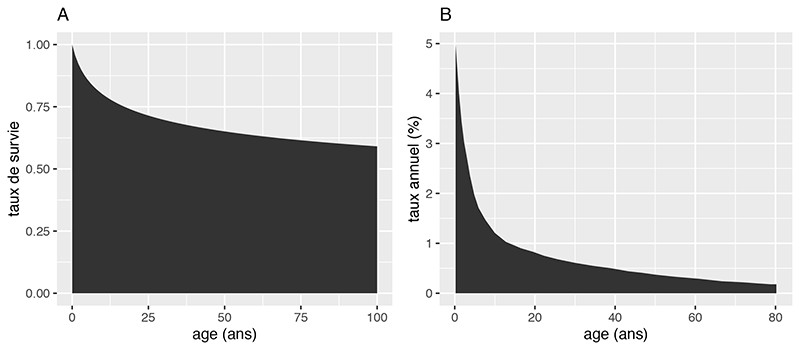
Figure 2 : (A) Fraction des cardiomyocytes présents depuis la naissance en fonction de l’âge de la personne. À 50 ans par exemple, environ 65% des cardiomyocytes n’ont jamais été remplacés. (B) Taux effectif annuel de renouvellement de cardiomyocytes en fonction de l’âge de la personne.

Entre spéculation et espoir

Ces résultats sont le produit d’une collaboration entre sciences expérimentales et mathématiques appliquées. Ils s’inscrivent dans un contexte où de nombreuses équipes de recherche tentent de mettre au point des stratégies de régénération du muscle cardiaque pour lutter contre les maladies cardiovasculaires. La présence de nouveaux cardiomyocytes dans le cœur adulte, même en petit nombre, donne l’espoir que les thérapies cellulaires puissent produire des cellules qui vont intégrer durablement le muscle cardiaque et en améliorer la fonction. Malheureusement, les thérapies cellulaires peinent à tenir leur promesses, et la confusion règne sur la validité de certains résultats fondamentaux qui les ont motivées. Il semblerait que leurs effets thérapeutiques ne soient pas dus à l’intégration de nouveaux cardiomyocytes.

Les taux de renouvellement que nous avons estimés chez les sujets sains sont largement insuffisants pour réparer le cœur après un incident cardiaque. Cependant, notre modèle de renouvellement cellulaire prédit que les cellules immatures (jeunes) ont une durée de vie moins longue que les cellules intégrées au tissu depuis longtemps. Comme la datation ¹⁴C ne mesure que ces dernières, nous avons peut-être sous-estimé la production de nouveaux cardiomyocytes, ce qui indiquerait que le potentiel régénératif est en fait limité par la difficulté à intégrer physiquement le tissu et à survivre, et non par le manque de cellules souches. Une stratégie thérapeutique pourrait donc être de faciliter la survie et l’intégration des nouvelles cellules, plutôt que d’en stimuler la production. En limitant la formation de tissu fibreux après un infarctus, il serait peut-être possible de produire un environnement favorable à l’intégration de cellules musculaires du cœur.

La modélisation mathématique peut apporter un éclairage sur les limites et le potentiel des thérapies. En caractérisant la dynamique du renouvellement des cardiomyocytes dans les cœurs sains et pathologiques, il sera peut-être possible de mieux cibler et d’accroître l’efficacité des thérapies régénératives.