Pluies et inondations en milieu urbain

Les inondations pluviales

Les journaux télévisés, les vidéos en ligne et les réseaux sociaux nous ont depuis de nombreuses années habitués aux images d’inondations catastrophiques, en particulier dans les zones habitées. Dans le sud de la France par exemple, les processus pluvieux peuvent être intenses et très localisés notamment pendant l’automne. Des masses d’air humide provenant de la Méditerranée, dont l’eau est encore chaude, provoquent ces pluies en se déplaçant vers les contreforts de la chaîne de montagnes des Cévennes. On parle donc d’événements « cévenols ». Les zones urbaines imperméabilisées sont alors fortement affectées par ces pluies. Les infrastructures telles que collecteurs et bassins de rétention saturent et le ruissellement sur les toits et dans les rues est susceptible de faire monter le niveau de l’eau de plus d’un mètre en moins d’une heure. Outre l’impact du changement climatique, la recrudescence des inondations urbaines des dernières années s’explique surtout par l’urbanisation croissante. Les grandes agglomérations concentrent en France la plus grande partie de l’accroissement de la population. Par rapport aux décennies précédentes, la population afflue désormais dans les communes périphériques des grandes villes au lieu de peupler leur centre. L’urbanisation s’accompagne d’une imperméabilisation conséquente des surfaces (habitations, zones d’activités, parkings, routes, etc.). Des pluies intenses qui, avant l’urbanisation, auraient pu s’infiltrer dans les sols ou être « amorties » par le milieu naturel sont maintenant transférées en surface, de façon très rapide sur les versants (surfaces inclinées) et dans les réseaux de collecte des eaux pluviales, qui peuvent déborder localement. Comme on construit principalement dans les zones plates (les fonds de vallées, les lits majeurs de cours d’eau), où l’eau s’évacue plus difficilement, le ruissellement qui résulte des événements pluvieux affecte désormais des zones qui, il y a quelques décennies, n’étaient pas habitées. L’urbanisation introduit donc une « double peine » : non seulement elle accroît les volumes d’eau qui ruissellent, mais de plus elle conduit à ce que les événements hydrologiques intenses affectent davantage de personnes et de biens.

La prise de conscience des responsables politiques s’est notamment traduite par l’adoption, à l’échelon européen, de la Directive Cadre Inondation. Une des nombreuses dispositions de cette Directive Cadre fait obligation aux collectivités de remettre à jour périodiquement les cartes de risque d’inondation sur leur territoire.

Les acteurs impliqués dans le risque d’inondation sont nombreux : collectivités locales (services d’urbanisme, d’aménagement du territoire), services de secours et de protection civile, mais également assureurs, etc. Tous ces acteurs sont demandeurs de solutions qui leur permettraient de gérer plus efficacement la crise que représente une inondation. Avant et après la crise, il est nécessaire de mettre en place des mesures de prévention et de mitigation des risques (aménagement de zones de rétention, définition des périmètres inondables). Pendant la crise, il faut pouvoir gérer les communications, l’organisation des secours, la protection des zones sensibles (hôpitaux, écoles, centres de distribution de communications et d’énergie). Dans l’idéal, les décideurs souhaiteraient pouvoir prévoir en temps réel ou quasi réel comment l’événement pluvieux intense va se comporter (comment va-t-il se déplacer, comment son intensité va-t-elle varier ?), pour pouvoir ensuite déterminer comment l’eau va ruisseler sur les différentes parties de l’agglomération.

La modélisation stochastique des champs de pluie

Les bureaux d’études et les scientifiques disposent de modèles leur permettant de simuler l’hydraulique des inondations à partir de champs de pluie, c’est-à-dire à partir d’une quantité de pluie souvent exprimée en millimètres par heure sur une zone d’étude pour une période de temps fixée. Plus précisément, ils calculent en tout point de la zone étudiée et à chaque instant des hauteurs et des vitesses d’eau. Ce résultat dépend directement du champ de pluie fourni. Ce dernier peut être lui-même issu d’un modèle de prévision météorologique ou correspondre à des mesures réelles. Une autre possibilité est de s’appuyer sur ces données et de considérer des approches stochastiques, basées sur la théorie des probabilités, qui simulent des champs de pluie en incluant un aspect aléatoire. Cela permet la création d’un nombre illimité de scénarios dont on peut contrôler les particularités.

Dans ce cadre, un modèle stochastique cherche à représenter un champ de pluie. En chaque point et en chaque temps, l’intensité de pluie doit être positive ou nulle, ce qui n’est pas vérifié par tous les modèles. Pour produire des simulations de champs de pluie réalistes, prendre en compte à la fois les absences de pluie, les pluies moyennes et les pluies intenses est capital et fait l’objet de recherches en cours. Une façon de faire est de considérer plusieurs types de pluie et d’avoir un modèle par type. Restera ensuite à combiner les simulations issues de chaque type de pluie dans un modèle global. Pour l’étude du risque inondation, il est important d’intégrer les pluies intenses car elles peuvent avoir des dégâts considérables. Par exemple, les événements « cévenols » sont à la fois rares et extrêmes. Ayant pour fondement la théorie probabiliste des valeurs extrêmes, certains modèles spécifiques sont utilisés pour estimer des quantités telles que la fréquence d’un événement extrême ou son apparition pendant une période donnée. Devant la rareté des données, il s’agit alors d’extrapoler pour estimer par exemple une quantité de pluie centennale en disposant de seulement 20 ans d’observations.

Puisque la pluie varie dans le temps et dans l’espace, le modèle doit intégrer cette dépendance spatio-temporelle. Cette modélisation est complexe, aussi nous illustrons ici seulement la dépendance spatiale. Si la pluie varie dans l’espace, elle tend cependant à prendre des valeurs semblables en des points géographiquement proches. Un processus aléatoire représente la pluie en tous les points de l’espace considéré en tenant compte de cette dépendance spatiale. Dans certains modèles, cette dépendance spatiale entre les intensités de pluie correspond à ce qu’on appelle la corrélation. Des points peuvent avoir tendance à varier de la même façon (corrélation positive), de façon contraire (corrélation négative) ou de façon indépendante (corrélation nulle). On fait généralement l’hypothèse que la corrélation entre deux points dépend de la distance entre ces deux points. C’est une idée qui paraît assez naturelle : plus les points sont éloignés, plus leur dépendance spatiale est faible. Ces coefficients de corrélation et d’autres paramètres du modèle doivent être estimés pour reproduire au mieux des phénomènes réels. En pratique, on dispose de mesures grâce aux stations d’observations (pluviomètres…) positionnées en quelques points. À l’aide de ces observations, des valeurs sont attribuées aux paramètres du processus par une méthode statistique. On parle alors d’estimation des paramètres du modèle. Il est ensuite possible de simuler autant d’événements pluvieux que l’on souhaite, qui sont proches de la réalité.

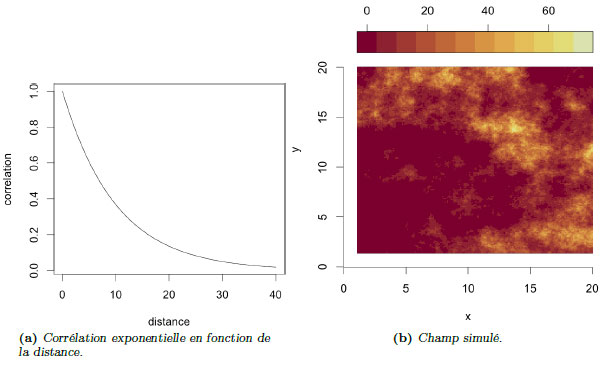
Figures 1a et 1b. La figure 1a illustre un exemple de corrélation exponentielle en fonction de la distance entre les points. On remarque que lorsque la distance augmente entre deux points, la corrélation décroît. La figure 1b représente la simulation par un processus aléatoire gaussien de l’intensité d’une pluie (en mm/h) sur un domaine carré de 20 km par 20 km, obtenue en utilisant la fonction de corrélation de la figure 1a.

La modélisation hydraulique urbaine

À l’étape suivante de la chaîne de gestion de crise, les champs de pluie alimentent des modèles hydrauliques pour simuler les inondations en milieu urbain. En pratique, mettre en œuvre ces modèles pour répondre aux besoins spécifiques de la crise « inondation urbaine » n’est pas si aisé. Les modèles hydrauliques peuvent simuler différents scénarios d’épisodes pluvieux, par exemple pour anticiper les risques d’inondation. Pour simuler la propagation d’une crue, qu’elle soit due au débordement d’un cours d’eau ou au ruissellement urbain, un logiciel calcule l’évolution des hauteurs et vitesses de l’eau dans le milieu urbain, pendant la durée de l’épisode pluvieux, soit plusieurs heures voire plusieurs jours. Pour faire ces calculs, il faut d’une part décrire la géométrie de la zone d’étude avec une grande précision, chaque rue, immeuble, rond-point, etc. Les obstacles tels que les trottoirs ou le mobilier urbain peuvent jouer un rôle déterminant et sont difficilement pris en compte. Il faut aussi connaître la topographie du domaine (l’altitude en chaque point). D’autre part, il faut évaluer la quantité de pluie apportée à la zone d’étude et sa répartition dans l’espace et dans le temps. C’est le rôle des modèles stochastiques décrits précédemment. Enfin, de l’eau peut arriver au bord de la zone, par une rivière par exemple, ou sortir de la zone en aval. Parfois, la hauteur d’eau au bord est déterminée par une station d’observation, mais il est fréquent qu’aucune mesure ne soit disponible.

Les logiciels de simulation et prévision de crue urbaine utilisent un modèle d’écoulement de l’eau où la hauteur n’est pas contrainte (surface libre). Il s’agit de résoudre des équations, issues de lois physiques, dont les inconnues sont la hauteur et la vitesse de l’eau en chaque point du domaine et à chaque instant. Il n’est pas possible de résoudre exactement ces équations, alors le logiciel utilise un modèle approché, qui remplace le domaine infini par un nombre fini de points. La précision des approximations augmente en général avec le nombre de points. Ceux-ci sont reliés entre eux pour former un ensemble de cellules, appelées mailles. La difficulté principale est la suivante : en milieu urbain, il est indispensable de faire les calculs en un grand nombre de points pour simuler fidèlement l’évolution des hauteurs d’eau. Une dizaine de mailles est nécessaire sur la largeur des rues, et il faut parfois des mailles de moins d’un mètre pour discrétiser correctement la géométrie. Cela signifie typiquement une dizaine à une centaine de mailles par mètre carré, soit un point tous les 10 centimètres dans les deux directions. Pour une agglomération carrée de 10 km de côté, on obtient ainsi un milliard à 10 milliards de mailles. De même, les calculs ne peuvent pas être faits à chaque instant, mais seulement à intervalles de temps réguliers. Une deuxième difficulté surgit : le pas de temps (durée entre deux instants de calcul) doit être proportionnel à la taille de maille pour garantir la qualité des résultats. Les puissances de calcul nécessaires sont inaccessibles à l’heure actuelle. Prenons l’exemple du quartier centre de la ville de Montpellier, illustré sur la figure 2 ci-dessous. Dans cette zone carrée de 600 m par 600 m, la simulation a été faite avec un maillage de 45 000 mailles. Le détail de la figure 2 montre que pour certaines ruelles de 2 m de large, seules deux mailles sont utilisées en travers de la rue. Les résultats de simulation de la figure 2 donnent une première indication. Néanmoins, le maillage est ici trop grossier, il faudrait environ 300 000 mailles pour obtenir des résultats précis.

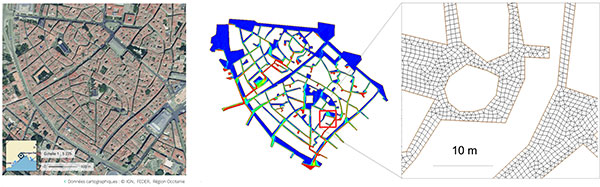
Figure 2. Exemple de hauteurs d’eau et de vitesses simulées sur le centre de la ville de Montpellier en utilisant une pluie stochastique. À gauche : vue aérienne de la zone d’étude (600 m × 600 m). Au centre : hauteurs d’eau simulées, les plus faibles sont en bleu, les plus grandes (5 cm) en rouge. À droite : vue de détail du maillage, montrant seulement deux mailles dans certaines ruelles.

Les bureaux d’études construisent habituellement des modèles d’inondation de 100 à 500 000 mailles. Une taille respectable, bien loin cependant de permettre le calcul d’une crue à l’échelle de l’agglomération. À l’heure actuelle, il n’est possible de simuler des inondations qu’à l’échelle du quartier.

Les modèles hydrauliques avec transfert d’échelle

Une piste de recherche prometteuse pour répondre à la problématique du temps de calcul et de la représentation précise de la géométrie du milieu urbain, consiste à effectuer un « transfert d’échelle ». Dans cette approche, aussi appelée « upscaling », on ne cherche pas à résoudre finement les équations qui décrivent les écoulements mais à les résoudre « en moyenne » sur de grandes étendues. L’upscaling des modèles d’inondation urbaine mobilise un intérêt croissant de la part de la communauté scientifique depuis une dizaine d’années. Pour les applications urbaines, une maille de calcul couvrira typiquement un pâté de maisons, pour une taille allant de la dizaine à la cinquantaine de mètres. La zone urbaine de la figure 2 ci-dessus pourrait alors être couverte par 100 à 300 mailles en fonction du degré de précision attendu. Le calcul d’upscaling est alors 1 000 à 10 000 fois plus rapide que celui du modèle « classique », ce qui permet d’envisager les prévisions en temps réel ou quasi réel évoquées plus tôt. En moyennant les équations des écoulements à surface libre sur une zone urbaine, on obtient des équations modifiées, où de nouveaux termes apparaissent du fait de la présence d’une phase solide (le bâti). La géométrie urbaine est décrite de manière statistique, par des paramètres qui décrivent les fractions de l’espace disponibles à l’écoulement, les orientations des axes majeurs de voirie, etc. Pour identifier ces nouveaux termes et ces paramètres, il faut ajouter des équations dites « de fermeture », qui précisent les relations entre les variables moyennes et les variables à échelle fine. C’est une difficulté de cette approche, sur laquelle travaillent de nombreuses équipes de recherche.

Le potentiel de l’upscaling est illustré par la simulation d’une onde de submersion résultant de la rupture d’une digue dans un lotissement de la banlieue de Sacramento aux États-Unis (voir figure 3 ci-dessous). La digue sépare le lotissement d’un canal de navigation. Dans ce canal, la surface de l’eau est située plus haut que le terrain construit dans le lotissement. Une rupture de digue exposerait les habitants à un risque d’inondation et à des dommages élevés.

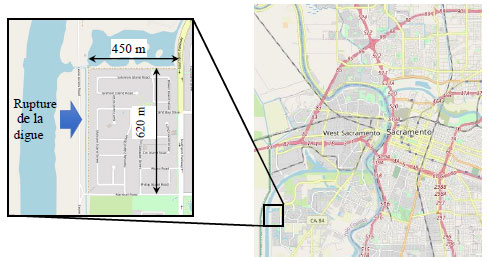
Figure 3. Simulation de rupture de digue dans un lotissement de la ville de Sacramento (Californie). Plan de situation.

Une rupture instantanée de la digue a été simulée en résolvant les équations des écoulements à surface libre de façon classique (figure 4, à gauche). Le maillage très fin, avec plus de 78 000 mailles de 1 mètre chacune environ, permet de simuler avec un bon niveau de détail les réflexions de l’onde de submersion sur les bâtiments et le contournement de ceux-ci par l’écoulement. En comparaison, le modèle avec upscaling, dit « DIP », publié en 2017 (résultats de simulation figure 5, droite) compte moins de 2 500 cellules et est 500 fois plus rapide que le modèle classique. Bien qu’il ne permette pas de restituer le même niveau de détail, la plage de variation des hauteurs d’eau et des vitesses moyennes, ainsi que les grandes directions de propagation d’onde, sont restituées avec une précision suffisante en pratique.

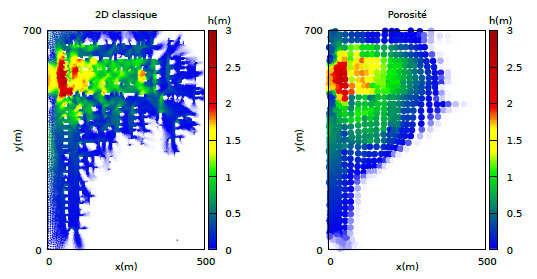
Figure 4. Simulation d’une rupture de digue sur un lotissement de la ville de Sacramento. À gauche : onde de rupture simulée avec le modèle fin classique. À droite : onde de rupture simulée à l’aide du modèle DIP avec upscaling.

Cette simulation montre tout l’intérêt du modèle avec upscaling (sa rapidité), mais illustre également ses limites en termes de précision : le modèle avec upscaling ne produit que des valeurs moyennes sur de grandes étendues. Or, pour les décideurs et les gestionnaires de crise, ces valeurs moyennes peuvent être insuffisantes. Pour gérer la crise d’inondation, il faut être en mesure de prévoir que telle rue va être inondée, empêchant l’acheminement des secours ; ou que telle zone à enjeu fort (une école, un hôpital, un transformateur électrique, etc.) est menacée. Il faut donc, à partir de la simulation grossière du modèle avec upscaling, pouvoir produire une cartographie fine des variables hydrauliques, à l’échelle du mètre. C’est ce que l’on appelle la « désagrégation » ou « downscaling », le processus inverse de l’upscaling. Le downscaling est beaucoup utilisé dans le domaine de la météorologie, mais son utilisation dans le domaine des inondations urbaines pose des problèmes spécifiques auxquels la communauté des scientifiques commence tout juste de s’intéresser.

Pour aller plus loin

On a vu qu’il est possible, à l’heure actuelle, de simuler avec précision les écoulements survenant lors d’une inondation. Cependant, les modèles sont encore limités par deux aspects principaux : les données nécessaires à leur application (géométrie du domaine, pluies et débits entrants…) et l’étendue sur laquelle ils peuvent concrètement être mis en place (celle d’un quartier seulement).

Dans l’objectif de prédire et alerter au mieux lors d’un événement pluvieux, ces questions sont abordées sous différents angles par de nombreuses équipes de recherche : simulateurs de pluies, estimation des paramètres par données satellites, mise en place de réseaux d’observations, développement de modèles à large échelle, etc.