L’analyse par ondelettes dans la vie de tous les jours

L’analyse du signal est une discipline scientifique qui essaie de comprendre les signaux grâce aux mathématiques.  Le mot « signal » est à prendre au sens large. Cela veut dire qu’un signal peut être une fonction dépendant d’une variable, comme un ECG qui est une intensité électrique dépendant du temps. Ou encore, un signal peut être une image qui est une fonction couleur dépendant de deux variables indiquant la position du pixel. Les ondelettes constituent un outil célèbre en analyse du signal. Faire une analyse par ondelettes d’un signal veut dire essayer de comprendre toutes les informations présentes dans le signal en utilisant cet outil.

Comment fonctionne une « analyse par ondelettes » ?

Une ondelette est une fonction oscillante (ce qui explique le mot « onde ») de moyenne nulle, appelée ψ. Son support, intervalle sur lequel l’ondelette est non nulle, est fini (ce qui explique le mot « ondelette », qui veut dire petite onde).

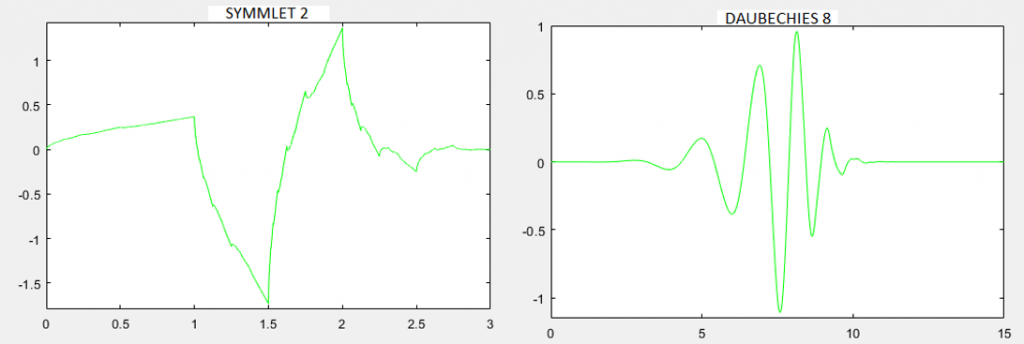
Exemples d’ondelette mère ψ(t)

L’ondelette mère ψ génère une famille d’ondelettes `ψ_{u,s}(t)` où `u` est le paramètre du temps et `s` le paramètre d’échelle. L’ondelette `ψ_{u,s}` est simplement l’ondelette mère ψ translatée de `u` et, soit dilatée par `s` si `s` > 1, soit contractée par `s` si `s` < 1, soit conservée si `s` = 1. Par conséquent, quand l’échelle `s` augmente, le support de l’ondelette augmente.

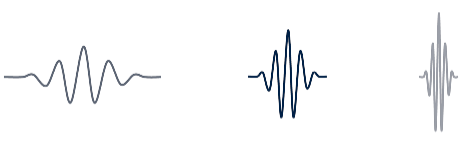
Ondelette-mère au centre, dilatée à gauche et contractée à droite

La représentation de l’analyse par ondelettes d’un signal se fait sous forme d’image avec le temps `u` en axe horizontal et l’échelle `s` en axe vertical. Chaque pixel de l’image représente un coefficient d’ondelette. Le coefficient d’ondelette au temps `u` et à l’échelle `s` est un nombre réel correspondant à la ressemblance entre le signal étudié (noté `f`) et l’ondelette `ψ_{u,s}`. Concrètement, cette ressemblance se calcule au moyen d’un produit scalaire `\(int_{-\infty}^{\infty}f(t)\ψ^**‍_{u,s}(t)dt)`. Ci-dessous, on voit qu’un signal régulier, c’est-à-dire plus lisse, (cas 1, à droite) se traduira par des coefficients d’ondelettes faibles. À l’inverse, un signal irrégulier, c’est-à-dire plus chahuté, (cas 2, à gauche) possèdera des coefficients d’ondelettes d’autant plus importants que ses fluctuations correspondent à la forme de l’ondelette utilisée (Meyer et al., 1987).

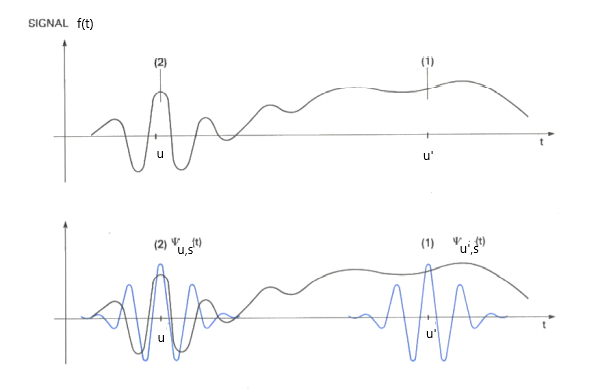
Interprétation géométrique des coefficients d’ondelettes (Meyer et al., 1987). À gauche, le signal ressemble à l’ondelette, dès lors le coefficient d’ondelettes correspondant est élevé. À droite, le signal ne ressemble pas à l’ondelette, dès lors le coefficient d’ondelettes correspondant est faible. © DR Meyer Y., Jaffard S. & Rioul O

La figure ci-dessous contient un signal et sa représentation en ondelettes. Plus un point est jaune, plus le coefficient en ondelettes correspondant est grand dans les positifs. Plus un point est bleu, plus le coefficient en ondelettes correspondant est grand dans les négatifs. Les autres coefficients sont tous proches de zéro. Par exemple, un point jaune au temps 850 et à l’échelle 300 correspond à un coefficient d’ondelette d’une grande valeur au temps 850 et à l’échelle 300. Cela spécifie qu’au temps 850 le signal est similaire à l’ondelette `ψ_{850,300}`

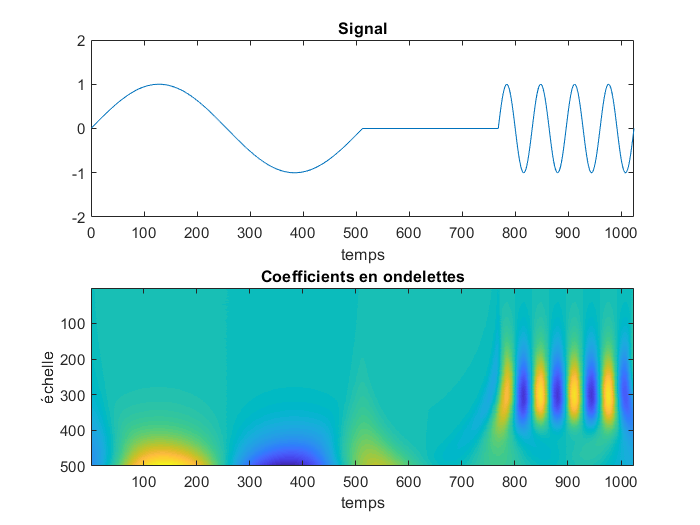
Signal (au dessus) et sa représentation en ondelette (en-dessous)

Pour une large gamme de signaux, un nombre important de coefficients d’ondelettes sont proches de 0, à condition de choisir une ondelette mère appropriée. On parle de représentation parcimonieuse du signal.

Du nettoyage de signaux expérimentaux ou de photos…

L’estimation de signaux dans du bruit est un grand exemple de l’efficacité des ondelettes. En fait, dans un bruit de fond de conversations anglaises, il est facile de suivre une discussion en français. De même, l’estimation d’un signal mêlé à du bruit peut s’optimiser en trouvant une représentation qui sépare le signal du bruit (Mallat, 1988). Par leur localisation en temps et en échelle, les ondelettes permettent une discrimination efficace du signal et du bruit. En effet, si l’ondelette mère est bien choisie, le signal a peu de coefficients importants alors que le bruit se répartit de façon minime sur tous les coefficients. La figure ci-dessous illustre ceci en montrant quelques coefficients d’ondelettes d’un signal avec et sans bruit.

Au-dessus, des coefficients d’ondelettes d’un signal f auquel on a ajouté du bruit. En-dessous, les  coefficients d’ondelettes du signal f sans l’ajout du bruit. On constate que le signal f est caractérisé par quelques grands coefficients d’ondelettes et que le bruit se répartit sur tous les coefficients d’ondelettes.

L’approche habituelle de Donoho (Donoho, 1995) pour se débarrasser du bruit se fait en trois étapes. La première consiste à calculer les coefficients d’ondelettes des données bruitées. La seconde enlève le bruit des coefficients d’ondelettes. Pour l’effectuer, différentes méthodes dites de seuillage existent, la plus radicale étant de mettre à zéro tous les petits coefficients d’ondelettes. Le fait d’être considéré comme un petit coefficient dépend des caractéristiques du bruit. La troisième calcule le signal débruité à partir des coefficients débruités par une opération inverse. Le succès de cette approche est principalement basé sur la représentation parcimonieuse en ondelettes d’une large gamme de fonctions. La figure ci-dessous illustre le débruitage d’un signal.

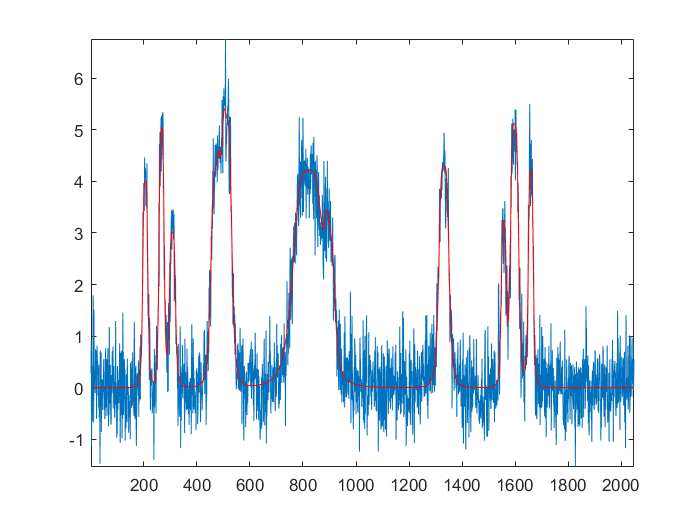
Débruitage par ondelettes d’un signal. En bleu le signal bruité et en rouge le signal débruité

De façon plus large, les images médicales sont souvent floues, avec peu de contraste, et exigent de pouvoir analyser les éléments d’étude à différentes échelles et de bien caractériser leur contour. Et, là aussi, les ondelettes s’imposent. On les retrouve donc en résonance magnétique, en mammographie et en biologie (Antoine, 2017). Et elles ne se limitent pas à la médecine puisqu’elles touchent de nombreuses applications de nos smartphones basées sur des photos (ajout de filtres, reconnaissance d’images, déverrouillage via empreinte digitale, etc.).

…à la compression de fichiers…

La compression de données fonctionne sur le même principe. La première étape consiste aussi à développer le signal à compresser en coefficients d’ondelettes. La deuxième étape sélectionne les quelques coefficients hautement significatifs, les autres contenant peu d’information étant mis à zéro. Cette étape, similaire au seuillage lors du débruitage de signaux, est malgré tout différente, notamment par son choix des coefficients seuillés. Enfin, il est alors facile de stocker avec peu d’espace mémoire cette représentation en ondelettes remplie d’éléments nuls. C’est la troisième étape. Pour visualiser l’image compressée, il faut faire la transformation inverse par ondelettes. Bien sûr, l’image compressée diffère légèrement de l’image de départ, mais les différences sont imperceptibles. Le format de compression JPEG2000 est basé sur les ondelettes.

Image originale à gauche et image compressée à droite

… en passant par les sciences environnementales

La transformation en ondelettes offre également la possibilité de fournir une information sur le lien entre différentes variables par observation de leurs événements communs. Dans ce cas, on utilise entre autres la cohérence en ondelettes qui renseigne quant à l’évolution simultanée de deux signaux. Elle met en évidence les mouvements périodiques d’amplitude quelconque qui affectent simultanément deux variables.

Cette application a été exploitée dans une multitude de cas dont le lien entre l’étendue de la glace dans la mer Baltique et l’échange de masse atmosphérique entre l’Arctique et le Nord Atlantique (Grinsted, 2004), le lien entre variables climatiques et mousson asiatique, ou la dépendance de la consommation électrique aux variables environnementales, pour n’en citer que trois.

En conclusion

Les ondelettes ont démontré leur puissance en analyse du signal. L’information développée ici est très brève et s’attache principalement à la transformation en ondelettes continue. En réalité, il existe différentes analyses par ondelettes comme par exemple la transformation en ondelettes discrètes, par paquets d’ondelettes ou par ondelettes orientées. Chacune est mieux adaptée dans un contexte précis. Et, comme l’analyse par Fourier a donné naissance à l’analyse par ondelettes, les ondelettes elles-mêmes à leur tour vont donner naissance à d’autres analyses. On parle de « ridgelets », « contourlets » ou « bandelets »… La science ne s’arrête jamais. Pour en savoir davantage sur la différence entre l’analyse par Fourier et celle par ondelettes ou sur la représentation d’une analyse par ondelettes, l’article « De la transformée de Fourier à la transformée par ondelettes : le succès de l’analyse temps-fréquence » est disponible.

L’auteur remercie le comité éditorial d’Interstices pour lui avoir proposé le sujet d’article et pour leur relecture attentive. Les figures ont été réalisées avec MatLab.