Indexer des milliards d’éléments avec les filtres de Bloom

On peut imaginer un cas classique d’utilisation où l’on cherche à savoir si le mot « interstices » existe dans le texte du roman « Vingt mille lieues sous les mers » de Jules Verne. Dans cette situation, \(x\) est égal à « interstices » et \(E\) est composé de tous les mots qui apparaissent dans le roman.

Plusieurs méthodes peuvent être employées :

• Parcourir un par un tous les mots de \(E\) et les comparer à \(x\). En cas d’égalité répondre oui et s’arrêter. Si tous les mots sont parcourus, et que \(x\) n’a pas été trouvé, répondre non. Il existe de nombreux algorithmes pour accélérer ce type de recherche, le lecteur intéressé pourra se référer à l’excellent ouvrage de Christian Charras et Thierry Lecroq [voir la référence bibliographique 1].
• Utiliser un index. Nous connaissons ceux des livres de cuisine qui font le lien entre une recette et la page où elle est décrite. Eh bien en informatique l’index est une structure de données qui pré-traite l’ensemble \(E\), afin de savoir en temps constant (et rapide) si \(x\) existe (et éventuellement où), indépendant de la taille de \(E\). Il existe de nombreuses structures de données pour créer ce type d’index. On peut mentionner l’une des plus célèbres : la table de hachage, basée sur le hachage, dont le principe est décrit dans cet article Interstices, ou le filtre de Bloom que l’on va présenter dans cet article.

Hachage et collisions

La valeur de hachage d’un élément est un entier qui est obtenu en appliquant une fonction de hachage \(f\) sur cet élément. Par exemple, on peut simplement définir \(f\) par la somme des valeurs des lettres qui composent un mot (avec \(a\) qui vaut \(1\), \(b\) qui vaut \(2\), etc.). Dans ce cas \(f(\text{interstices})\) vaudrait \(141\).

def ascii_hash(mot): 
    hash = 0 
    for lettre in mot:
        hash += ord(lettre.lower()) - ord('a') + 1 
    return hash

mot = "interstices" 
valeur_hachage = ascii_hash(mot) 
print(f"La valeur de hachage de {mot} est {valeur_hachage}")

Ce morceau de code Python est une simple implémentation de la fonction de hash proposée.

Pour indexer, l’idée fondamentale est que la valeur de hachage associée à un élément détermine son adresse dans une structure de données (par exemple un simple tableau) et qu’elle permet d’indiquer son existence ou de lui associer des informations supplémentaires. C’est le cas des tables de hachage ou des filtres de Bloom, dont il est question ici.

Généralement, les fonctions de hachage sont sujettes aux collisions. C’est-à-dire que deux mots \(x\) et \(x’\) différents peuvent avoir la même valeur de hachage. Prenez par exemple \(x=\) « chien » et \(x’=\) « niche ». Ces deux mots sont composés des mêmes lettres, et leur valeur de hachage avec notre fonction \(f\) est la même (elle vaut \(39\)). Ces deux mots sont dits en collision pour notre fonction \(f\).

Par ailleurs, afin d’économiser de l’espace mémoire, le nombre d’adresses dans les tables de hachage ou les filtres de Bloom est limité. En pratique, le nombre d’adresses allouées, noté \(N\), est plus petit que le nombre de valeurs de hachage possibles. Ainsi, l’adresse d’un élément dans la structure est le modulo de la valeur de hachage par la taille de la structure. Formellement \(adresse(x) = f(x) \text{ modulo } N\). Cela veut simplement dire que si la structure comporte par exemple \(100\) adresses et que la valeur de hachage d’un élément est, disons, \(104\), alors on range cet élément à l’adresse \(4\). Ceci crée une nouvelle situation de collision où des mots distincts se retrouvent associés à la même adresse. Dans notre exemple, avec \(N=100\), les mots \(x\) et \(x’\) tels que \(f(x)=4\) et \(f(x’)=104\) seraient tous les deux associés à la même adresse \(4\).

Il existe donc deux situations qui amènent à des collisions d’adresses entre deux éléments distincts.

Par analogie on peut imaginer la valeur de hachage d’un élément comme son numéro de maison dans une rue. Les collisions reviennent à considérer que deux personnes différentes habitent à la même adresse dans la rue.

Tables de hachage

Sans entrer dans les détails, une table de hachage met en œuvre une solution pour détecter les collisions et les traiter. Avec une telle table, il est possible à la requête de faire la différence entre « chien » et « niche ». La solution revient à écrire sur la boîte aux lettres de chaque maison le nom de ses occupants présents. Si l’on sait que la maison est occupée, il suffit de lire les noms inscrits sur la boîte aux lettres pour savoir si celle que l’on cherche est bien là. Par exemple si je demande si Mme « Lovelace » habite dans la rue, je calcule d’abord son adresse avec notre fonction \(f\), ce qui nous donne la valeur \(75\), puis, si la maison n°75 est occupée, je vérifie que son nom apparaît effectivement sur la boîte aux lettres.

Une telle validation se fait au prix d’une utilisation importante de mémoire car il faut explicitement stocker tous les éléments indexés. Par exemple indexer 10 milliards de mots de taille 30 (valeurs usuelles en bio-informatique) nécessite près de 300 GB. Ceci limite son utilisation sur plusieurs milliards d’éléments car elle implique de gros besoins en termes de capacité de calculs.

Filtres de Bloom

À l’inverse d’une table de hachage, un filtre de Bloom ne gère pas les collisions. Dans cette situation, les maisons de notre rue n’ont pas de boîte aux lettres. Si la lumière est allumée, on sait qu’il y a au moins une personne qui s’y trouve, sinon elle est vide. Ainsi, si le numéro 75 est éteint, on est certain que Mme Lovelace n’est pas là, sinon on peut répondre qu’elle s’y trouve, mais on n’est pas certain qu’il s’agisse bien d’elle.

En pratique, un filtre de Bloom est un simple tableau \(T\) de \(N\) bits, tous initialement égaux à zéro (\(T[i]=0\) pour tout \(i\) entre \(0\) et \(N-1\)). Lors de la phase d’indexation, pour chaque élément à insérer, son adresse dans le tableau est calculée, et le bit correspondant à cette adresse est mis à \(1\) (on allume la lumière). Formellement, avec \(x\) l’élément à insérer, \(T[f(x) \text{ modulo } N] \leftarrow 1\). Notez que si plusieurs éléments différents ont la même adresse, le bit correspondant reste à \(1\) (on laisse la lumière allumée).

Lors de la requête, pour tester si un élément (appelé \(y\)) est présent, le filtre de Bloom indique si le bit correspondant à son adresse est égal à \(0\) ou \(1\).
S’il est égal à \(0\), alors \(y\) n’a pas été indexé et le filtre répond « non ».
S’il est égal à \(1\), le filtre répond « oui ». Dans ce cas il peut s’agir d’une bonne réponse : l’élément \(y\) avait effectivement été inséré. On parle alors de vrai positif. Il peut également s’agir d’une mauvaise réponse : le bit correspondant à son adresse avait été mis à \(1\) par un autre élément sans que l’élément \(y\) n’ait été inséré. On parle alors de faux positif.

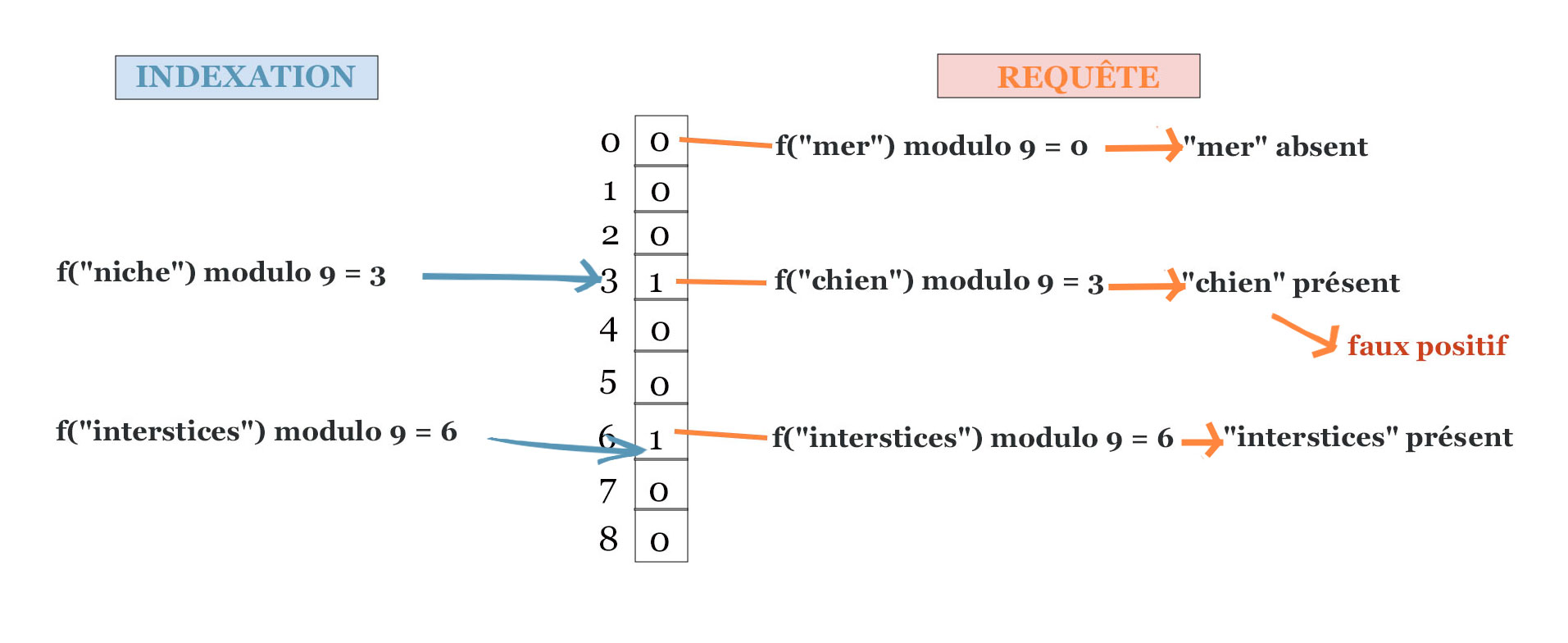
Exemple d’utilisation d’un filtre de Bloom pour indexer des mots. Un filtre ici composé de 9 bits, est initialisé avec les mots « niche » et « interstices ». Il est interrogé avec les mots « mer », « chien » et « interstices ».

Dans l’exemple représenté dans la figure précédente, nous avons créé un filtre de taille \(N=9\) et on y a inséré les deux éléments « niche » et « interstices », respectivement aux adresses 3 et 6. Nous avons requêté le mot « mer », dont l’adresse est \(f(\text{« mer »}) \text{ modulo } N\) qui vaut \(36\) modulo \(9\), c’est-à-dire \(0\). La valeur associée (\(T[0]\)) est égale à zéro. Il est donc certain que « mer » ne fait pas partie des mots indexés. On a également requêté le mot « interstices », dont l’adresse est 6, associée à un bit à un. Dans ce cas le filtre répond « oui », et il s’agissait bien d’un vrai positif, car le mot « interstices » avait été indexé. Le troisième mot requêté est « chien », qui n’avait pas été indexé, mais qui a la même adresse que « niche » égale à \(3\). Dans ce cas le filtre se trompe car \(T[3]\) vaut \(1\). Il s’agit d’un faux positif.

Du fait de la présence de faux positifs, les filtres de Bloom sont utilisés, comme leur nom l’indique, pour filtrer des requêtes afin de limiter un espace de recherche, c’est le cas par exemple dans les applications réseaux, ou pour estimer des similarités entre jeux de données, comme par exemple en bio-informatique.

Le filtre de Bloom ne se compose que du tableau de bits (dans la figure précédente il s’agit de \(000100100\)). Il est donc impossible lors de la requête de faire la différence entre un faux positif et un vrai positif. On définit le taux de faux positifs d’un filtre de Bloom par le ratio de réponses incorrectes lorsque l’on ne requête que des éléments négatifs.

Il y a deux façons de limiter le taux de faux positifs d’un filtre de Bloom.

• Il est possible d’utiliser plusieurs (disons \(z \geq 2\)) fonctions de hachages distinctes pour chaque élément. Dans ce cas lors de l’indexation, \(z\) adresses sont calculées et les \(z\) bits correspondant sont mis à \(1\). Lors de la requête, un élément est considéré comme présent seulement si tous ses \(z\) bits sont égaux à \(1\). Ceci multiplie les temps de calculs par \(z\), et en augmentant \(z\) on augmente aussi la quantité de bits à ‘\(1\)’ dans le filtre, ce qui finit par conduire à une saturation et in fine à une augmentation du taux de faux positifs.
• L’autre possibilité est bien entendu d’utiliser un filtre le plus grand possible au prix de l’utilisation de plus d’espace. Ceci conduit à limiter le nombre d’éléments ayant la même adresse.

Il existe un service web qui permet de calculer et visualiser le rapport entre la taille du filtre, le nombre d’éléments insérés, le nombre de fonctions de hachage, et le taux de faux positifs [voir la référence 2]. En résumé, les filtres de Bloom offrent une solution permettant de connaître l’appartenance d’un élément à un ensemble, au prix de la présence de faux positifs. De par leur simplicité et le fait qu’ils ne nécessitent pas de stocker les éléments de l’ensemble, ils sont utiles pour passer à l’échelle sur de très gros jeux de données. Par exemple, avec une unique fonction de hachage, pour indexer \(10\) milliards d’éléments avec environ \(10\) % de faux positifs, il faut utiliser \(N\) égal à \(100\) milliards de bits ce qui représente approximativement \(11\) gigaoctets. Si cette taille est acceptable pour indexer un jeu de données, elle devient inadaptée lorsqu’il s’agit d’en indexer des milliers (avec un filtre de Bloom par jeu de données).

Astuce pour limiter le taux de faux positifs pour indexer des données génomiques

Quand on cherche à indexer des données génomiques, les mots que l’on souhaite indexer sont tous de la même taille, notée \(k\). Ces mots sont appelés des k-mers (cf l’article « Analyser les génomes des océans »). Pour simplifier la lecture, les exemples qui suivent utilisent de toutes petites valeurs de \(k\). En pratique les outils bio-informatiques utilisent des valeurs comprises entre \(30\) et \(100\). Pour limiter le taux de faux positifs lors de l’indexation de k-mers il est possible d’utiliser une astuce basée sur l’idée suivante :

• Si un k-mer est présent dans un texte, alors tous ses mots de taille plus petite (notée \(s\)) sont également présents dans le texte.
• Inversement, si au moins un des mots de taille \(s\) qui compose un k-mer est absent d’un texte, alors le k-mer est également absent du texte.

Par exemple, si l’on sait que le mot « ACT » n’est pas dans un texte, alors on sait également que le mot « GACTG » est également absent. En pratique, on utilise cette astuce en insérant dans le filtre de Bloom tous les mots de taille \(s\) d’un texte à indexer (appelés des s-mers). Lors de la requête, ce sont bien des k-mers (avec \(k\geq s\)) qui sont requêtés, mais ce sont les s-mers qui sont indexés. Pour requêter un k-mer, on requête tous ses s-mers. S’ils sont tous indexés, alors nous répondons « oui ». Si l’un d’entre eux est absent, alors on est certain que le k-mer n’était pas dans le texte indexé, donc nous répondons « non ».

Par exemple avec \(k=5\) et \(s=3\), si l’on souhaite requêter le mot « GACTG », on teste tous ses s-mers (« GAC », « ACT », et « CTG »). Il y a \(k-s+1\) s-mers dans un k-mer. Cette astuce a été proposée dans une méthode, appelée findere [voir la référence 3]. Comparée à un filtre de Bloom original, ses avantages sont :

• Un taux de faux positifs très faible : pour qu’un k-mer soit un faux positif, dans le cas général, il est nécessaire que tous ses s-mers le soient également. Le taux de faux positifs décroît donc exponentiellement avec le nombre de s-mers requêtés par k-mer. Par exemple si on fait en sorte de requêter \(5\) s-mers par k-mer, avec un filtre de Bloom dont le taux de faux positifs est de \(10\) % (\(0.1\)), alors, avec cette approche, le taux de faux positifs effectif sur les k-mers est de \(0.1^5\), c’est-à-dire \(0.001\) %.
• Une requête plus rapide : l’utilisation habituelle requête tous les k-mers successifs d’un texte. Lorsque l’on passe d’un k-mer (exemple GACTG) à son voisin immédiat (ACTGA), il n’y a qu’un seul nouveau s-mer à requêter. Ceci est représenté sur les deux premiers k-mers requêtés dans la figure suivante. Dans ce cas, hormis pour la requête du premier k-mer, le temps de calcul est le même avec ou sans findere (un unique accès au tableau du filtre de Bloom par k-mer requêté). La situation devient favorable à findere dès lors qu’un s-mer est détecté absent. Dans ce cas, on sait alors que tous les k-mers qui le chevauchent sont également absents et il n’est pas nécessaire d’en requêter les s-mers. C’est le cas du s-mer représenté en rouge sur la figure suivante !

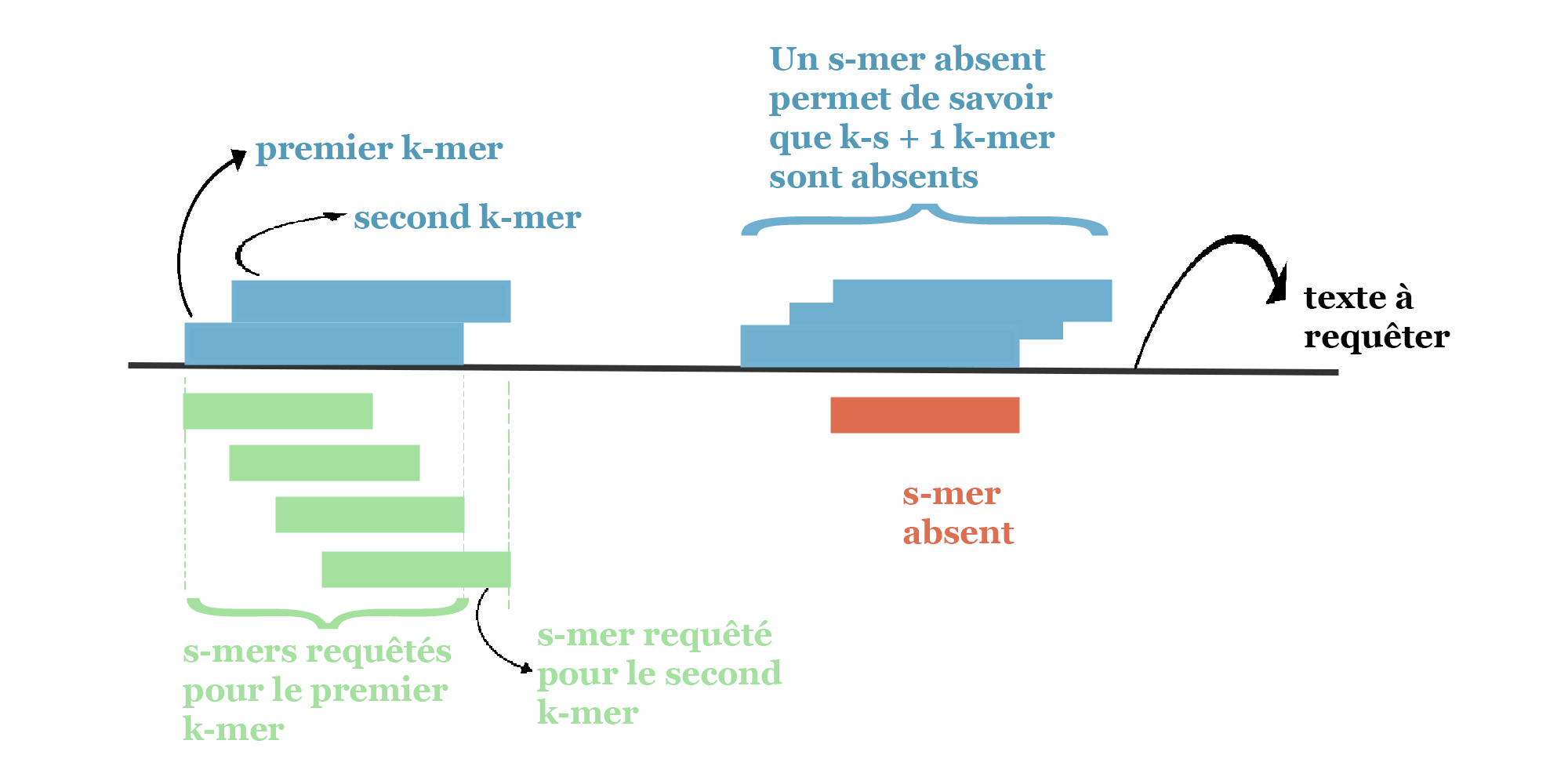
Exemple de requêtes de k-mers successifs avec findere. Ici la présence d’un k-mer (rectangles bleus) est vérifiée via tous ses 3 s-mers (rectangles verts). À droite un s-mer est absent de l’index (s-mer rouge). Tous les k-mers qui le chevauchent sont donc absents du texte indexé.

Le désavantage de cette méthode est qu’elle peut conduire à la création d’un nouveau type de faux positifs. Un k-mer absent (« ACCAG » par exemple) peut être composé uniquement de s-mers présents (« ACC », « CCA », « CAG ») dans d’autres k-mers. Dans ce cas, cette méthode considère à tort que « ACCAG » est présent car tous ses s-mers le sont aussi. Avec les valeurs usuelles de \(s\) (au moins égal à \(20\)) et les valeurs usuelles de \(k\) (généralement autour de \(30\)) ce type de faux positif est très rare.

Au final, l’approche findere permet d’accélérer les temps de requête et de diminuer de plusieurs ordres de grandeur le taux de faux positifs d’un filtre de Bloom lors de l’utilisation pour des mots de taille fixe. Sans utiliser findere, l’index proposé sur les données Tara Oceans décrit dans cet article aurait pris \(35\) fois plus d’espace. Nous n’aurions simplement pas pu le stocker.

Ces travaux ont été financés par le projet ANR SeqDigger (ANR-19-CE45-0008) ainsi que par le Défi Inria OmicFinder.