
Au-delà de Fourier, un monde qui vibre
L’analyse de Fourier repose sur une idée éblouissante : représenter « toute » fonction comme superposition de sinus et de cosinus. Considérons par exemple une mesure \(M(t)\) d’une grandeur physique qui varie au cours du temps \(t\). Grâce à Fourier, ce signal peut être décomposé en « somme » de sinus et cosinus, de la forme \(S(f) \sin(2 \pi f t)\) ou \(S(f) \cos(2 \pi f t)\), c’est-à-dire d’ondes d’amplitude \(S(f)\) oscillant indéfiniment à la fréquence \(f\) (donc avec une période \(T=1/f\)). Ce sont des ondes monochromatiques, comme les vibrations lumineuses oscillant à une seule fréquence, qui fixe la couleur.
Lorsqu’on est confronté à cette idée pour la première fois, il y a là quelque chose qui a de quoi surprendre, même si le caractère au fond très simple de ce résultat lui donne un sens intuitif. En effet, sans aller jusqu’à dire que tout est ondes et vibrations, force est de constater que, de l’infiniment grand à l’infiniment petit, du mouvement des planètes aux atomes, en passant par l’électromagnétisme ou l’acoustique et jusqu’aux rythmes biologiques ou la rotation des machines, les oscillations sont omniprésentes dans le monde qui nous entoure.
La phrase célèbre de Fourier, selon laquelle « l’observation de la nature est la source la plus féconde des découvertes mathématiques », prend ainsi un tour particulièrement pertinent.
D’un point de vue mathématique, la force du résultat de Fourier est qu’une décomposition en ondes monochromatiques reste possible pour des situations à la fois plus générales et presque quelconques, comme des signaux non périodiques, voire du « bruit ». Ainsi, une oscillation transitoire peut se décrire « à la Fourier » en superposant un grand nombre d’oscillations de toutes fréquences, mais toutes établies dans le temps de façon permanente, c’est-à-dire depuis le passé le plus lointain jusqu’à l’avenir le plus éloigné, donc y compris en dehors du support de l’oscillation transitoire. La prouesse mathématique de cette représentation s’accompagne ainsi d’une limitation d’interprétation physique, les valeurs nulles du signal en dehors du support du transitoire résultant d’une compensation d’oscillations qu’il faut bien reconnaître comme virtuelles, sans existence réelle.
Les deux animations ci-dessous sont présentées de la même façon. Le signal mesuré \(M(t)\) est tracé en noir en bas, avec le temps qui augmente de gauche à droite. Le spectre, c’est-à-dire les amplitudes \(S(f)\), est tracé en rouge en haut, avec la fréquence qui augmente de gauche à droite, des basses aux hautes fréquences.
La vidéo montre la reconstruction du signal en balayant les fréquences et en superposant les modes de Fourier. Le mode de Fourier \(S(f) \sin(2 \pi f t)\) ou \(S(f) \cos(2 \pi f t)\) qui participe à la reconstruction est tracé au milieu en bleu. Il est ajouté au signal en cours de reconstruction, qui est tracé en bleu au-dessus du signal noir \(M(t)\). Peu à peu, le signal reconstruit devient identique au signal de départ, après avoir exploré toutes les fréquences.
Le processus est illustré sur deux situations différentes du point de vue de l’interprétation physique.
Dans la première situation (ci-après), le signal semble varier beaucoup au cours du temps, mais il correspond au modèle de Fourier car il est explicitement constitué de la superposition de 3 oscillations sinusoïdales. Son spectre montre en effet trois pics qui sont les trois modes de Fourier qui contribuent le plus dans la superposition. Alors que le signal est étalé dans le temps, le spectre est condensé autour de trois fréquences. Le signal est bien reconstruit en ajoutant ces trois modes.
Dans la deuxième situation (ci-après), le signal est transitoire : il vaut zéro sauf pendant un bref intervalle de temps où il oscille durant deux périodes. Son spectre occupe toutes les fréquences : les valeurs \(S(f)\) sont quasiment toutes non nulles. C’est la situation inverse de la première vidéo: le signal est condensé dans le temps et le spectre est étalé en fréquence. Le signal n’est bien reconstruit qu’en balayant toutes les fréquences. C’est la superposition de tous les modes de Fourier qui annule le signal reconstruit en-dehors du bref intervalle de temps.
Ces deux vidéos illustrent la dualité temps-fréquence d’un signal et un principe d’incertitude : un signal infiniment court (une impulsion) a un spectre infiniment étendu (toutes les fréquences y contribuent), tandis qu’une fréquence pure (un spectre constitué d’une seule raie) est associée à un signal de durée infinie.
Fourier musicien
Réconcilier physique et mathématique a donné lieu depuis une cinquantaine d’années à de nombreux travaux pour développer des méthodes s’attachant à dépasser cette limitation d’interprétation. Pour reprendre l’exemple de l’oscillation transitoire, on peut voir cette dernière comme l’idéalisation très simplifiée d’une note de musique dont la fréquence fixe la hauteur et l’amplitude le niveau sonore, avec une localisation dans le temps permettant de connaître la durée de la note en question et de savoir quand elle apparaît dans un morceau. En ce sens, aller « au-delà de Fourier » revient à écrire la partition d’un signal, en ne choisissant plus de façon exclusive entre temps et fréquence pour sa représentation, mais en le déployant conjointement sur les deux variables sous la forme d’une représentation temps-fréquence, à l’image d’une portée musicale devenue mathématique.
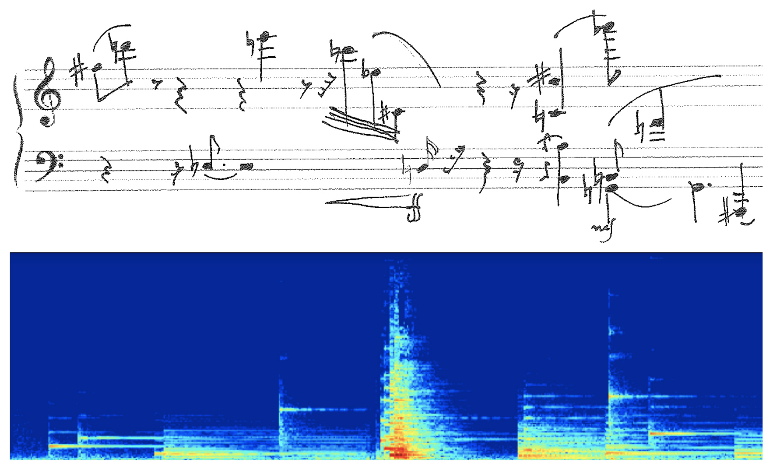
Interprétation musicale d’une représentation temps-fréquence : spectrogramme.
En haut : partition d’une pièce pour piano.
En bas : résultat d’une analyse de Fourier à court terme du signal sonore correspondant, avec le temps en abscisse, la fréquence en ordonnée et l’intensité codée en fausses couleurs (du bleu profond pour les faibles valeurs au rouge pour les plus grandes). L’intensité est calculée à partir du spectre et des ondes sinus et cosinus dans la transformation de Fourier. Cette représentation est appelée un spectrogramme.
À bien y réfléchir, ce point de vue peut sembler très naturel, mais il a en fait donné lieu à une activité intense pour lui attribuer un sens précis et lui associer des algorithmes de calcul efficaces permettant d’en banaliser l’usage.
Fourier local et ondelettes
La façon de faire la plus simple et la plus répandue consiste à calculer la transformée de Fourier de façon locale, en restreignant l’analyse à une fenêtre d’observation de support réduit, glissant dans le temps : c’est ce que l’on appelle une transformée de Fourier à court terme et c’est ainsi qu’a été obtenu le spectrogramme ci-dessus. Cette approche repose cependant sur l’arbitraire du choix de la fenêtre « à court terme » utilisée, et en particulier de sa durée. Celle-ci conditionne la plage des fréquences obtenue dans la transformée de Fourier à court terme. Pour bien localiser en temps l’intensité d’un signal, il faut une durée courte ; par contre, il faut une durée longue pour bien localiser en fréquence l’intensité. On retrouve le principe d’incertitude évoqué plus haut.
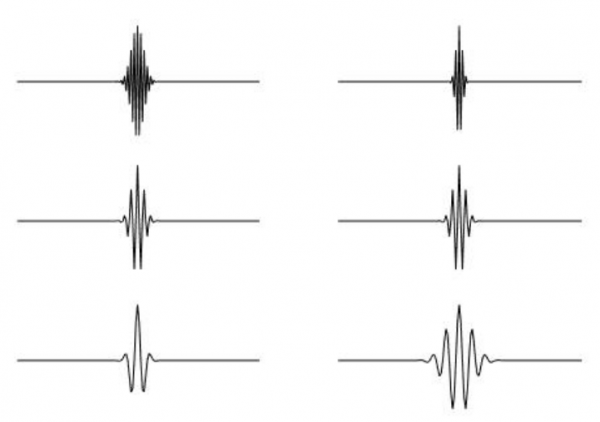
Notes de Fourier et ondelettes.
Dans une transformation locale, on utilise une superposition de paquets d’ondes, d’une fréquence donnée, qui sont nuls en dehors de la fenêtre d’observation. Dans la transformation de Fourier à court terme (à gauche), les « notes de Fourier » ont une durée indépendante de la fréquence (haute fréquence en haut et basse fréquence en bas). Dans la transformation en ondelettes (à droite), la durée diminue avec la fréquence: l’ondelette est d’autant plus brève que la note est plus aiguë (haute fréquence) et d’autant plus longue qu’elle est grave (basse fréquence).
Quelle que soit la méthode employée, il ne sera jamais possible de battre en brèche cette limitation qui interdit de connaître de façon infiniment précise la fréquence d’un signal à un instant donné, mais il est possible d’en contrôler les effets par des variantes ou des alternatives à l’analyse de Fourier à court terme. Ainsi, plutôt que de fixer la durée d’une fenêtre, on peut choisir de fixer le nombre d’oscillations analysables à l’intérieur de celle-ci. De cette façon, une fréquence basse (un son grave) est analysée avec une fenêtre de plus longue durée qu’une fréquence élevée, celle-ci ne nécessitant qu’une durée courte (cf. représentation ci-dessus).

Yves Meyer. Photo © B. Eymann – Académie des sciences.
L’analyse résultante, appelée transformation en ondelettes, a connu depuis son introduction dans les années quatre-vingts un développement considérable allant au-delà d’une forme modifiée d’analyse temps-fréquence et culminant avec l’attribution du prestigieux Prix Abel à Yves Meyer (photo de droite), l’un des pères fondateurs des ondelettes, en 2017.
Science et technologie
Ces approches conjointes, qui innovent tout en restant dans la filiation naturelle des idées de Fourier, sont aujourd’hui omniprésentes dans la plupart des domaines de la science et de la technologie.
C’est le cas en particulier en audio (parole, musique) où l’on retrouve des variantes de l’analyse de Fourier à court terme dans la plupart des approches couramment utilisées, qu’il s’agisse de codage (MP3), d’analyse, de synthèse, de reconnaissance (Shazam®) ou encore de transcription. Une des raisons à cela est la nature même des systèmes humains de phonation et d’audition. À l’émission, la production d’un signal vocal résulte essentiellement de l’excitation de résonateurs variant dans le temps et, à la réception, l’oreille interne se comporte en première approximation comme un banc de filtres dont l’excitation sélective envoie au cerveau des informations fréquentielles évolutives. Dans les deux cas, c’est bel et bien un cadre mixte en temps et en fréquence qui s’avère naturel pour représenter ou coder l’information utile. Pour justifier ce dernier point relatif au codage, on peut revenir au spectrogramme (image ci-dessus) et noter qu’une part importante de l’intensité a pour couleur le bleu profond qui est représentatif de valeurs nulles ou très faibles. Ainsi, la transformée de Fourier à court terme concentre l’information sur un petit nombre de coefficients significatifs (les intensités d’une autre couleur que le bleu profond) qui suffisent à la coder (voir l’article à venir de Gaël Richard sur les représentations audio).
Si l’on se tourne maintenant du côté des images, c’est aussi une forme particulière d’analyse de Fourier locale qui est à l’œuvre dans le standard JPEG, celui que l’on retrouve dans la quasi-totalité des appareils photo grand public. Sans compression, une photo ordinaire « pèserait » plusieurs dizaines de mégaoctets, ce qui donnerait à son stockage, sa manipulation et sa transmission un coût prohibitif. La solution adoptée par le codage JPEG repose, tout comme en audio, sur une idée de parcimonie — c’est-à-dire utiliser le plus petit nombre possible de paramètres ou de descripteurs pour représenter une grandeur — dans l’espace de Fourier considéré localement. Plus précisément, l’image complète est découpée en petits blocs de 8×8 pixels auxquels est appliquée une forme modifiée de transformation de Fourier bidimensionnelle (la DCT, pour Discrete Cosine Transform). Il s’agit donc de nouveau d’une analyse de Fourier locale, cette fois en espace et non plus en temps. Tout comme avec la représentation temps-fréquence, seuls quelques coefficients de Fourier sont en général significatifs pour chaque bloc, réduisant d’autant le « poids » de l’image ainsi codée, qui peut descendre à quelques centaines de kilo-octets pour une qualité de reconstruction acceptable. Si l’on devient très exigeant sur la compression, la reconstruction de l’image à partir de trop peu de coefficients de Fourier locaux fait cependant apparaître des effets de blocs qui font écho à la découpe initiale. Pour pallier cette limitation, une alternative est possible en remplaçant l’analyse de Fourier locale par une décomposition en ondelettes globale. La raison en est que celle-ci possède une structure intrinsèquement multirésolution, considérant la richesse d’une image comme faite d’approximations et de raffinements par l’ajout de détails. Ce faisant, les effets de blocs n’ont plus de raison d’être et, à qualité égale, ceci permet d’atteindre des taux de compression sensiblement plus élevés que JPEG. Le standard correspondant est appelé JPEG2000 et est surtout utilisé dans des applications professionnelles (imagerie médicale, cinéma numérique HD) qui sont par nature plus exigeantes que, par exemple, des partages de photos-souvenirs sur les réseaux sociaux (voir l’article à venir de Christine Guillemot sur les codages JPEG et MPEG).
À côté de ces applications de nature technologique, l’analyse temps-fréquence joue un rôle important dans de nombreux problèmes de science plus fondamentale. Pour ne prendre qu’un exemple emblématique, elle offre un cadre de description pour les signaux d’ondes gravitationnelles récemment détectés par la collaboration LIGO-Virgo. Ces signaux entrent dans la classe de ce que l’on appelle des chirps, c’est-à-dire que, à la différence d’une onde de Fourier qui est monochromatique, leur fréquence varie au cours du temps (à l’image d’un sifflement modulé). Pour comprendre pourquoi les ondes gravitationnelles se manifestent par des chirps, il faut revenir à leur origine et à la possibilité de leur détection sur Terre. Autrement dit, la propagation d’une onde gravitationnelle se manifeste par une modification locale de l’espace-temps. Une façon de détecter son passage est alors de faire usage d’un interféromètre dont les bras, subissant un effet différentiel, conduisent à une figure d’interférences oscillante. Une onde gravitationnelle est cependant extrêmement ténue et seuls des événements astrophysiques particulièrement violents sont susceptibles de donner lieu à des oscillations observables sur Terre. C’est le cas des systèmes binaires formés d’objets très massifs comme des trous noirs ou des étoiles à neutrons. Dans ce scénario, les objets orbitent l’un autour de l’autre et, en rayonnant l’énergie portée par l’onde gravitationnelle qu’ils émettent, ils se rapprochent tout en tournant de plus en plus vite pour des raisons de conservation des lois du mouvement, jusqu’à l’instant où ils s’effondrent en un objet unique. L’interféromètre voit ainsi passer une onde dont la fréquence s’accélère, et la mesure des oscillations de la figure d’interférences se traduit par un chirp. Ce scénario longtemps resté hypothétique, faute d’instruments assez puissants, a été observé pour la première fois le 14 septembre 2015 par la collaboration LIGO-Virgo. La figure ci-dessous présente le chirp gravitationnel correspondant, enregistré à Hanford (Washington), ainsi que sa signature temps-fréquence obtenue par une forme modifiée d’analyse de Fourier à court terme (un spectrogramme réalloué permettant d’accroître la localisation). On observe ainsi une trajectoire reflétant l’augmentation de la fréquence au cours du temps, sa forme précise permettant en outre d’atteindre des paramètres physiques du système binaire, formé en l’occurrence de deux trous noirs d’une trentaine de masses solaires chacun.
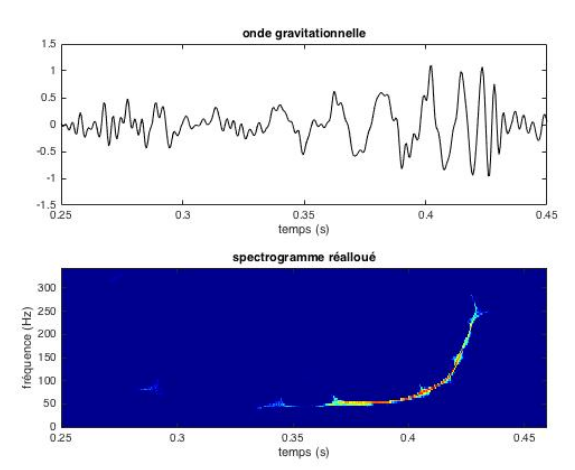
Onde gravitationnelle.
En haut : signal enregistré le 14 septembre 2015 à la sortie de l’interféromètre LIGO de Hanford (Washington).
En bas : résultat d’une analyse de Fourier à court terme modifiée de ce signal, permettant de maximiser la localisation sur la trajectoire de la fréquence instantanée. Quoique bruitée, la forme d’onde représentée dans le diagramme du haut met en évidence une oscillation s’accélérant au cours du temps, ce qui caractérise un chirp. L’image temps-fréquence précise la structure de ce chirp en permettant de visualiser la loi d’évolution de la fréquence au cours du temps sous la forme d’une trajectoire dans le plan.
Perspectives
L’analyse temps-fréquence est un champ de recherche toujours vibrant. La mise en œuvre des nombreuses méthodes existantes, dont seules quelques-unes ont été évoquées ici, a donné lieu au développement de boîtes à outils logicielles (voir par exemple la boîte à outils Temps-Fréquence, avec quelques démonstrations permettant de se familiariser à l’usage de techniques simples allant « au-delà de Fourier » tout en restant dans la ligne de sa vision scientifique, Fourier qui rappelait le devoir d’être « conduit jusqu’aux dernières applications numériques, condition nécessaire de toute recherche, et sans laquelle on n’arriverait qu’à des transformations inutiles. »).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Patrick Flandrin