Comment découper le gâteau ? Ou la répartition équitable de ressources

– « On t’a dit trois parts, Obélix ».
– « Eh bien, j’ai coupé trois parts! »

Dans un extrait culte de la BD Astérix et Cléopâtre, Obélix découpe en trois parts le gâteau empoisonné. Et même si Obélix fait sourire en découpant trois parts de tailles fort différentes, ses deux compagnons trouvent finalement acceptable la différence de taille des parts, car Astérix et Panoramix ont des parts largement suffisantes pour leurs appétits.

Figure 1 : Les trois parts de gâteau selon Obélix. Image extraite de la BD « Astérix & Obélix : Mission Cléopâtre ».

En effet, au moment de partager un gâteau, la question n’est pas de faire des parts de tailles égales, mais bien que chacun considère que la répartition proposée correspond à son envie, tout en respectant une certaine notion d’équité.

Mais quand un gâteau est hétérogène, par exemple avec des particularités qui différencient les parts (fruits ou chocolat répartis différemment, brûlé d’un côté…), cela devient plus difficile de faire un algorithme de partage équitable. La découpe de gâteau peut être vue comme un jeu dont les gourmands sont des joueurs qui essaient d’avoir une part qui les satisfait… et même un peu plus : en effet, c’est tout l’intérêt d’un jeu que de tenter d’avoir la meilleure part du gâteau ! Pour cela, chacun tait ce qu’il juge satisfaisant pour lui, de peur de n’avoir que cela à manger et rien de plus. Ce petit plus qui fait toute la saveur du jeu… et du gâteau.

Découper un gâteau avec deux joueurs

Dans un premier temps, on considère deux joueurs et une forme d’équité bien classique appelée le partage proportionnel et qui peut se définir ainsi : chaque joueur sait ce qu’il aime et peut attribuer une valeur à chaque part possible du gâteau. Mais cette évaluation dépend du joueur : l’un aimera la part avec plus de fraises et l’autre la part avec plus de framboises. Un partage est proportionnel si chaque joueur a une part qu’il estime être au moins la moitié de sa propre évaluation totale du gâteau.

À deux joueurs, l’algorithme folklorique pratiqué très couramment est je partage, tu choisis. Le premier joueur partage le gâteau en deux parts qui, de son point de vue, ont la même valeur. Et c’est le deuxième joueur qui choisit la part qu’il préfère. Si le premier joueur crée une part qu’il estime à moins de la moitié de la valeur totale du gâteau… il risque de se la voir attribuer par le deuxième joueur. Il découpe donc honnêtement le gâteau. Le deuxième joueur peut considérer que les parts n’ont pas la même valeur de son point de vue. Mais pourtant ce partage est bien proportionnel : comme le gâteau est coupé en deux parts seulement, il y a une des parts qui est au moins la moitié de ce qu’il estime être la valeur totale du gâteau ; il prend alors cette part. Et comme dit plus haut, l’autre part est suffisante pour le premier joueur.

On peut noter que le partage proportionnel obtenu n’est pas totalement satisfaisant. En effet ce partage n’est pas égalitaire : le premier joueur a exactement ce qu’il juge satisfaisant (la moitié de la valeur totale pour lui), mais le second obtient une part qui vaut éventuellement plus que la moitié du gâteau de son point de vue. Il vaut donc mieux être le deuxième joueur avec cet algorithme ! (On peut proposer facilement un partage symétrique et donc plus égalitaire, voir plus loin l’encart 1 sur le partage symétrique à deux joueurs).

En pratique, le « gâteau » peut être de différentes natures. Il peut être spatial lorsqu’il s’agit de partager des terres : par exemple, dans la Bible, Abraham choisit le point de partage et Loth choisit le côté de terre qui lui sera attribué. Des algorithmes similaires sont décrits pour l’attribution des zones minières dans les océans internationaux dans la Convention des Nations Unies sur le droit de la mer annexe III, article 8 : « le demandeur indique les coordonnées permettant de diviser la zone en deux parties de valeur commerciale estimative égale ». Le gâteau peut être temporel lorsqu’il s’agit de partager le temps disponible d’une unique prise pour recharger des téléphones, ou celui d’un satellite entre des requêtes d’observation de la Terre pour différents financeurs (publics, militaires, privés).

Découper un gâteau pour trois joueurs (et plus !)

On considère ici \(n\) joueurs gourmands qui doivent se partager un gâteau qui est hétérogène : par exemple, il contient du chocolat noir, du chocolat blanc et du chocolat au lait comme sur la figure 2 ci-dessous. Le gâteau est un cake rectangulaire que l’on voit de côté et qui a ainsi un tiers chocolat noir, un tiers chocolat blanc et un tiers chocolat au lait. On fait l’hypothèse qu’une part de gâteau est un intervalle sur le côté du gâteau.

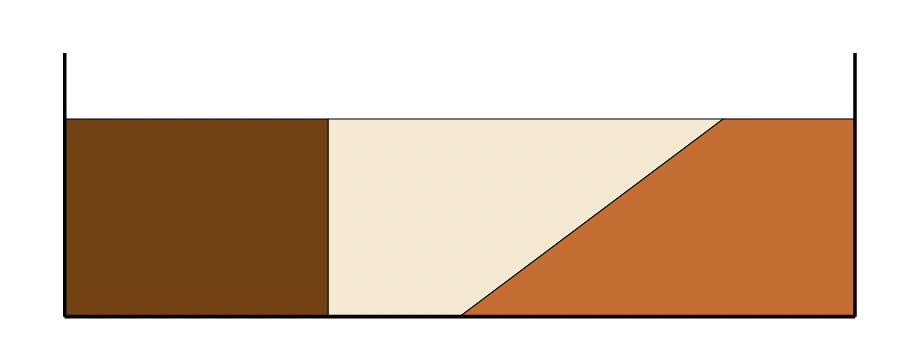
Figure 2 : Le gâteau hétérogène au chocolat.

Pour jouer et avoir une part la plus satisfaisante possible, chaque joueur garde cachées ses préférences sur le gâteau. Et ces préférences sont éventuellement différentes d’un joueur à l’autre. Par exemple, Alice aime le gâteau et n’a pas de préférence sur le chocolat ; Bob n’aime que le chocolat noir ; Camille aime deux fois plus le chocolat noir que le chocolat au lait et n’aime pas trop le chocolat blanc (elle n’aimerait pas avoir une part n’ayant que du chocolat blanc par exemple !).

Sur la figure 3 ci-dessous, le gâteau est partagé en trois parts de taille identique. Bob qui préfère le chocolat noir a la part avec du chocolat noir, Camille qui préfère le chocolat au lait au chocolat blanc a la troisième part et Alice, qui est indifférente, a la part du milieu. Si Bob et Alice sont satisfaits d’avoir un tiers du gâteau selon leurs préférences, Camille a-t-elle une part selon ses vœux ? En effet, de son point de vue, sa part vaut moins que le tiers du gâteau. Un autre découpage pourrait être rendu plus équitable en étant proportionnel.

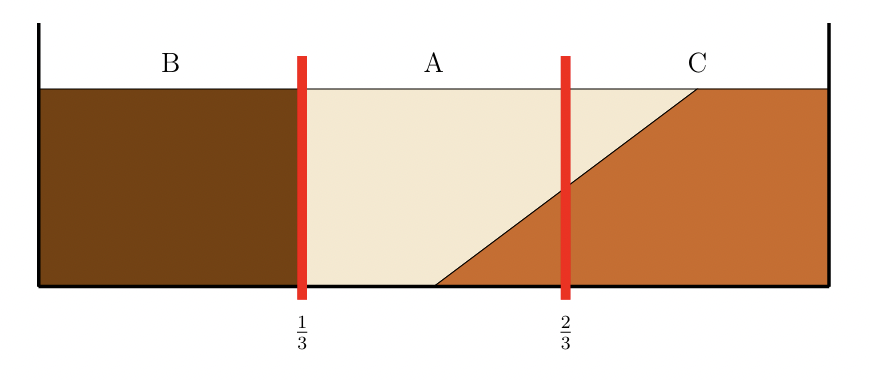
Figure 3 : Partage du gâteau en trois parts de même taille.

Regardons le partage de la figure 4 ci-dessous. Bob a eu une petite part en taille mais il a un tiers de la partie chocolat noir : comme le reste du gâteau ne l’intéresse pas, il peut juger cela équitable selon sa propre évaluation ! Alice a toujours un tiers du gâteau et cela peut aussi lui sembler équitable. Camille a eu une grosse part qui peut compenser le fait qu’elle n’ait pas eu de chocolat noir ! Ce partage peut sembler proportionnel car chaque joueur considère peut-être que sa part vaut au moins un tiers du gâteau.

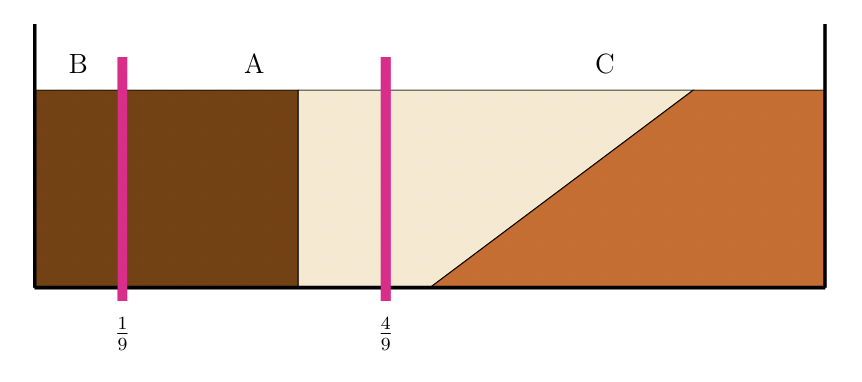
Figure 4 : Un autre partage du gâteau.

Modélisons !

Afin de pouvoir définir proprement les goûts de chacun, et aussi pour manipuler ces notions, modélisons les goûts et le partage mathématiquement. On note \(N\) l’ensemble des \(n\) joueurs qui doivent se partager un gâteau représenté par l’intervalle \([0,1]\) (beaucoup de formes de gâteau peuvent être représentées par un intervalle, et pas seulement les cakes !). Chaque joueur \(i\) possède une fonction d’évaluation \(V_i\) sur les intervalles \(I \subseteq [0,1]\). On note \(V_i(x,y)\) la valeur que le joueur \(i\) attribue à l’intervalle \([x,y]\). On fait quelques hypothèses (réalistes) sur ces fonctions d’évaluation :

• afin de pouvoir comparer les valeurs du gâteau pour les différents joueurs, on normalise la valeur du gâteau total à 1 pour tous les joueurs : \(\forall i\in N, V_i(0,1)=1\) ;
• chaque part du gâteau est désirable pour chaque joueur (non-négativité) : \(\forall I \subseteq [0,1], V_i(I)\geq 0\) ;
• les fonctions d’évaluation sont divisibles : \(\forall i\in N, \forall x,y\in [0,1]\) et \(\forall \ 0\leq \lambda \leq 1\), \(\exists z \in [x,y]\) tel que \(V_i(x,z)=\lambda V_i(x,y)\). C’est-à-dire que pour toute part de gâteau (délimitée ici par \(x\) et \(y\)), et pour toute proportion \(\lambda\) entre 0 et 1, il existe un découpage en deux parts dont la part de gauche (entre \(x\) et \(z\)) vaut \(\lambda\) fois la part complète (entre \(x\) et \(y\)).

Les figures 5, 6 et 7 proposent des exemples de fonction d’évaluation pour le gâteau de la figure 2 : la valeur \(V_i\) d’une part de gâteau, représentée par un intervalle, correspond à l’aire sous la courbe sur cet intervalle. La fonction d’évaluation la plus simple est la fonction \(V_A\) d’Alice car elle n’a pas de préférence sur le chocolat. Elle est représentée par l’aire sous la courbe bleue de la figure 5 : c’est directement la longueur de l’intervalle fois 1, soit \(V_A(x,y)=y-x\).

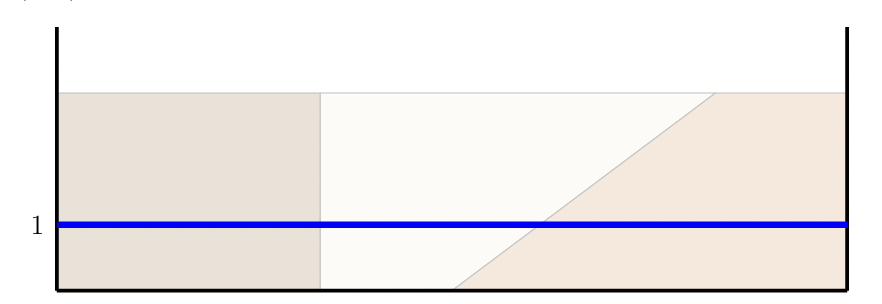
Figure 5 : L’aire sous la courbe donne la fonction d’évaluation \(V_A\) d’Alice

Pour Bob, toute la valeur du gâteau réside dans la partie contenant du chocolat noir qui représente un tiers du gâteau. La fonction d’évaluation \(V_B\) de Bob est donc donnée par l’aire sous la courbe jaune de la figure 6. Et ainsi \(V_B\left(0,\frac{1}{3}\right)=1\) (et donc \(V_B\left(\frac{1}{3},1\right)=0\)). On peut donc noter par exemple que \(V_B\left(0,\frac{1}{9}\right)=\frac{1}{3}\) : ce qui signifie qu’un neuvième (bien situé) du gâteau donne une part acceptable pour Bob dans un partage proportionnel.

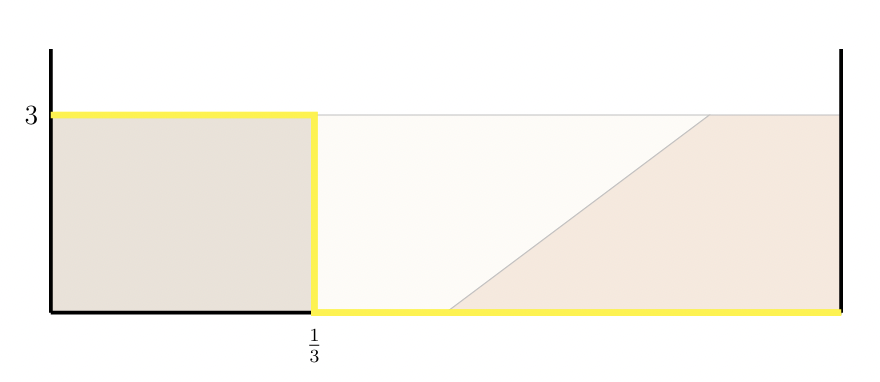
Figure 6 : L’aire sous la courbe donne la fonction d’évaluation \(V_B\) de Bob.

Enfin la fonction d’évaluation \(V_C\) de Camille est plus complexe. Par la fonction donnée par l’aire sous la courbe verte de la figure 7, on peut lire que Camille aime deux fois plus le chocolat noir que le chocolat au lait. En effet, \(V_C\left(0,\frac{1}{3}\right)=\frac{2}{3}\) et \(V_C\left(\frac{1}{2},1\right)=\frac{1}{3}\). D’autre part elle n’aime pas trop le chocolat blanc et n’en veut que s’il est collé à du chocolat au lait.

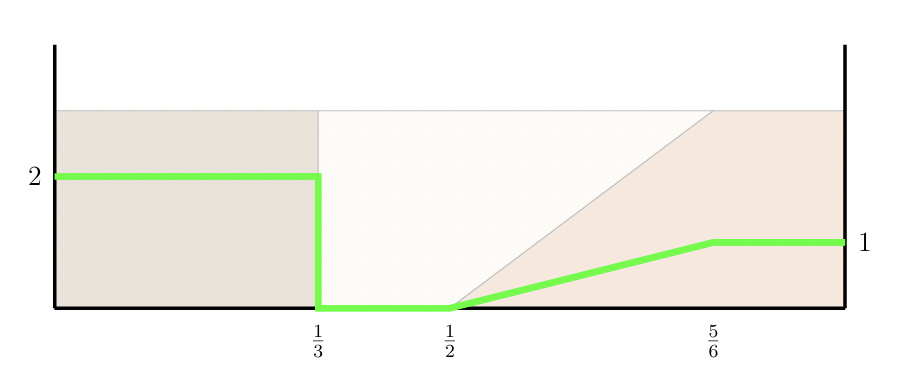
Figure 7 : L’aire sous la courbe donne la fonction d’évaluation \(V_C\) de Camille.

L’objectif est donc de trouver une répartition du gâteau \(G=(G_1, G_2,\ldots, G_n)\) où

• \(G_i\) est l’intervalle de gâteau alloué au joueur \(i\),
• \(G\) est une partition de \([0,1]\) : \(\forall i, j\in N\), on a \(G_i\cap G_j = \emptyset\) (un morceau de gâteau est attribué à au plus un joueur) et \(\cup_{i=1}^n G_i = [0,1]\) (tout le gâteau est réparti).

Le partage est dit proportionnel si chaque joueur considère qu’il a eu une part qui représente au moins \(\frac{1}{n}\) du gâteau, c’est-à-dire \(\forall i \in N, V_i(G_i) \geq \frac{1}{n}\). En reprenant la solution de la figure 4, on peut se rendre compte que \[V_B\left(0,\frac{1}{9}\right)=V_A\left(\frac{1}{9},\frac{4}{9}\right)=V_C\left(\frac{4}{9},1\right)=\frac{1}{3}.\] Ainsi chaque joueur considère que sa part vaut au moins un tiers du gâteau et cette solution est bien un partage proportionnel.

Un algorithme de partage

Pour deux joueurs, l’algorithme vu précédemment de « je partage, tu choisis » peut être décrit avec les notations comme suit :

• le premier joueur indique la valeur \(x\) telle que \(V_1(0,x)=V_1(x,1)=\frac{1}{2}\) ;
• si \(V_2(0,x)\geq V_2(x,1)\) le deuxième joueur prend la part \(G_2=[0,x]\) et le premier joueur prend l’autre part \(G_1=[x,1]\) ;
• sinon, le deuxième joueur prend la part \(G_2=[x,1]\) et le premier joueur prend l’autre part \(G_1=[0,x]\).

À partir de 3 joueurs, voici un algorithme de partage équitable utilisable en famille : une main pure et innocente positionne un couteau au point zéro et le déplace doucement sur le gâteau. Dès qu’un joueur considère que la part délimitée par le départ du couteau et son point courant vaut, pour son évaluation propre, la valeur de \(\frac{1}{n}\), il crie « stop » et il obtient alors cette part. Les joueurs restants répètent l’opération jusqu’à épuisement des joueurs et du gâteau.

Tant qu’il reste du gâteau, chaque joueur qui crie « stop » a obtenu une part qui de son point de vue vaut au moins \(\frac{1}{n}\). Avant qu’un joueur ne dise « stop », au plus \(n-1\) parts ont été prises par les autres joueurs et chacune de ces parts a, pour ce joueur, une valeur inférieure à \(\frac{1}{n}\). Comme le gâteau total vaut 1 pour tous les joueurs, tant qu’un joueur n’a pas dit « stop », le gâteau restant vaut, pour ce joueur, au moins \(1-\frac{n-1}{n}=\frac{1}{n}\). Au cours de l’algorithme, un joueur peut être tenté par la manipulation. En effet s’il ment et attend un peu après son évaluation à \(\frac{1}{n}\), il pourrait espérer avoir plus que cette part proportionnelle. Mais avec ce mensonge, il risque aussi d’obtenir moins à la fin. Et aussi le dernier joueur, qui peut être celui qui a trop attendu, peut même ne plus rien avoir du tout s’il a essayé de tricher !

Est-ce bien équitable ?

Jusqu’à présent, l’équité était garantie par le partage proportionnel. Mais une autre notion d’équité peut sembler plus pertinente : le partage sans envie où chaque joueur préfère sa part à la part des autres joueurs, ou plutôt où chaque joueur trouve que les parts des autres ne sont pas préférables à la sienne. Avec les notations, cela s’écrit \(\forall i,j \in N\), \(V_i(G_i) \geq V_i(G_j)\).

En effet, même si le partage de la figure 4 est proportionnel, les joueurs peuvent penser qu’il n’est pas équitable : Bob préfère la part d’Alice qui contient plus de chocolat noir, Alice celle de Camille qui est plus grande et Camille celle d’Alice qui contient du chocolat noir. Plus formellement, la part de Bob est \(G_B=\left[0,\frac{1}{9}\right]\), la part d’Alice est \(G_A=\left[\frac{1}{9}, \frac{4}{9}\right]\) et la part de Camille est \(G_C=\left[\frac{4}{9}, 1\right]\). Considérons le cas de Bob lorsqu’il compare sa part à celle d’Alice : \[V_B\left(0,\frac{1}{9}\right)=\frac{1}{3} < \frac{2}{3} = V_B\left(\frac{1}{9}, \frac{4}{9}\right)\] et donc, Bob préfère la part d’Alice à la sienne. De la même façon pour Alice: \[V_A\left(\frac{1}{9}, \frac{4}{9}\right)=\frac{1}{3} < \frac{5}{9} = V_A\left(\frac{4}{9}, 1\right)\] et Alice est envieuse de Camille. Vous pouvez vérifier que Camille est également mécontente : \[V_C\left(\frac{4}{9}, 1\right)=\frac{1}{3} < \frac{4}{9} = V_C\left(\frac{1}{9}, \frac{4}{9}\right).\] Le partage de la figure 8 ci-dessous, est noté \(G’_B=\left[0, \frac{1}{6}\right]\), \(G’_C=\left[\frac{1}{6},\frac{1}{3}\right]\) et \(G’_A=\left[\frac{1}{3},1 \right]\). C’est un exemple de partage sans envie pour Alice, Bob et Camille. En effet pour Alice \(V_A(G’_A)=\frac{2}{3} \geq V_A(G’_B)=V_A(G’_C)=\frac{1}{6}\). Pour Bob, on a \(V_B(G’_B)=V_B(G’_C)=\frac{1}{2}\geq V_B(G’_A)=0\). Et enfin, Camille considère que toutes les parts valent \(\frac{1}{3}\) donc sa part lui convient aussi bien que celle des autres.

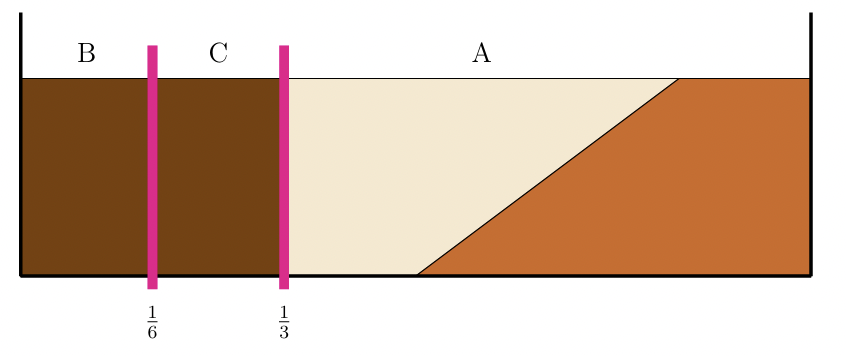
Figure 8 : Un exemple de partage sans envie du gâteau.

Dans l’algorithme du couteau qui se déplace décrit ci-dessus, menant à un partage proportionnel, les joueurs ne sont pas envieux de ceux qui ont choisi avant eux mais peuvent l’être de ceux qui choisissent après. On peut prouver que toute solution sans envie est proportionnelle mais que, comme le montre cet exemple, l’inverse n’est pas toujours vrai. Les méthodes pouvant amener à des partages sans envie sont plus complexes et demandent à chaque joueur de répondre à beaucoup plus de questions (voir l’algorithme constructif trouvé indépendamment par Selfridge et Conway en 1960 pour un partage sans envie à trois joueurs).

Si l’on veut garantir des solutions sans envie, on ne peut pas toujours se limiter à des parts de gâteau en un seul morceau, où chaque part est représentée par un seul intervalle. On modéliserait alors une part de gâteau comme une union d’intervalles de \([0,1]\).

En conclusion

Vous connaissez à présent deux façons de modéliser l’équité: le partage proportionnel et le partage sans envie. Les résultats proposés permettent de réfléchir à des algorithmes de partage de ressources et de comprendre comment prouver des propriétés d’équité.

On peut aussi comparer ces solutions à une version dite utilitariste (aussi appelée « de bien-être social »), c’est-à-dire une solution dont la somme des valeurs de toutes les parts des joueurs soit la plus grande possible. Une telle solution peut être globalement plus intéressante pour l’ensemble des joueurs. Dans ce cas, imposer des contraintes d’équité peut diminuer le bien-être global. Il s’agit donc de trouver un équilibre entre la satisfaction individuelle, l’envie mutuelle, la satisfaction collective, etc.

Pour reprendre plus formellement ces notions et voir comment elles s’intègrent dans un cadre plus large, vous pouvez consulter ce support de cours sur la répartition équitable de biens divisibles (niveau universitaire d’informatique ou de mathématiques appliquées). Pour aller plus loin, vous pouvez lire le chapitre 13 du Handbook of Computational Social Choice (2016) : Cake Cutting Algorithms de Ariel Procaccia (en anglais).