Comprendre la circulation océanique
Ces courants à grande échelle, parmi lesquels figure le célèbre Gulf Stream, jouent un rôle primordial dans la dynamique des océans, et bien entendu dans l’équilibre thermodynamique de notre planète. Il est donc essentiel de pouvoir les comprendre afin d’anticiper d’éventuels déséquilibres qui pourraient advenir, par exemple, dans le cadre du réchauffement climatique.
La modélisation mathématique et la simulation numérique constituent aujourd’hui des outils essentiels dans la démarche de compréhension de ces phénomènes complexes. La modélisation mathématique permet de représenter séparément les actions des différents mécanismes à l’origine des courants marins : la gravité terrestre, l’influence des courants atmosphériques (les vents), la force de Coriolis (due au mouvement de rotation de la Terre sur elle-même), l’attraction de la Lune… Il est alors possible d’envisager différents scénarii combinant ces mécanismes. Cela permet d’identifier les mécanismes principaux expliquant tel ou tel phénomène observé ou de réaliser des projections dans l’avenir via les simulations numériques.
C’est un processus élémentaire qui est à l’origine de la mise en mouvement de gigantesques masses d’eau. En effet, c’est sur la différence de masse volumique entre ces dernières que repose ce phénomène de convection. Cela s’explique par des formules mathématiques, et peut être illustré grâce à des simulations réalisées par ordinateur, mais aussi avec une expérience réalisable par tous, à l’aide de bouteilles plastiques, de pailles et de sirops alimentaires.
Une expérience à la portée de tous
Rappelons au préalable que la masse volumique d’un liquide est en relation avec sa température. On observe en effet expérimentalement que la masse volumique évolue comme une fonction décroissante de la température. Lorsque l’on chauffe une quantité d’eau donnée, le volume qu’elle occupe augmente (l’eau se dilate !) ; sa masse restant inchangée, nous pouvons en conclure que sa masse volumique diminue.
Afin de mettre en évidence le phénomène de convection que nous voulons étudier, nous avons réalisé une expérience filmée. Cette expérience utilise deux bouteilles en plastique qui ont été préalablement percées chacune de deux trous, à deux hauteurs distinctes H1 et H2, identiques pour les deux bouteilles, puis reliées l’une à l’autre grâce à deux pailles en position horizontale. L’étanchéité du système est garantie par l’utilisation de mastic à chaque insertion des pailles dans les bouteilles. Les deux pailles ainsi disposées aux hauteurs H1 et H2 permettent donc des échanges entre les bouteilles, selon le principe des vases communicants.
Avant de débuter l’expérience, les pailles sont pincées en leur milieu pour éviter les échanges. On remplit alors chacune des deux bouteilles d’eau colorée (par un sirop alimentaire). La quantité de sirop dans chacun des liquides est bien entendu strictement identique afin de ne pas fausser l’expérience.
Dans un premier temps, la température des deux liquides est identique. Leur masse volumique est alors également identique. Il est donc naturel que, lorsque les pinces sont retirées, il ne se passe rien ! Les fluides sont en équilibre…
En revanche, si l’on reproduit l’expérience en chauffant préalablement l’un des deux liquides (ici le rouge), on observe un mouvement, provoqué par la différence de masse volumique entre les deux bouteilles. L’eau rouge, parce qu’elle est plus chaude et donc moins dense, passe dans la paille supérieure, tandis que l’eau verte, qui est plus dense, passe dans la paille inférieure. Si on laisse le système agir sans intervention extérieure, on observe un équilibre final dans lequel les deux bouteilles sont remplies de façon identique : eau chaude en haut, eau froide en bas, et bien sûr une zone de mélange entre les deux.
Bouteilles et océanographie.
Visionner la vidéo réalisée par Pierre-Olivier Gaumin – Durée : 04 min 55 s.
Cette expérience simple permet d’illustrer un processus qui est à l’origine de l’existence de courants marins à grande échelle, et nous allons tenter maintenant de comprendre pourquoi et comment.
Modélisation et simulation numérique
Les équations qui régissent l’évolution d’un fluide en mouvement résultent directement de l’application des lois et principes généraux de la mécanique et de la thermodynamique. Le premier, très simple, exprime la conservation de la masse du fluide. Considérons à un instant donné un ensemble de particules d’un fluide ; au cours du mouvement, cet ensemble va changer de position, de forme et de dimension mais restera constitué des mêmes particules ; ainsi la masse du fluide présent dans cet ensemble se conserve à tout instant.
En termes mathématiques, ce principe de conservation s’exprime à l’aide d’une équation reliant la masse volumique du fluide ρ et sa vitesse dans l’espace, le vecteur u = (ux, uy, uz) :
δt ρ div (ρu) = 0.
Cette équation (ou plutôt, pour être exact, sa version intégrale) peut se comprendre de la manière suivante : la variation (dans le temps) δt ρ de la masse du fluide contenue dans un domaine donné est égale au bilan des flux de masse ρu . n traversant les frontières du domaine (entrée et sortie de fluide). Le vecteur n désigne la normale à la frontière du domaine considéré. Le lien entre l’opérateur divergence (div) et les flux normaux se fait via la formule de Green-Ostrogradski.
Le second principe est celui de conservation de la quantité de mouvement ρu. Ce n’est rien d’autre que le principe fondamental de la dynamique de Newton : l’accélération d’un corps en mouvement est proportionnelle à la somme des forces auxquelles il est soumis.
En termes mathématiques, si nous supposons que la seule force extérieure s’appliquant sur le fluide est la gravité définie par le vecteur g = (0, 0, –g), ce principe se traduit par l’équation vectorielle suivante :
δt (ρu) div (ρu ⊗ u) div (τ̄(u)) grad(p) = ρg.
À l’instar de ce que nous avons expliqué pour l’équation de conservation de la masse, le premier terme δt (ρu) exprime la variation temporelle de la quantité de mouvement dans un domaine donné, le second terme représentant le bilan des flux de quantité de mouvement (ρu ⊗ u) . n aux frontières de ce domaine. Les autres termes, conformément à la loi de Newton, représentent les forces s’exerçant sur le fluide.
Plus précisément, le terme div (τ̄(u)) exprime la présence d’une force intrinsèque au fluide : la viscosité. Celle-ci désigne la résistance que tout fluide oppose à sa mise en mouvement. Le terme grad(p) représente la force exercée par les différences de pression (le gradient de pression).
Il est important de remarquer que l’égalité précédente constitue un système de trois équations : une pour chacune des trois composantes (ux, uy, uz) de la vitesse. D’autre part, avec sa forme particulière g = (0, 0, –g), la gravité n’influence que la composante verticale uz de la vitesse.
Le système composé des deux équations vectorielles ci-dessus n’est pas fermé, ceci signifie qu’il ne contient pas assez d’informations pour déterminer la vitesse du fluide u et sa masse volumique ρ. Il est nécessaire de lui ajouter ce que l’on appelle une loi d’état, par exemple une équation définissant la masse volumique du fluide. Les lois d’état sont des lois établies dans des cas idéaux (avec un fluide parfait) ou simplement des lois empiriques obtenues de façon expérimentale. Elles dépendent alors du fluide considéré.
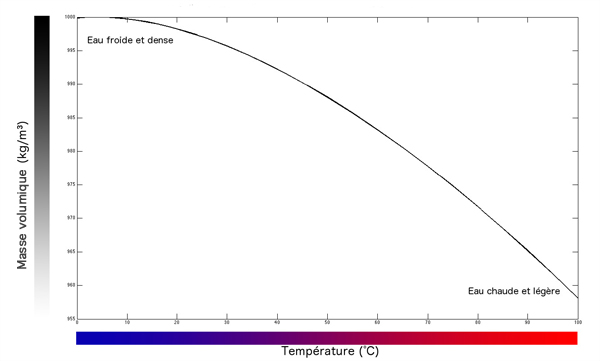
Variation de masse volumique de l’eau douce en fonction de la température.
Dans l’application qui nous intéresse, nous pouvons choisir de définir la masse volumique comme une fonction décroissante de la température T. Ce choix décrit bien la réalité physique que nous observons expérimentalement. La figure ci-dessus donne le profil de variation de la masse volumique de l’eau en fonction de la température, obtenu expérimentalement. Pour simplifier les modèles, il est parfois utile de choisir une loi de la forme :
ρ = a – bT
où a et b sont des coefficients positifs.
Il reste maintenant à déterminer l’évolution de la température, ce que nous faisons à l’aide d’une équation (dite de transport-diffusion), qui représente la convection et la conduction de la chaleur dans le fluide. Cette équation traduit la conservation de l’énergie du fluide :
δt(ρT) div (ρTu) – div (λ grad(T)) = 0.
Dans cette équation, le paramètre λ représente la conductivité thermique du milieu liquide. Elle est constituée de termes de convection ρTu et de conduction λ grad(T) (loi de Fourier).
Les équations que nous venons de décrire sont connues sous le nom d’équations de Navier-Stokes. Elles ont été établies au XIXe siècle mais constituent encore aujourd’hui un des plus grands défis pour les mathématiciens, puisque nous ne disposons pas encore de principe général d’existence et d’unicité de solutions régulières de ces équations. Ce problème fait partie de la liste des septs problèmes proposés en 2000 par le Clay Mathematical Institute, une fondation américaine privée, et sa résolution sera récompensée d’un prix d’un million de dollars.
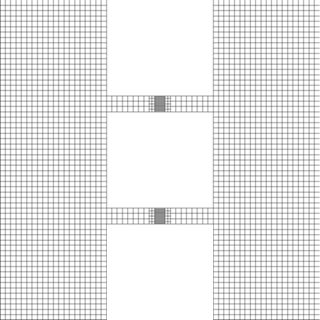
Exemple de maillage du domaine de calcul.
Nous ne connaissons pas les solutions de ces équations, mais nous pouvons néanmoins nous appuyer sur des simulations numériques par ordinateur pour nous en approcher au plus près. Le principe général d’une simulation numérique est de découper en « petits » éléments le domaine sur lequel nous voulons approcher la solution, on parle de maillage du domaine de calcul. La figure ci-contre montre un exemple de maillage (2D) que nous utilisons pour simuler l’expérience présentée plus haut. Sur chacun des « petits » sous-domaines, nous supposons que la solution a une forme très simple (par exemple, qu’elle est constante ou linéaire), le point crucial étant qu’elle puisse être représentée par un nombre fini de coefficients. Nous déduisons alors des équations de Navier-Stokes un problème dit discret reliant tous ces coefficients. L’écriture de ce problème discret n’est pas toujours simple et nécessite quelquefois des techniques mathématiques d’analyse numérique évoluées.
Il est ensuite possible de résoudre ce problème grâce à un algorithme, que l’on traduit dans un langage de programmation afin d’être exécuté sur un ordinateur.
La vidéo ci-dessus montre le résultat d’une simulation numérique reproduisant l’expérience présentée plus haut. Il s’agit d’une approximation numérique des solutions du système de Navier-Stokes présenté plus haut, où l’équation d’évolution de la température a été remplacée par l’équation de Cahn-Hilliard que nous ne décrirons pas en détail ici. Le principe général de ce modèle numérique est d’utiliser une représentation « épaisse » des interfaces (il s’agit de la zone en vert sur la vidéo) et d’en décrire l’évolution tout en garantissant que son épaisseur va rester constante au cours du temps. Nous constatons que le comportement de la solution obtenue par simulation numérique est bien identique à celui observé dans l’expérience. Ceci met en particulier en avant le rôle moteur de la gravité (seule force extérieure considérée dans notre modèle !) associé à la différence de masse volumique (conséquence de la différence de température) entre les deux masses d’eau.
Nous n’avons pas reproduit la simulation dans le cas où les températures initiales des bouteilles sont identiques, car il ne se passe rien. En effet, comme nous l’avons mentionné précédemment, le système est déjà à l’équilibre. Ceci se traduit mathématiquement par le fait que le système d’équations admet pour solution particulière (T = constante, ρ = constante, u = 0, p = -ρgz).
Vers des modèles océaniques réalistes
Bien entendu, dans les océans du globe, les phénomènes sont plus complexes que dans les deux bouteilles de l’expérience présentée ci-dessus. Historiquement cependant, le rôle essentiel de la masse volumique de l’eau comme moteur principal de la circulation océanique à grande échelle a bel et bien été mis en évidence dans des bacs de laboratoire (par un océanographe suédois, J. W. Sandström, en 1908).
La masse volumique des eaux des océans varie pour deux raisons essentielles :
- la température, comme dans nos bouteilles, a une influence négative sur la masse volumique : plus la température augmente, plus la masse volumique diminue.
- la salinité joue également un rôle important, il est cette fois positif : plus l’eau de mer est chargée en sel, plus elle est dense. On peut s’en convaincre en prenant un litre d’eau dans une casserole, et en y ajoutant du sel. Le volume ne change pas, il reste d’un litre, mais par contre la masse de l’eau salée est la somme de celle de l’eau et du sel ajouté (on peut dissoudre plus de 300 grammes de sel par litre à 25C !), et, par conséquent, la masse volumique augmente au fur et à mesure que l’on ajoute du sel.
Ainsi, dans l’océan, on peut exprimer la masse volumique de l’eau en fonction de la température T et de la salinité S à l’aide d’une équation de la forme suivante (un petit peu simplifiée) :
ρ(T, S) = -αT βS.
On constate alors dans l’océan le même phénomène que dans nos deux bouteilles : certaines masses d’eau sont plus denses que d’autres, et les différences de masse volumique contribuent à la mise en mouvement de ces masses d’eau.
Dans les océans Arctique et Atlantique Nord, l’eau de mer est froide et très salée. Ceci s’explique par l’intensité du vent qui produit à la fois un intense refroidissement et une augmentation de la salinité des eaux (du fait de l’évaporation des molécules d’eau), mais également par le fait que, dans les régions polaires, une partie de l’eau de mer se transforme en glace, rejetant le sel qu’elle contient dans l’eau environnante. L’eau de mer dans ces régions-là est donc très dense en comparaison aux eaux des régions tropicales plus chaudes et moins salées. Ceci, comme dans nos bouteilles, amorce la plongée des eaux de l’océan Arctique et Atlantique Nord vers les fonds marins, et constitue une véritable pompe pour la circulation à grande échelle.
Ces eaux profondes traversent l’océan Atlantique du nord au sud et sont entrainées vers les océans Indien et Pacifique où elles se réchauffent et font peu à peu surface. Elles reviennent ensuite du sud vers le nord de l’océan Atlantique sous forme de courant de surface (dont le mouvement est également influencé par les vents, la rotation de la Terre, etc). Cette circulation à grande échelle forme une sorte de tapis roulant à l’échelle du globe. On l’appelle la circulation thermohaline (« thermo » pour la température et « haline » pour la salinité).
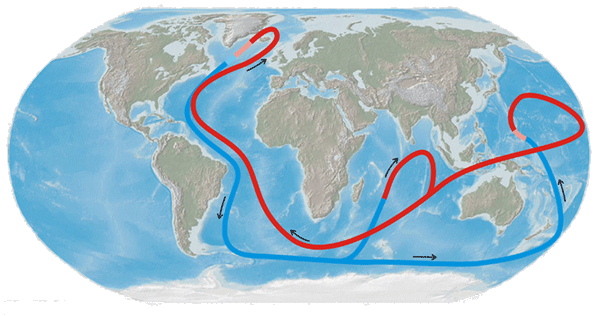
Le tapis roulant de la circulation thermohaline. En bleu, les courants profonds ; en rouge, les courants de surface.
Source : Reflexions, le site de vulgarisation scientifique de l’université de Liège.
Parmi les effets possibles du réchauffement climatique, figurent deux éléments dont l’impact pourrait être désastreux sur la circulation thermohaline : l’augmentation de la pluviométrie aux latitudes moyennes et élevées, ainsi que la fonte de la glace de mer (constituée d’eau douce) aux pôles. Ces deux phénomènes apportent de l’eau douce en surface et ont donc tendance à diminuer la salinité de l’eau, s’opposant ainsi, dans les zones habituelles de plongée des eaux denses (Mer du Labrador, Mer de Norvège), à la circulation thermohaline naturelle.
Comme expliqué précédemment, les équations qui décrivent la circulation thermohaline sont des équations de bilan : conservation de la masse, conservation de l’énergie, conservation de la quantité de mouvement. La masse volumique y intervient en particulier dans l’équation de la conservation du mouvement vertical, via le terme de force de gravité. On retrouve ainsi son rôle sur la plongée des eaux denses et la remontée des eaux peu denses. L’équation de transport-diffusion de la température et son analogue pour la salinité expliquent quant à elles le transport des masses d’eau le long des courants.
La vidéo suivante montre le résultat d’une simulation numérique représentant la trajectoire d’un objet dans l’océan mondial (une bouteille à la mer par exemple, mais ouverte, afin qu’elle se remplisse d’eau et puisse plonger en profondeur en suivant les courants).
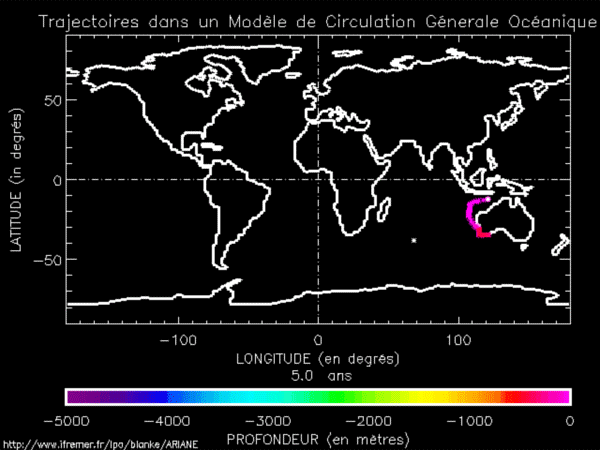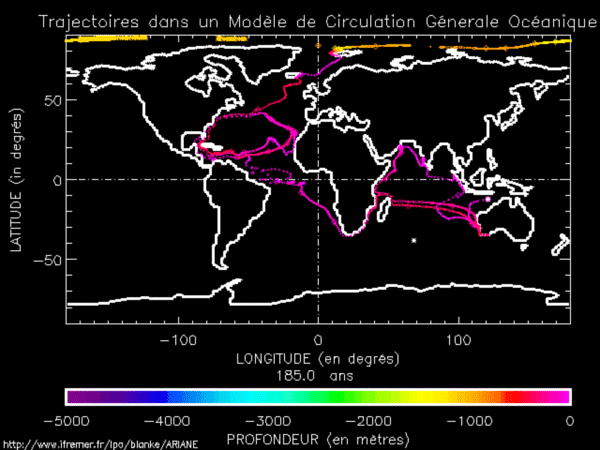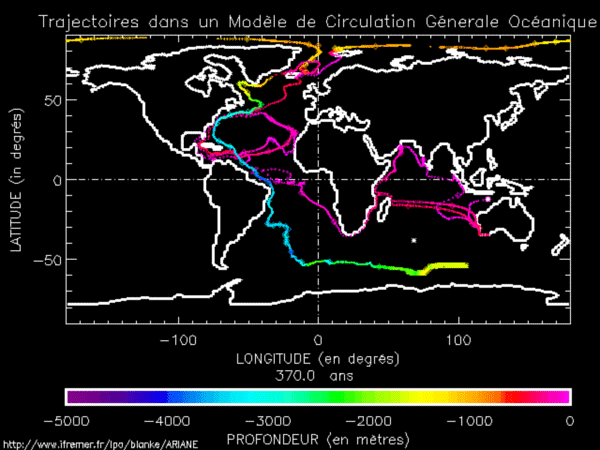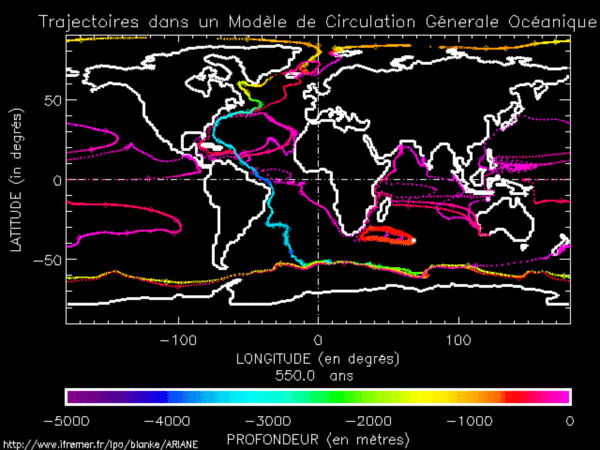
Trajectoire d’une particule d’eau dans l’océan mondial. Animation réalisée par Bruno Blanke, CNRS Laboratoire de Physique des Océans, UMR 6523, CNRS-Ifremer-IRD-UBO, Brest, France.
Au début de son périple, la bouteille se trouve à l’ouest de l’Australie, en surface de l’océan. Au fur et à mesure que le temps passe, elle se déplace tout autour du globe en suivant les courants marins, elle fait plusieurs tours dans le Gulf Stream, avant de remonter vers le nord et d’amorcer sa plongée (remarquer la couleur qui change avec la profondeur). Elle parcourt ensuite tout l’Atlantique du nord au sud en profondeur, avant de remonter en surface. À la fin de la simulation, qui a duré 550 ans, la bouteille à la mer a fait plusieurs fois le tour du globe ! La trajectoire exacte de la bouteille ne peut s’expliquer qu’en considérant de nombreux processus comme la force de Coriolis, les vents de surface, les courants côtiers, etc. Néanmoins, la circulation thermohaline que nous venons d’évoquer permet de justifier son parcours à grande échelle.
À la recherche de ressources dans le cadre du sujet TIPE 2019-2020 ?
Consulter un texte pour « débroussailler » le sujet sur Pixees.fr, un site de ressources autour des sciences du numérique.
+ Lire l'articleNewsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Maëlle Nodet
Enseignant-chercheur à l'Université Grenoble Alpes, membre du laboratoire de mathématiques appliquées Jean Kuntzmann et de l’équipe AIRSEA d’Inria Grenoble Rhône-Alpes.

