Comprendre un processus cognitif grâce à l’analyse statistique du mouvement des yeux

Dans cet article, nous proposons une introduction à la statistique en tant que science qui vise à analyser des données afin d’identifier des caractéristiques sous-jacentes aux processus qui les ont produites. Pour illustrer notre propos, nous nous appuyons sur l’exemple de l’analyse conjointe du mouvement des yeux et d’électroencéphalogrammes (EEG) enregistrés lors d’expériences de lecture, afin d’en déduire différentes phases cognitives. Ces phases sont mises en évidence par un modèle d’analyse de séquences de mouvements oculaires. Une fois les phases identifiées, les données d’EEG permettent de caractériser les connexions cérébrales spécifiques à chaque phase.

Décrypter des processus latents grâce à la statistique

Dans la langue de tous les jours, on assimile souvent « les statistiques » à la simple collecte de données. En réalité, la statistique — terme utilisé au singulier pour désigner la discipline et au pluriel pour désigner les données ou leurs résumés — est une discipline qui vise à utiliser ces données, soit pour prédire des valeurs futures et leur incertitude, soit pour inférer des connaissances quant aux phénomènes qui les ont produites. Ces problèmes d’inférence sont par nature très variés et dépendent du contexte applicatif. Certains problèmes sont résolus très simplement (par exemple estimer la probabilité de succès d’une personne candidate à une élection, abstraction faite des erreurs de restitution par les médias) tandis que d’autres le sont de manière plus complexe (par exemple, identifier comment la progression sémantique d’un texte détermine ou non l’activation de certaines connexions cérébrales).

On peut résumer ainsi : il s’agit, grâce à l’analyse de données, de trouver des caractéristiques cachées d’intérêt dans des processus qui produisent ces données.

L’oculométrie révélatrice de processus cognitifs

La statistique trouve naturellement sa place dans les neurosciences : en effet, quoi de plus cachés que la conscience, la connaissance et les processus cognitifs mis en œuvre quand nous réfléchissons ou que nous exécutons une tâche de la vie quotidienne avec facilité, comme la conséquence de notre apprentissage au cours de notre développement. Prenons par exemple une activité habituelle où nous sommes devant un écran montrant une page d’un site web d’un journal en ligne. Nous sommes capables d’apporter de subtiles variations à un processus complexe comme la lecture suivant notre intérêt du moment : un texte pourra être négligé après avoir lu quelques mots, ou bien lu « en diagonale », ou bien encore de façon très attentive. Ce type d’expérience de lecture a pu être caractérisé quantitativement en laboratoire, afin d’étudier à la fois les mouvements des yeux (on parle d’enregistrements oculométriques, qui produisent des séquences de données appelées traces oculométriques) mais aussi les signaux électroencéphalographiques. Le but est de décrypter ces processus dans une tâche de lecture (voir la référence Frey et collab., 2013).

Figure 1. Un exemple de trace oculométrique.
La séquence observée est une succession de fixations (arrêt du regard sur un mot avec acquisition d’information visuelle, représenté ici par un cercle de rayon proportionnel à la durée de la fixation) et de saccades (mouvement bref d’une position à l’autre du texte pendant lequel la lecture n’est pas possible, représenté ici par un segment). Le texte est présenté aux participants avec un thème qui suivant les cas, peut être lié au texte (par exemple ici, « Dégradation de l’environnement ») ou non (par exemple « La conquête spatiale »). On associe la fixation à un ou plusieurs mots (affichés en noir au-dessus des fixations) contenus dans une fenêtre représentant le fait que le champ visuel ne se réduit pas à un point, mais à une région (empan perceptif) à l’intérieur de laquelle de l’information utile peut être extraite. Certains mots-outils peu informatifs sont ignorés dans cette étape d’association.

L’expérience s’apparente à une revue de presse : nous présentons un texte et un thème à un participant qui doit déterminer le plus rapidement possible s’il y a ou non concordance entre le texte et le thème. Pendant la durée de la tâche, les mouvements des yeux et un électroencéphalogramme sont enregistrés (voir la figure 1 ci-dessus). Les EEG mesurent l’activité électrique de différentes zones du cerveau à l’aide d’un jeu d’électrodes disposées régulièrement sur le cuir chevelu (plus bas, voir la figure 5b), ce qui permet de savoir quelles sont les zones activées à différents moments. La difficulté d’analyser directement les EEG est liée tout d’abord à leur aspect très bruité et à leur multidimensionnalité (une dimension pour chacune des 32 électrodes). À ceci s’ajoutent de multiples sources de variabilité expérimentales et cognitives : d’une personne à l’autre (positionnement des électrodes), d’une expérience de lecture à l’autre pour un sujet donné, voire au sein d’une même expérience de lecture – nous allons mettre en évidence ci-après que le processus de lecture n’est pas homogène.

L’objectif de cette expérimentation se démarque de celui des interfaces cerveau-machine, qui visent à fournir un outil qui permette d’interagir avec un ordinateur — soit pour qu’il prononce des mots lus, ou qu’il déplace des objets. Notre but ici est plutôt de comprendre et caractériser de manière quantitative le fonctionnement du cerveau lors de différentes étapes de réflexion de lectrices sur le point de prendre une décision. Il est très difficile de lire directement dans ces EEG une stratégie mise en œuvre pour mener à bien la tâche, du fait de leur caractère bruité (voir la figure 2 ci-dessous) et de la multiplicité des sources de variabilité.

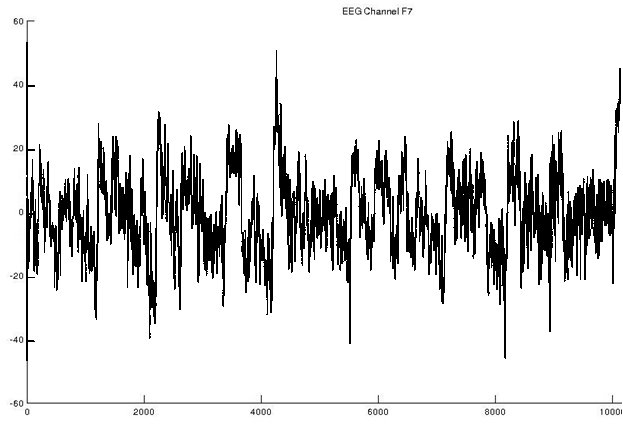
Figure 2. Exemple d’électroencéphalogramme (EEG) associé à une expérience de lecture.
Les EEG sont enregistrés simultanément par 32 électrodes, représentées schématiquement sur la figure 5b) : ici on n’a représenté que l’enregistrement associé à l’électrode F7.

Les mouvements des yeux ont des caractéristiques statistiques un peu plus universellement partagées que les EEG dans notre population de participantes. Ils sont mesurés ici grâce à des caméras infrarouges, placées en face de la personne et reliées à un ordinateur qui enregistre le parcours visuel. Nous faisons l’hypothèse qu’un changement de dynamique dans le mouvement des yeux reflète un changement d’étape dans la lecture du texte et dans le parcours qui mène à la décision, conduisant à un certain nombre de phases de lecture avec des propriétés statistiques contrastées d’une phase à l’autre. Ces phases sont a priori inconnues mais on peut imaginer qu’il puisse exister par exemple des phases de lecture normale, lecture en diagonale, de recherche d’information, de confirmation ou de décision. Les propriétés statistiques sont résumées à travers la loi de probabilité de cinq types de mouvements des yeux reflétant la dynamique de lecture : revenir en arrière de deux mots ou plus (régression longue, LReg), d’un seul mot (régression, Reg), refixer le même mot (Ref), fixer le mot suivant (progression, Pr) ou sauter des mots dans le sens de lecture (progression longue, LPr) – voir la figure 3 ci-dessous. Ces types constituent des descripteurs qui ont été choisis parmi d’autres pour leur invariance par rapport à la mise en page, leur facilité d’interprétation et leur adéquation au traitement statistique ci-après. On peut alors construire un modèle qui vise à reproduire les principaux traits du processus de lecture :
a) ces phases existent et ont des durées aléatoires et spécifiques à chaque phase ;
b) la probabilité de la phase suivante dépend de la phase courante ;
c) d’une phase à l’autre, les probabilités des cinq types de mouvements des yeux sont différentes.

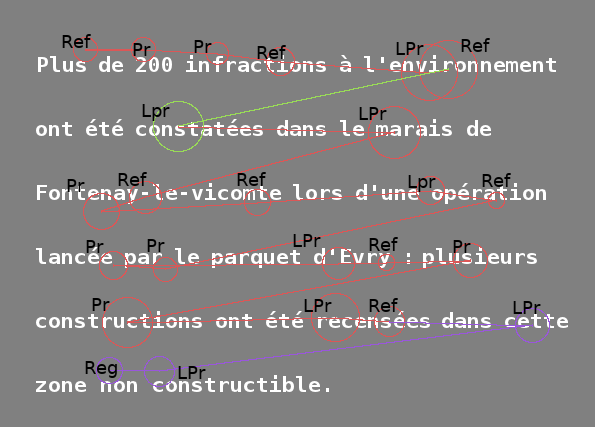
Figure 3. Segmentation de la trace oculométrique de la figure 1 à l’aide d’un modèle statistique.
La succession de fixations est transformée en succession de types de mouvement des yeux : revenir en arrière de deux mots ou plus (type absent de cette séquence), d’un seul mot (régression, Reg), refixer le même mot (Ref), fixer le mot suivant (progression, Pr) ou sauter des mots dans le sens de lecture (progression longue, LPr). La segmentation représentée ici fait intervenir un état rouge de lecture normale, vert de recherche d’information et violet de lecture lente pour confirmation de la pré-décision.

Grâce à l’acquisition de données oculométriques résumées à des séquences composées de ces cinq types, le modèle « apprend » ces différentes probabilités, au sens où il les estime en maximisant une mesure de concordance entre ces probabilités (qui relèvent de concepts liés au modèle) et les données (qui relèvent de l’expérimentation). Puis étant donné une expérience de lecture particulière, il est capable de prédire quelles en ont été les phases (c’est-à-dire de découper la trace oculométrique en tronçons statistiquement homogènes appelés segments, chacun d’entre eux étant associé à une phase). Il s’agit d’une étape, dite de segmentation, illustrée par la figure 3 ci-dessus, où le code de couleur correspond aux différentes phases : en rouge la lecture normale, en vert la recherche d’information complémentaire et en violet la lecture lente de confirmation / décision. Il existe également une phase de lecture rapide « en diagonale » en bleu, qui n’a pas été utilisée par la participante dans la lecture du texte présenté ici. Peut-être l’a-t-elle utilisée dans un autre texte, ou ne l’utilise-t-elle jamais : dans ce dernier cas, ce sont d’autres participants qui auront permis de mettre en évidence l’existence de cette phase. L’étape d’apprentissage du modèle statistique ne nous fournit que des estimations des différentes probabilités de types de mouvements d’yeux par phase. Il nous reste à définir des interprétations et dénominations de ces phases grâce à ces probabilités. Ainsi, la phase de lecture rapide a une probabilité de LPr plus élevée que dans les autres phases, celle de confirmation / décision, une probabilité de LReg et Reg plus élevée, etc. On peut alors revenir à nos EEG qui se trouvent eux-mêmes segmentés en tronçons via les phases de lecture déduites des mouvements des yeux (figure 3).

Cette opération de segmentation a pour effet non seulement de rendre les EEG plus homogènes statistiquement, mais aussi de les recaler puisqu’en entrant dans une phase donnée, les participants en sont à des étapes similaires de l’analyse du texte… du point de vue de la stratégie de lecture. N’oublions pas cependant que celle-ci est censée refléter leur degré de maturité vis-à-vis de la prise de décision : on obtient donc un aperçu synthétique des processus cognitifs mis en œuvre, révélés indirectement au travers du mouvement des yeux.

On analyse ensuite les EEG par segment, afin de s’assurer qu’ils ont une signature, c’est-à-dire des propriétés statistiques, différentes d’une phase à l’autre.

Plutôt que de chercher à associer une signature à chaque zone cérébrale, il apparaît plus discriminant (relativement aux phases) d’associer une signature entre paires de zones, correspondant à la corrélation entre les valeurs mesurées dans ces zones. Ceci est un moyen de quantifier la connectivité cérébrale fonctionnelle qui caractérise les interactions entre paires de régions cérébrales. La mesure de cette connectivité est complexe et nécessite des méthodes à l’interface entre statistique et traitement du signal, voir la figure 4 ci-dessous.

Figure 4. Illustration de la méthode pour extraire les graphes de connectivité cérébrale.
Dans notre cas, la méthode d’observation du fonctionnement cérébral (protocole d’acquisition) est l’EEG. Chaque capteur représente le signal pour une région du cerveau. La connectivité est extraite à partir des séries temporelles avec des méthodes statistiques comme la corrélation. Puis les graphes de connectivité sont construits en ne conservant que les valeurs les plus fortes de connectivité.

Le résultat de chacune de ces méthodes sera un ensemble de valeurs pour les paires de régions qui finaliseront la construction de graphes de connectivité. Cette étape est détaillée dans la section suivante. Notons que nous utilisons ici les traces oculométriques à la fois pour mettre en évidence des stratégies de lectures et faciliter leur mise en relation avec les EEG, mais l’analyse des traces oculométriques seules pourrait par exemple permettre, dans d’autres contextes de recherche, de comparer la facilité de lecture induite par différentes mises en page d’un document.

Inférence de la connectivité cérébrale fonctionnelle par phase

Le problème de l’étude de la connectivité cérébrale fonctionnelle au travers de l’analyse conjointe du mouvement des yeux et d’EEG est emblématique de l’utilisation de modèles statistiques. Il reflète en effet les enjeux présentés en introduction : dépendances spatiales et temporelles, processus latents impactant les observations, hétérogénéité des séquences d’observations due notamment à la variabilité d’un individu à l’autre, mais aussi la variabilité induite par l’utilisation de différentes stratégies par un même individu.

La notion de connectivité cérébrale permet de modéliser le fonctionnement du cerveau sous la forme d’un réseau de connexions : une vision connectiviste plutôt qu’une vision phrénologique. En effet dans ce dernier cas, chaque région cérébrale est attachée à une fonction indépendamment des autres. La vision connectiviste est apparue dans les années 2000, et depuis elle domine les études actuelles sur le fonctionnement du cerveau dans les pathologies et sur les études d’apprentissage. Dans cette approche connectiviste, chaque région du cerveau est représentée par un nœud du réseau et les connexions entre régions sont représentées par les liens entre nœuds. Le réseau du « mode par défaut », présent dans les moments de repos de la personne, a ainsi été mis en évidence pour caractériser un réseau de veille qui joue un rôle particulier dans les processus d’activation lors de la réalisation d’une tâche. Au cours de celle-ci, ce réseau de veille laisse la place à des réseaux spécifiques à différents types d’activations (par exemple des réseaux sensoriel, moteur, visuel…). En suivant la même idée, la segmentation des traces oculométriques en phases de lecture permet de mettre en évidence le réseau spécifique à chacune de ces phases, ce qui permet de confirmer leur interprétation en tant qu’étapes cognitives dans la résolution du problème posé.

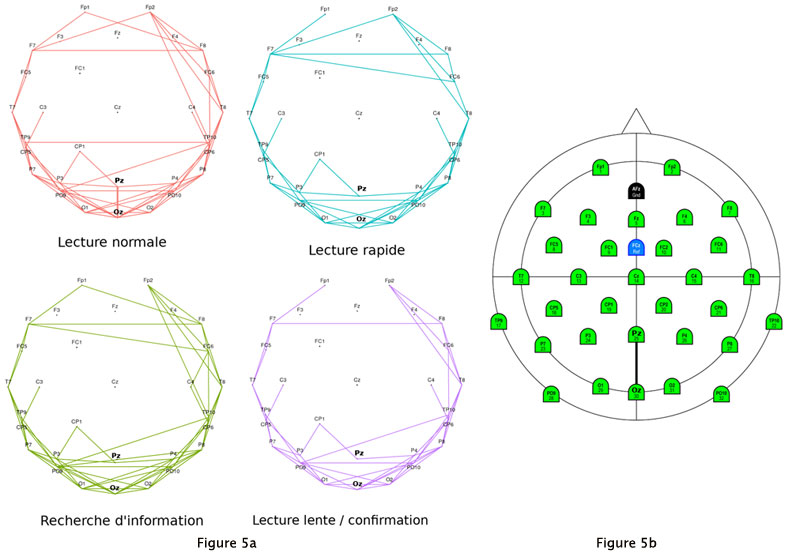
Figure 5. Activation différentielle des connexions cérébrales suivant la stratégie de lecture.
a) La connectivité cérébrale pour chacune des stratégies est illustrée par un graphe. La comparaison entre ces derniers permet d’illustrer quelles connexions sont spécifiques aux stratégies (par exemple Pz ↔Oz en lecture normale). La position des électrodes est représentée sur la figure de droite.
b) Le triangle en haut de la figure représente le nez de la personne et le disque de plus grand diamètre représente la tête vue de dessus. Les électrodes Pz (pariétale médiane, un peu derrière la zone centrale et au milieu de l’axe latéral) et Oz (occipitale médiane, à l’arrière de la tête) sont indiquées en caractères gras. Sur les quatre graphes de la partie a), le nez et les cercles n’apparaissent pas mais les électrodes sont représentées avec les mêmes positions que sur la partie b).

On peut ainsi voir sur la figure 5 ci-dessus que la mise en œuvre des différentes stratégies de lecture abordées en amont fait intervenir des ensembles de connexions, c’est-à-dire un réseau, spécifiques à chaque stratégie.

Ces réseaux correspondent à la notion mathématique de graphe. L’identification d’un graphe de corrélations à partir de valeurs observées sur les différents nœuds se résout par des méthodes statistiques complexes. Il est plus accessible d’aborder la génération de données aléatoires sur un graphe connu. Cette opération est réalisée par le programme ci-dessous. Dans le contexte présenté précédemment, il faut s’imaginer une donnée comme la valeur du signal EEG à un instant fixé. Chaque région cérébrale est représentée par un nœud du graphe et chaque connexion est représentée par une arête du graphe. Les valeurs simulées doivent l’être en respectant les dépendances induites par les connexions entre régions. La simulation est basée sur une loi de probabilité relative à ces valeurs, telle que la valeur d’un nœud est une moyenne des valeurs des nœuds voisins, plus un bruit. En réalité la problématique abordée ci-dessus en neurosciences relève plutôt d’un problème inverse : à partir de la valeur observée en chaque nœud, l’analyse statistique vise à retrouver le graphe des connexions. Une autre manière de voir le problème direct est de l’assimiler à un programme aléatoire qui part d’un graphe connu pour générer des données et le problème inverse, comme un programme (que vous pouvez tester en suivant le lien) qui part de données et vise à retrouver le graphe sous-jacent au problème direct. 

La connectivité cérébrale est aussi impliquée dans différentes pathologies (maladie d’Alzheimer, troubles du spectre autistique…) : dans certaines, en tant qu’indicatrice de l’apparition de la maladie et dans d’autres, comme facteur de dysfonctionnement du cerveau… ce qui nous ramène une fois de plus à des méthodes statistiques pour développer des méthodes de dépistage dotées d’une précision satisfaisante !

Les auteurs remercient Anne Guérin-Dugué (Gipsa-Lab, Grenoble) pour ses commentaires et conseils visant à améliorer cet article, ainsi que les différents relecteurs et l’équipe éditoriale d’Interstices.