
Compter les triangles
Présentation du jeu
On s’intéresse ici à un casse-tête classique (dont quelques variantes simplifiées ont souvent été utilisées dans des concours de Mathématiques en collège, comme Kangourou).
On considère une suite de triangles équilatéraux (c’est-à-dire dont la longueur des trois côtés est égale). Le triangle de base est celui dont les côtés sont égaux à 1. La suite est construite en ajoutant une ligne de petits triangles à la base du précédent, comme c’est illustré dans la figure 1. Le jeu consiste à énumérer tous les triangles équilatéraux, quelle que soit leur longueur, contenus dans le k-ième terme de cette suite. L’objectif visé est de déterminer combien l’élément k possède de triangles équilatéraux pour n’importe quelle valeur de k. On note ce nombre \(N_k\).

Figure 1 : Les 4 premiers termes de la suite des figures triangulaires, de gauche à droite. Chacun est construit en ajoutant une ligne de petits triangles à la base du précédent.
Les premiers éléments de cette suite :
- Bien sûr, le premier terme (celui que nous avons appelé le triangle de base) contient un seul triangle : \(N_1=1\)
- On a deux types de triangles dans le second terme de la suite : un grand triangle dont les côtés sont de longueur 2 et 4 triangles de base, donc \(N_2=1+4=5\).
- De même, on a 3 types de triangles dans le troisième terme : un grand de côté 3, 3 triangles moyens de côté 2 et 9 triangles de base, soit \(N_3=1+3+9=13\).
Quel est le nombre de triangles contenus dans le quatrième terme de cette suite ?
Pour le trouver, on procède à l’énumération comme nous l’avons fait pour les premiers termes de la suite en comptant tous les triangles, du niveau le plus grossier (triangles les plus grands) au niveau le plus fin (les triangles de base).
- Il n’y a qu’un seul grand triangle de côté 4 : \(N_4^{(4)}=1\) (on a ajouté ici à la notation un exposant entre parenthèses pour indiquer la taille des sous-triangles).
- Le niveau suivant est illustré dans la figure 2 où l’on voit clairement 3 triangles dont les côtés sont de longueur 3.
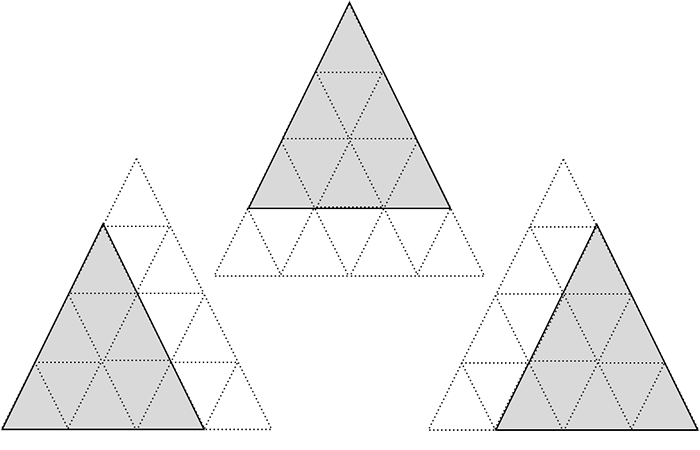
Figure 2 : Les 3 triangles de taille 3 contenus dans le quatrième terme de la suite.
- Les choses deviennent un peu plus compliquées au niveau suivant où l’on distingue 7 triangles (voir figure 3).
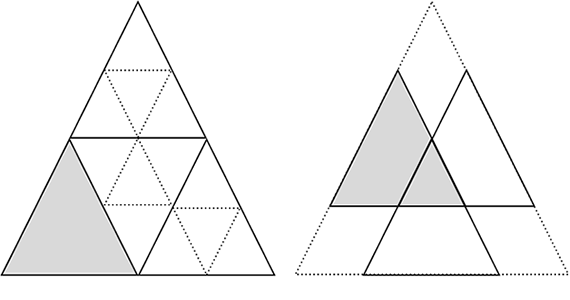
Figure 3 : 4 triangles de côté 2 à gauche (on notera ici un triangle inversé) et 3 à droite (où les triangles se superposent).
- Au niveau des petits triangles de base, une énumération par lignes indique que ce nombre est la somme des 4 premiers nombres impairs. Il s’agit d’une somme bien connue, qui est égale au carré du nombre de ces entiers impairs, ici 42 = 16. On trouvera ci-dessous une façon astucieuse de retrouver ce résultat.
Au total, on a donc \(N_4 = N_4^{(4)}+N_4^{(3)}+N_4^{(2)}+N_4^{(1)}=1+3+7+16=27\).
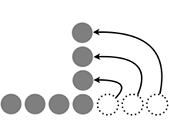
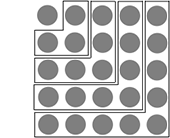
La somme des n premiers entiers impairs est égale à n2. On peut prouver ce résultat en représentant la somme cherchée par des jetons, par exemple, pour n = 5.

Chaque ligne est pliée en son milieu pour obtenir un carré parfait.
Comment généraliser pour une valeur de k quelconque ?
Il est possible de généraliser l’analyse à partir des exemples précédents sur les petites valeurs de k.
Pour chaque triangle de rang k, on a 3 triangles de rang k-1 imbriqués (soit, \(3 N_{k-1}\)).
Chacun de ces triangles de rang k-1 a une partie commune avec les deux autres, c’est un triangle de rang k-2, donc il faut les enlever (ce qui correspond à \(-3 N_{k-2}\)).
Par contre, il y a une partie supplémentaire commune aux trois, c’est un triangle de rang k-3 (soit, \(+ N_{k-3}\)).
Il faut de plus ajouter le grand triangle (\(+1\)).
Et quand k est pair, il y a un triangle supplémentaire de rang k-2 qui apparaît inversé au milieu (donc, dans ce cas \(+1\)).
On arrive ainsi à la formule de récurrence suivante :
Pour k pair : \(N_k = 3 (N_{k-1} – N_{k-2}) + N_{k-3} + 2\)
Pour k impair : \(N_k = 3 (N_{k-1} – N_{k-2}) + N_{k-3} + 1\)
Avec k ≥ 3 et \(N_0 = 0\), \(N_1 = 1\) et \(N_2 = 5\).
Reprenons les valeurs obtenues pour les premiers termes de la suite et allons un peu plus loin dans les valeurs de k en utilisant un algorithme itératif basé sur les expressions précédentes. Les huit premières sont consignées dans le tableau suivant :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 1 | 5 | 13 | 27 | 48 | 78 | 118 | 170 | … |
On peut calculer de proche en proche toutes les valeurs de k plus grandes à partir des expressions de récurrence précédentes ou bien on peut utiliser une astuce. Comme la différence entre deux éléments consécutifs \(N_{k+1}-N_k\) apparait clairement dans les expressions, il est assez naturel d’examiner cette nouvelle suite, puis de nouveau la différence entre deux valeurs consécutives ainsi obtenues. La figure 4 montre ce que l’on obtient en faisant cette opération trois fois de suite.
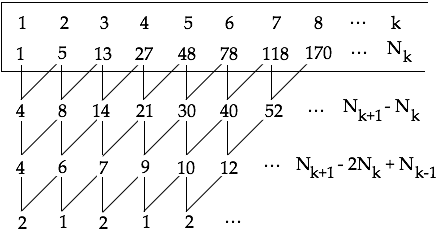
Figure 4 : Tableau des différences de deux termes consécutifs.
La dernière ligne est très régulière (et particulièrement simple) : elle est constituée d’une alternance de 2 et de 1. Et ceci reste vrai pour les valeurs de k aussi grandes qu’on le veuille !
Cette remarque nous permet d’imaginer une solution simple « de proche en proche » qui permet de compléter le tableau quel que soit k en remontant de bas en haut, comme on le voit dans la figure 5 (on obtient \(N_9=235\) en calculant d’abord \(13=12+1\), puis \(65=52+13\) et enfin, \(235=170+65\)). Notons que cette méthode n’apporte conceptuellement rien de plus que l’expression précédente des termes de la suite, mais elle va nous offrir la base pour trouver une expression directe pour calculer \(N_k\).
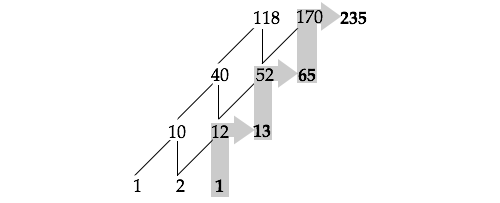
Figure 5 : On obtient la valeur \(N_k=9\) par remontée le long de la diagonale depuis le bas du tableau.
Une solution directe
La solution précédente n’est pas idéale pour les grandes valeurs de k, puisque la construction nécessite d’avoir toutes les valeurs intermédiaires avant de pouvoir calculer un nouveau terme. Une question qui en découle est donc de se demander s’il est possible d’obtenir une expression directe pour \(N_k\) (dans le vocabulaire mathématique, on parle de formule close). La réponse est oui.
Pour ce faire, reprenons le tableau des différences de la figure 4 et concentrons-nous sur les valeurs paires de la dernière ligne. Il est assez facile d’obtenir l’avant-dernière ligne à partir de ces valeurs car \(k=2 \rightarrow 6\), \(k=4 \rightarrow 9\), \(k=6 \rightarrow 12\), \(k=8 \rightarrow 15\)… Pour k=2, on part de la valeur 6 puis on ajoute 3 pour obtenir la valeur du prochain entier pair, etc. C’est-à-dire \(k \rightarrow \frac{3k}{2}+3\). On fait de même pour les valeurs impaires de k : \(k \rightarrow \frac{3}{2}(k+1)+1\). On obtient ainsi des polynômes de degré 1 en k.
On procède de la même manière pour déduire l’expression de la ligne juste au-dessus. L’expression cherchée est un polynôme de degré 2 en la variable k qui dépend de la parité de k et dont la différence entre deux termes consécutifs est donnée par l’expression précédente. Les coefficients sont faciles à calculer par identification à partir des premiers termes connus de la ligne.
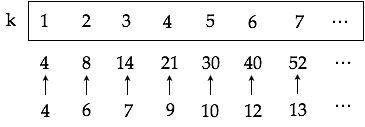
Après quelques manipulations arithmétiques, on obtient :
\(\frac{3k^2+8k+4}{4}\) si k est pair et \(\frac{3k^2+8k+5}{4}\) si k est impair.
On recommence en remontant à la dernière ligne restante pour déterminer l’expression finale de \(N_k\) qui est un polynôme de degré 3 en k, obtenu selon le même principe :
\(N_k = \frac{k.(k+2).(2k+1)}{8}\) si k est pair et \(N_k = \frac{k.(k+2).(2k+1)-1}{8}\) si k est impair.
Pour celles et ceux qui auraient encore des doutes, notons que ces expressions sont facilement vérifiables et démontrables par récurrence.
Arrêtons-nous un moment sur la méthode des différences. La méthode précédente qui consiste à faire le tableau des différences de deux termes consécutifs peut être appliquée à de nombreux autres problèmes, par exemple elle illustre bien la suite des carrés des entiers naturels.
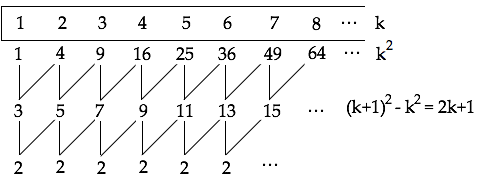
On remonte depuis la ligne du bas où toutes les valeurs sont égales (à 2).
On obtient un nombre impair (2k+1) sur la ligne au-dessus, qui est lui-même la différence entre deux carrés consécutifs ((k+1)2 – k2).
C’est une autre façon de retrouver la propriété précédente que la somme des premiers entiers impairs est égale au carré de leur nombre !
On peut constater que cette méthode n’est pas sans rappeler la construction du triangle de Pascal qui est un outil de base en combinatoire.
Notons également que la machine de Babbage était basée sur les calculs par différences.
Voilà, on peut maintenant obtenir \(N_k\) pour les grandes valeurs de k par un calcul direct, par exemple \(N_{100} = 256275\), ce qui est beaucoup plus court que de le faire à l’aide d’un algorithme itératif ou d’une formule de proche en proche !
Ici, la méthode par différences a été particulièrement fructueuse, mais toute expression récurrente ne peut pas forcément s’exprimer de cette façon-là. Il a fallu faire appel à l’ingéniosité d’une analyse mathématique pour y parvenir, et ceci n’a été possible qu’après avoir posé les équations de récurrence et les avoir organisées sous forme d’algorithme itératif.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Denis Trystram
Professeur à l'Université Grenoble Alpes, chercheur au Laboratoire d'Informatique de Grenoble (LIG, CNRS/Inria/Grenoble INP/Université Grenoble Alpes) dans l'équipe Inria DataMove.
