De Fourier à la 5G

Comment construire un signal portant une information numérique ?

De nombreuses applications de communication font appel par nature à des informations numériques. Dire qu’une information est numérique signifie qu’elle correspond à une suite de nombres d_n prenant un nombre fini de valeurs. Par exemple, dans une image, n peut représenter l’emplacement d’un pixel et d_n son niveau de gris. Dans un texte, n peut représenter l’emplacement d’un caractère dans le fichier et d_n le numéro de chaque lettre de l’alphabet (0 pour « a » et 25 pour « z »). Tout nombre entier pouvant s’écrire comme un nombre binaire, l’information numérique peut toujours se ramener à une suite binaire : d_n prend alors la valeur 0 ou 1. Chaque élément de cette suite sera appelé un bit.

Pour transmettre cette suite binaire, il faut un support de communication. C’est très souvent une onde électromagnétique qui se propage dans un milieu, par exemple dans l’atmosphère comme pour les téléphones mobiles ou dans le verre pour les communications sur fibre optique. Mais cela peut aussi être une onde sonore comme dans les communications sous-marines. Quel que soit le support, la théorie est identique. Dans cet article, par commodité pédagogique, nous prendrons la lumière comme exemple de support.

Dans de nombreux systèmes de communication, on souhaite un débit binaire (nombre de bits transmis en une seconde) qui augmente de génération en génération (il suffit de penser aux téléphones mobiles ou aux connexions Internet actuelles). Pour augmenter ce débit, c’est-à-dire pour transmettre plus de bits en une seconde, il existe deux grandes classes de solutions, l’une jouant sur le nombre de niveaux, l’autre sur la fréquence.

Le principe de départ est de transmettre un bit sur une durée prédéfinie T₀, en décidant d’éteindre la lumière pour un bit ‘0’ et de l’allumer pour un bit ‘1’.

• Une manière simple d’accroître le débit est de transmettre sur la durée T₀ plus que deux valeurs possibles. Par exemple, si on s’autorise 8 niveaux d’intensité de lumière — on parle alors de symboles pour ces niveaux possibles —, on peut transmettre 3 bits sur la durée T₀ ce qui a pour effet de tripler le débit binaire. Évidemment, la fiabilité du système est amoindrie, car la confusion au récepteur entre 8 niveaux est plus facile qu’entre 2 niveaux pour une même consommation énergétique (voir figure 1 ci-dessous).

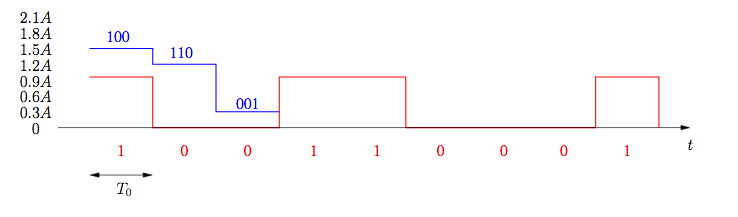
Figure 1 : Suite — 100110001 — émise avec 2 valeurs de symboles possibles (en rouge) ou 8 valeurs de symboles possibles (en bleu).

• L’autre solution est de réduire la durée T₀ entre chaque symbole. On envoie plus de symboles (donc plus de bits) par seconde, ce qui a bien pour effet d’augmenter le débit binaire. Cette seconde solution paraît séduisante et a longtemps été très utilisée. Elle reste d’ailleurs une des méthodes mises en œuvre pour l’augmentation des débits sur la 5G. Elle se heurte néanmoins à une sérieuse limitation présentée ci-dessous.

Avant de continuer, il convient de mentionner que les ondes appartiennent à l’État, qui ensuite les distribue aux différents usages de télécommunications. Or il ne distribue pas des instants temporels (ce serait bien trop compliqué à gérer, notamment en raison d’horloges différentes qui devraient être parfaitement synchrones entre des systèmes indépendants) mais des bandes de fréquences. Ainsi, chaque système ou chaque utilisateur se voit attribuer une bande de fréquences libre pour son propre usage.

Pour passer de l’étude du signal à celle des fréquences intervient une propriété fondamentale établie par Fourier : une fonction périodique se décompose en une somme infinie de fonctions cosinus, et cette propriété peut être étendue à toute fonction temporelle.

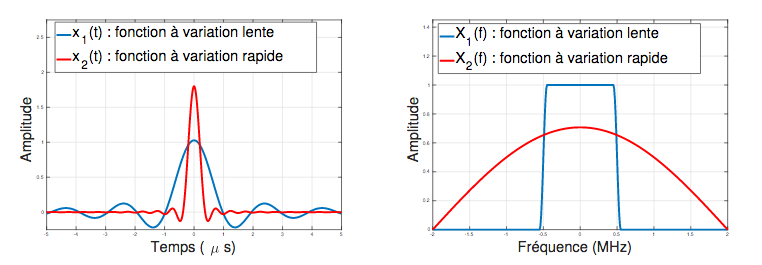
Figure 2 : Fonction \(t\mapsto x(t)\) (à gauche) et son spectre \(f\mapsto X(f)\) (à droite)

Sur la figure 2, on remarque que plus le signal \(x(t)\) a des variations rapides (courbe rouge), plus son spectre, la fonction \(X(f)\) correspondante, est non nul pour une grande plage de valeurs de \(f\).

Comme le montre la figure 2 ci-dessus, l’onde portant l’information varie plus rapidement si T₀ diminue et admet dans ce cas une largeur de bande plus importante. Il faudra donc trouver plus de bandes disponibles. Malheureusement, il arrive souvent que de nombreux systèmes requièrent l’utilisation des mêmes bandes de fréquences (typiquement il y a un embouteillage autour de 1 GHz) en raison de besoins proches en conditions de propagation et en tailles d’antenne. Par conséquent, moins chaque système occupe de bande et plus on pourra faire coexister de systèmes ou d’utilisateurs.

Plus précisément, dans l’atmosphère, un signal porté par une fréquence plus courte, moins atténué que celui porté par une fréquence plus longue, ira plus loin et donc couvrira une plus grande zone géographique. Quant à la taille des antennes, elle est en général inversement proportionnelle à la fréquence.

Ainsi, pour que le signal aille loin, il faut utiliser des petites fréquences, donc de grandes antennes. Or, les signaux variant alors lentement, seuls de faibles débits binaires pourront être atteints. Inversement, pour avoir de grands débits binaires, il faut utiliser des grandes fréquences, ce qui implique de petites antennes. Ceci présente un avantage pour des objets portables. Mais les zones de couverture réduites obligeront à placer des antennes-relais régulièrement, induisant un coût pour les opérateurs.

Gestion de l’interférence

Dans un contexte de communications sans fil, le signal émis \(x(t)\), qui contient les bits d’information, n’arrive souvent pas en ligne droite au récepteur. En effet, on voit rarement l’antenne-relais lorsqu’on utilise son téléphone mobile. En fait, l’onde rebondit sur les différents obstacles (bâtiments, sol, arbres, etc.) avant d’arriver au récepteur.

Le canal de propagation est constitué de \(K\) trajets ou échos (induits par des rebonds) caractérisés par leur atténuation \(a_k\) et leur temps de propagation \(\tau_k\). Notons \(y(t)\) le signal reçu, il se calcule par l’équation (1) :

\[y(t) = \sum_{k=1}^{K} a_k x(t-\tau_k)\]

Ces trajets ont tendance à mélanger les symboles émis entre eux, ce qui induit une interférence entre les bits, donc des erreurs de transmission (voir la figure 3 ci-dessous).

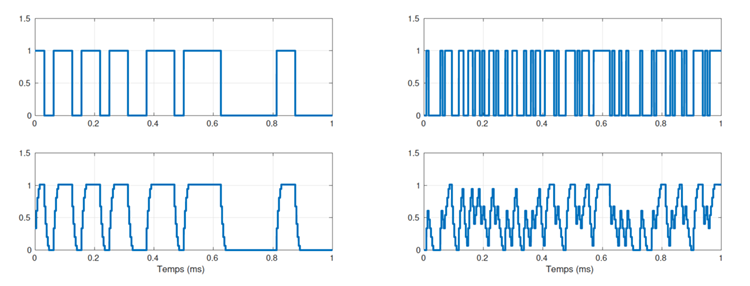
Figure 3 :
Le canal de propagation vaut \(a_1=1\), \(a_2=0,8\), \(a_3=0,6\), \(a_4=0,4\), \(a_5=0,2\) et \(\tau_1= 0 \mu s\), \(\tau_2= 7,81 \mu s\), \(\tau_3= 15,62 \mu s\), \(\tau_4= 23,43 \mu s\), \(\tau_5= 31,25 \mu s\).
Colonne de gauche : signal émis \(x(t)\) avec \(T_0=31,25\mu s\) (en haut), signal reçu \(y(t)\) associé (en bas)
Colonne de droite : signal émis \(x(t)\) avec \(T_0=7,81\mu s\) (en haut), signal reçu \(y(t)\) associé (en bas).

On remarque sur la figure 3 que pour un même canal de transmission, envoyer des bits plus rapidement (colonne de droite) induit une interférence plus forte, puisqu’il est plus difficile de revenir au signal émis.

Néanmoins cette transformation entre \(x(t)\) et \(y(t)\) est très particulière. On vérifie que :

• l’addition des entrées revient à additionner les sorties,
• un retard à l’entrée revient juste à avoir le même retard à la sortie.

Pour l’exprimer sous forme mathématique, notons \(\mathcal{T}\) la transformation telle que \(y(t)= \mathcal{T}(x(t))\).
On vérifie \( \ \mathcal{T}(x_1(t)+x_2(t))= \mathcal{T}(x_1(t))+\mathcal{T}(x_2(t)) \) et \( \ \mathcal{T}(x(t-t_0))= y(t-t_0).\)

Ces deux propriétés confèrent à la transformation \(\mathcal{T}\) le nom de filtrage linéaire.

Ici intervient une deuxième propriété fondamentale en lien avec Fourier : dans le domaine des fréquences, tout filtrage linéaire se réduit à une simple multiplication des amplitudes des transformées de Fourier.

Cette propriété fondamentale 2 est à l’origine du succès de la transformée de Fourier pour l’étude de tout système modélisable par un filtrage linéaire (et ils sont extrêmement nombreux).

Elle est aussi à l’origine d’une technique d’encodage des symboles, appelée OFDM (Orthogonal Frequency Division Multiplexing), existante depuis le milieu des années 1980, qui permet d’éliminer facilement l’interférence observée à l’équation (1).

On a remarqué que quand un symbole est envoyé à un instant particulier, il se mélangeait avec ses voisins (cf. figure 3). En revanche, en examinant attentivement la propriété fondamentale 2, on remarque que si le symbole est envoyé à une fréquence particulière \(f\) en modulant directement \(X(f)\), alors au récepteur, c’est-à-dire sur \(Y(f)\), il ne se mélange pas avec les symboles des fréquences voisines puisque \(Y(f)\) ne dépend que de \(X(f)\). On pourra ainsi éviter l’interférence entre symboles quel que soit le canal et le débit.

Reconsidérons l’exemple de la figure 3 : augmenter le débit peut conduire à diminuer \(T_0\) et donc à augmenter le nombre de symboles interférant entre eux (typiquement \(\tau_{\max}/T_0\) avec \(\tau_{\max}=\max_{k\in\{1,\dots, K\}}\tau_k\)) ce qui nécessite l’utilisation d’une technique éliminant facilement l’interférence comme l’OFDM. Les applications exigeant du haut débit binaire (comme les jeux, la réalité virtuelle) ne sont donc possibles que grâce à l’OFDM et donc la transformée de Fourier.

Cette technique OFDM est maintenant mûre et utilisée dans la plupart des systèmes de télécommunications : 4G, 5G, Wifi (sauf première génération) ou encore TNT. Bref, sans la transformée de Fourier, on se serait arrêté à la 3G, à la première version du Wifi et nous n’aurions pas de télévision numérique hertzienne.

Gestion de plusieurs flux

Un des autres grands problèmes des réseaux sans fil concerne la gestion des divers flux associés aux différents utilisateurs d’une même antenne-relais ou d’un même point d’accès Wifi, ou aux différentes chaînes de télévision d’un même émetteur télé. Alors qu’il est difficile de séparer les flux en temps car il faudrait une horloge commune, il est bien plus simple de séparer les flux en fréquence. Chaque flux utilisera des bandes de fréquences différentes (mais proches, pour que les conditions de propagation ne soient pas trop différentes). On parle alors de système d’accès multiple à répartition fréquentielle (FDMA – Frequency Division Multiple Access). Le même principe est utilisé pour la TNT où chaque chaîne dispose d’une bande de fréquence. Ces bandes sont indiquées sur l’écran de la télévision lors d’une réinitialisation d’un décodeur TNT.

De nouveau, sans notion de spectre et donc sans la transformée de Fourier, les réseaux de télécommunications seraient plus compliqués à mettre en œuvre et moins performants.

Dans des applications prospectives, on imagine des allocations de spectre entre flux plus flexibles (et non comme les chaînes télé qui ont chacune une bande bien précise définie une seule fois) et s’adaptant instantanément à la charge du réseau, aux conditions de propagation. On parle alors de radio cognitive.

Ouverture vers l’optique non linéaire

Les réseaux-cœurs, qui permettent de relier les antennes-relais entre elles ainsi que les serveurs et centres de données du monde entier, sont constitués de liens par fibre optique. La fibre optique arrive aussi maintenant dans les foyers pour améliorer grandement les débits. Ce medium de transmission se comporte différemment de l’atmosphère. Lorsque les puissances utilisées sont faibles, le comportement est un filtrage linéaire et donc ce que nous avons décrit plus haut s’applique. Dans de nombreuses situations (câbles optiques sous-marins entre océans, communications à ultra-haut débit), alors que le nombre de niveaux croît énormément en raison du très haut débit, la puissance émise doit être fortement augmentée afin de limiter la confusion entre les niveaux des symboles. La fibre change alors de comportement et n’est plus un filtrage linéaire, ce qui rend l’utilisation de la transformée de Fourier peu intéressante. Des travaux intenses en mathématiques tentent d’étendre les principes de Fourier dans le but de trouver des variables à travers des transformations qui ne se mélangent pas malgré un filtrage non linéaire. On parle alors de transformée de Fourier non linéaire, même si les équations induites sont très différentes de la transformée de Fourier conventionnelle.