De Fourier à la compression d’images et de vidéos

La transformée de Fourier permet de décrire un signal comme une superposition de formes d’ondes élémentaires, et ainsi de le représenter par les fréquences qui le constituent. Or les images naturelles ne contiennent que quelques fréquences actives, correspondant à des coefficients de Fourier non nuls, et dont le nombre dépend de la complexité de l’image. Par exemple, les régions uniformes de l’image vont être représentées par un faible nombre de coefficients de Fourier alors que les régions de l’image où il y a des discontinuités, par exemple des contours, vont être représentées par un plus grand nombre de coefficients.

Compacter l’information

Ainsi, la transformation permet de compacter l’information sur un faible nombre de fonctions élémentaires, qui suffisent pour représenter tout le signal, d’où la compression. Ce principe fait partie des éléments fondateurs de tout algorithme de compression d’images et de vidéos. Alors que la transformée de Fourier s’appuie sur des fonctions élémentaires sinus et cosinus, il existe une variante, appelée transformée en cosinus discrète (discrete cosine transform ou DCT), qui n’utilise que la fonction cosinus. Cette transformée en cosinus discrète est au cœur de tous les standards de compression JPEG et MPEG depuis 30 ans. Son succès est dû à ses propriétés de bonne compaction de l’information (on parle d’énergie) de l’image sur un faible nombre de fonctions élémentaires. Des algorithmes de calcul rapide de la DCT, analogues aux algorithmes de Cooley et Tukey pour la transformée de Fourier (Fast Fourier Transform ou FFT), ont également été déterminants dans l’adoption de cette transformation dans les algorithmes de compression vidéo au début des années quatre-vingt-dix.

Figure 1 : Décomposition d’une image couleur. Une image couleur (ici image barbara, classiquement utilisée en traitement d’images fixe) contient trois composantes : Rouge Vert Bleu. Une autre représentation, classiquement utilisée en compression, est celle présentée ici avec une composante de luminance Y et deux composantes de Chrominance (Cb et Cr). L’avantage de cette représentation est lié au système visuel humain, qui est plus sensible à la luminance qu’à la chrominance. Ainsi, les composantes Cb et Cr peuvent être représentées avec moins de pixels que la composante Y sans nuire à la perception de l’image.

Une image couleur est formée de trois composantes, une de luminance et deux composantes de chrominance (voir figure 1 ci-dessus). Chaque composante de l’image est découpée en blocs (voir figure 2 ci-dessous). Puis, chaque bloc est décomposé sous forme d’une somme pondérée de fonctions de base.

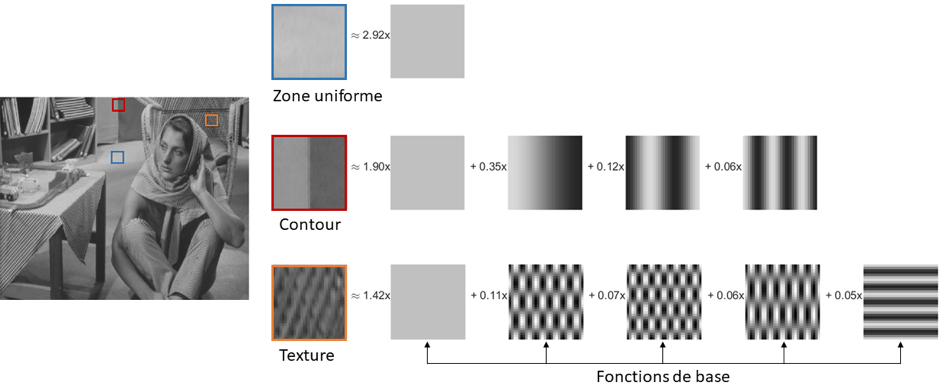
Figure 2 : Décomposition d’une image. L’image est tout d’abord découpée en blocs qui ne se chevauchent pas, puis chaque bloc est décomposé sur les fonctions de base DCT. Pour chaque composante (Y, Cb ou Cr), les blocs sont décomposés sous forme d’une somme pondérée de fonctions de base DCT, dont le nombre varie en fonction de la complexité du bloc (zone uniforme, contour ou texture).

Les coefficients représentant l’image sur l’ensemble choisi de fonctions de base doivent être représentés par un nombre fini (et si possible faible) de valeurs, qui définissent un alphabet de quantification. La transformation de Fourier ne dégrade en rien le signal. En effet, elle change simplement l’espace de représentation d’un domaine pixel vers un domaine fréquentiel. En revanche, la quantification des coefficients est l’opération qui va permettre de comprimer davantage l’information au prix d’une dégradation (on parle de distorsion) maîtrisée.

Exploiter les propriétés du système visuel humain

Il est aussi nécessaire de faire en sorte que les dégradations induites par la quantification ne soient pas perceptibles visuellement. Pour cela, l’opérateur de quantification, et en particulier la taille de l’alphabet de quantification, doit tenir compte des caractéristiques du système visuel humain. Les propriétés du système visuel humain exploitées en compression d’images et de vidéos sont la sensibilité au contraste et les propriétés de masquage. La sensibilité au contraste est la capacité du système visuel à percevoir les changements de luminance ou de couleur dans l’image. La figure 3 (ci-dessous) représente la fonction de sensibilité au contraste et montre que l’on perçoit plus facilement les différences de contraste lorsque la fréquence est faible. Ainsi, la quantification est plus précise (alphabet plus grand) pour les basses que pour les hautes fréquences. Le masquage est l’effet de réduction de la visibilité d’une composante dans une image par la présence d’une autre composante de forte valeur. Ainsi, si la décomposition d’un bloc d’image contient un coefficient de grande valeur (par exemple un contour est très marqué), les variations des coefficients des autres fréquences sont moins visibles et ces coefficients peuvent être quantifiés de manière moins précise.

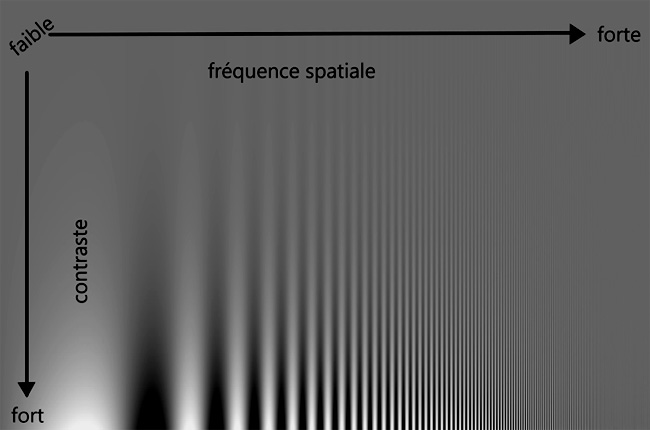
Figure 3 : Sensibilité au contraste. Cette figure montre des motifs dont la fréquence croît vers la droite, et dont le contraste (i.e. l’amplitude) croît vers le bas. Les différences de contraste sont perçues plus facilement quand la fréquence est faible. Issue de travaux de F. W. Campbell et J. G. Robson, cette figure a été générée à partir d’une image de I. Ohzama.

Quant à la figure 4 (ci-dessous), elle illustre un exemple où plus d’erreurs de quantification ont été introduites au niveau des contours de l’image, et que ces dégradations sont peu visibles.

Figure 4 : Masquage des erreurs de compression par les contours et la texture de l’image ; image d’origine (gauche) ; image comprimée (milieu) ; erreurs résultant de la compression se situant surtout sur les contours.

Les coefficients quantifiés de la transformée doivent ensuite être représentés par des séquences aussi courtes que possible d’éléments binaires (les « bits »). Cette opération, appelée codage entropique, repose sur la théorie de l’information de Shannon, et exploite les propriétés statistiques des coefficients quantifiés. L’objectif est de coder ces coefficients quantifiés avec un débit proche de leur « entropie », c’est-à-dire en supprimant toute forme de redondance dans la séquence binaire transmise. Les coefficients quantifiés sont alors représentés par des suites de bits (appelées mots de code) ayant des longueurs variables. Diminuer le nombre de bits nécessaire pour représenter l’image tout en maîtrisant la distorsion apportée par la quantification fait appel à des méthodes d’optimisation dites débit-distorsion (le débit ici est le nombre de bits par pixel). Ces suites de bits constituent la version comprimée de l’image, soit le contenu des fichiers JPEG ou MPEG. Afin de reconstituer l’image, la suite de bits subit les opérations inverses de celles utilisées pour la compression : décodage entropique, transformée en cosinus discrète inverse.

De la transformée de Fourier à des transformées apprises

La compaction de l’information présente dans une image ou une vidéo est d’autant plus efficace que les fonctions élémentaires sont bien adaptées au signal à comprimer. De l’utilisation de fonctions prédéfinies comme celles de la transformée de Fourier ou en Cosinus Discrète, la recherche en compression s’est naturellement tournée vers l’apprentissage de ces fonctions élémentaires à partir d’ensemble d’images d’entrainement. Les fonctions apprises peuvent être vues comme des éléments de texture stockés dans un dictionnaire. Cet apprentissage a été rendu possible grâce à l’évolution des puissances de calcul mais aussi grâce à l’explosion du nombre de contenus images et vidéos sur Internet et les réseaux sociaux. Les réseaux de neurones datant des années soixante ont pris une ampleur considérable ces dernières années avec l’apparition de nouvelles architectures et en particulier de réseaux de neurones profonds. Grâce aux puissances de calcul et aux volumes de données aujourd’hui disponibles, ces réseaux ont ouvert la voie à de nombreux champs d’application, y compris en vision et en compression d’images. Ces réseaux, en particulier les réseaux appelés auto-encodeurs, permettent d’apprendre des fonctions correspondant à des transformations non linéaires. Étant mieux adaptées aux données, ces fonctions fournissent des représentations plus compactes que celles obtenues avec les fonctions élémentaires comme les transformées de Fourier et en cosinus.

De nouveaux défis avec l’arrivée de la haute définition

Les deux dernières décennies ont été également marquées par l’apparition de dispositifs de capture et de visualisation d’images et de vidéos au format haute définition, voire ultra haute définition (UHD), posant de nouveaux défis à la compression d’images en raison des très grands volumes de données que ces formats génèrent. Pour ne donner que quelques exemples, une vidéo au format HD (1920×1080 à 25Hz) a un débit non compressé de 593 Mbs (Mégabits par seconde), qui peut être réduit à 2 Mbs avec la dernière norme de compression MPEG5 adoptée en 2013. Soit une division du débit par 300 ! La visualisation en relief ou la visualisation immersive sont également maintenant possibles grâce aux nouveaux dispositifs de capture et de rendu des images stéréo, multivues ou 360 degrés. Au-delà des volumes de données de plus en plus élevés, ces signaux contiennent une information sur la géométrie à trois dimensions (3D) de la scène qui peut être représentée sous forme de nuages de points ou de maillages en trois dimensions. La compression de ces signaux fait aussi appel à des transformations ou décompositions en fonctions élémentaires, selon les principes fondateurs de la transformée de Fourier qui restent toujours d’actualité. Cette fois, les fonctions élémentaires représentent des variations (fréquences) du signal sur ces nuages de points ou ces maillages et non plus sur des ensembles de pixels.