De la transformée de Fourier à l’imagerie médicale

Même si le principe de la transformée de Fourier a maintenant 150 ans, rappelons que tout ce que nous allons aborder dans cet article n’est possible que depuis quelques dizaines d’années. En effet, la transformée de Fourier (TF) ou plus exactement son homologue numérique (la Fast Fourier Transform également appelée FFT) est une méthode d’étude des signaux et images assez simple à mettre en œuvre sur des ordinateurs, très peu gourmande en temps de calcul et aussi très stable, ce qui est un atout très important en informatique ; c’est-à-dire que des signaux « très semblables » ont des TF « très semblables ».

Pendant des dizaines d’années, la rapidité de cette FFT a énormément contribué au développement de l’imagerie. Exception faite de vos vieilles radios, la TF a sans doute été utilisée dans presque toutes les images médicales que vous avez pu voir dans votre vie. De nos jours, si le temps de calcul pour la reconstruction des images radiologiques n’est plus un problème, les difficultés se concentrent plutôt sur la nécessité de diminuer le temps passé par le patient dans la machine pendant l’acquisition des données : la puissance de calcul des ordinateurs actuels permet désormais d’utiliser des techniques d’acquisition du signal plus rapides qui, en contrepartie, imposent des méthodes de reconstruction beaucoup plus complexes et lentes que la seule transformée de Fourier.

Pour aider à comprendre l’apport de la TF, en particulier dans le monde de l’Imagerie par Résonance Magnétique (IRM), nous allons faire quelques digressions en parlant par exemple d’une manière très pragmatique d’interpréter la transformée de Fourier : c’est un outil très pratique pour scruter les dimensions inverses.

Transformée de Fourier et dimensions inverses

La TF peut être vue comme un outil mathématique permettant de passer d’une base de représentation à une autre. Elle contient dans sa définition une fonction appelée fonction exponentielle qui doit s’appliquer sur des nombres sans dimension (c’est-à-dire sans unité de mesure, comme un quotient de deux longueurs par exemple), et c’est là l’un des plus beaux « secrets » de la TF : si on l’applique par exemple à une fonction décrite au cours du temps et donc mesurée en secondes [s], l’exponentielle contient alors un facteur qui est dimensionné en secondes. Pour qu’elle reste sans dimension, l’exponentielle doit donc incorporer un autre facteur dimensionné en inverse de secondes, c’est-à-dire en Hertz.

Cette contrainte mathématique permet de garder l’exponentielle de la TF sans dimension, mais elle a aussi pour effet de rendre le résultat d’une TF d’une dimensionnalité inverse de celle de la fonction qui lui est donnée en entrée.

De l’intérêt de changer de base de représentation

Passer d’une base de représentation à une autre est une technique classique pour simplifier l’analyse de certains processus. Faire la TF de quelque chose ne change pas ce qu’est cette chose mais agit uniquement sur la manière de représenter cette chose. Par exemple, dans une colonie d’oiseaux, très souvent les parents sont incapables de reconnaître visuellement leurs petits, car les poussins sont trop semblables (un physicien vous dirait avec beaucoup d’aplomb que la base de représentation spatiale n’est pas adaptée à la détection du poussin). Heureusement, les oiseaux repèrent très facilement leurs petits par leurs cris car, vous pourrez le ressortir en société : « c’est la représentation acoustique du poussin qui est la plus utile aux parents ».

Source : xkcd

De la même manière, la TF d’une image de la vie réelle n’est pas parlante du tout, car nos yeux sont faits pour analyser notre environnement à travers l’espace métrique ; ils ont l’habitude d’analyser des groupes de points colorés. Si on nous montre la TF de notre chat (c’est-à-dire sa représentation dans l’espace inverse de notre espace habituel), on peut avoir une certaine difficulté à le reconnaître. Par contre, dans le cadre de la résonance magnétique nucléaire (RMN) et plus particulièrement dans celui de l’imagerie par résonance magnétique (IRM), le signal acquis est très difficile à interpréter dans sa forme brute tandis que sa TF nous permet de remettre son contenu sous une forme « parlante à nos yeux ».

Quelle est donc la source de cet étrange signal IRM, pourquoi est-il déjà dans l’espace inverse, pourquoi la TF de mon chat dans une IRM ressemble-t-elle réellement à mon chat ?

Pour répondre à ces questions fondamentales, nous allons maintenant nous pencher sur les principes de la Résonance Magnétique Nucléaire.

Le signal RMN

La RMN a commencé à être utilisée dans les années cinquante lorsque des chercheurs se sont aperçus que certaines molécules plongées dans un champ magnétique intense absorbaient les champs radiofréquences (RF) qu’on leur appliquait à des fréquences bien précises.

Que se passait-il donc ? Ils avaient découvert que, lorsque des molécules sont plongées dans un champ magnétique, certains noyaux de leurs atomes se magnétisent et se comportent un peu comme des boussoles qui indiquent la direction du champ magnétique dans lequel elles sont plongées. Quand ils envoyaient des champs RF, ils apportaient de l’énergie à ces noyaux qui l’absorbaient et la restituaient en faisant « tourner » leurs aimantations. Dans le cas des noyaux, la fréquence de rotation des aimantations dépend de l’intensité du champ magnétique dans lequel baignent les noyaux : plus le champ est fort, plus l’aimantation « tourne » vite. Les chercheurs ont ensuite démontré que l’énergie était absorbée à des fréquences précises, car les noyaux présents dans une molécule ne perçoivent pas forcément tous le même champ magnétique : suivant leur emplacement au sein de la molécule, ils vont parfois être très exposés au champ magnétique global et d’autres fois, ils vont en être protégés. Si un noyau est bien protégé du champ magnétique, il va subir un champ magnétique plus faible et absorber des fréquences plus basses que des noyaux subissant le champ magnétique « de plein fouet ». Ce blindage naturel des noyaux d’une molécule est une véritable signature de cette molécule. Les chimistes utilisent encore quotidiennement ce principe pour savoir si les molécules qu’ils synthétisent sont bien celles qu’ils pensent.

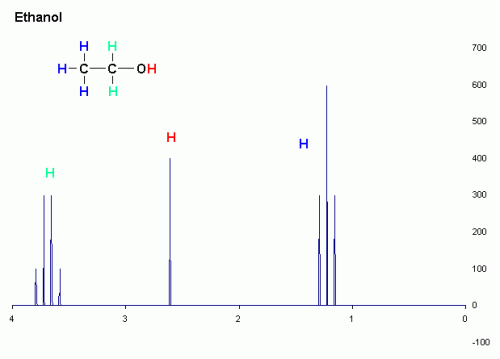
Spectre RMN ¹H de l’éthanol. Crédit Image T. Vanschaik [CC BY-SA 3.0]

Là où la TF entre dans la danse

Au début, les RMN-istes scannaient les échantillons fréquence par fréquence en regardant les fréquences absorbées (comme lorsqu’on « scanne » toutes les fréquences de son poste radio pour trouver les stations). Cette méthode fonctionnait bien mais était plutôt lente.

Un jour, ils ont eu l’idée d’utiliser la TF : « si l’information qui nous intéresse (celle qui parle à nos yeux) est une représentation de l’intensité d’un signal en fonction de sa fréquence, c’est exactement ce que la TF permet d’obtenir à condition que l’on puisse lui fournir une fonction représentant l’intensité du signal en fonction du temps ». Observer un signal au cours du temps, on savait déjà très bien le faire, les RMN-istes ont donc inventé un système permettant de déposer de l’énergie uniformément sur tous les noyaux concernés et d’enregistrer ensuite au cours du temps le signal restitué par les noyaux lorsqu’ils font tourner leur aimantation. Charge à la TF de faire le tri en synthétisant un spectre fréquentiel. La RMN impulsionnelle était née (c.f. vidéo 1).

 Le graphe 1 (à gauche) décrit, en bleu sur le premier graphe, des aimantations en rotation à des fréquences données. L’intensité de chaque aimantation est fonction du nombre de noyaux présents à chaque fréquence. Les intensités décroissent au cours du temps à mesure que les aimantations perdent leur énergie. En rouge, on observe sur le même graphe le signal total généré par toutes ces aimantations en rotation.

Le graphe 2 (à droite) montre l’intensité du signal total acquis au cours du temps : c’est le signal acquis en RMN à l’aide d’une antenne radiofréquence.

Quant au graphe 3, il montre la transformée de Fourier du signal acquis. Alors que le signal acquis au cours du temps « ne ressemble à rien », l’interprétation du spectre est triviale : les raies sont réparties en fonction de leur fréquence et leur intensité relative correspond aux proportions de noyaux à chaque fréquence.

L’imagerie par résonance magnétique

Quelques dizaines d’années plus tard, les RMN-istes se sont dit : « jusqu’à présent nous avons subi le bon vouloir des molécules, c’est elles qui dictent quelles sont les fréquences présentes dans le signal que l’on acquiert. Si l’on arrivait à faire en sorte que l’intensité du champ magnétique dans lequel les aimantations sont plongées varie aussi (surtout) en fonction de la position spatiale de chaque aimantation, alors le signal observé dépendrait aussi (surtout) de leur position spatiale ». Ils ont donc fabriqué ce qu’ils ont appelé des bobines de gradients qui permettent de changer linéairement l’intensité du champ magnétique en fonction de la position. L’IRM était née (c.f. vidéo 2).

Sur cette seconde animation, les aimantations (toujours en bleu) sont regroupées en différentes régions de l’espace et un gradient de champ magnétique a été ajouté suivant la direction gauche-droite. Ainsi, plus les aimantations sont à droite et plus elles tournent vite (dans la direction haut-bas, elles ont toutes la même vitesse). L’aimantation rouge représente toujours la somme de toutes les aimantations. Le graphe 2 représente toujours l’acquisition du signal total au cours du temps. Le graphe 3 représente (toujours) la TF de ce signal qui dans ce cas, représente l’intégrale des aimantations en fonction de leur fréquence, c’est-à-dire, la projection 1D des aimantations suivant la direction du gradient.

Il est difficile de décrire en quelques lignes le véritable Big Bang créatif qui a suivi, mais on peut souligner que la recherche en IRM s’est littéralement polarisée autour de la notion de l’espace inverse : comment l’acquérir le plus fidèlement possible ? le plus rapidement possible ? le plus intelligemment possible ? Quel est le meilleur moment pour acquérir quelle partie du signal ? etc. La technique IRM s’est extrêmement complexifiée : les images d’aujourd’hui sont plus belles, mieux résolues, elles peuvent donner énormément d’informations sur les tissus, s’ils sont irrigués, s’ils reçoivent de l’oxygène, si ces tissus sont durs ou mous, s’ils sont riches ou non en certaines molécules… Mais, aujourd’hui encore, les images IRM sont reconstruites par une Transformée de Fourier qui va transformer l’étrange signal de l’espace inverse en quelque chose « qui parle aux yeux des médecins » (c.f. vidéo 3).

Cette dernière animation décrit dans un cas beaucoup plus proche du réel, la manière dont le signal IRM peut être acquis au cours du temps. Nous voyons aussi en parallèle à quoi ressemble l’espace image au fur et à mesure que l’espace inverse est échantillonné par l’IRM.

Conclusion

Pendant toutes ces années, la transformée de Fourier a été considérée à raison comme l’alpha et l’oméga. C’est à elle que l’on doit tous ces immenses progrès en imagerie médicale. Puis, il y a quelque temps sont apparues des techniques révolutionnaires d’imageries RMN qui transgressaient les règles et limitations imposées par la Transformée de Fourier : les scientifiques venaient de redécouvrir que la Transformée de Fourier peut aussi être simplement considérée comme une méthode très élégante de résolution d’un certain type de systèmes d’équations linéaires. Pour de très bonnes raisons, durant toutes ces années, nous avons travaillé sur les moyens de faire en sorte que le signal acquis puisse être reconstruit en prenant « l’autoroute » sûre et rapide qu’est la Transformée de Fourier. Ces chercheurs sont venus nous rappeler l’existence de toutes les routes secondaires qui ont leurs règles à elles et qui mènent aussi à de très jolis endroits.