Des peptides à explorer
Les protéines sont l’un des constituants des cellules, qui est essentiel à leur fonctionnement. Elles sont, en général, synthétisées au sein des cellules via le processus de transcription de l’ADN en ARN, suivi de la traduction de cet ARN en protéine, effectuée par les ribosomes. Les protéines ainsi produites sont linéaires, formées de quelques dizaines à plusieurs milliers d’acides aminés réunis par des liaisons peptidiques. Une vingtaine d’acides aminés différents sont utilisés. Les acides aminés peuvent ainsi être vus comme des maillons, de vingt sortes différentes, assemblés pour former des chaînes plus ou moins longues qui ne sont jamais fermées, les protéines.
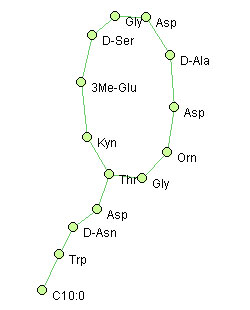
Représentation de la daptomycine, un peptide non-ribosomique.
Cependant, il existe des peptides, de petites protéines, qui ne sont pas synthétisés par la voie classique, mais par de gros complexes enzymatiques appelés synthétases non-ribosomiques. Ces enzymes captent des acides aminés dans le milieu cellulaire et catalysent la formation d’une liaison chimique, peptidique ou non, entre plusieurs acides aminés, pour former un peptide appelé peptide non-ribosomique. Ainsi, ces peptides présentent des particularités qui les distinguent des protéines « classiques ».
Quelles sont ces particularités ? En premier lieu, une plus grande diversité d’acides aminés est incorporée dans ces peptides, ainsi que d’autres types de composés chimiques tels que des lipides ou des glucides. Jusqu’à présent, plus de 500 composés chimiques différents ont été observés dans la composition des peptides non-ribosomiques.
En plus de la diversité de leur composition, les peptides non-ribosomiques présentent des structures particulières. En effet, des structures complexes contenant des cycles ou des branchements peuvent être formées. En reprenant l’analogie précédente, dans le cas des peptides non-ribosomiques, plus de 500 maillons différents sont disponibles pour former de petites chaines pouvant être ou non fermées et, éventuellement, comporter des chaines latérales.
Enfin, ces peptides présentent un intérêt particulier du fait de leurs activités biologiques. Certains de ces peptides servent dans le domaine médical, comme la pénicilline, ou la daptomycine (commercialisée sous le nom de Cubicin) qui sont des antibiotiques, ou encore la cyclosporine qui est un immunosuppresseur utilisé après une greffe. Malgré l’exploitation industrielle d’un certain nombre de ces molécules, leur mode de synthèse est encore peu connu de la communauté scientifique. De nombreuses expériences sont encore nécessaires pour mieux les connaître et, ainsi, mieux exploiter leur potentiel.
C’est pourquoi il a été décidé en 2006 de constituer une base de données, avec une interface web, dédiée aux peptides non-ribosomiques. Cette base s’appelle Norine, Nor pour « non-ribosomal peptides » et ine car les noms de ces peptides se terminent souvent par le suffixe « -ine ». Entre autres informations sur les peptides qu’elle contient, elle offre une représentation de ces peptides sous la forme de graphes d’acides aminés.
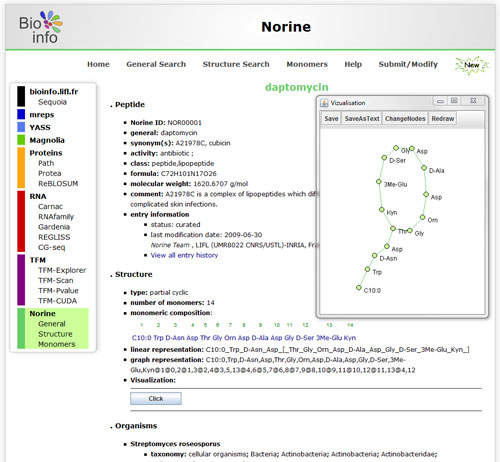
Interface web de la base de données Norine.
Graphe de l’eurypamideB.
Le graphe d’un peptide est composé de nœuds étiquetés par le nom des acides aminés qui le composent et d’arêtes qui représentent les liaisons chimiques entre ces acides aminés. Cette représentation permet à la fois de modéliser le mode de synthèse des peptides non-ribosomiques, par l’ajout successif d’acides aminés, et de se rapprocher de la représentation des protéines classiques, qui est une succession d’acides aminés.
Mais les particularités des peptides non-ribosomiques rendent nécessaire le développement d’outils spécifiques pour leur analyse. Certains de ces outils font appel à l’algorithmique des graphes. En particulier, il a été conçu un algorithme de recherche d’un graphe spécifique parmi les graphes de la base de données.
Pourquoi concevoir un algorithme de recherche d’un graphe dans la base de données Norine ?
Norine contient plus de 1000 peptides non-ribosomiques. Cette base est régulièrement mise à jour, lorsque de nouveaux peptides sont découverts. Pour savoir si un peptide décrit dans un article scientifique est vraiment nouveau ou bien s’il s’agit d’un peptide déjà connu, mais découvert dans de nouvelles conditions expérimentales (autre organisme producteur, autre milieu de culture…), il est nécessaire de comparer le peptide en question à tous les peptides répertoriés dans Norine.
Comparer des graphes dont les structures sont variées n’est pas facile. L’œil humain est très performant pour cela, car il est capable d’identifier rapidement les points communs et les différences flagrantes entre deux dessins, et donc entre deux graphes. Mais à l’échelle d’une base de données, cette procédure ne peut pas être réalisée à la main. Il est nécessaire d’écrire un programme qui réalise cette comparaison, et cela est loin d’être trivial.
Pour commencer, il faut décrire à l’ordinateur le graphe lui-même. Sans entrer dans les détails, cela est réalisé en indiquant, pour chacun des nœuds, ses voisins, c’est-à-dire les nœuds qui lui sont reliés par une seule arête. L’ordinateur n’a donc pas une vision globale du graphe. Un parcours des différentes arêtes est nécessaire pour l’explorer en totalité. Pour comparer deux graphes, il faut donc les explorer en parallèle, en vérifiant à chaque fois si le nœud actuel du premier graphe porte bien la même étiquette que le nœud actuel du deuxième graphe, puis si tous leurs nœuds voisins portent bien les mêmes étiquettes, et ainsi de suite. Cela peut prendre du temps, étant donné qu’il faut commencer par trouver deux nœuds ayant des étiquettes identiques.
De plus, le processus est complexifié du fait que la découverte de nouveaux peptides peut mener à la détermination de structures incomplètes. Par exemple, le composé chimique présent à une position du peptide n’a pas pu être déterminé (un « X » est écrit à cette position) ou il y a une liste d’acides aminés possibles (les différents acides aminés sont indiqués, séparés par des « / ») ; ou bien encore, une partie de la structure complète du peptide n’a pas pu être déterminée.
Le problème revient donc à comparer une structure partielle, représentée sous la forme d’un graphe, à toutes les structures des peptides de Norine, eux aussi représentés par des graphes, pour déterminer si cette structure partielle est présente dans un ou plusieurs de ces peptides. Les chercheurs en algorithmique des graphes connaissent bien ce problème qui consiste à rechercher le sous-graphe commun maximal de deux graphes et l’ont caractérisé comme étant NP-complet. Cela ne signifie pas qu’il faille renoncer à le résoudre mais que, sans la mise au point d’un algorithme spécifique adapté, la recherche d’un graphe partiel dans Norine pourrait prendre plusieurs heures, ce qui n’est pas envisageable pour un site web interactif.
Rechercher une structure partielle dans Norine n’a pas pour seul intérêt la mise à jour de la base. En effet, les peptides qui contiennent des structures partielles communes sont susceptibles de présenter des propriétés proches. Lorsqu’un scientifique découvre un nouveau peptide par étude des molécules présentes dans le milieu de culture d’un micro-organisme, il peut rechercher ce peptide dans Norine en le représentant sous la forme d’un graphe partiel. Ainsi, il peut prédire que les propriétés connues pour les peptides de Norine qui contiennent la structure partielle seront les mêmes ou proches de celles du nouveau peptide. Ces informations l’aideront à orienter les expériences d’étude du nouveau peptide.
Il est également possible de prédire des peptides à partir de l’analyse bio-informatique des synthétases qui produisent les peptides non-ribosomiques. Ici aussi, la recherche dans Norine du peptide prédit peut permettre d’affiner la prédiction, et d’orienter les expériences d’étude du peptide nécessaires à la confirmation de son existence sous la forme prédite.
Ces différentes raisons ont conduit à la conception d’un algorithme de recherche d’un graphe partiel dans un ensemble de graphes complets, prenant en compte les spécificités des structures des peptides non-ribosomiques.
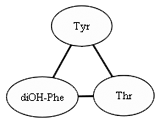
L’objectif est de trouver une structure partielle au sein de structures réelles, quelle que soit la forme de ces structures. Par exemple, il est possible de rechercher la structure partielle représentée dans la figure ci-dessous. Il s’agit d’une structure linéaire, constituée de trois composés chimiques dont un qui n’a pas été déterminé.

Motif à retrouver dans les différents peptides.
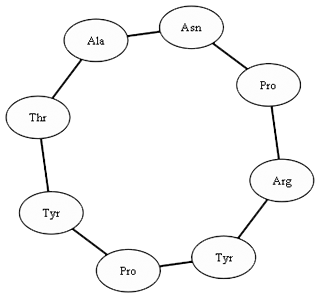
Cette même structure partielle est trouvée dans différents peptides présents dans Norine, dont la cyclonelline, l’eurypamide B et la didemnine N. Essayez de trouver la structure partielle dans ces peptides, puis vérifiez vos hypothèses en cliquant sur le graphe de chaque peptide pour visualiser sa position.
 |
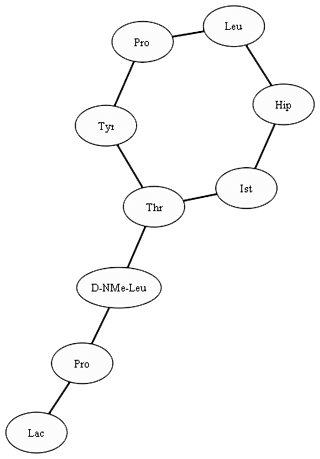 |
| Graphe de la cyclonelline. |
|
 |
|
| Graphe de l’eurypamide B. | Graphe de la didemnine N. |
La structure partielle est donc bien trouvée dans des peptides de structures différentes : un peptide cyclique constitué de huit composés chimiques, un autre peptide cyclique constitué uniquement de trois composés (le peptide partiel formerait donc un cycle et non une ligne) et, enfin, un peptide formé d’un cycle avec un branchement. Le peptide partiel peut, dans ce cas, se placer à différentes positions.
Comment comparer rapidement un graphe partiel à tous les graphes de Norine ?

Motif à rechercher.
L’algorithme qui vérifie si une structure partielle est contenue dans une structure réelle comprend trois étapes. Pour illustrer cet algorithme, la recherche de la structure partielle de la figure ci-contre dans la didemnine N va être utilisée.

Graphe de la didemnine N.
À chaque étape, vous pourrez vérifier sur cet exemple si vous avez bien compris le déroulement de l’algorithme.
Pour une recherche dans la base complète, l’algorithme est appliqué successivement à chaque peptide de Norine.
Vérification préliminaire
Avant de commencer la recherche, il faut s’assurer que la structure réelle est au moins aussi grande que la structure partielle. Si c’est le cas, la recherche de correspondance entre la structure partielle et au moins une partie de la structure réelle peut commencer. Sinon, la structure partielle ne peut pas être présente dans la structure réelle. Le programme passe alors à la structure réelle suivante.
Première étape
La première étape consiste à vérifier si les acides aminés de la structure partielle sont tous présents dans la structure réelle. Pour cela, chaque nœud de la structure partielle est associé, si c’est possible, à au moins un nœud de la structure réelle. Voici les deux règles qui doivent être respectées pour associer deux nœuds :
- Les acides aminés de ces nœuds doivent être identiques. Il ne faut pas oublier qu’une structure partielle peut comporter des nœuds qui représentent plusieurs acides aminés. Ainsi, un nœud d’une structure partielle avec des incertitudes peut être associé à plusieurs nœuds d’une structure réelle. Par exemple, si le premier nœud de la structure partielle est un « X », il va être associé à chacun des nœuds du peptide, c’est-à-dire ici à 9 acides aminés.
- Le nombre d’arêtes du nœud de la structure partielle est inférieur ou égal au nombre d’arêtes du nœud correspondant de la structure réelle. Par exemple, le nœud qui porte l’étiquette « Thr » dans la didemnine N possède trois arêtes, car il y a un branchement. Il est tout de même associé au nœud « X » qui ne possède qu’une arête, car il est présent dans une structure partielle.
Ainsi, un ensemble de nœuds compatibles est construit. Il constitue un nouveau graphe qu’on appelle graphe de compatibilité (abrégé en GC). Chaque paire de nœuds compatibles (un nœud de la structure partielle associé à un nœud de la structure réelle) forme un nouveau nœud dans ce graphe. Nous parlerons par la suite de nœud du GC.
Essayez de reconstituer par vous-même les nœuds du graphe de compatibilité entre la structure partielle (voir le schéma « motif à rechercher ») et la didemnine N, avant de regarder la figure récapitulative ci-dessous.
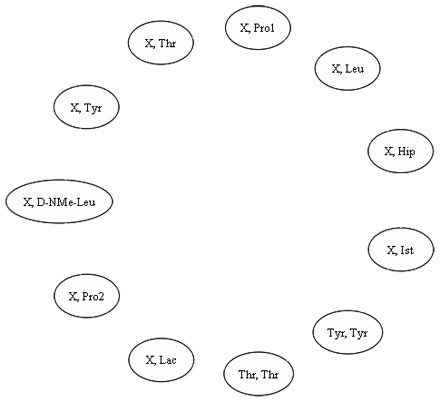
Nœuds du graphe de compatibilité entre la structure partielle et la didemnine N.
Si tous les nœuds de la structure partielle ne sont pas associés à au moins un nœud de la structure réelle, alors la recherche peut s’arrêter. En effet, dans ce cas, il est impossible que la structure partielle soit contenue dans la structure réelle. Par contre, si tous les nœuds de la structure partielle sont présents dans la structure réelle, il faut ensuite vérifier si les arêtes des deux graphes correspondent. Cela est fait lors de la deuxième étape.
Deuxième étape
Comme évoqué précédemment, comparer la forme de deux graphes n’est pas facile et peut prendre beaucoup de temps. Une solution est de regarder par quel chemin il faut passer pour aller d’un nœud à un autre. Plutôt que de comparer des chemins, il est plus efficace de comparer la taille de ces chemins. Nous allons donc calculer la taille des chemins possibles entre toutes les paires de nœuds du graphe partiel, ainsi qu’entre les paires de nœuds du graphe réel. En cas de cycle dans un graphe, nous ne considérons que les chemins élémentaires, c’est-à-dire sans boucle.
Par exemple, entre les nœuds « X » et « Tyr » du graphe partiel, il y a un seul chemin possible de taille 2 (en passant par le nœud « Thr »). Par contre, entre les nœuds « Thr » et « Hip » de la didemnine N, il y a deux chemins possibles, l’un de taille 2 (en passant par le nœud « Ist » ) et l’autre de taille 4 (en passant par les nœuds « Tyr », « Pro » et « Leu »).
Les tableaux suivants récapitulent les tailles des chemins élémentaires pour le graphe partiel et ceux de la didemnine N. Calculez par exemple le ou les chemins élémentaires possibles entre les nœuds « Tyr » et « D-Nme-Leu » de la didemnine N, avant de regarder la solution.
| X | Thr | Tyr | |
|---|---|---|---|
| X | 0 | 1 | 2 |
| Thr | 0 | 1 | |
| Tyr | 0 | ||
| Taille des chemins élémentaires dans le graphe partiel. | |||
| Ist | Hip | Leu | Pro1 | Tyr | Thr | D-Nme-Leu | Pro2 | Lac | |
|---|---|---|---|---|---|---|---|---|---|
| Ist | 0 | 1, 5 | 2, 4 | 3, 3 | 4, 2 | 5, 1 | 6, 2 | 7, 3 | 8, 4 |
| Hip | 0 | 1, 5 | 2, 4 | 3, 3 | 4, 2 | 5, 3 | 6, 4 | 7, 5 | |
| Leu | 0 | 1, 5 | 2, 4 | 3, 3 | 4, 4 | 5, 5 | 6, 6 | ||
| Pro1 | 0 | 1, 5 | 2, 4 | 3, 5 | 4, 6 | 5, 7 | |||
| Tyr | 0 | 1, 5 | 2, 6 | 3, 7 | 4, 8 | ||||
| Thr | 0 | 1 | 2 | 3 | |||||
| D-Nme-Leu | 0 | 1 | 2 | ||||||
| Pro2 | 0 | 1 | |||||||
| Lac | 0 | ||||||||
| Taille des chemins élémentaires dans la didemnine N. | |||||||||
Des chemins de même taille entre deux nœuds du graphe partiel et deux nœuds du graphe réel associés dans le graphe de compatibilité représentent une structure équivalente. Cela signifie que la structure partielle est compatible avec la structure réelle. Nous pouvons donc tracer une arête entre le nœud du GC qui correspond au début du chemin et celui qui correspond à la fin.
Par exemple, le nœud « X » du graphe partiel est associé au nœud « D-NMe-Leu » de la didemnine N. Il en est de même pour les nœuds « Thr » du graphe partiel et de la didemnine N. Vous pouvez constater qu’il n’y a qu’un seul chemin de taille 1 entre « X » et « Thr » d’une part et les nœuds « D-NMe-Leu » et « Thr » d’autre part. Nous traçons donc une arête entre les nœuds « X, D-NMe-Leu » et « Thr, Thr » du graphe de compatibilité.
Dans le cas où il existe plusieurs chemins possibles entre deux nœuds, il faut que les différents chemins possèdent la même taille dans un graphe et dans l’autre. Mais, comme le graphe partiel peut contenir moins d’arêtes que le graphe réel, nous autorisons que le graphe réel comporte plus de chemins entre deux nœuds que le graphe partiel.
Par exemple, le nœud « X » du graphe partiel est associé au nœud « Leu » de la didemnine N. Il en est de même pour les nœuds « Tyr » du graphe partiel et de la didemnine N. Vous pouvez constater qu’il n’y a qu’un seul chemin, de taille 2, entre « X » et « Tyr ». Par contre, il y a un chemin de taille 2 et un chemin de taille 4 entre les nœuds « Leu » et « Tyr » de la didemnine N. Comme le chemin du graphe partiel est présent parmi les chemins de la didemnine N, nous traçons une arête entre les nœuds « X, Leu » et « Tyr, Tyr » du graphe de compatibilité.
À vous de jouer : tracez les arêtes du graphe de compatibilité en fonction des tailles des chemins élémentaires calculées précédemment. Sur l’applet ci-dessous, pour tracer une arête, cliquez sur ses deux extrémités. Vous pouvez ensuite vérifier vos hypothèses ou afficher la solution. Un indice : il y a sept arêtes à trouver.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
En comparant les tailles des chemins élémentaires entre toutes les paires de nœuds du GC, nous dessinons des arêtes dans le GC. Ces arêtes représentent des portions communes entre le graphe partiel et le graphe réel. Il faut maintenant vérifier si le graphe partiel est entièrement présent dans le graphe réel. Cette vérification fait l’objet de la troisième étape.
Troisième étape
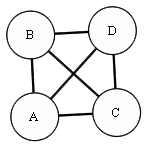
Schéma d’une clique de taille 4.
Pour vérifier que le graphe partiel est entièrement présent dans le graphe réel, il faut vérifier que tous les chemins reliant toutes les paires de nœuds du graphe partiel sont également présents dans le graphe réel. Cela revient à rechercher une clique de la taille du graphe partiel dans le graphe de compatibilité. Une clique est un ensemble de nœuds entièrement connectés les uns aux autres, où toutes les arêtes possibles entre ces nœuds existent. Par exemple, trois nœuds sont dans une clique si les trois arêtes possibles entre ces nœuds sont présentes dans le graphe (ainsi, l’eurypamide B est une clique, alors que le graphe partiel n’en est pas une). Pour quatre nœuds, la clique est constituée de six arêtes formant toutes les paires possibles entre ces nœuds.
Pour trouver une clique dans le graphe de compatibilité, il faut parcourir l’un après l’autre les nœuds du GC, regarder à quels nœuds ils sont reliés, puis vérifier que ces nœuds sont tous reliés entre eux. Plus le GC est grand, plus cette recherche peut prendre du temps. Le plus long est de rechercher une clique qui n’existe pas (lorsque le graphe partiel n’est pas présent dans le graphe réel) car il faut explorer tout le GC, qui peut être grand.
Heureusement, des astuces permettent d’arrêter la recherche de la clique avant d’avoir parcouru tout le GC. La première astuce utilise le fait que tous les nœuds du graphe partiel doivent être présents dans le graphe réel. Ainsi, il suffit de vérifier si un des nœuds du GC impliquant un seul et unique nœud du graphe partiel participe à une clique. Si ce n’est pas le cas, nous savons que le graphe partiel n’est pas présent dans le graphe réel et la recherche peut s’arrêter. Cependant, le parcours de tous les nœuds pouvant participer à la clique peut être long, car les graphes partiels peuvent être grands ou contenir beaucoup de positions incertaines. Dans ce cas, une deuxième astuce accélère encore le temps de réponse. Il s’agit de commencer la recherche de clique par le nœud du graphe partiel qui possède le plus grand nombre d’arêtes. En effet, il est plus probable que, s’il y a une différence entre le graphe partiel et le graphe réel, elle soit présente dans les arêtes partant de ce nœud. Si une telle différence est constatée, il ne sera pas nécessaire de parcourir le graphe en profondeur.
Par exemple, nous choisissons de commencer par le nœud « Thr » du graphe partiel, car c’est celui qui a le plus d’arêtes. De plus, il n’est associé qu’à un seul nœud de la didemnine N pour former le nœud « Thr, Thr » du graphe de compatibilité. Nous allons passer en revue quelques-uns des nœuds auxquels il est lié.
- Il est lié au nœud « X, Tyr », mais ce dernier n’est lié à aucun autre nœud. Nous obtenons une clique de taille 2 qui ne contient donc pas le graphe partiel complet, il faut poursuivre la recherche.
- Il est lié au nœud « X, Ist ». Ce dernier est également lié au nœud « Tyr, Tyr » qui est lui-même lié au nœud « Thr, Thr ». Nous avons bien trouvé une clique de taille 3, qui prouve que le graphe partiel est présent dans la didemnine N. La recherche peut s’arrêter. Cette clique représente une occurrence possible du graphe partiel, à savoir le triplet « Ist – Thr – Tyr ».
Une autre clique de taille 3 se cache dans le graphe de compatibilité, saurez-vous la trouver ? Cliquez sur le graphe pour afficher la réponse.
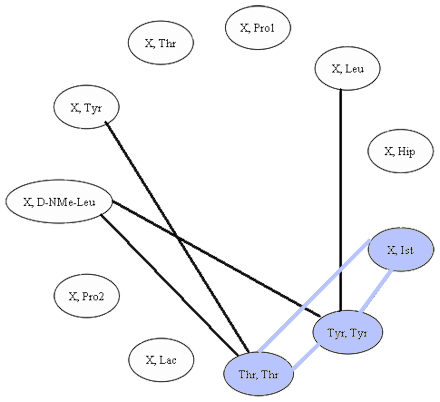
Clique de taille 3 trouvée dans le graphe de compatibilité.
La recherche de la présence d’un graphe partiel dans un graphe réel est à présent terminée. Si toutes les étapes ont été franchies avec succès, le programme affiche le peptide testé dans la liste des résultats. Si l’une des étapes renvoie une réponse négative, cela signifie que le peptide ne contient pas le graphe partiel. L’algorithme s’arrête et passe au graphe réel suivant.
Conclusion
La conception de la base de données Norine et de l’algorithme présenté ici est le fruit d’une collaboration étroite entre des bio-informaticiens de l’équipe Sequoia du centre de recherche INRIA Lille-Nord Europe et des biologistes du laboratoire ProBioGEM de l’Université de Lille 1.
Les spécificités des graphes représentant les peptides non-ribosomiques— et de l’imagination — nous ont permis de concevoir un algorithme efficace pour rechercher un graphe partiel au sein d’un ensemble de graphes. Les temps de calcul sur la base de données Norine sont de l’ordre de quelques centaines de millisecondes, au plus quelques milliers.
L’informatique répond aux besoins des scientifiques, qu’ils soient biologistes ou encore chimistes. Norine offre la possibilité de trouver des informations de qualité sur plus de mille peptides non-ribosomiques. Ainsi, la recherche d’informations noyées dans des milliers d’articles scientifiques n’est plus nécessaire. Il suffit d’interroger Norine. De plus, la possibilité de faire des recherches soit par mots-clés (par exemple le nom du peptide ou celui du micro-organisme qui le produit), soit directement parmi les structures des peptides, facilite l’étude des peptides.
La recherche dans ce domaine se poursuit, afin de proposer de nouveaux programmes qui vont aider les chercheurs à étudier ces molécules. Un succès pour Norine serait d’aider à la découverte de nouveaux médicaments ou d’autres produits naturels qui pourraient être utilisés à grande échelle. Par exemple, certains peptides non-ribosomiques ont la capacité de remplacer les pesticides chimiques utilisés pour protéger les plantes.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Maude Pupin