Du chaos dans les neurones
Au cours de l’histoire, le cerveau a été comparé à un moteur, à une horloge, un automate, un ordinateur, une « machine » inactive en l’absence d’informations à traiter, et s’enclenchant à l’arrivée d’une information, etc. En réalité, il est surtout constitué de neurones communiquant notamment au moyen d’impulsions électriques. L’évolution dans le temps de ces impulsions forme un code complexe, support du traitement de l’information.

Image : Delphine Bailly.
Dans le cerveau, le hasard se manifeste à tous les niveaux. Ainsi, deux canaux ioniques du même type présents sur une même synapse, peuvent laisser passer ou non les ions qu’ils contrôlent (a). De même, deux vésicules synaptiques transportant les mêmes molécules, des neurotransmetteurs, et paraissant dans des états identiques ne réagissent pas nécessairement de la même façon au même instant : l’une peut libérer son contenu dans la synapse, l’autre non (b). De même, deux neurones du même type et recevant les mêmes stimulus, n’émettent pas toujours les mêmes trains d’impulsions électriques (c). En outre, un troisième neurone, toujours du même type, peut voir certaines de ses synapses s’affaiblir, tandis que les synapses de deux autres neurones se renforcent (d). Ainsi, diverses sources de hasard expliquent pourquoi les décharges neuronales semblent aléatoires (e). Pourtant, dans le cerveau, si le hasard règne à l’échelle microscopique, le fonctionnement devient plus déterministe à grande échelle.
Les méthodes d’exploration du cerveau sont variées et donnent des informations complémentaires en termes de résolution spatiale et d’échelle de temps. L’électrophysiologie permet d’enregistrer l’activité d’un seul neurone (ou même d’une partie du neurone) ou d’une population de quelques neurones proches les uns des autres. Les techniques d’imagerie révèlent l’activité des populations de neurones situés dans une même zone. L’imagerie par résonance magnétique fonctionnelle (IRMf) concerne plusieurs centaines de milliers, voire quelques millions de neurones ; l’électroencéphalographie (EEG) et la magnétoencéphalographie (MEG) représentent l’activité de plusieurs centaines de millions de neurones.
Les variables analysées sont soit une activité électrique (dans le cas de l’EEG), soit un champ magnétique (MEG), soit d’autres signaux liés à la physiologie des neurones (IRMf). L’analyse de ces signaux par des algorithmes de traitement adaptés met en évidence des comportements divers dont certains sont chaotiques.
Aucune des méthodes ne fournit simultanément une bonne résolution spatiale et une bonne résolution temporelle. Certaines méthodes telles l’EEG et la MEG présentent des échelles de temps courtes (les signaux sont enregistrés en quelques millisecondes). La tomographie par émission de positons, au contraire, exige des durées notablement plus longues (l’IRMf aussi). En revanche, la résolution spatiale permise par l’EEG est celle d’une aire cérébrale, c’est-à-dire quelques centimètres. La microscopie, quant à elle, permet de visualiser des détails de l’ordre du micromètre. La méthode révélant avec précision l’évolution dans le temps d’une activité cérébrale locale reste à mettre au point.
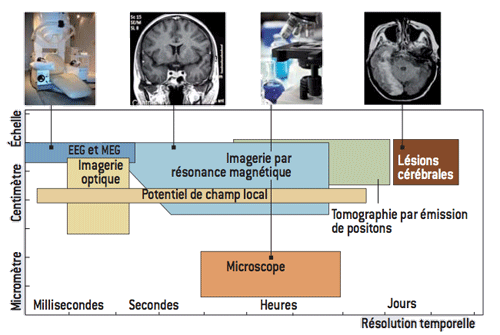
Les méthodes d’exploration du cerveau couvrent des échelles de temps différentes et présentent des résolutions allant de quelques micromètres (permettant de visualiser des synapses) à plusieurs centimètres (pour les aires cérébrales). Leur résolution temporelle varie de quelques millisecondes à quelques heures.
La neurobiologie dispose d’outils pour enregistrer la dynamique de cette activité électrique, à diverses échelles spatiales et temporelles. Petit à petit, on a découvert que, quelle que soit l’échelle à laquelle on l’observe, l’activité cérébrale évolue dans le temps et selon sa localisation dans le cerveau. Qui plus est, les dynamiques spatiales et temporelles des activités électriques enregistrées sont très irrégulières, et le cerveau est capable de passer d’un type d’activité électrique à un autre, très différent. Ces dynamiques complexes et leurs changements seraient associés au traitement de l’information par le cerveau.
Longtemps, on a pensé que l’activité cérébrale était nulle en l’absence de stimulus externe. Or il n’en est rien, puisqu’elle persiste même en l’absence d’« entrée » sensorielle. Imaginons que l’on jette un caillou dans une mare, puis un autre et encore un autre, etc. Les ondes circulaires créées par chaque caillou interagissent avec les précédentes. Il en résulte un motif spatial et temporel dépendant des interactions préexistantes et des nouvelles.
De même, lorsqu’une information nouvelle arrive dans le cerveau, elle modifie la dynamique de fond préexistante, et c’est sans doute cette interaction d’un stimulus et de cette dynamique qui permet au cerveau de répondre au stimulus de façon adaptée et reproductible. Cette conception est fondée sur des dynamiques spatio-temporelles complexes, dont nous allons discuter l’origine et la façon dont elles peuvent être utilisées par le cerveau pour traiter l’information. Nous examinerons d’abord quelques sources possibles de hasard : hasard au niveau des molécules, des cellules, des réseaux. Et pourtant, de ce désordre, naît un ordre à grande échelle, ou du moins un fonctionnement dynamique cohérent et reproductible.
Aléas à tous les niveaux
Quelles sont les causes possibles des dynamiques complexes observées expérimentalement ? À l’échelle moléculaire, les neurones émettent des impulsions électriques grâce à des protéines insérées dans leur membrane externe – des canaux ioniques –, qui peuvent être ouvertes, et laisser passer des ions, ou fermées, et empêcher ce passage.
Or l’état des canaux fluctue de façon aléatoire dans le temps, la probabilité d’ouverture et de fermeture dépendant notamment du potentiel de membrane, c’est-à-dire de la différence de potentiel de part et d’autre de la membrane (ou schématiquement de la différence des concentrations ioniques). Cette propriété explique l’émission d’impulsions électriques par les neurones. Notons que la forme des impulsions produites par ce mécanisme aléatoire est néanmoins remarquablement constante.
Comme c’est le cas pour tous les types de cellules, le comportement des neurones résulte des réactions biochimiques et des régulations génétiques intracellulaires. Or les dynamiques temporelles de ces réactions ou voies de régulation ont une composante aléatoire, ce qui a aussi des conséquences importantes sur le comportement électrique des neurones.
La transmission des impulsions électriques entre neurones est assurée par les neurotransmetteurs présents dans les zones de contact entre deux neurones, les synapses. Or la quantité de neurotransmetteurs libérés à chaque événement de transmission est très variable, de sorte que l’impulsion émise par un neurone en réponse à un autre a elle aussi une importante composante aléatoire. À l’échelle du neurone, la diversité des types de neurones et de leurs réponses à un même stimulus est considérable. D’une part, le nombre de sous-types de neurones dans le cortex est grand (sans doute des dizaines), et ils ont des comportements différents. D’autre part, des études expérimentales ont montré que la réponse d’un neurone à certains stimulus peut être très variable. Enfin, des études théoriques indiquent que le comportement électrique d’un neurone, même isolé des autres, peut présenter une dynamique chaotique.
Et ce n’est pas tout ! Non seulement les populations de neurones sont nombreuses, mais chaque neurone est connecté à d’innombrables neurones. Une cellule pyramidale du cortex, par exemple, est connectée à environ 10 000 autres neurones et reçoit de l’ordre de 70 000 impulsions électriques élémentaires plus ou moins indépendantes chaque seconde. Ce bombardement a un aspect aléatoire et engendre un « bruit synaptique », une activité de fond intense et irrégulière qui influe sur la façon dont les neurones réagissent à un stimulus.
Enfin, le réseau des connexions entre neurones a lui-même une structure partiellement aléatoire, qui engendre dans certains cas des comportements chaotiques. De surcroît, les connexions entre neurones sont dynamiques : l’influence d’un neurone sur un autre varie dans le temps. Ce phénomène, dit de plasticité synaptique, est en grande partie responsable des changements de comportements dynamiques des réseaux de neurones cérébraux (nous y reviendrons).
Distinguer le bruit du chaos
Ainsi, le fonctionnement du cerveau, de l’échelle moléculaire à l’échelle des réseaux de neurones, constitués de millions de cellules, est soumis à de multiples sources de complexité dynamique se manifestant sous forme de bruit ou de chaos. En quoi le bruit se distingue-t-il du chaos ? D’un point de vue expérimental, le bruit est une composante aléatoire qui se superpose à la partie déterministe d’un signal. Mathématiquement, le bruit est souvent représenté par une suite de variables aléatoires indépendantes. Et dans un système bruité, la connaissance des conditions initiales ne permet pas de connaître l’évolution future du système.
Dans un système chaotique déterministe, la connaissance des conditions initiales autorise en théorie à déterminer l’évolution du système à long terme. En revanche, pour que l’on puisse prédire cette évolution, il faudrait connaître l’état initial avec une précision infinie… Ce qui n’est évidemment pas possible. Or la plus petite erreur sur l’état initial engendre, à long terme, un comportement imprévisible. Ainsi, les systèmes chaotiques sont soumis à l’aléa résultant de la connaissance imparfaite des conditions initiales. Dès lors, pour savoir si un signal représente une dynamique chaotique, on doit l’analyser au moyen d’algorithmes de traitement adaptés.
En outre, on sait montrer mathématiquement qu’un système est chaotique en extrapolant son évolution temporelle sur des temps infinis. Le système est chaotique s’il évolue vers un état caractérisé par ce que l’on nomme un attracteur étrange. Un attracteur est une région de l’espace des phases vers laquelle convergent toutes les trajectoires des points associés au système étudié (l’espace des phases permet de représenter les variables indépendantes d’un système en fonction du temps). Il existe des attracteurs dits étranges : dans l’espace des phases, à proximité d’un attracteur étrange, deux trajectoires initialement très proches s’écartent rapidement.
En revanche, les systèmes chaotiques présentent, comme les systèmes bruités, une grande régularité statistique. Ainsi, les moyennes réalisées au fil du temps des quantités mesurables ne sont pas sensibles aux conditions initiales et évoluent de façon très régulière. C’est, par exemple, le cas d’un gaz, dont le comportement est décrit par des grandeurs telles que pression, volume, température, qui sont déterministes et constantes à l’équilibre, bien que la dynamique des molécules qui constituent ce gaz soit aléatoire. Cette régularité statistique est une clé d’un fonctionnement efficace du cerveau.
Comment mettre en évidence le chaos cérébral ?
Lors d’une expérience in vivo, aucun système ne peut être maintenu indéfiniment (ni même quelques instants) dans le même état. Dès lors, comment montre-t-on que le cerveau a, aux différentes échelles évoquées, un comportement chaotique ? Les études expérimentales portant sur des neurones isolés (voire sur une partie seulement d’un neurone) révèlent, dans certains cas, une dynamique chaotique. Qui plus est, John Guckenheimer et Ricardo Oliva, de l’Université Cornell, par exemple, ont montré que les équations les plus précises dont on dispose aujourd’hui pour décrire l’activité d’un neurone isolé (les équations de Hodgkin-Huxley) ont parfois un comportement chaotique.
Par ailleurs, les mathématiciens travaillent aussi sur des réseaux de neurones formels. Ce sont des modèles inspirés du fonctionnement des neurones, où chaque élément est relié à des éléments qui le précèdent (l’équivalent des neurones présynaptiques) et à un élément qui le suit (le neurone post-synaptique), la force de la connexion synaptique pouvant varier. On a mis en évidence du chaos dans de tels réseaux.
Le comportement d’un modèle de réseau de neurones est régi par des équations qui décrivent comment les neurones produisent des impulsions électriques et comment ces dernières se transmettent de neurone en neurone via les synapses. En s’inspirant de ces équations et, en général, en les simplifiant, on peut définir un modèle de réseau de neurones simplifié (ou formel) qui contient un certain nombre de caractéristiques d’un réseau biologique, sans pour autant chercher à reproduire entièrement la réalité. Par exemple, on peut considérer que les neurones transmettent des impulsions électriques, sans pour autant vouloir décrire toute la machinerie biologique qui permet aux neurones de les produire. On définit ainsi un système formel que l’on peut étudier mathématiquement, programmer sur un ordinateur, ou intégrer dans un circuit électronique.
On peut ainsi postuler qu’un « neurone » est caractérisé par « sa fonction de réponse » qui décrit comment il convertit les impulsions provenant des neurones présynaptiques en un train d’impulsions postsynaptiques. Cette fonction peut varier d’un neurone à l’autre en fonction de paramètres ajustables. De même, les synapses sont définies par un certain nombre de caractéristiques, telles que leur « poids » qui reflète l’intensité du potentiel postsynaptique qu’elles émettent (ou la force de la connexion). Ces poids peuvent évoluer au cours du temps, ce qui est une façon d’étudier la plasticité d’un réseau de neurones artificiels.
La façon dont l’ensemble des neurones et de leurs synapses évolue au cours du temps dépend des spécificités des neurones et des synapses, ainsi que des poids des synapses (ce que l’on peut représenter sous forme d’un graphe synaptique).
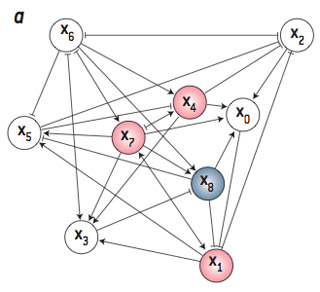
Cette évolution peut être étudiée mathématiquement ou simulée sur un ordinateur. On sait par exemple montrer que pour des formes assez générales de réponses neuronales et de graphes synaptiques (certains graphes aléatoires notamment), l’évolution est chaotique (voir la figure ci-dessous).
Prenons un exemple : la réponse d’un neurone est caractérisée par une variable indiquant la fréquence d’émission des potentiels d’action. On fait évoluer un paramètre g, tel que la réponse du neurone à un stimulus d’entrée n’est pas linéaire. En augmentant g, on amorce ce qu’on nomme une transition vers le chaos par quasi périodicité. On passe d’un état stable dans lequel les neurones émettent des impulsions électriques avec une fréquence constante, à un état où cette fréquence varie périodiquement, puis de façon quasi périodique (deux fréquences sont en concurrence). Ensuite, la dynamique des neurones devient chaotique. On caractérise l’évolution temporelle du réseau par la moyenne, à l’instant t, de la fréquence de décharge de tous les neurones.
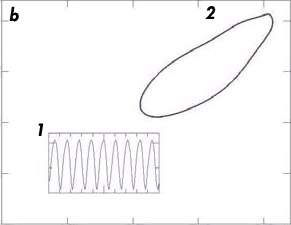
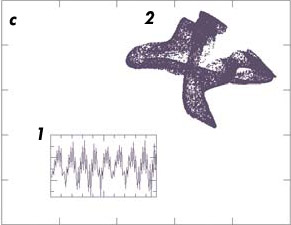
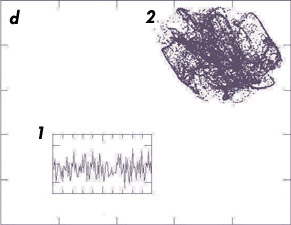
Images : Hugues Berry et Bruno Cessac.
Un exemple de réseau de neurones formel (a). Les neurones sont représentés par des cercles et les liaisons synaptiques par des flèches. Les couleurs symbolisent des types de neurones aux propriétés distinctes. Les synapses sont soit excitatrices (trait terminé par une pointe de flèche), soit inhibitrices (trait terminé par un T). Un tel réseau de neurones peut présenter divers comportements : un comportement périodique (b), un comportement quasi périodique (c) et, dans certaines conditions, un comportement chaotique (d), caractérisé par un attracteur étrange. De tels réseaux formels permettent de simuler de façon simplifiée le comportement de neurones réels. On a indiqué l’activité moyenne du réseau en fonction du temps (b1, c1 et d1). Les autres figures (b2, c2 et d2) représentent l’attracteur (en abscisse, l’activité moyenne au temps t et, en ordonnée, cette activité moyenne au temps (t+1)).
De très nombreuses études ont tenté de caractériser la dynamique des réseaux de neurones in vivo à une échelle plus globale, en particulier dans le signal fourni par les enregistrements d’électroencéphalographie. Au début des années 1980, l’étude des électroencéphalogrammes d’êtres humains durant l’éveil ou le sommeil peu profond a révélé la présence de chaos déterministe.
Des travaux datant du milieu des années 1980 ont suggéré la présence de chaos déterministe dans les signaux d’électroencéphalographie chez l’homme. Ces résultats ont montré que les signaux enregistrés lors des phases de sommeil profond présentent une structure chaotique qui diffère des structures mises en évidence durant les états de veille ou de sommeil peu profond.
De surcroît, il semble que la dimension des attracteurs étranges mis en évidence soit modifiée par certaines pathologies. En effet, durant les crises d’épilepsie ou encore lors du stade terminal de la maladie de Creutzfeldt-Jakob, les caractéristiques des attracteurs observés sont anormales. Ces observations pourraient être utiles à des fins diagnostiques.
Ainsi, chez les personnes épileptiques, l’électroencéphalogramme présente des modifications notables quelques minutes avant la survenue des crises. Certains chercheurs développent des méthodes capables de quantifier ces modifications en temps réel et de caractériser l’attracteur isolé du signal électroencéphalographique. Même si ces études se heurtent à de nombreuses difficultés, elles représentent un espoir, celui de prévoir automatiquement les crises d’épilepsie un peu avant qu’elles ne surviennent, afin, par exemple, d’administrer des médicaments pour les éviter.
De même, Walter Freeman, à l’Université de Berkeley, a proposé une hypothèse pour expliquer la dynamique des mécanismes de reconnaissance des odeurs dans le bulbe olfactif. Dans son modèle, la reconnaissance d’une odeur particulière se matérialise par un changement drastique : on passe brusquement d’un attracteur étrange à un autre attracteur de caractéristiques différentes et spécifiques de l’odeur.
Dès 1985, Walter Freeman et ses collègues, de l’Université de Berkeley, se sont intéressés au processus de reconnaissance d’odeurs dans le bulbe olfactif du lapin. En se fondant sur leurs observations, ils ont proposé un mécanisme où la dynamique des signaux observés est chaotique et où la reconnaissance d’une odeur particulière se matérialise par un changement drastique de dynamique que l’on nomme bifurcation : on passe d’un attracteur étrange à un attracteur d’un autre type, spécifique de l’odeur reconnue. Dans ce modèle, on associe à chaque odeur un attracteur, et c’est l’identification de cet attracteur qui permet la reconnaissance de l’odeur.
Au-delà des questions pratiques et conceptuelles qu’il soulève, ce modèle ouvre des perspectives intéressantes. Et s’il apparaît difficile de le valider sur des systèmes biologiques, il est possible d’essayer de le mettre en évidence dans des modèles mathématiques simplifiés de réseaux de neurones.
Il est assez facile de produire des modèles de réseaux de neurones dont la dynamique est chaotique. Dans un modèle que nous avons étudié, nous avons ainsi montré que si la structure du réseau synaptique est aléatoire, l’augmentation d’un paramètre correspondant à la réactivité des neurones entraîne une transition vers le chaos. L’attracteur est stable en ce sens qu’il se maintient si l’on soumet le réseau de neurones à des entrées de faible amplitude. Dans ce régime, les neurones ont un comportement chaotique quelle que soit l’entrée (de faible amplitude) : l’attracteur étrange n’est pas détruit par de petites perturbations. Mais les entrées sont si faibles qu’elles sont sans effet sur la dynamique neuronale collective.
C’est là qu’intervient la propriété de plasticité des réseaux neuronaux. Quel est l’effet d’un mécanisme de plasticité sur notre réseau ? La plasticité est la clé des mécanismes d’apprentissage, notamment. Nous avons donc présenté plusieurs fois les mêmes entrées au réseau de neurones et observé l’évolution des poids synaptiques et du comportement du réseau.
Nous avons tout d’abord observé que la plasticité réduit la complexité de la dynamique, alors que le réseau synaptique se structure. Dans les exemples que nous avons traités, nous avons observé, en présence de plasticité synaptique, une phase où la dynamique des neurones change de façon drastique lors de la présentation d’un stimulus. L’effet constaté ne se manifeste pas avant la phase d’adaptation synaptique : c’est une propriété acquise. Il se produit seulement pour des stimulus semblables à celui qui a été appris : c’est une propriété robuste. Il ne se produit pas pour des stimulus très différents : c’est une propriété sélective.
Ce comportement acquis s’apparente à celui que W. Freeman avait mis en évidence lors de l’apprentissage d’une odeur. Il est vraisemblable que d’autres mécanismes de plasticité sont à l’œuvre, qui permettraient de maintenir le réseau à la frontière du chaos.
Enfin, on a montré, in vitro, que des neurones isolés de calamar géant ou des petits réseaux isolés de cochon d’inde ou de certains crustacés présentent une dynamique chaotique. Les preuves de chaos dans les dynamiques enregistrées in vivo sont rares, car le système évolue sans cesse au gré des informations internes et externes qu’il reçoit. Pourtant, Henri Korn et Philippe Faure, de l’Institut Pasteur, à Paris, en ont confirmé l’existence en étudiant l’activité synaptique de neurones de poissons.
Les signaux d’électroencéphalographie semblent de prime abord totalement aléatoires. Pourtant, en traitant ces signaux et en éliminant le bruit, les mathématiciens font apparaître un ordre.
Toutefois, les enregistrements étudiés présentent une part importante de bruit et sont de courte durée. Dans ces conditions, il est difficile d’être certain que les activités enregistrées indiquent vraiment l’existence d’un chaos déterministe. Par ailleurs, les traitements mathématiques que l’on fait subir à ces signaux sont ajustés, avec, à nouveau, un risque de voir du chaos là où il n’est pas. Les indications de dynamique chaotique dans les électroencéphalogrammes doivent donc être considérées avec beaucoup de prudence. Néanmoins, des études récentes, notamment celles d’Alain Destexhe et Sami El Boustani, du Laboratoire Unité de neurosciences intégratives et computationnelles, UNIC, à Gif-sur-Yvette, ont confirmé la présence d’un chaos déterministe de faible dimension durant le sommeil.
Si l’on admet que l’activité cérébrale est chaotique et que ce type de hasard règne en maître, comment concilier chaos et traitement pertinent des informations par le cerveau ? Autrement dit, comment un système sensible aux conditions initiales peut-il traiter de l’information de façon fiable et reproductible ?
Supposons qu’on présente un objet à un sujet à deux instants successifs en lui demandant de le nommer à chaque fois. L’image de cet objet est traitée par la rétine, puis par le cortex visuel, puis par les centres de la parole. Le sujet nomme deux fois le même objet bien que l’état interne de son système de traitement soit différent aux deux instants. Or on sait que dans un système chaotique, par essence sensible aux conditions initiales, deux états différents évoluent différemment, ce qui doit rendre très variable – donc non reproductible – l’activité neuronale. Comment une telle variabilité peut-elle être compatible avec la reproductibilité de la réponse ?
Chaos local, mais ordre statistique global
Il faut d’abord noter que les neurones ne traitent pas à proprement parler d’« information ». Il serait plus exact de dire qu’ils reçoivent des impulsions électriques issues d’autres neurones auxquels ils sont connectés, que ces signaux les activent ou les inhibent, et que la conjonction de ces influences produit (ou non) une réponse neuronale. Si réponse il y a, elle se manifeste par une suite d’impulsions électriques qui, à son tour, agit sur d’autres neurones, etc. Ce traitement est en fait une chaîne causale d’actions et de réactions qui implique, par exemple, des neurones de la rétine, puis du cortex visuel, puis d’autres aires cérébrales, avec, à chaque étape, des rétroactions importantes.
Par ailleurs, on constate effectivement que les signaux enregistrés lors d’expériences identiques réalisées dans des conditions identiques diffèrent. Par exemple, les trains d’impulsions émis par les cellules ganglionnaires de la rétine ne sont pas identiques, même si l’image présentée est identique. Cette variabilité est due en partie à tous les mécanismes générateurs de bruit ou de chaos, aux différentes échelles déjà évoquées. Mais, surtout, la rétine ne code pas l’information comme le ferait un ordinateur : elle n’émet pas une suite précise de potentiels d’action où chaque image serait associée à une suite particulière. Dès lors, quel système de traitement serait susceptible de concilier variabilité des trains d’impulsions électriques et fiabilité de la réponse ?
Si les réponses prises une à une sont peu reproductibles, on constate que les trains d’impulsions présentent une régularité statistique, c’est-à-dire, par exemple, que la probabilité qu’un neurone décharge, ou que deux neurones déchargent en même temps, est relativement constante d’un essai à l’autre. Cette régularité statistique serait une clé des propriétés de reproductibilité et de fiabilité des réseaux de neurones. Cela signifie que l’émission de deux trains d’impulsions ayant les mêmes caractéristiques statistiques aboutit à des réponses similaires dans la chaîne de traitement.
Par exemple, si un groupe de neurones reçoit un nombre croissant d’impulsions provenant de neurones situés en amont, les neurones adoptent un état d’excitation qui leur permet, à un instant donné, d’émettre de façon synchrone des signaux vers un groupe de neurones situés en aval, etc. La reproductibilité des réponses ne nécessite pas la reproductibilité stricte des trains d’impulsions, mais est compatible avec une dynamique chaotique qui combine variabilité au niveau de chaque neurone, et régularité statistique du groupe.
S’il est difficile de valider la présence de chaos dans le cerveau et de le rendre compatible avec son fonctionnement, il est possible de tester diverses hypothèses sur des modèles mathématiques s’inspirant de la dynamique neuronale, et qui tentent de répondre à la question : comment un système chaotique peut-il traiter de l’information, par exemple produire des réponses adéquates à des signaux particuliers ?
Plusieurs équipes ont tenté d’utiliser des modèles mathématiques de réseaux de neurones chaotiques pour répondre à cette question. Nous avons ainsi proposé un modèle de réseaux de neurones chaotiques capable d’apprendre et de reconnaître des stimulus en utilisant la plasticité synaptique. Dans ce modèle, le système passe d’un état très désordonné en l’absence de stimulus à un état régulier (dont l’identification est simple et rapide) en présence d’un stimulus mémorisé. Le processus de plasticité conduit le réseau de neurones dynamique près d’un point de bifurcation, c’est-à-dire de changement brutal de comportement. Cette bifurcation se produit si l’on présente le stimulus appris ou un stimulus proche, mais pas si l’on présente un stimulus très différent.


Images : Hugues Berry et Bruno Cessac.
On peut représenter un réseau de neurones par son activité moyenne (sa fréquence de décharge moyenne) à un instant t (en abscisse) en fonction de son activité à l’instant (t 1) (en ordonnée). Dans cette représentation, un système périodique régulier donne (selon que la fréquence est rationnelle ou non) soit une courbe fermée, soit quelques points. Un système chaotique donne un nuage de points, où l’on peut discerner une structure (dans les cas de chaos de faible dimension). L’activité d’un réseau synaptique aléatoire sans plasticité synaptique change peu en l’absence (ci-dessus à gauche) ou en présence (à droite) d’un signal d’entrée.


En revanche, quand le réseau présente une plasticité synaptique, à la frontière du chaos, l’activité diffère radicalement en l’absence (à gauche) ou en présence (à droite) d’un signal d’entrée.
Dans cette animation on voit un exemple des effets induits par la plasticité hebbienne sur un réseau de neurones chaotiques. On a représenté l’attracteur de la dynamique au cours des époques successives d’apprentissage. On voit l’attracteur se structurer progressivement alors que la complexité de la dynamique se réduit. On passe ainsi d’un attracteur chaotique à une dynamique quasi périodique, puis périodique, pour finir par un régime stable où les neurones tirent à une fréquence constante.
Une soupe chaotique de neurones
D’autres types de structures de réseaux de neurones sont actuellement utilisés ; certains incluent une « soupe de neurones », constituée d’un grand nombre d’unités connectées de façon aléatoire et recevant les signaux d’entrée, et d’une couche d’unités qui traduit l’état interne de la soupe de neurones. Seule l’activité de la couche de traitement est contrainte, c’est-à-dire paramétrée par l’expérimentateur, alors que la soupe, dont la dynamique dépend du choix (aléatoire) des poids synaptiques et des stimulus qui peuvent être chaotiques, évolue librement.
Rappelons que dans un réseau de neurones, les poids synaptiques reflètent la force des synapses : certaines synapses sont dites renforcées, impliquant une connexion forte entre deux neurones – leur poids est alors élevé. Au contraire, quand une synapse est lâche, son poids synaptique est faible. La force des synapses évolue au fil du temps, certaines se renforçant, d’autres s’affaiblissant : c’est la plasticité synaptique. En imposant une règle de plasticité synaptique sur les connexions reliant la soupe de neurones et la couche de sortie, il est possible d’utiliser ces réseaux pour réaliser des tâches telles que la reconnaissance d’objets ou de signaux. D’après certaines équipes, ces structures seraient surtout pertinentes lorsque la dynamique de la soupe interne est à la frontière du chaos.
Abordons une autre propriété des réseaux de neurones chaotiques. On peut utiliser la grande régularité statistique des systèmes chaotiques pour transmettre des signaux identifiables. Des chercheurs, tel David Ruelle, un des pionniers de l’étude du chaos, ont généralisé à des systèmes chaotiques ce que l’on nomme en physique la théorie de la réponse linéaire. En appliquant cette théorie à un réseau de neurones chaotiques, l’un d’entre nous (B. Cessac) a ainsi montré en collaboration avec Jacques-Alexandre Sépulchre, de l’Institut non linéaire de Nice, qu’on peut transmettre un signal caché dans le bruit de fond chaotique. Ce signal ne peut être récupéré que par certains neurones du réseau. Cet exemple montre qu’on peut transmettre et extraire de l’information dans un réseau de neurones chaotiques. En revanche, nous ignorons si ce mécanisme est à l’œuvre dans les réseaux de neurones réels.
La dynamique cérébrale a lieu sur plusieurs échelles de temps et d’espace. Pour accéder à l’activité cérébrale à ces différentes échelles, il est nécessaire d’utiliser diverses techniques d’imagerie mesurant des grandeurs distinctes. La dynamique observée peut être très différente selon les échelles d’espace. Or ce n’est pas parce que la dynamique mesurée à une échelle donnée est irrégulière (chaotique) qu’elle est nécessairement irrégulière à une échelle supérieure. La raison en est un effet de moyenne. Si l’on mesure, par exemple, le champ électrique engendré par l’activité neuronale à l’échelle du millimètre, on enregistre en fait l’activité électrique cumulée de plusieurs milliers de neurones. Le champ mesuré est donc un champ moyen reflétant l’activité cumulée de cette population neuronale. Or, même si l’activité des neurones isolés est chaotique, la dynamique du champ moyen peut être régulière : le chaos au niveau neuronal n’implique pas le chaos à grande échelle.
Les leçons de la plasticité synaptique
Ainsi, le comportement dynamique du cerveau résulte d’une dynamique interne riche, complexe et à plusieurs échelles, et des stimulations dont la dynamique spatiale et temporelle est elle aussi complexe. À cela s’ajoute la plasticité synaptique, qui représente en quelque sorte une troisième dimension de la complexité de la dynamique du cerveau se combinant à la dynamique interne et aux entrées ; elle est responsable d’énormes modifications de cette dynamique. En outre, on pense aujourd’hui que cette plasticité (et les modifications de comportement qu’elle déclenche) est le support principal de l’apprentissage dans les systèmes neuronaux, leur conférant les capacités de reconnaissance, de généralisation et d’adaptation.
On distingue deux principaux types de plasticité synaptique. La plasticité dite à court terme s’exprime sur des durées comprises entre la milliseconde et quelques secondes. On regroupe sous ce terme les modifications du poids de la synapse dues principalement à la façon dont la machinerie de fabrication, libération et recyclage des neurotransmetteurs interagit avec la fréquence des impulsions émises par les neurones. Quant à la plasticité dite à long terme, elle s’exprime sur des durées de l’ordre de quelques heures à plusieurs jours, voire semaines. Elle implique plutôt des modifications de l’activité ou du nombre de protéines (c’est-à-dire de récepteurs des neurotransmetteurs) participant au fonctionnement de la synapse, voire du nombre de synapses actives entre deux neurones.
Il est difficile d’avoir une vue générique de l’effet de la plasticité synaptique sur la dynamique complexe des réseaux de neurones du cerveau et les fonctions qu’ils assument. En particulier, si cet effet est bien compris dans certains cas particuliers, nous n’avons toujours pas de théorie générique pour décrire ces effets sur la dynamique des réseaux.
Malgré de nombreux travaux de simulation, on ne dispose pas encore de théorie mathématique expliquant comment la plasticité synaptique modifie les régimes dynamiques complexes observés dans le cerveau. Notre propre travail est un pas dans cette direction. Au-delà des questions biologiques, le fait que des modèles mathématiques de réseaux de neurones puissent être chaotiques conduit à des applications surprenantes et ouvre de nouvelles perspectives. Il reste à développer les méthodes mathématiques et numériques adaptées pour mettre en relation ces perspectives théoriques avec des données biologiques !
- S. El Boustani et A. Destexhe, Brain dynamics at multiple scales : can one reconcile the apparent low-dimensional chaos of macroscopic variables with the seemingly stochastic behavior of single neurons ?, International Journal of Bifurcation and Chaos, à paraître.
- B. Siri et al., A mathematical analysis of the effects of hebbian learning rules on the dynamics and structure of discrete-time random recurrent neural networks, Neural Comp., vol. 20(12), pp. 2937-2966, 2008.
- B. Cessac et J.-A. Sepulchre, Transmitting a signal by amplitude modulation in a chaotic network, in Chaos, vol. 16(013104), 2006.
- J. Guckenheimer et R. Oliva, Chaos in the hodgkin-huxley model, Journal on Applied Dynamical Systems, vol. 1, p. 105, 2002.
- E. Daucé et al., Self-organization and dynamics reduction in recurrent networks: stimulus presentation and learning, Neural Networks, vol. 11, pp. 521-533, 1998.
- P. Faure et H. Korn, A nonrandom dynamic component in the synaptic noise of a central neuron, Proc. Natl. Acad. Sci. USA, vol. 94, pp. 6506-6511, 1997.
Une première version de ce document est parue dans la revue Pour la Science n°385, en novembre 2009.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Bruno Cessac
