Du rêve à la réalité des preuves

Il y a 100 ans paraissait le premier des trois tomes des Principia Mathematica d’Alfred Whitehead et Bertrand Russell. En s’appuyant sur les travaux de Gottlob Frege, Giuseppe Peano, Richard Dedekind et Georg Cantor, cet ouvrage montre comment réduire les mathématiques à la logique symbolique. L’ouvrage est l’un des plus importants de l’histoire des mathématiques, car il montre pour la première fois qu’un savoir scientifique peut être entièrement formalisé.
Avant le travail de Whitehead et Russell, écrire une démonstration mathématique était un exercice de nature littéraire où il fallait convaincre les lecteurs d’une affirmation abstraite. L’acceptation d’une preuve ou son refus résultait d’un consensus entre spécialistes conduisant le plus souvent à un accord unanime. Dans toutes les sciences, cette situation prévaut : il n’y a pas de procédure automatique et absolue de validation d’un résultat ou d’une théorie. On dispose de méthodes de contrôle, variées selon les disciplines, mais l’affaire reste humaine et dans certaines situations, les désaccords persistent longuement.
Avec les Principia, la formalisation des mathématiques fait basculer ces dernières dans une situation différente : vérifier si un résultat mathématique est juste peut être confié à un opérateur ignorant de ce dont traite la démonstration et qui se contentera de contrôler si les règles de manipulations symboliques des Principia, en nombre fini et fixées à l’avance, ont été respectées.
Cette formalisation est un immense progrès, puisque plus aucune controverse ne peut exister sur la validité d’une preuve écrite dans le langage des Principia. Si quelqu’un prétend qu’une preuve est fausse, l’opérateur ignorant trouvera l’erreur. Tout se passe comme pour un calcul arithmétique : aucune faute ne peut se dissimuler. Grâce à la formalisation, et comme l’avait imaginé Leibniz avec sa Characteristica universalis au XVIIe siècle, démontrer est devenu un simple calcul.
Un rêve !
Tout cela est très beau, mais c’est un rêve : la formalisation proposée par Whitehead et Russell est trop complexe pour être pratiquée dès qu’on aborde autre chose que des théorèmes élémentaires de logique ou d’arithmétique. Dans les Principia, les preuves formelles sont rarement écrites entièrement, les auteurs se contentant de montrer qu’elles existent et d’indiquer ce qu’il faudrait faire pour les écrire.
Avec les Principia, les mathématiques deviennent formalisables en principe, mais pas en réalité. S’en tenir au langage des Principia conduit à des preuves dont la longueur empêche leur écriture effective et donc le contrôle. Le formalisme des Principia n’est pas praticable et la garantie qu’aurait dû donner le formalisme ne fonctionne pas.
D’autres formalisations générales des mathématiques ont été proposées, dont celle de Bourbaki, le célèbre mathématicien français polycéphale. Sa proposition, qui date des années 1930, s’appuie sur la théorie des ensembles et le logicien Adrian Mathias en a révélé une propriété cocasse. Dans le formalisme de Bourbaki, la notation complète pour désigner le nombre « 1 » est une longue suite de symboles et Bourbaki indiquait que si l’on tentait de la déployer sans utiliser aucun raccourci, l’écriture complète du « 1 » comporterait quelques dizaines de milliers de symboles. A. Mathias a montré que la situation était pire et qu’écrire le nombre « 1 », en respectant à la lettre le formalisme de Bourbaki, nécessiterait 4 523 659 424 929 symboles, soit l’équivalent de quatre millions de livres de 400 pages.
L’informatique rend-elle tout simple ?
Les premiers formalismes complets proposés pour les mathématiques ne sont pas destinés aux mathématiciens terrestres ! Pourtant, l’informatique et un siècle de travail de la part des logiciens ont maintenant transformé le rêve en réalité. Le « en principe » qui était juxtaposé à « mathématiques formalisables » peut être enlevé.
L’informatique n’a pas peur des grandes quantités de données. La formalisation des Principia ou celle du traité de Bourbaki à l’aide des ordinateurs fonctionnerait-elle sans peine ?
Non. Les calculs informatiques ne peuvent tout affronter et la formidable puissance des ordinateurs ne dispense pas d’être intelligent. Nos machines sont de capacité limitée et ce n’est pas parce le progrès est rapide que l’on dispose d’une puissance infinie. Ainsi, on ne sait pas aujourd’hui ni trouver un nombre premier de plus de 13 millions de chiffres ni calculer un million de milliards de décimales de π, on en est seulement à dix mille milliards de décimales. Le formalisme des Principia ou du traité de Bourbaki est bien trop gourmand en puissance, même pour les plus puissants des ordinateurs ou des réseaux informatiques.
Attendre serait une solution, mais il n’est pas certain que les progrès technologiques ne butent pas sur une limite ultime : il est probable, au contraire, que la miniaturisation ne pourra aller en deçà de la taille des atomes. Le plus sage pour obtenir une formalisation pratique et réelle des mathématiques est donc de mener une double attaque : améliorer les formalismes en les simplifiant pour les rendre praticables et profiter des gains de puissance que la technologie nous offre. C’est ce que l’on a fait et l’heure du succès est maintenant arrivée.
Assistant de preuve
Le premier travail de formalisation des mathématiques fut le projet Automath conçu et développé aux Pays-Bas à partir de 1966 par Nicolaas de Bruijn. Il fut suivi par une série de projets dont les plus avancés sont, en Pologne le projet Mizar, en Grande-Bretagne et aux États-Unis le projet HOL-Isabelle et en France, le projet Coq.
L’idée est de mettre à la disposition du mathématicien un système informatique interactif et un formalisme de démonstration qui lui permettent d’élaborer une version formelle du résultat auquel il s’intéresse en dialoguant avec le logiciel. Le logiciel libère le mathématicien d’une partie du fastidieux travail d’écriture et opère les contrôles minutieux nécessaires à chaque étape de l’explicitation d’une démonstration formelle. Le logiciel stocke aussi les résultats démontrés formellement par d’autres mathématiciens lors de séances antérieures, et ces résultats sont utilisables pour des preuves nouvelles.
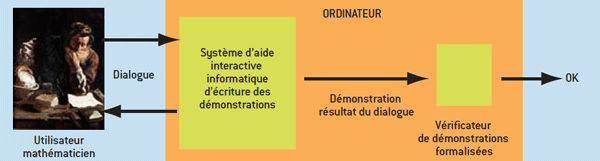
Un logiciel assistant de preuve est destiné à aider un mathématicien à écrire des démonstrations formelles lors de sessions de travail interactives. Pour ce faire, le mathématicien traducteur de la démonstration classique en démonstration formelle doit avoir une parfaite connaissance de la preuve, ce qui n’est pas facile dans le cas d’une démonstration complexe. De plus, la traduction est difficile et lente : une ou plusieurs pages par jour.
La partie du programme informatique qui gère les interactions est longue et délicate et, de ce fait, peut comporter des erreurs. C’est sans importance, car la preuve produite à l’issue du dialogue sera vérifiée par le cœur du système, qui lui seul doit être correct. Cette partie centrale est courte et vérifiée de façon indépendante par plusieurs spécialistes. On utilise parfois un autre logiciel assistant de preuve pour démontrer que ce cœur fonctionne correctement. La petite taille des parties centrales, et le soin particulier à les vérifier et à les prouver n’annulent pas le risque d’erreur finale (et donc la validation de preuves fausses), mais réduisent de plusieurs ordres de grandeur ce risque. Avec la formalisation des preuves, on améliore donc sensiblement la garantie de justesse de ce qui est démontré.
Pour mesurer le succès des logiciels assistants de preuve qui formalisent de vraies mathématiques, nous examinerons la liste des théorèmes centraux des mathématiques dont on a aujourd’hui réussi à produire une preuve formalisée qui en garantit de manière quasi absolue l’exactitude.
Imitant l’idée de la liste des 100 meilleures chansons, Nathan Kahn, mathématicien du Steven Institute of Technology, dans le New Jersey, a composé une liste des « 100 théorèmes mathématiques les plus importants ». Cette liste, subjective, a cependant été adoptée comme repère par les chercheurs qui mettent au point les logiciels de formalisation des mathématiques et elle permet d’en comparer les succès.
87 % des théorèmes
Au cours du temps, le nombre des théorèmes que l’on a formalisés dans la liste de Kahn augmente et, aujourd’hui, on en est à 87 sur les 100 de sa liste. Citons quelques-uns de ces théorèmes maintenant garantis par la machine.
- Irrationalité de la racine carrée de 2 : √2 n’est pas égal à un quotient de deux nombres entiers.
- Infinité des nombres premiers : la suite des nombres entiers n’ayant pas d’autres diviseurs que 1 et eux-mêmes est une suite infinie (2, 3, 5, 7, 11, 13, …).
- Impossibilité de la trisection d’un angle par une construction exacte menée avec seulement une règle et un compas.
- Théorème des quatre carrés de Lagrange : tout nombre entier s’écrit comme la somme de quatre carrés (par exemple 23 = 32 + 32 + 22 + 1).
- Formule de Leibniz : π/4= 1 – 1/3 + 1/5 – 1/7 + 1/9 – …
- Divergence de la série harmonique 1 + 1/2 + 1/3 + 1/4 + …
- Théorème fondamental de l’algèbre : un polynôme de degré n à coefficients complexes possède n racines.
- Théorème fondamental de l’analyse : la dérivée de l’intégrale, prise entre une constante a et x, de la fonction f, est égale à f (x).
- Transcendance de e : le nombre e = 2,182818284590… n’est racine d’aucun polynôme à coefficients entiers.
- Premier théorème d’incomplétude de Gödel : tout système formel non contradictoire pour l’arithmétique ou une théorie plus puissante laisse sans démonstration certains énoncés vrais.
- Théorème des nombres premiers par Hadamard et par de La Vallée-Poussin : la densité des nombres premiers autour de n est 1/log (n).
- Théorème des quatre couleurs : toute carte dessinée sur un plan peut être coloriée avec quatre couleurs de façon que deux pays voisins soient de couleurs différentes.
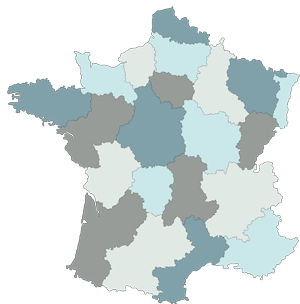
On peut colorier une carte, comme celle des régions de France, avec quatre couleurs seulement. Le « théorème des quatre couleurs » a été définitivement prouvé par un assistant de preuve, ce qui a mis fin à une controverse sur les premières démonstrations.
Ce dernier théorème est le plus difficile de tous ceux dont la démonstration a pu être contrôlée par la méthode de l’écriture complète d’une preuve formelle. La preuve formelle a été obtenue en 2004 par Georges Gonthier et Benjamin Werner avec le logiciel Coq développé au sein d’Inria (Institut national de recherche en informatique et en automatique).
Précisons que ce théorème avait été démontré en 1976 en utilisant une démonstration comportant deux parties. Une partie de la preuve était informelle, c’est-à-dire exposée dans un texte en langue naturelle (l’anglais) comme le sont toutes les preuves mathématiques publiées dans les journaux et livres mathématiques. Une autre partie de la démonstration était un calcul mené par ordinateur, calcul trop long pour qu’on puisse le réaliser sans machine. La preuve de 1976 n’était en rien formalisée et elle pouvait parfaitement comporter des erreurs, soit dans la partie informelle, soit dans la partie informatique si les programmes utilisés étaient incorrects ou que la machine avait commis des erreurs.
Le travail consistant à prouver le théorème des quatre couleurs de façon formelle n’était donc pas du tout réglé d’avance ni même rendu plus facile par l’utilisation d’ordinateurs pour une partie de la preuve de 1976. Cette utilisation était en fait seulement l’indice que l’on avait affaire à un résultat particulièrement compliqué.
Notons aussi que le logiciel Coq est souple et adaptable à de nombreux problèmes, et que José Grimm d’Inria a pu grâce à lui entreprendre de formaliser les Éléments de mathématique de Bourbaki. L’idée n’est pas de suivre exactement le formalisme décrit dans le traité – nous avons vu que ce n’était pas envisageable –, mais de concevoir un formalisme équivalent permettant d’exprimer tous les résultats que l’on y trouve en même temps qu’on formalise le détail des preuves. Aujourd’hui, une grande partie du livre I du traité de Bourbaki a été formalisée.
Des théorèmes encore trop complexes
Parmi les 13 résultats de la liste des 100 théorèmes qui restent trop difficiles à formaliser aujourd’hui, même en utilisant des assistants de preuve, citons en deux.
- La transcendance du nombre π. C’est l’affirmation que π n’est racine d’aucun polynôme à coefficients entiers (ce résultat montre que l’antique problème de la quadrature du cercle est insoluble). Le théorème a été démontré par Lindemann en 1882 et on peut dire qu’il est à la limite de ce que peuvent faire les assistants de preuve actuels. Il est probable qu’il sera rapidement prouvé de manière formelle.
- Le théorème de Fermat-Wiles. C’est l’affirmation, démontrée en 1993 par Andrew Wiles, qu’il n’existe pas de solutions à l’équation xn + yn = zn où x, y, z sont des entiers positifs et n un entier fixé supérieur à 2.
Sa preuve est extrêmement difficile. Elle avait été recherchée pendant 350 ans et elle n’est vraiment comprise que par quelques spécialistes. En produire une version formelle serait intéressant.
Même si les erreurs sont fréquentes, le fait qu’une démonstration soit faite et refaite par de nombreux mathématiciens assure qu’aucun résultat classique n’est faux. Jamais dans les parties centrales des mathématiques une erreur grave n’est restée longtemps cachée. Aussi le délicat, long et pénible travail de formalisation des mathématiques avec assistant informatique est-il vraiment utile ? La réponse est deux fois « oui ».
Vraiment utiles ?
Oui, la formalisation est utile, car certaines démonstrations récentes sont si longues que personne n’est entièrement persuadé de leur exactitude. C’est le cas du théorème de Thomas Hales qui résout la conjecture de Kepler concernant l’empilement optimal des sphères dans l’espace. Personne ne peut dire que la preuve de Hales a été contrôlée. Mener la vérification formelle d’une telle preuve n’est donc pas un luxe, mais une nécessité.
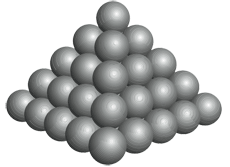
Le travail d’écriture de preuves formelles en utilisant les assistants de preuve informatiques est parfois considéré avec méfiance et scepticisme. L’idée est que, pour peu que les démonstrations mathématiques soient écrites avec suffisamment de soin et contrôlées par des experts humains, on élimine tout risque d’erreur. Cette idée n’est plus défendable depuis que Thomas Hales a proposé une démonstration (non formelle) de la conjecture de Kepler, jugée impossible à contrôler par les experts à qui on l’avait confiée.
Cette conjecture affirme que l’empilement de sphères le plus dense est celui utilisé pour les boulets de canon ou les oranges : un réseau triangulaire de boulets est créé sur le sol plat ; on pose dessus un autre réseau analogue en exploitant les creux du premier et de même un troisième réseau, etc.
La démonstration de Th. Hales a été publiée par le prestigieux Annals of Mathematics en 2005 avec la mise en garde que, du fait de la complexité de la démonstration et de l’utilisation pour certaines de ses parties de programmes informatiques, le comité d’experts chargé de l’examiner ne pouvait pas en garantir l’exactitude. Devant cette situation inédite, Th. Hales a entrepris le projet de produire une preuve formelle (et donc mécaniquement vérifiable) de son théorème. Son programme de travail, qui pourrait occuper son équipe pour une durée de dix années ou plus, avance régulièrement. Il a déjà donné lieu à deux doctorats de mathématiques et à la mise au point d’une preuve formelle d’un résultat à l’énoncé simple, mais dont la démonstration formelle posait des difficultés : le théorème de Jordan.
Celui-ci indique que lorsqu’on enlève les points d’une courbe plane continue et fermée qui ne se recoupe pas (une boucle), la partie du plan qui reste est composée de deux morceaux disjoints, chacun d’un seul tenant.
Mise à jour : le 10 août 2014, Th. Hales a annoncé que son projet avait abouti, la preuve formelle de son théorème est désormais disponible.
Les mathématiques donnent lieu à des démonstrations de plus en plus longues et difficiles et l’utilisation de preuves formalisées pourrait bien devenir routinière.
La situation est pire encore dans le cas du théorème de classification des groupes simples, dont la première démonstration a été annoncée en 1983. Elle s’étend sur des dizaines d’articles mathématiques écrits par plus d’une centaine de mathématiciens différents et couvre un total de plus de 10 000 pages. Un trou important y a été découvert, qu’un complément de 1 300 pages est venu combler dans les années 1990. La seconde version de cette démonstration est en cours d’élaboration et s’étendra sur environ 5 000 pages. Bien qu’impossible à envisager dans l’immédiat, il est clair que seule la mise au point d’une preuve formelle sera susceptible de rassurer définitivement les mathématiciens qui, comme Jean-Pierre Serre, doutent de l’exactitude de ce théorème « monstrueux ».
Oui, la formalisation des démonstrations mathématiques est utile, car elle sert à certifier des logiciels ou des puces informatiques ainsi d’ailleurs qu’à y repérer des erreurs. Les « assistants de preuve » utilisés pour la mise au point des preuves formelles sont des outils puissants exploités par l’industrie du logiciel pour les morceaux de programme dont on veut avoir la certitude qu’ils font correctement certaines tâches cruciales.

Ces logiciels, qui aident à produire des démonstrations formalisées de théorèmes, sont aussi utilisés pour démontrer que certains circuits de microprocesseurs, dont le Pentium 4, fonctionnent correctement. La démarche est prudente, car, en octobre 1994, Thomas Nicely, de l’Université de Lynchburg (États-Unis), a dévoilé un dysfonctionnement dans l’unité de calcul en virgule flottante du Pentium : il s’est rendu compte que certaines opérations du processeur renvoyaient une valeur erronée par excès.
Photo : Matthieu Riegler, Wikimedia Commons.
Aujourd’hui, assez peu de logiciels sont ainsi validés par la formalisation complète de la démonstration qu’ils font ce qu’on attend et rien d’autre, et de nombreuses autres méthodes de contrôle et de certification sont utilisées. Cependant, on a là, venue des mathématiques et de la logique, une technique quasi définitive permettant d’assurer l’absence de bogues dans les parties clefs d’un programme ou d’un microprocesseur. En 1993, la firme Intel avait mis en circulation une puce qui commettait des erreurs arithmétiques ennuyeuses ; elle utilise aujourd’hui la méthode des assistants de preuve pour éviter que cela ne se reproduise.

Avec des assistants de preuve, des erreurs auraient été évitées. Le 4 juin 1996, la fusée Ariane 5 explosait 40 secondes après son décollage. La catastrophe résultait d’une erreur de programmation.
Récemment dans un article du New York Times, Adi Shamir (le S du système de cryptage RSA) faisait remarquer que la présence d’une seule erreur dans une puce informatique largement utilisée mettrait en danger la sécurité de millions de machines ; elle rendrait peut-être manipulables frauduleusement toutes les transactions faussement sécurisées du commerce électronique.
Non seulement la présence d’erreurs dans les logiciels et les puces peut faire tomber la fusée Ariane, ce qui s’est produit le 4 juin 1996, mais elle peut aussi être à l’origine de problèmes économiques majeurs. Les difficultés qu’on a en mathématiques à garantir l’exactitude des longues démonstrations et les méthodes élaborées pour résoudre ce qui ne semblait devoir n’intéresser qu’une petite communauté de chercheurs se révèlent importantes pour tout le monde. C’est là un exemple nouveau et spectaculaire de l’utilité des théories abstraites, ici la logique mathématique.
Quelle certitude ?
Certains voient un paradoxe dans l’idée d’utiliser l’informatique pour contrôler des démonstrations mathématiques, car notre expérience des ordinateurs montre que loin d’être des outils fiables, ce sont des sources nouvelles et incontrôlables d’erreurs dont on ne comprend souvent pas l’origine : on redémarre sa machine et ça s’arrange (parfois…) sans que personne ne sache pourquoi. Comment, dès lors, croire que les preuves formelles par ordinateur sont plus sûres que les preuves informelles et humaines ?
La réponse est que les assistants de preuve reposent sur des noyaux logiciels, la partie qui mène le contrôle des preuves produites lors des séances de travail interactif, aussi petits que possible et que l’on contrôle minutieusement :
(a) En s’arrangeant pour que leur présentation soit la plus lisible et la plus simple possible, et en demandant ensuite à un nombre aussi grand que possible de spécialistes de relire ces programmes clefs.
(b) En testant ces noyaux logiciels sur de très nombreux exemples : si une erreur persistait, elle aurait très probablement des conséquences et aurait produit des effets visibles lors des essais.
(c) En démontrant formellement que ces noyaux logiciels sont corrects à l’aide de versions différentes du même noyau ou, mieux encore, avec d’autres assistants de preuve écrits par des groupes de chercheurs indépendants.
Bien sûr, on n’arrive pas à une certitude totale que le noyau de l’assistant de preuve est sans erreur, mais à une très faible probabilité qu’il en contienne. Tout le risque se concentre sur un petit nombre de lignes de programmes (moins de 500 dans le cas de l’assistant HOL) et sur lui seul. Au total, on a considérablement gagné en sûreté et sans doute réduit le risque d’erreur de plusieurs ordres de grandeur. De même que les théorèmes les plus anciens des mathématiques ayant été redémontrés (sans utiliser d’assistant de preuve) un grand nombre de fois ne contiennent certainement aucune erreur, les noyaux des assistants de preuve gagnent en fiabilité à mesure du temps. Toutes les autres preuves reposent sur eux, et l’on atteint donc une certitude de correction quasi absolue.
Les assistants de preuve ne seraient-ils pas susceptibles de changer notre façon de faire des mathématiques ? C’est l’idée du manifeste QED dont le nom vient de l’expression latine Quod Erat Demonstrandum (Ce qu’il fallait démontrer). Formulé en 1994 par des chercheurs qui ont souhaité rester anonymes, ce manifeste énonce l’objectif de mettre au point un assistant de preuve général pour toutes les mathématiques, de manière à garantir la totalité de tout ce qui se fait dans la discipline.
L’assistant de preuve envisagé serait à la fois puissant, fonctionnant avec un formalisme proche du langage qu’utilisent les mathématiciens, et évidemment serait aussi sûr que possible. Avec un tel assistant de preuve, on formaliserait toutes les mathématiques existantes et à chaque fois qu’un nouveau résultat serait proposé, le chercheur qui le soumettrait en donnerait une preuve formelle, ce qui dispenserait de le faire expertiser par d’autres chercheurs. La pratique de la recherche mathématique en serait transformée.

Dessin : Jean-Michel Thiriet
Aujourd’hui, cet assistant de preuve idéal n’existe pas. Les assistants de preuve actuels restent trop compliqués et les langages qu’ils utilisent souvent éloignés de celui pratiqué par les mathématiciens. Formaliser une preuve reste un énorme travail et il faut un ou plusieurs jours par page pour traduire une preuve classique d’un article mathématique en preuve formelle.
Tout cela fait que les chercheurs en mathématiques n’utilisent que très rarement les assistants de preuve disponibles et que la communication entre mathématiciens continue de fonctionner par échange de preuves informelles et sans processus de validation informatique. Le chemin menant à une nouvelle pratique des mathématiques n’est pas achevé et il n’est pas sûr qu’on atteindra l’idéal imaginé par le manifeste QED.
Toutefois, Henk Barendregt et Freek Wiedijk, deux spécialistes des preuves formelles, prédisent que le changement dans la recherche mathématique se produira dans la prochaine décennie.
Prouver ainsi tous les résultats ?
D’ici quelques années, les assistants de preuve seront probablement en mesure de prouver l’ensemble des résultats mathématiques classiques.
Aujourd’hui, des théorèmes très difficiles ont pu être validés par la méthode des preuves formelles. C’est le cas du théorème des nombres premiers de Jacques Hadamard et Charles de La Vallée-Poussin (qui précise la densité asymptotique des nombres premiers), dont deux démonstrations différentes ont été formalisées et validées.
Il n’en est pas de même pour des résultats plus avancés comme le grand théorème de Fermat, qui reste trop complexe pour les outils actuels. Mais F. Wiedijk et d’autres chercheurs du domaine considèrent que ce n’est qu’une question de moyens, et que même les plus difficiles des grands théorèmes sont maintenant à portée de main.
Mentionnons encore deux points. Il n’est pas question de laisser à la machine l’initiative de la recherche mathématique : sauf dans des cas exceptionnels ou à propos de problèmes se réduisant à du calcul, les méthodes de recherche automatique de preuves ne trouvent que des résultats faciles et ne peuvent donc pas se substituer au mathématicien humain, qui reste la clef des découvertes.
Les assistants de preuve permettent d’accroître la sûreté des démonstrations, mais la fonction d’une démonstration, en particulier dans l’enseignement, est aussi de faire comprendre ce qui se passe mathématiquement dans l’univers des objets abstraits. Or les preuves formelles, désagréables à lire, entravent la compréhension plus qu’elles ne l’aident. Même si les objectifs du manifeste QED sont un jour atteints, on continuera d’écrire des preuves informelles, car ce sont elles qui font passer les idées d’un cerveau de mathématicien à un autre.
Les démonstrations formelles sont peu lisibles et même souvent illisibles. Cela ne doit pas surprendre, car, sans qu’on ait toujours bien fait la distinction, les démonstrations mathématiques possèdent deux fonctions.
La première fonction d’une démonstration est de garantir que l’affirmation exprimée dans l’énoncé du théorème est exacte. C’est la fonction de certification. La seconde fonction est de permettre au mathématicien de percevoir et de comprendre pourquoi les choses sont comme le théorème l’énonce. C’est la fonction didactique. Lorsque les démonstrations ne sont pas trop compliquées, les deux fonctions peuvent être envisagées simultanément : le texte de la démonstration assure la validité de l’énoncé et, en même temps, il en explique les raisons profondes.
Lorsqu’on a affaire à des résultats vraiment difficiles, un double travail est nécessaire. La complexité dans le cas des mathématiques a donc pour conséquence la nécessité :
- d’une part, de mener un contrôle formel (par l’utilisation des assistants de preuve),
- d’autre part, de présenter un texte non formel illustré et largement commenté expliquant les idées mises en œuvre dans la démonstration.
C’est ce second texte qui permettra aux mathématiciens de saisir le sens du théorème… et d’imaginer le prochain théorème et la façon dont il faudra à son tour le démontrer.
- F. Wiedijk, Formalizing the « top 100» of mathematical theorems, 2011
- H. Geuvers, Proof assistants : History, ideas and future, Sadhana, vol. 34-1, pp. 3-25, février 2009
- G. Gonthier, The four-color theorem, Notices of the AMS, vol. 55, n° 11, pp. 1382-1393, 2008.
- Th. Hales, A proof of the Kepler conjecture, Annals of Mathematics, vol. 162, pp. 1065-1185, 2007.
- F. Wiedijk, Formal proof – Getting started, Notices of the AMS, vol. 55, n° 11, pp. 1408-1414, 2008.
- Th. Hales, Formal proof, Notices of the AMS, vol. 55, n° 11, pp. 1370-1380, 2008.
- F. Wiedijk, The QED manifesto revisited, Studies in Logic, Grammar and Rhetoric, vol. 10(23), pp. 121-133, 2007.
- F. Wiedijk (éd.), The Seventeen Provers of the World, Springer, 2006.
Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°402, en avril 2011.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).