Estimer les courants océaniques depuis l’espace

Contexte

L’océan n’est pas statique : au-delà des manifestations évidentes de la dynamique océanique que nous expérimentons tous, comme les vagues ou la marée, l’océan abrite une multitude de courants et autres perturbations dynamiques de ses propriétés — niveau de la mer, température, salinité. Ces différents types de mouvements sont complexes et pilotent, entre autres, le rôle climatique de l’océan.

La dynamique océanique peut être étudiée suivant plusieurs approches : mathématiquement, on décrit l’évolution des différentes variables caractérisant l’état de l’océan par un ensemble d’équations issues de la mécanique des fluides. Ces équations étant trop complexes pour en trouver une solution exacte, on recourt souvent à des simulations numériques pour trouver des solutions approchées. Enfin, on peut mesurer directement ce que sont les « valeurs » que prennent ces différentes variables, à l’aide de différents instruments de mesure, in situ via les campagnes océanographiques ou à distance à l’aide d’instruments de télédétection (satellites, radars…).

C’est aux observations par satellite, et à leur utilisation dans le but de mieux caractériser la circulation océanique, que nous nous intéressons dans cet article. Qu’observe-t-on ? Quelles informations peut-on en déduire ? Comment procède-t-on ?

Observations spatiales

Via le déploiement de satellites à partir des années 1970, la télédétection a révolutionné l’océanographie physique. La flotte actuelle de satellites en compte un peu plus d’une vingtaine. De manière générale, le principe de fonctionnement repose sur le traitement d’un signal électromagnétique reçu par les capteurs embarqués. Ce signal peut avoir été émis par un instrument à bord du satellite (télédétection active) ou directement par le milieu observé (l’eau, dans notre cas — télédétection passive). Inconvénient majeur : à la différence de l’atmosphère, le signal électromagnétique ne pénètre pas dans l’eau, et les satellites ne donnent donc accès qu’à une mesure à la surface de l’océan.

L’une des variables d’importance que l’on peut mesurer depuis les satellites est le niveau de la mer, dont les perturbations sont intrinsèquement liées aux courants. Depuis le début des années 1990, l’altimétrie satellitaire donne une information le long d’une trace à l’aplomb du satellite avec une précision de l’ordre du centimètre (en chaque point). Elle a ainsi constitué un apport majeur dans notre compréhension de la dynamique océanique sur les 30 dernières années.

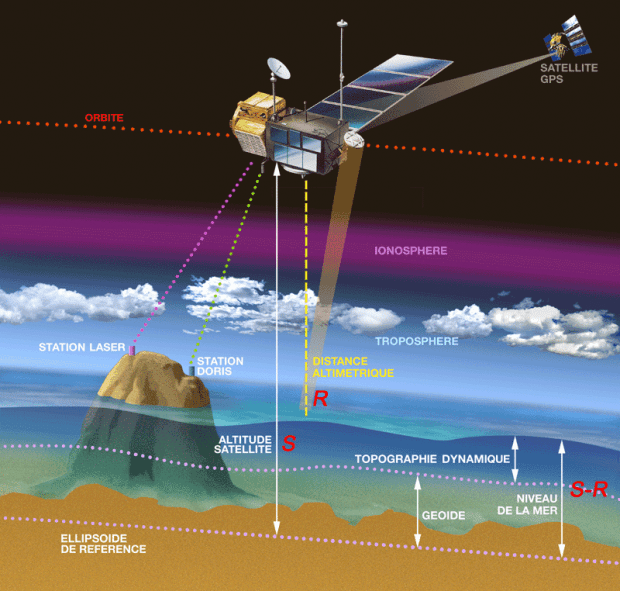
Figure 1 : Illustration de la mesure du niveau de la mer par satellite. Connaissant la position du satellite le long de son orbite ainsi que son altitude \(S\), et mesurant la distance entre le satellite et la surface de l’océan \(R\) (via le temps de propagation du signal électromagnétique), on en déduit le niveau de la mer \(R−S\). (Détail technique de moindre importance ici : le niveau de la mer « au repos » n’est pas exactement ellipsoïdale à cause des variations spatiales de la gravité associées aux reliefs sous-marins.)

Modèles et estimations

L’altimétrie satellitaire permet notamment de cartographier deux « classes » de mouvements océaniques d’importance primordiale :

1. Les grandes structures de courants et de tourbillons, que l’on peut cartographier aujourd’hui avec une résolution spatiale effective de l’ordre de 100 km ;
2. La marée, qui est associée à des perturbations du niveau de la mer de l’ordre du mètre en pleine mer, se propageant — tournant — dans les bassins océaniques en longeant les côtes, où leur amplitude est bien plus importante.

Pour extraire ces informations à partir des données, on a recours à des algorithmes qui mobilisent les connaissances que l’on a, a priori, sur la physique du système étudié, et/ou à un traitement statistique des données. Dans tous les cas, cela passe par l’élaboration de programmes qui implémentent ces algorithmes — dont on en esquisse le principe ci-dessous — qui vont traiter les quantités importantes de données récoltées à l’aide de machines de calcul intensif.

Des données morcelées

Une caractéristique cruciale commune à (presque) toutes les données satellites concerne leur échantillonnage spatio-temporel, qui reflète les orbites des satellites. Ainsi, les mesures sont effectuées le long de traces, caractérisées par un temps de revisite (durée entre deux passages consécutifs en un même point) de l’ordre de la dizaine de jours. De surcroît, et particulièrement pour l’altimétrie qui mesure le long d’une ligne à l’aplomb du satellite, la couverture spatiale à l’issue de ce temps de revisite reste parcellaire : la distance entre deux traces étant typiquement de l’ordre de 300 km. Si l’on peut utiliser ces données « brutes » pour extraire des informations quantitatives sur la dynamique, toute tentative de cartographie dynamique (c’est-à-dire, d’estimation d’un champ continu en espace et en temps) implique de pouvoir estimer des valeurs aux endroits où l’on n’a pas d’observation directe, ce qui passe par l’utilisation d’un modèle au sens large.

Un premier exemple : cartographier les courants et tourbillons océaniques

Les courants et tourbillons dans l’océan ont une taille horizontale typique de l’ordre de 100 km, et évoluent relativement lentement (leur temps d’évolution est de l’ordre de la semaine). À ces échelles, un équilibre dynamique opère dans l’océan : l’équilibre géostrophique, selon lequel le gradient de pression — principalement associé, proche de la surface, aux variations du niveau de la mer — est compensé par la force de Coriolis due à la rotation du globe terrestre. Cet équilibre s’écrit : \(fv=∂_xp\),\(fu=\)\(−∂_yp\), avec :

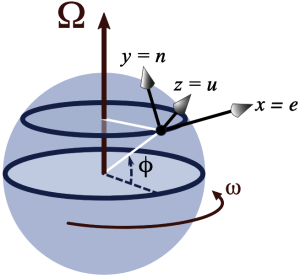
• \(f\) le paramètre de Coriolis, donné par \(f = 2Ωsinφ\) (\(Ω\) est la fréquence de rotation de la Terre, et \(φ\) la latitude du point considéré) (voir la figure 2 ci-dessous)
• \(u,v\) le courant horizontal (azimutal, méridional)
• \(p\) la pression et \(∂_xp\) dénote les variations en \(x\) de la pression (\(∂_x\) est l’opérateur mathématique de dérivation par rapport à \(x\)), similairement pour \(∂_y\). Proche de la surface, la pression est donnée par \(p≈gη\), où \(g\) est la constante de gravité et \(η\) correspond à la perturbation du niveau de la mer — c’est cette variable que l’on mesure.

On voit donc que, via la pression, les courants au voisinage de la surface sont associés à des anomalies du niveau de la mer. Ainsi, on peut estimer ces courants à partir d’une estimation des perturbations du niveau de la mer, à condition que cette estimation soit continue en espace (de sorte que l’on puisse en calculer les variations). C’est, entre autres, l’une des raisons pour lesquelles l’altimétrie satellitaire joue un rôle crucial en océanographie.

Pour produire cette estimation à partir des mesures dispersées en temps et en espace, on a par exemple recours à l’interpolation optimale. Grossièrement, cette méthode estime la valeur du niveau de la mer en chaque point, et à un instant donné, comme une combinaison linéaire des observations aux points adjacents en espace et en temps, pondérés par leur proximité en temps et en espace par rapport au point considéré. Ainsi, cet algorithme suppose que le signal estimé est corrélé en temps et en espace (c’est-à-dire, lentement variable et lisse), ce qui constitue une hypothèse de modélisation. Le résultat de cette estimation, illustré dans la figure 3 ci-dessous, nous permet d’identifier les grandes structures de courant, notamment le Gulf Stream qui se détache de la côte Est des États-Unis. En particulier, les structures annulaires correspondent à des tourbillons océaniques. On peut confronter cette estimation à des mesures in situ (qui sont plus précises mais n’offrent pas une telle couverture), ce qui donne généralement un bon accord.

Figure 3 : Ensemble des observations satellitaires du niveau de la mer recueillies durant 1 jour, le 1er février 2023 (gauche), et estimation — pour la même période — du champ d’anomalie du niveau de la mer par interpolation optimale (droite), et amplitude du courant géostrophique de surface [Ces images correspondent aux produits L3 et L4 distribués par le Copernicus Marine Service].

Un second exemple : cartographier la marée

La marée est un cas d’étude intéressant : ce mouvement étant initialement généré par l’attraction des astres (essentiellement la lune et le soleil) dont les mouvements sont réguliers et prédictibles, le signal de marée hérite de cette régularité, ce dont on peut tirer partie pour analyser les observations. En chaque point, on peut en effet formuler un modèle pour l’évolution en temps de la perturbation du niveau de la mer associé à la marée : \begin{equation}η̂(t)= \sum_{k}[a_kcos(ω_kt)+b_ksin(ω_kt)]\end{equation}. Ce modèle, qui est très étroitement lié avec la décomposition en séries de Fourier correspond à une somme de signaux harmoniques aux fréquences \(ω_k\) — typiquement, les périodes associées sont de l’ordre du jour et du demi-jour, dominant le long des côtes françaises — et d’amplitude \(a_k\) et \(b_k\). Ces dernières peuvent alors être déterminées à partir des observations, en résolvant un problème d’optimisation visant à minimiser une erreur par rapport à celles-ci. Un exemple relativement simple d’un tel algorithme d’optimisation est la méthode des moindres carrés, que l’on peut décrire comme suit. Si l’on note l’observation (pour un instant \(t_i\)) \(η^{obs}_i\), alors on définit l’erreur quadratique \(S\) comme étant : \begin{equation}S = \sum_{i}(η̂(t_i)−η^{(obs)}_i)^2,\end{equation} c’est-à-dire comme la somme des différences entre l’observation et la prédiction par le modèle, prises au carrée. L’optimisation consiste à trouver (numériquement) l’ensemble des coefficients \(a_k\) et \(b_k\) qui minimisent la valeur de \(S\). Un exemple d’estimation, et de prédiction de la marée est montré dans la figure 4 ci-dessous.

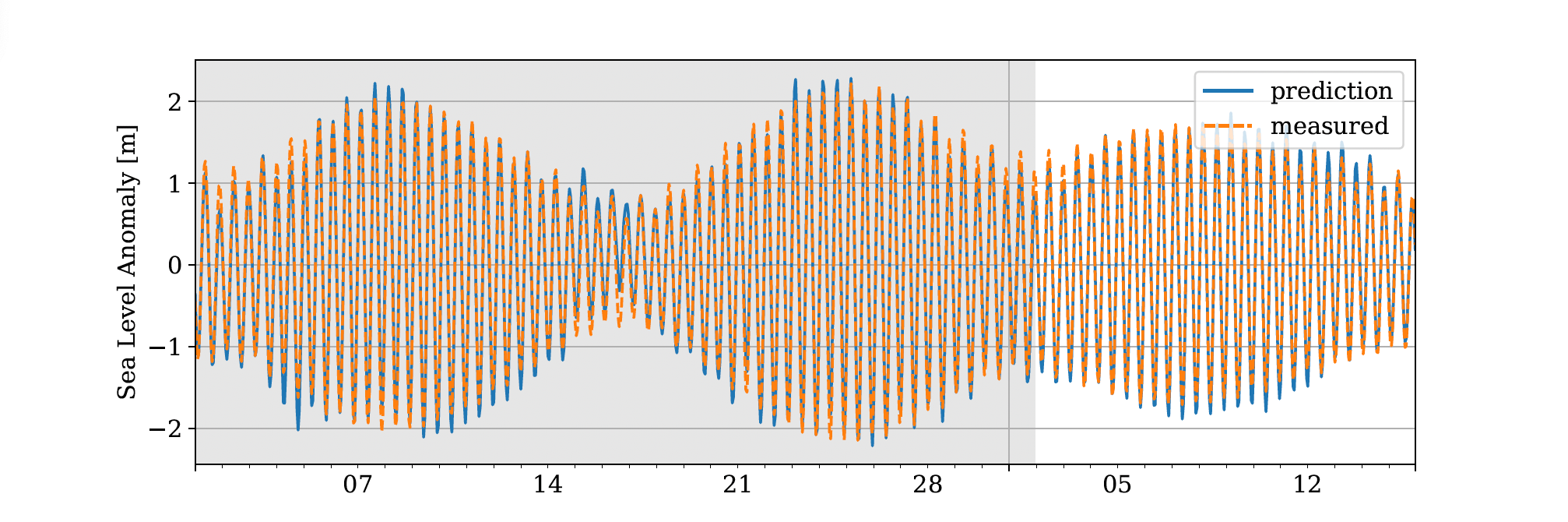
Figure 4 : Évolution du niveau de la mer pour le mois de novembre 2022 (courbe bleu) et estimation harmonique utilisant 10 fréquences de marées. Les coefficients ont été “réglés” sur la période de mars à novembre de cette année (la fin de cette période correspond à la zone grisée dans la figure). Les 15 premiers jours de décembre correspondent à une prédiction du modèle, comparée aux observations a posteriori. [Données issues d’un marégraphe à Audierne, distribuées par le portail du Service hydrographique et océanographique de la Marine, SHOM].

Conclusion

Les méthodes présentées ici ont vocation à illustrer la méthodologie derrière l’estimation de variables pertinentes à partir d’observation. Les algorithmes utilisés de manière opérationnelle sont d’un niveau de complexité supérieur à ce qui est présenté ici. En particulier, ils prennent en compte les incertitudes de modélisation et d’observation, qui sont centrales dans ces algorithmes. Néanmoins, le principe et le même : il s’agit de résoudre un problème d’optimisation sous-jacent, formulé via l’utilisation de modèles dynamiques ou statistiques, dans un contexte où les observations sont éparses. On notera que, à la différence de la prévision météorologique par exemple (cf. l’article Interstices sur le sujet), on utilise des modèles simples, ce qui est en partie dû au fait que l’on n’observe que la surface de l’océan, et qu’il est donc difficile de contraindre par les observations la dynamique sous la surface.

Les exemples traités ici montrent cependant la richesse de l’altimétrie satellitaire. Cette richesse est aujourd’hui renforcée par l’avènement d’altimètres de nouvelle génération, qui ouvrent des opportunités inédites dans le monde de l’océanographie physique. De nombreux projets cherchent aujourd’hui à améliorer ces estimations, en visant notamment une meilleure précision et une résolution plus fine, afin d’accéder à des mécanismes physiques de plus petite échelle, qui interagissent avec les structures de plus moyenne échelle dont on a discuté ici.