Internet : modéliser le trafic pour mieux le gérer
Les réseaux de communication (téléphone, Internet, réseaux locaux, etc.) ont connu au cours des dernières décennies, une expansion phénoménale. Pour leurs opérateurs, une question centrale est de savoir contrôler les flux d’information de façon optimale, afin d’éviter tout engorgement et d’offrir aux utilisateurs un service de bonne qualité, fiable et rapide. Or pour concevoir des procédures efficaces de contrôle de la circulation des informations, pour dimensionner correctement les logiciels et les équipements matériels nécessaires, une connaissance approfondie des propriétés du trafic des communications dans de tels réseaux s’impose. L’analyse mathématique du trafic dans les réseaux de communication est une discipline déjà ancienne. Elle remonte à 1917, avec les travaux engagés par l’ingénieur danois Agner K. Erlang. Sa démarche, poursuivie par beaucoup d’autres chercheurs, a fourni les principaux outils mathématiques de dimensionnement utilisés par les opérateurs et les constructeurs de réseaux, jusqu’aux années quatre-vingt-dix environ.
Jusqu’aux années quatre-vingt-dix, la modélisation du trafic par des lois statistiques classiques suffisait
Dans ses principes, la démarche mathématique explorée par Erlang et par d’autres chercheurs et ingénieurs après lui est markovienne. Cela signifie qu’elle décrit le trafic en s’appuyant sur un modèle simple de processus aléatoire, les chaînes de Markov, pour lesquelles la théorie mathématique est bien avancée et puissante (Andreï Markov (1856-1922) était un mathématicien russe qui a apporté des contributions importantes à la théorie des probabilités). En simplifiant, une chaîne de Markov est une suite d’événements aléatoires, dans laquelle la probabilité d’un événement donné ne dépend que de l’événement qui précède immédiatement. Dans le cadre des réseaux de communication, la démarche markovienne d’Erlang suppose que les lois statistiques caractérisant le trafic sont des lois de Poisson ; la loi de Poisson est une des lois de probabilité ou de statistique les plus répandues et les plus simples, elle tire son nom du mathématicien français Denis Poisson (1781-1840). L’hypothèse poissonienne s’avérait justifiée pour le trafic téléphonique (où les événements aléatoires sont les appels des abonnés et dont la durée est également aléatoire).
Ce type de modélisation du trafic a permis de mettre en place des procédures de contrôle adaptées. Jusqu’à une date récente, le contrôle des réseaux de communication était un contrôle d’admission, c’est-à-dire que l’opérateur refuse à l’utilisateur l’accès au réseau lorsque ce dernier ne peut garantir une qualité de service prédéfinie. Ce type de contrôle exige une connaissance assez précise de l’état du réseau dans son ensemble, et il n’est donc possible que pour des réseaux gérés de manière centralisée.
Mais les réseaux de communication d’aujourd’hui ne sont plus ceux d’hier. Internet a connu un développement extraordinaire ces dix dernières années. Cet essor a radicalement changé une situation qui était stable depuis plus d’un demi-siècle. Les raisons profondes de ce développement rapide résident dans l’utilisation, pour l’acheminement de l’information et le contrôle du trafic, de nouveaux protocoles de routage (IP, pour Internet Protocol) et de contrôle (TCP, pour Transmission Control Protocol) décentralisés, qui rendent le réseau Internet indéfiniment extensible.
Les propriétés statistiques du trafic ont changé, il fallait comprendre comment et pourquoi
Ces modifications structurelles ont eu des conséquences sur le trafic et ses propriétés statistiques, et il a fallu développer une théorie mathématique adaptée à la nouvelle donne. En effet, des analyses statistiques effectuées au milieu des années quatre-vingt-dix par des chercheurs de Bellcore, aux États-Unis, et de l’INRIA (Institut national de recherche en informatique et en automatique), en France, ont montré, d’abord sur des réseaux locaux puis sur le Web, que le trafic ne pouvait plus être décrit à l’aide de lois de probabilité de Poisson. Notamment, on observe des processus aléatoires à mémoire longue (où la probabilité d’un événement dépend aussi d’événements qui se sont produits relativement loin dans le passé), ce qui exclut les modélisations markoviennes classiques. Souvent, ces processus présentent également des propriétés statistiques connues sous le nom de multifractalité, qui traduisent une très grande irrégularité locale. Or toutes ces propriétés statistiques ont des conséquences importantes, par exemple pour le dimensionnement des mémoires des routeurs ; ne pas en tenir compte pourrait conduire à sous-estimer les pertes de paquets d’informations par le réseau.
Depuis les premiers articles mettant en évidence les nouvelles propriétés statistiques du trafic de données, de très nombreux travaux ont été publiés en vue de les expliquer. Aujourd’hui, on comprend assez bien l’origine du phénomène de mémoire longue constaté dans la statistique du trafic. On a pu établir qu’il découle directement de la répartition statistique des tailles de fichiers contenus dans les serveurs web, ainsi que des tailles des fichiers demandés par les utilisateurs lors des requêtes HTTP (protocole de transfert hypertexte, utilisé lorsqu’on surfe sur le web) et FTP (protocole de transfert de fichiers). Leurs courbes statistiques, c’est-à-dire les courbes représentant le nombre de fichiers échangés ou consultés en fonction de la taille, décroissent, pour les grandes valeurs, moins rapidement qu’une exponentielle : on dit que leur loi de probabilité est « à queue lourde ». Ce que l’on a montré, c’est qu’en représentant le comportement individuel des internautes par un modèle probabiliste simple fondé sur ces lois statistiques à queue lourde, et en superposant le trafic d’un grand nombre d’internautes ainsi modélisés, on obtenait bien le phénomène de mémoire longue caractérisant le trafic global.
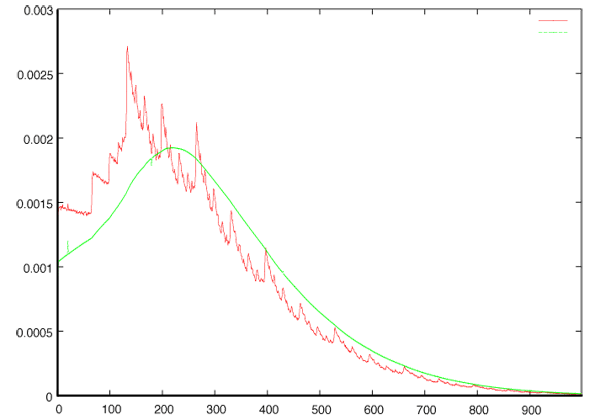
Loi du débit obtenu par une source HTTP (simulation Netscale).
En rouge : la loi du débit aux instants de congestion. En vert : la loi du débit en temps continu.
Analyser le protocole TCP et ses effets afin d’améliorer la gestion du réseau Internet
Tout n’est pas éclairci pour autant. Les travaux actuels se concentrent sur l’explication des propriétés statistiques du trafic aux petites échelles de temps, la multifractalité en particulier. L’hypothèse la plus répandue est que cette propriété résulte des protocoles de contrôle utilisés, et notamment de TCP. Mais en quoi consiste le protocole TCP, qui contrôle actuellement près de 90 % du trafic sur Internet ? Il s’agit d’un contrôle de flux adaptatif, où le débit d’information émise par une source est commandé par un algorithme qui augmente linéairement le débit d’émission au cours du temps, tant qu’il ne se produit pas d’engorgement ; mais dès que des pertes sont détectées, l’algorithme réduit de moitié le débit d’émission.
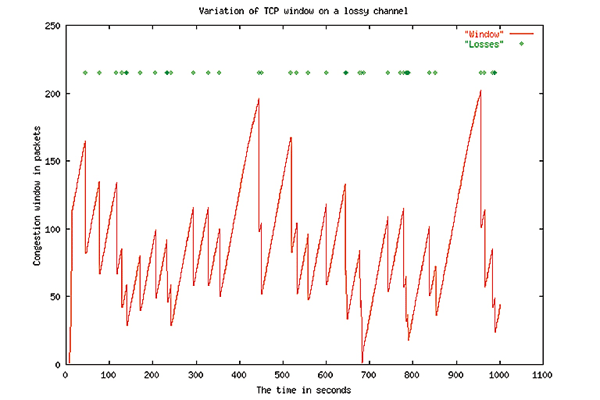
Simulation de comportement de contrôle de congestion TCP/IP en présence de pertes aléatoires.
En rouge : le débit instantané. En vert : les pertes aléatoires sur le canal.
C’est ce contrôle adaptatif qui règle toute réponse à la congestion dans le réseau. Son analyse mathématique présente de nombreuses difficultés, en raison du caractère décentralisé, stochastique (l’encombrement et les pertes évoluent aléatoirement), non linéaire (les effets ne sont pas simplement proportionnels aux causes), complexe (réseau très étendu, impliquant des interactions entre nombreux routeurs intermédiaires) de la situation. Or l’élaboration de modèles intégrant tous ces éléments est un enjeu majeur, qu’il s’agisse de définir des règles de dimensionnement du réseau, d’optimiser les débits ou de prédire et contrôler les variations aléatoires de la qualité de service offert par le réseau à ses utilisateurs.
Des défis scientifiques et des enjeux économiques, qui mobilisent les universitaires et les industriels
Une telle tâche exige des efforts de recherche dans des domaines très divers (statistiques, théorie des probabilités et des files d’attente, contrôle adaptatif de systèmes non linéaires, théorie des grands réseaux stochastiques, systèmes dynamiques) et qui dépassent ceux de l’approche traditionnelle. Ces dernières années, un grand nombre de modèles plus ou moins simplifiés ont ainsi été proposés. Certains d’entre eux permettent de rendre compte de la multifractalité du trafic global, propriété évoquée plus haut, d’autres permettent d’évaluer si le partage d’un même canal de communication entre plusieurs flux de données contrôlées par TCP est équitable, etc.
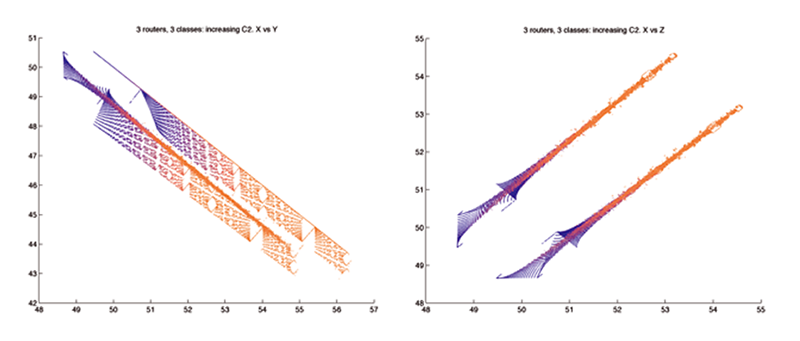
 |
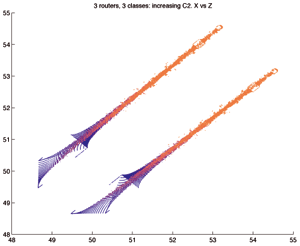 |
| Fractales obtenues dans l’étude d’un système dynamique représentant le partage de bande passante opéré par TCP. | |
Les recherches actuelles se concentrent aussi beaucoup sur l’analyse de DiffServ, une méthode de différenciation des services offerts, fondée sur la création de classes de priorité pour les échanges de données. Cela paraît être la seule démarche extensible capable d’améliorer la qualité de service dans le réseau Internet. Un autre axe important concerne l’adaptation d’UDP (User Datagram Protocol), un protocole utilisé pour les flux de données vidéo et vocales, flux qui ne sont pas régulés par TCP, notamment dans le but de définir des modes de transmission de ces flux qui soient compatibles avec TCP.
Une autre direction de recherche importante concerne la définition de réseaux applicatifs extensibles et n’utilisant pas d’autres protocoles de routage et de transport entre deux points que ceux de l’Internet actuel. Les réseaux pair à pair, les réseaux de diffusion de données ou de recherche d’informations disséminées sont des exemples typiques de tels réseaux applicatifs. Ces réseaux sont extensibles si les mécanismes d’organisation et de contrôle qui les sous-tendent sont décentralisés et fonctionnent de manière satisfaisante lorsque le nombre d’utilisateurs est très grand.
Face à ces questions qui présentent des défis scientifiques et des enjeux économiques de première importance, le monde académique et le monde industriel s’organisent. Comment ? La plupart des grands groupes industriels des technologies de l’information et des opérateurs ont constitué des équipes de haut niveau, centrées sur la modélisation du trafic et du contrôle dans les réseaux de données, et tout particulièrement dans le réseau Internet, tant au niveau du cœur du réseau qu’à celui des réseaux d’accès qui prennent aujourd’hui des formes très diverses : accès DSL (Digital Subscriber Line), accès sans fil 3G ou Wifi, etc. L’effort du monde académique n’est pas moindre, notamment aux États-Unis, en Europe et dans certains pays asiatiques, où se mettent en place des collaborations interdisciplinaires entre des mathématiciens et des chercheurs en informatique en en génie électrique.
L’instance qui a la plus grande influence dans l’évolution du réseau Internet est sans doute l’IETF (Internet Engineering Task Force). Elle est ouverte à chacun, qu’il soit concepteur de réseau, chercheur ou opérateur. Les activités se déroulent sous forme de groupes de travail portant sur plusieurs domaines tels que le routage, la sécurité, le transport, le contrôle de congestion, les applications, etc. Ces groupes de travail sont chargés de faire des recommandations dont certaines deviendront des normes. La validation de ces recommandations par des études mathématiques, du type de celles évoquées dans cet article, constitue une composante importante et parfois décisive du travail de normalisation.
- R. Riedi et J. Levy-Vehel, « Fractional brownian motion and data traffic modeling : the other end of the spectrum », Fractals in Engineering (Springer-Verlag, 1997)
- M. Taqqu, W. Willinger et R. Sherman, « Proof of a fundamental result in self similar traffic modeling », Computer Communication Review, 27, pp. 5-23 (1997)
- F. P. Kelly, A. K. Maulloo et D. K. H. Tan, « Rate control in communication networks : shadow prices, proportional fairness and stability », Journal of the Operational Research Society, 49, pp. 237-252 (1998)
- K. Park et W. Willinger (Eds), Self similar traffic analysis and performance evaluation (Wiley, 2000)
- P. Abry, P. Flandrin, M. S. Taqqu et D. Veitch, « Wavelet for the analysis, estimation and synthesis of scaling data », dans la référence ci-dessus
- S. Low, A Duality Model of TCP and Queue Management Algorithms, IEEE/ACM Transactions on Networking (TON) Volume 11, No 4, août 2003.
- F. Baccelli, A. Chaintreau, Z. Liu et A. Riabov, « The One to Many TCP Overlay », Actes d’IEEE INFOCOM’05, Miami, mars 2005.
- F. Baccelli et D. Hong, Interaction of TCP flows as billiards, IEEE/ACM Transactions on Networking (TON) Volume 13, No 4, août 2005.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

François Baccelli